A Particle Swarm Optimization Approach for Energy Efficient Clustering in Wireless Sensor Networks

Published Online June 2017 in MECS

Recent advancement in embedded and wireless technologies allows the micro autonomous system comprised of small tiny devices known as sensors. These sensors can detect, compute and communicate via suitable sensor technology that gives birth to wireless sensor network. Deployment ease and low cost sensors make wireless sensor network suitable for many applications like: health care, transportation, smart building, and environmental monitoring etc [1-3]. Though, the most important constraint of WSNs is the restricted power supply of nodes. Therefore, the energy saving of nodes is most demanding problem for long run network operations. Several issues have been studied that include wireless radio hardware, energy efficient MAC protocols etc [4,5]. But, efficient clustering and routing schemes are the very much promising fields that have been studied comprehensively in this regard [5-7].

In two-tier WSN, nodes are separated into some sets termed clusters. Each cluster has a leader node recognized as a cluster head (CH). Every node senses topical data also forward it to relevant CH. Subsequently, CH aggregates that data and sends it to base station (BS) straightforwardly or via further CHs. A clustered WSN is revealed in Fig. 1.

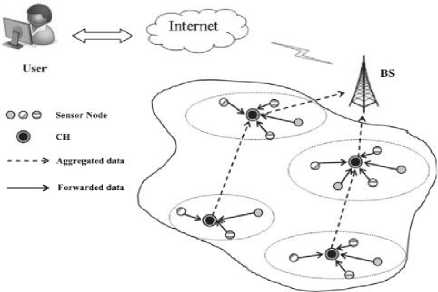
Fig.1. A clustered wireless sensor network ([28])

Clustering sensor nodes has the following benefits: (1) It facilitates aggregation of data at CH to get rid of the superfluous and un-correlated data; thus it saves power of nodes (2) Routing can be much simply maintained as only cluster heads have to manage the local routes set up of another CHs and therefore need little routing info; this sequentially advances the network’s scalability (3) It too preserves transmission bandwidth because nodes be in touch with just relevant CHs and therefore keep away from switch over of redundant communications amongst themselves. Though, CHs bear some extra load contributed by their member nodes as they receives the sensed data from their members, aggregate that and communicate it to sink node. Furthermore, in several sensor networks, the CHs are generally chosen among the normal nodes that can die rapidly for such additional load. In this perspective, lots of researchers have recommended to bring into play of few extraordinary nodes termed as heads, which are furnished with added energy

• [23,26,27,31].    These nodes acts like leaders of cluster and are accountable for the similar practicality of the CHs. Hence, CHs and heads are used interchangeably in the remainder of this paper. Unluckily, heads are also battery regulated and therefore power restrained. Lifetime of heads is extremely essential for long run function of the system. It is noteworthy that transmission energy (E) which mostly dominates the overall energy utilization is directly proportional to the distance (d) among transmitter and receiver i.e. E α d^β where β is the path loss coefficient and 2≤β≤4 [27]. Therefore minimization of transmission distance can decrease the energy expenditure. Though, a few applications are extremely time critical in nature. Thus, they must satisfy strict delay restrictions so that the BS can get the sensed data within a specified time bound. But delay is directly proportional to quantity of forwards on the dissemination route from source to sink. So, as to minimize the delay, it is essential to reduce the quantity of forwards, it can be attained via maximizing the distance among successive forwards. Therefore, while designing routing we need to incorporate a trade-off among communication distance and amount of forwards as they pose two conflicting goals. Furthermore, load balancing is another key issue for WSN clustering. Mainly, this is vital concern when the nodes are not dispersed evenly. In this work, we concentrate on the following issue: Energy efficient clustering with energy conservation of the sensor network.

Let us consider that there are n nodes as well as m heads; the no. of probable clusters is mn. It should be noted that if the heads contain an average of d legitimate single-hop nearby relay nodes, in that case the quantity of applicable paths is dm. Hence, the computational complexity of discovering the optimal route and cluster for a big network looks to be extremely high via brute force scheme. Moreover, an optimization method requires reasonable amount of memory and computational resources and yet finding out good results is desirable. In order to obtain quicker and competent solution of clustering problems with above concerns, meta-heuristic scheme for example particle swarm optimization is very much enviable. The key idea of this work is to develop a competent PSO-based clustering algorithm for WSNs with the concern of energy utilization of nodes for prolonging network lifetime.

The main contribution of authors in this work is illustrated as: In this paper, first non-linear programming (NLP) formation is presented for the clustering issue. Then PSO-based algorithm for the clustering problem is proposed. In fact proposed PSO-based clustering minds the energy expenditure of normal nodes as well as the head nodes. To clustering, particles are skillfully encoded to make absolute clustering way out. A dissimilar fitness function is too exercised with the concern of those heads which unavoidably uses more energy by performing like relay node in message forwarding. We carry out wide simulation on proposed method as well as assess that with some performance metrics containing no of alive nodes, energy consumption, packet delivery ratio etc. So, our main contribution is summarized as:

• •    NLP formulation for clustering problem

• •    PSO-based clustering algorithm with competent

particle encoding method and fitness function

• •    The simulation of proposed algorithm to reveal the superiority over some existing ones.

The remainder of this paper is planned like so. The related work is expressed in section II.  The outline of particle swarm optimization is explained in section III. Then model used by our protocol is explained in section IV. The proposed algorithm is expressed in section V. The simulation results are illustrated in section VI. At last, section VII concludes the work.

• II.    Related Work

  Various clustering and routing schemes for WSNs have been reported in literature [8-10]. We present the review of similar work on the basis of heuristic and metaheuristic techniques. Though, we focused on metaheuristic approach as our proposed algorithm is derived from it. In [26], Low et al. have designed a clustering method by considering a BFS node tree to discover the slightest loaded head for allocating a node to a CH. The computational complexity of the method is O(mn²) where n nodes with m cluster heads. For large scale networks, it looks like that run time of algorithm is extremely high. In [19], Kuila and Jana suggested a load balanced scheme that run in O(nlongn) which is an enhancement over Low et al. model. Many heuristics have been proposed for routing in WSN. LEACH is a famous hierarchical routing protocol that vigorously rotates the loads of CHs amid the nodes that is helpful for load balancing [11]. Though, the most important weakness of such scheme is that a low energy node possibly elected as cluster head which can die rapidly. Furthermore, the CHs converse with BS via one-hop that is unrealistic for WSN with immense coverage region. As a result, lots of schemes have been designed toward the improvement in LEACH [12-16]. In [13], O. Younis proposed the hybrid energy efficient distributed clustering schemes (HEED) for ad-hoc wireless networks. The HEED periodically chooses the CHs on the basis of node’s remaining energy and connectivity measure of nearest node or node degree. Several meta-heuristic based clustering schemes have been revealed for sensor networks. However, most of them have dealt with CH selection only. Furthermore, the algorithm that doesn’t consider left over energy of nodes and heads in cluster construction which may direct to imbalance expenditure of the node’s energy. In [29], Gupta et al. designed a genetic algorithm based routing method (GAR) where on the whole transmission distance between the heads and BS is minimized. Though, this algorithm considers simply routing of cumulative data from the heads to the sink with no consideration of data transmission from the nodes to the heads inside a cluster. In [30], Chakraborty et al. proposed a routing scheme on the basis of differential evolution for over 1000 relay nodes in a way that the power expenses of the most energy intense relay node is curtailed. But, the instigators

don’t mind regarding the cluster construction. Various inappropriate clustering may cause severe energy inadequacy of the relay sensors. In [24], Singh and Lobiyal utilized the PSO for cluster head election amongst the member nodes and don’t mind the cluster configuration. The PSO and ACO are employed in sensor networks for added optimization problems as well. Various optimization based energy efficient schemes have been reported in literature [20-22, 25]. Though, no one of the above algorithms think about the overhead of the data routing in cluster construction phase. In [23], Kuila et al. focuses on cluster creation with nature-inspired technique. Numerous works were suggested for the CH selection. However, choice of the CHs simply can’t shape the clusters. To the best of our knowledge, there is no bio-inspired clustering algorithm such as PSO based which considers cluster formation rather than CH selection for WSNs.

• III.    Particle Swarm Optimization

Particle swarm optimization (PSO) is inspired by natural existence, like bird flocking, fish schooling [17,18]. It can be noticed from the nature that animals, particularly birds, fishes, etc. at all times travel in a group with no collision. It is because every member pursues the group by altering its position and velocity by the group info. Therefore, it eases individual's effort of looking for the food, shelter etc. The various steps of a PSO are described in the flow sheet as revealed in Fig. 2.

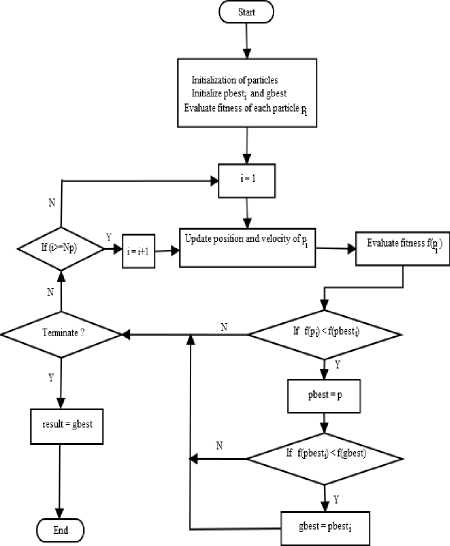
Fig.2. Flow chart of PSO

PSO be composed of a swarm of a pre-defined particle amount (N P ). Every particle provides a comprehensive explanation to the multi-dimensional optimization issue. The dimension D of every particle is identical. A particle

Pi, 1 ≤ i ≤N P has position X id , 1 ≤ d ≤ D in addition to velocity V id in the d^th dimension of the hyperspace. We take up the notation for depicting the i^th particle P i of the population as follows:

P i = [ X i,1 , X i,2 , …….. X i,D ]

Each particle is assessed through a fitness function to examine the merit of the solution for the problem. To make up to the global best position, P i tracks its individual best, that is personal best labeled pbest_i along with global best labeled gbest for updations of its velocity and position. In every iteration, velocity V id as well as position X id is updated with the equations given as:

V id ( t ) = ® ^x V id ( t - 1) + c l ^x r l ^x ( Xpbest dl ^- X id ( t - 1 ) ) + c 2 ^{x r} 2 ^X ( Xgbest^ - X d ( t - 1 ) )

X d ( t ) = X d ( t - 1 ) + V d ( t )          (2)

Where ω denotes the inertia weight, c 1, c 2 are acceleration factors and r 1, r 2 are two dissimilar random numerals between 0 & 1. The method of updation is iteratively repeated till the adequate gbest is reached or the fixed quantity of iterations t max is attained.

• IV.    System Model

Here, we illustrate the network model and radio energy model used in proposed method.

• A.    Network model

Let us consider a network model alike to that utilized in LEACH with the following characteristics:

• 1)    Every node carry out sensing tasks sporadically and all the time send data to BS.

• 2)    A fixed BS can be placed inside or outside the network area.

• 3)    The entire nodes are fixed and energy restrained.

• 4)    Each and every node is capable of working in CH mode as well as in sensing manner.

• 5)    Data fusion is utilized to lessen the overall data.

• B.    Energy model

In this work, we employ an energy model of radio (REM) as shown in Fig. 3.

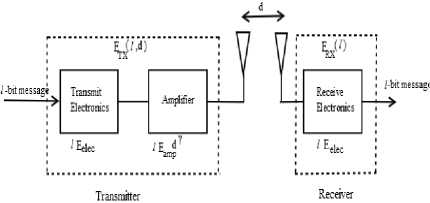
Fig.3. Radio energy model

In REM, transmitter depletes energy to operate radio as well as power amplifier, moreover the receiver uses up the energy to operate radio [27]. The radios can carry out the power control and thus utilize minimum energy needed to get to the destined recipients. Because of attenuation, energy loss model is applied for small and long distances. Hence, to realize signal-to-noise ratio (SNR) during broadcasting l -bit packet over distance d , the energy dissipated by radio is specified as:

in addition to minimize the energy expenditure of the nodes. By the network lifetime, we denote the time as of the WSN deployment till the death of the very first head. Hence, life of network can be maximized if we can maximize the minimum lifetime of the heads. Energy expenditure of the nodes can be minimized through the minimization of the distance among nodes and their corresponding heads. Let b ij be a Boolean variable expressed as:

E TX ⁽ l , d ) =

lE elec

<

lE elec

+ lefsd 2,

^{+ e>}mp^w ,

if ^d 5 d 0 if d >  d 0

b

1 if sis assigned to clsuter head h, , V i , j :1 <  i <  n ,1 <  j <  m 0            otherwise

Wherever, E elec represents energy depleted per bit to operate the electronic circuitry, ε fs and ε mp depends on amp model, d denotes the distance among sender and receiver, and d₀ is the threshold transmission distance.

The threshold distance d 0 is given by:

Equating the equation (3) for d = d 0

lE elec ^{+ l e} fs d 0 = ^lEelec ^{+ l e} mp^d 0

Let L be the minimum lifetime of CHs and AvgDst be the average distance among sensor nodes and their related CH.

L = min{ L ( h j ) | V j ,1 <  j <  m}            (6)

Where L(h j ) denotes the lifetime of head h j and given as:

d

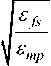
^L ( h ) =

E , Ah \ residual j

Econsump ⁽ hj )

To obtain l- bit message, the radio uses:

E RX ( l ) = l . E elec                    (4)

• V. Proposed Work

Network setup is completed in three stages: bootstrapping, route setup, clustering. During bootstrapping procedure, the entire nodes and heads are allotted unique IDs. Subsequently, the nodes as well as the heads broadcast their identifiers with CSMA/CA MAC protocol. Thus, the heads can gather the identifiers (IDs) of the nodes as well as the other heads those are inside their communication range and eventually propel the local network info to the sink. Now, using the received information of the network, BS performs the routing and clustering algorithm. Note that after execution of the routing algorithm, the base station uses the final route setup for proper formation of the cluster. As the routing and clustering is ended, the entire heads are updated regarding their next hop relay node to the sink and the nodes are furthermore notified on the subject of the ID of the heads they belong to. Then the heads give a TDMA plan to their members for intra cluster communication. The heads use slotted CSMA/CA MAC scheme to be in touch with its next hop relay node. Now, we express our proposed clustering schemes as follows.

• A.    NLP formulation of clustering problem

Now, we concentrate on the clustering problem where our basic objective is to maximize the lifetime of network

Where h j has residual energy E_residual ( h j ) and energy consumption per round is E_consump ( h j ) .

Our objective is to extend network lifespan by allotting less no. of nodes to the CHs with lesser lifetime. Thus, we make the subsequent formulation:

Maximize Y = min{L(hj) | Vj,1 < j < m(8)

And nm

AvgDst = - ^^d(si, hj) x by(9)

ⁿ i = 1 j = 1

After that the non linear programming of the clustering issue is formulated as:

Maximize Z = (10)

AvgDst

Subject to

m

^Ьу = 1,1 <  i <  n j = 1

m

^d (si, hj ) x bij < CRmax,1 < i < n, si- e 5, hj e H j=1

Where S and H are group of sensors and CHs respectively and CR max is the maximum communication range of CH.

The above constraints affirm that sensor nodes can be allocated to one and only one head and within its communication range.

• B.    Proposed clustering algorithm

The base station implements the clustering algorithm in which the information of routing solution is used for the cluster formation to balance the load of the CHs. Note that we use here particle initialization for clustering and formulation of fitness function.

• 1)    Initialization of particles

Here, the particle dimension is identical to the quantity of nodes (i.e., n) inside the system. Let, P i = [X i,1 , X i,2 , X i,3 , …, X i,n ] is the i^th particle in the population wherever every element, X i,d , 1 ≤ i ≤ N P , 1 ≤ d ≤ n interprets the allotment of the node s d to a head. We initialize every element by a randomly created evenly dispersed number Rand (0,1], 0 ≤ Rand(0,1] ≤1. This number is created autonomously for every element in random fashion. The element of the d^th dimension of this particle, i.e., X i,d =Rand(0,1], 1 ≤d ≤n maps a head (say g k ) to which the node s d is allotted.

The mapping is complete as:

• h k = Index ( CrangeCH ( s_d ) , n ) (11)

Where Index(CrangeCH(s d ),n) is an indexing function that indexes the n^th CH from CrangeCH(s_d) and n= Ceiling( X_i,d×| CrangeCH(s_d)|). CrangeCH(s_d) is the group of the entire CHs those are in the transmission range of the node s d and expressed as:

CrangeCH ( ^s _d ) = { h j | d ( s d , h j ) <  Rs_d p h e H } ⁽¹²⁾

It is significant to note down that the particle illustration expressed above is a piece of clustering method. As stated above, the dimension of every particle is the identical to the amount of nodes. Thus, addition/deletion of a node would alter the particle dimension in addition to the need of reclustering.

Example: Let us study a WSN that have 12 nodes along with 5 heads i.e. S= {s 1 , s 2 , …..s 12 } and H= {h₁, h₂,……h₅} as shown in figure 4. The dimension of particle is equal to the amount of nodes, i.e., n=12. The edges among nodes and CHs specify that the CHs are in the range of the nodes. It can be examined from Fig. 4, that sensor node s3 is connected with two heads. Table 1 shows the sensor nodes and the heads within its communication range. Currently, for every element of the ith particle at p^th generation, a digit is created randomly to initialize the component. Consider that the randomly created number for third element is 0.89.i.e. X_i,3=0.89. Hence, Ceiling (X i,3 x |CrangeCH(s 3 )|)=3, therefore third head from CrangeCH(s 3 ), i.e.h 5 is selected for assigning s 3 as shown in Fig. 5. Therefore, the particle

P i =[0.28,0.81,0.89,0.16,0.72,0.10,0.42,0.60,0.26,0.51,0.7 0,0.42] maps to the assignments of the nodes to their CHs as shown in Fig. 4.

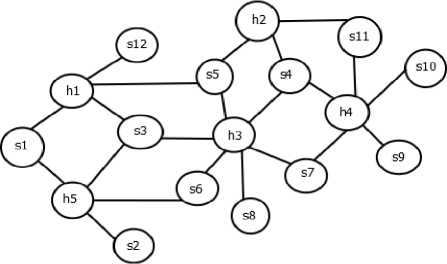
Fig.4. A WSN with sensor nodes and head nodes

Table 1. Sensor nodes with directory of probable CHs

Sensor node	CrangeCH(s d )	|CrangeCH(s d )|
s 1	{h 1 ,h 5 }	2
s 2	{h 5 }	1
s 3	{h 1 ,h 3 ,h 5 }	3
s 4	{h 2 ,h 3 ,h 4 }	3
s 5	{h 1 ,h 2 ,h 3 }	3
s 6	{h 3 ,h 5 }	2
s 7	{h 3 ,h 4 }	2
s 8	{h 3 }	1
s 9	{h 4 }	1
s 10	{h 4 }	1
s 11	{h 2 ,h 4 }	2
s 12	{h 1 }	1

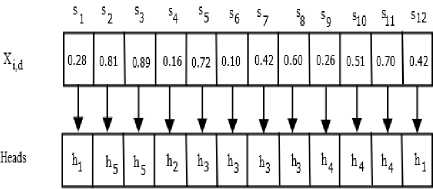
Fig.5. Next-hop cluster head selection from random particles

• 2)    Initialization of particles

The fitness function is derived in such a way that it pays attention to the energy utilization of the cluster heads and the nodes. The derivations depend on some parameters described as follows:

• a)    Lifetime of CHs

For maximizing the network lifetime, we have to maximize the lifetime of CH that has the least lifetime. The general idea behind the maximization of CH life is that the CH with lesser remaining energy ought to have lesser rate of energy expenditure for every round than the CH with greater remaining energy. Hence, the lifetime of CH with lesser residual energy can be prolonged effectively. The CHs consumes their energy for receiving sensed data from their constituent nodes, do data aggregation and lastly forward that data to the sink. So, the energy expenditure is basically in intra-cluster activity and inter-cluster movement.

The energy utilization by head node h j in intra-cluster activity is expressed as:

E intra - cluster ( h j ) = A ( h j )| X ( E r + E )       (13)

Where |A_s(h j )| is the quantity of nodes in the cluster transmission range of CH h j . E_R and E_DA represent the energy consumption in receiving the packets and aggregating the packets. Total energy consumption by head node h j is given as:

E consump ⁽ h j )    Eintra - cluster ⁽ h j ) ⁺ E inter - cluster ⁽ h j )    ⁽¹⁴⁾

Let residual energy of h j is E residual ( h j ) . Then the lifetime of h j can be calculated as:

L ( h ) =

E Ah )

residual j

E consump ⁽ h j )

Our first objective is to maximize the least lifetime of CH is expressed as:

Maximize L = min{ L ( h j ) | V j ,1 <  j <  m }     (15)

Fitness ^ L                 (16)

• b)    Average distance of cluster

To maximize the lifetime of CHs, a few nodes are forced to be assigned to head node which is farther from it. Thus the sensor nodes consume their energy faster and die quickly due to long distance communication with their head node. So as to minimize the energy utilization, nodes should be allocated to their nearest CH. Thus, we measured the average distance among sensor nodes and their related CH. So, our second objective is to minimize this distance.

1 ⁿ

Minimize AvgDst =   E d ( s i ^, h i )

i = 1

Where h i is the head node of sensor s i . The lesser the AvgDst, the greater is the fitness value. Thus, fitness function is reciprocally proportional to AvgDst.

Fitness «---1 (18)

AvgDst

By merging above fitness relations (equation16 and equation 18), we get the fitness as:

Fitness « —-—(19)

AvgDst i.e.

Fitness = C x —L—

AvgDst

Where, C denotes proportionality constant. The fitness value is utilized for evaluation so the value of C doesn’t influence our objective. So, let us consider C=1. The fitness is expressed as:

Fitness = —-—           (21)

AvgDst

The higher the fitness value, the better is the particle position. Thus, our overall objective is to maximize the fitness function.

The flow sheet of proposed method is revealed in Fig. 6.

Fig.6. Flow sheet of proposed method

• VI.    Simulation Results

The performance analysis of proposed algorithm is done with help of NS-2.35. In the network, 100 nodes are organized in random fashion in 100m×100m area where BS is situated in network region. The performance assessment of proposed work is done as per the certain parameters given as:

Energy consumption : total energy consumed by all the nodes in their intra-cluster and inter- cluster activities

No. of alive nodes: quantity of nodes that have not so far exhausted their power

Packet delivery ratio: ratio of actual packet delivered to total packet sent

End-to-End delay:   time taken for packet to be communicated across a network from source to destination

Throughput: number of packets per bytes received by source per unit time

The proposed algorithm is evaluated with LEACH, HEED, in term of alive nodes over rounds, Packet delivery ratio, energy expenditure, end-to-end delay, and throughput. The complete amount of rounds exercised in experiment is 500. The network parameters utilized in simulation are outlined in Table 2.The PSO specifications are revealed in Table 3.

Table 2. Network parameters

Parameter	Value
Nodes	100
Network size	100m×100m
BS location	(50,75)
Initial node energy	2 J
E elec	5 nJ/bit
E TX =E RX	50 nJ/bit
ε fs	10 pJ/bits/m2
ε mp	0.0013 pJ/bits/m4
E DA	5 nJ/bit
Packet size	500 bytes
No. of CHs	5
No. of rounds	500

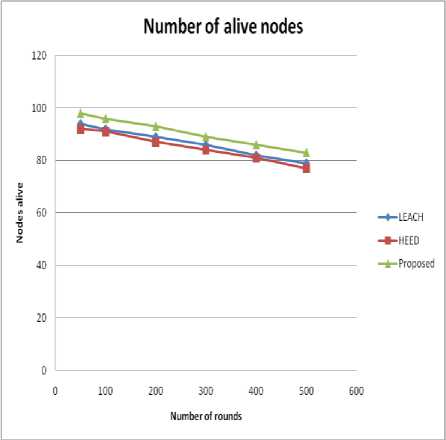
Fig.8. Number of nodes alives over rounds

Table 3. PSO parameters

Parameter	Value
Particle size (Np)	30
Number of Iterations	20
ω	0.9
c 1 , c 2	2.05, 2.05
max ,    min	0.4, -0.4

Fig. 7 demonstrates the comparative analysis of energy consumption of the proposed method with LEACH and HEED. It is clear that proposed algorithm have better energy usage as compared to LEACH and HEED.

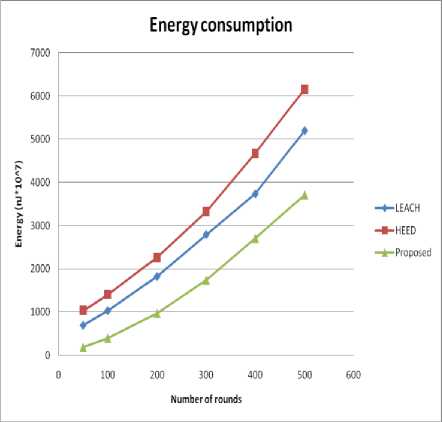
Fig.7. Energy consumption over rounds

Fig. 9 and Fig. 10 illustrate the PDR and End-to- End delay over rounds in the network respectively.

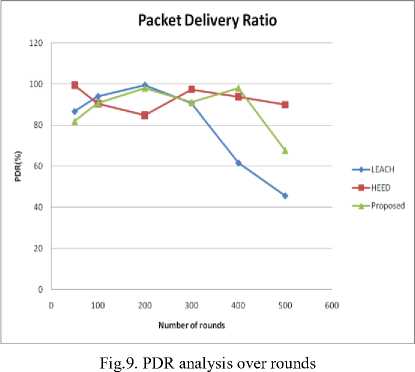
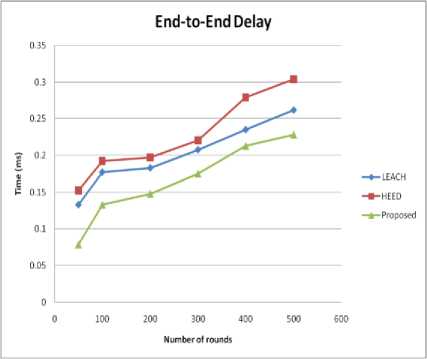
Fig.10. End-to-End Delay over rounds

Fig. 8 shows the number of nodes alive per round demonstrating stability of the network.

Fig. 11 illustrates the throughput demonstrating the efficiency of the network.

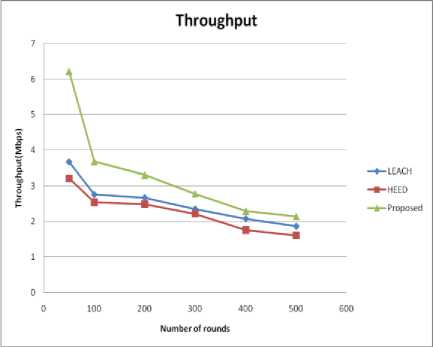
Fig.11. Throughput over rounds

• VII.    Conclusion

In this paper, the non linear programming formation for clustering problem in WSN is described. Then an energy efficient clustering scheme for WSN with PSO approach is presented. In the presented algorithm, the energy consumption of CHs is significantly balanced to improve the network lifetime. The presented algorithm is based on derivation of efficient particle encoding method and fitness function derivation. We have carried out thorough simulation. Furthermore, the results are evaluated with existing algorithms namely LEACH, HEED. Simulation results clearly states that proposed algorithm excels the existing algorithms.

Acknowledgement

This work is carried out with the help of human resource development ministry (MHRD) under research grant in support of doctoral study.