A regularized Levenberg-Marquardt type method applied to the structural inverse gravity problem in a multilayer medium and its parallel realization

This paper is concerned with iterative solutions solving the inverse structural gravity problem in a multilayer medium and is a continuation of the series of works [1, 2].

Hence we consider an operator equation

A ( u ) = f,                                          (1)

where A(u) is nonlinear Frechet differentiable integral Urysohn type operator between Hilbert spaces U,F , u = ( u o ,.., u l ) are unknown functons describing L desired interfaces, f is the total gravitational field. The solution of (1) does not depend continuously on the data and thus using of noise-contaminated data would lead to a meaningful deviation from solution. Hence a stable

^\ast The paper is recommended for publication by the Program Committee of the International Scientific Conference “Parallel Computational Technologies (PCT) 2017”.

solution of (1) requires regularization techniques, for example the method of Tikhonov. We obtain

A ' ( u ) * ( A ( u ) - f _s )+ a(u - u ⁰ ) = 0 ,                             (2)

where A ' ( u ) * is a conjugated operator for derivative operator A ' ( u ), a >  0 is a regularization parameter, \| f - f _\delta \| \leq \delta , u ⁰ is an initial approximation. So we will assume solving equation (2). To solve (2) the regularized Levenberg–Marquardt algorithm can be used [3]:

u k +1 = u k - ₇ [A(u k ) * A ' ( u ^k ) + al ] ^{- 1} [ A ^z ( u ^k ) * ( A ( u ^k ) - f _s ) + a(u - u ⁰ )]          (3)

where \gamma is the damping factor. This method used in iterative solution nonlinear inverse problems of filtration, borehole and exploration geophysics ( [3–5]) etc. In the article [6] the method (3) strong convergence to the solution is set up for the Tikhonov-regularized equation on the assumption that the condition of the sourcewise representability of the solution z of the equation (1) and the Lipschitz conditions for the derivative of the operator A are fulfilled and the initial approximation is taken from a rather small neighborhood of the regularized solution.

l|A'(u)ll< Ni,   ||A'(u) - A'(v)b< N2^u - vb, z - e = A'(z)4  hvh < 1/N2.

This method is complex to implement. It takes a lot of time for matrix to matrix multiplication, matrix inversion. It is possible to use iterative methods for matrix inversion, so the iterative process is two-step: at each step we reduce the problem to SLAE, which we solve by some iterative method. We can see that LM algorithm tends to have larger computational overheads with an increase in the size of input data.

The previous work [2] is concerned with a regularized Levenberg–Marquardt method (CLM) which within the weight factors approach proposed in [7] lets find simultaneously several structural boundaries described by unknown functions u 0 , .., u L in equation (1) using the total gravitational field f . Weight factors w i will be chosen as follows:

F = ^[ F 1 , F 2 , •••, F L ^] = ^(f 1 ^,f 2 , •••, ^f M x L , •••, ^f L x M x N )

^ ( w i , W 2 , •••,W L x M x N ) ,

W i =     ' ■ , ^ >  1 ,                                         (4)

max I f i | P

i where Fi(l = 1, 2, •••,L) are anomalous fields generated by the gravitating mass located below the corresponding depths Hi for the sought surfaces of interface Si(l = 1, 2, •••, L). Weight factors depend on field Fl which separated from field original F using preliminary processing of gravity observations [8].

Linearized gradient type methods based on linearized steepest descent method with weight factors (5) for solving the gravity problem are considered in works [9, 10]

k+1     k ,       hS(uk)h2    k,kx ui    = ui   ^Wi hA'(uk)s(uk)h2Si(u ),                             (5)

where S ( u ^k ) = A ' ( u ^k ) * ( A ( u ^k ) - f ), \psi is damping factor. This method is suited to deal with multilayer problem but there is a matrix to matrix multiplication operation.

Also in [11] a Levenberg–Marquardt gradient method based on Landweber-type scheme is proposed k+1= k       (Ai[uk] - Fi) dAi[uk] 1

u i       u i ^ |V A i[ u ^k ]|| ² ЭЦ ?    •

As seen, this method is fast but is suitable only for finding interfaces in two layer model.

The present paper is focused on comparison of relative errors, numbers of iterations and computation times between classic regularized Levenberg–Marquardt method (LM) and CLM. Here there are used gravitational field models with uniform 15% noise. In a view of big memory consumption and high computational complexity of LM some algorithmic optimizations are proposed. On a basis of algorithms the parallel programs are implemented using OpenMP and CUDA technologies. The perfomance estimations of parallel programs are obtained.

The rest of the paper is organized as follows. The section 1 is dedicated to inverse multilayer gravity problem definition. The section 2 devoted to LM and CLM description. The next section 3 describes a techniques and principles used for program development. The section 4 presents the numerical results using quasi-model gravitational data and the results of parallel implementations. The final section lists the conclusions.

1. Multilayer structural gravity problem statement

The three-dimensional structural inverse gravity problem on finding interfaces between medium layers on the basis of data on the gravitational field measured in a certain area of the earth surface, and the density jumps.

It is assumed that the lower half-space consists of several layers with a constant density Aa i (l = 1 , ..,L ), divided by desired interfaces S i , where L is the number of interfaces (fig. 1). The gravitational effect of such a half-space is equal to the sum of the gravitational effects of all the interfaces.

Fig. 1. Model of multilayer medium

Let the interfaces be described by the equations u i = u i ( x,y ) and the jumps of density are equal to A07. The interfaces have horizontal asymptotic planes u i = H i , i.e.

lim | u i ( x, y ) - H i l =0 . | x | , | y |\rightarrow\infty

Functions u i = u i ( x,y ) describing the desired interfaces satisfy operator equation (2), operator A takes the form

T+

A(u) = E f A"l/ / { i 1

[( x - x ' ) ² + ( y - y ' ) ² + u ² ( x, y )] ¹ / ²

-

[( x - x ' ) ² + (y - y ' ) ² + H l ² ] ^1/2

} = ^A g ⁽ x ,y ' ) ,

where f is the gravitational constant, Act i (1 = 1 , ..,L ) is the density jump, A g ( x ' ,y ' ) = ^ L =1 g i is the sum of an anomalous gravitational fields. Preliminary processing of the gravity data with the aim to select the anomalous field from the measured gravity data is performed using the methodology [8]. The problem is undetermined because of attemption to find several unknown functions u i = u i (x,y) from the given function A g ( x ' ,y ' ). So it’s necessary to use the weight factors which can be found from formula [7].

2. Numerical methods for solving the problem

To solve (6) the regularized Levenberg–Marquardt algorithm with weight factors can be used:

u ^k+1 = u k - ₇ [ A ' ( u ^k ) * A ' (u k ) + „I ] ^{— 1} A[ A ' ( u ^k ) * ( A ( u ^k ) - f ) + a(u - u ⁰ )] , (7) where A is operator with a corresponding diagonal matrix with the weight factors on the main diagonal.

Remark. In nonlinear inverse gravimetry problems in a discrete representation the matrix A ' ( u ^k ) is ill-conditioned which entails significant increasing the condition number of A ' ( u ^k ) * A ' ( u ^k ).

The second method is a Levenberg–Marquardt regularized Levenberg–Marquardt algorithm [2]. Here iterative process approximates each of the solution components u i , l = 1 ,.., L :

-X = u k - 7 -A[ A ' ( u k ) * ( A ( u ^k ) - f ) + „ ( u - u 0 )] ,                 (8)

\varphi l

where

v i = f ^A ^ j ^ K U ^{( x} ' ^,y ' ^,x,y^,u k ^{( x,}y ^{)) dx} ' dy 'j

^x [^{f Aa} / / K U ^{( x,}y^,x ' ^,y ' ^{,u k} ( x^^dxdy],

where K U ( x ' , y ' , x, y, u k ( x,y )) is transposed kernel function of K U (x,y,x,y' ,u k ( x, y )), A ' ( u k ) * is a transposed derivative operator in u _l ^k . The value \varphi l depends on u _l ^k . The process (8) is implemented in discrete form

u k, +¹ = u ki - 7^-W, , L A ' ( u k ) T ( A ( u ^k ) - f ) ) i + „ ( u k, - „ » _ )] ,              (9)

where

v i , i =

NM fActEEKU(xk, y'm, {x, y}i, uiki)Ax'Ay' k=1 m=1

NM x f ActEEKU (xk, ym, {x, y'}i,uk (xk, ym))AxAy , k=1 m=1

Here we don’t need computation of the inverse of matrix A(u^k) T A (u^k ) + al . It makes this method more economical for numerical solution then (7) which computational complexity is O ( n 3 ) because of multiplication A^A k ) T A( u^k ) and matrix A^A k ) T A( u^k ) + al inversion. The computational complexity of (8) is O ( n 2 ) because the most time-consuming operation here is A(u^k) T matrix elements calculation and matrix-vector multiplication.

Discretizing equation (6) on the n = M x N grid with the given right-hand side A g ( x ' , y ' ) and approximating integral operator A ( u ) using the quadrature formula, we obtain the right-hand side F(X, y') of M x N dimension, the solution vector u(x, y) = [ u i ( x, y ) , ..,u l (x, y )] of L x M x N dimension, the derivative matrix of operator A(u ^k ) of (M x N ) x (L x M x N ) dimension, and the system of nonlinear equations

A n [ u ] = F n (10)

The ||A n [ u ^k ] - F n h / h F n | < \varepsilon relative error condition for comparing the exact and numerical solutions with a sufficiently small \varepsilon is taken as the termination criterion.

• 3.    Optimization, parallelization and implementation

  A big size matrices in LM algorithm require large amounts of memory. For example, when L = 3, M = N = 1000 the matrix A(u ^k ) * A ' (u ^k ) type of double allocates « 67 Tb. Also full matrix-matrix multiplication is very computationally expensive problem. So to reduce memory allocation the decision was made to make all matrix-matrix and matrix-vector computations flying: a matrix element is calculated at the time of access to this element. Let it show.

• 4.    Results of numerical experiments

  The structural inverse gravimetry problem of finding model interfaces S 1 , S 2 , S 3 for the four-layer medium with the density jumps was solved using the quasi-model original gravitational data and with uniform noise with an amplitude of 15% noise for the grids 100 x 100 km ² and 1000 x 1000 km ² . The gravitational field (fig. 2) is a real but density jumps are taken from model, the model surfaces are based on the quasi-real surfaces constructed in work [9].

Previously the system of non-linear equations (10) reduces to the SLAE:

B(u ^k )u ^k+1 = [A(u ^k ) T A(u ^k ) + al]u ^k+1 = b, (11)

where b = [ A ' ( u ^k ) ^T A(u ^k ) + al]u ^k — XA(u ^k ) T (A(u ^k ) — f s ). Here we obtain A(u ^k ) T (A(u ^k ) — f s ) and [ A ' ( u ^k ) T A(u ^k )]u ^k on the fly. Within the "associative law" [ A ' ( u k ) T A(u ^k )]u ^k equals to A ' ( u ^k ) ^T [ A ' (u k )u ^k ], so "on the fly"technique makes it possible to avoid matrix to matrix multiplication replacing it matrix-vector twice operation. Further the system (11) can be solved by iterative gradient-type methods, minimal residual method e.g [12, 13]. A method chosen in this work is a minimal residual method.

Parallel algorithms for solving (6) are implemented numerically on the multicore Intel Xeon processor and NVIDIA Tesla M2050 graphics processors unit incorporated in the parallel computing system Uran at the Institute of Mathematics and Mechanics of the Ural Branch of RAS. The parallel algorithms are implemented on the multicore Intel Xeon processor using the OpenMP technology and Intel MKL library and on NVIDIA Tesla GPUs using the CUDA technology and CUBLAS library.

For the multicore Intel Xeon processor, the optimization of the vector-matrix operations using the Intel Xeon compiler options and the loop vectorization using the directive #pragma simd are implemented.

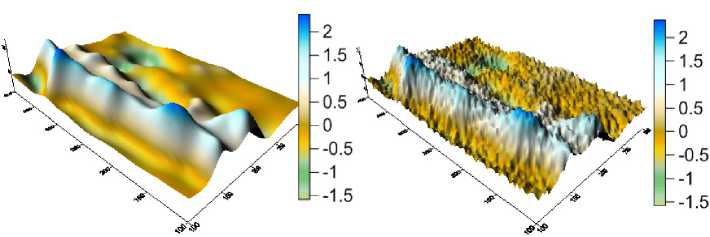
Рис. 2. Total gravitational field (left) and 15% noised total field (right) (mGal)

The distances to the asymptotic planes were taken as H 1 = 8 km, H 2 = 15 km and H 3 = 30 km. The density jumps were \Delta \sigma 1 = 0 , 2 g/cm ³ , \Delta \sigma 2 = 0 , 1 g/cm ³ , \Delta \sigma 3 = 0 , 1 g/cm ³ . The grid steps were equal to \Delta x = 2 km, \Delta y = 3 km.

The part a) of the fig. 3 shows model interfaces S 1 , S 2 , S 3 . The part b) shows reconstructed interfaces by LM and the part c) shows CLM results. The parts d) and c) shows reconstructed interfaces by LM and CLM from noised gravitational field.

The table presents the computation times for solving the gravity problem in the three-layer medium for model interfaces with/without noise by the using LM, CLM methods for the grids of 100 \times 100 and 1000 \times 1000 dimensions. The weight factors were obtained from preliminary selected fields by formula from [7] with parameters \alpha = 1, \beta = 1 , 1. The regularization parameter a = 10 - 3 and the dumping factor 7 = 1 were taken for both methods. The termination criterion \varepsilon was set to 0.25. In the second column of the table number of iterations for gravitational data without noise is written, in the third column number of iterations for gravitational data with 15% noise is shown. The relative errors \delta i = \| u _a - u _e \| / \| u _e \| for comparing the exact u _e and numerical solution u _a for each i layer are shown (for original gravitational data). In the last columns the solution times are shown: T 1 is the solution time on one core of Intel Xeon, T 2 is the solution time on eight cores of Intel Xeon, T 3 is the solution time on NVIDIA Tesla M2050 GPU. Data in the top substrings corresponds to 100 \times 100 grid and data in the bottom substrings corresponds to 1000 \times 1000 grid.

Table

Relative errors and computation times

Method	N 0\%	N 15\%	\delta 1	\delta 2	\delta 3	T 1	T 2	T 3
LM	30	57	0,052	0,026	0.051	4 min. 6 sec.	2 min. 15 sec.	22 sec.
						11 h. 40 min.	1 h. 25 min.	35 min.
CLM	10	19	0,051	0,035	0,060	33 sec.	16 sec.	2 sec.
						1 h. 12 min.	10 min.	3 min.

Conclusion

On a base of Levenberg–Marquardt and componentwise Newton type algorithms a Levenberg–Marquardt method is proposed. This method joins advantages of Levenberg–Marquardt scheme in solving gravity multilayer problem and simlicity in Levenberg–Marquardt apporoach in the Gauss–Newton method. At the same time a regularized Levenberg–Marquardt type method avoids some of the complexities associated with using classic 10 Вестник ЮУрГУ. Серия «Вычислительная математика и информатика»

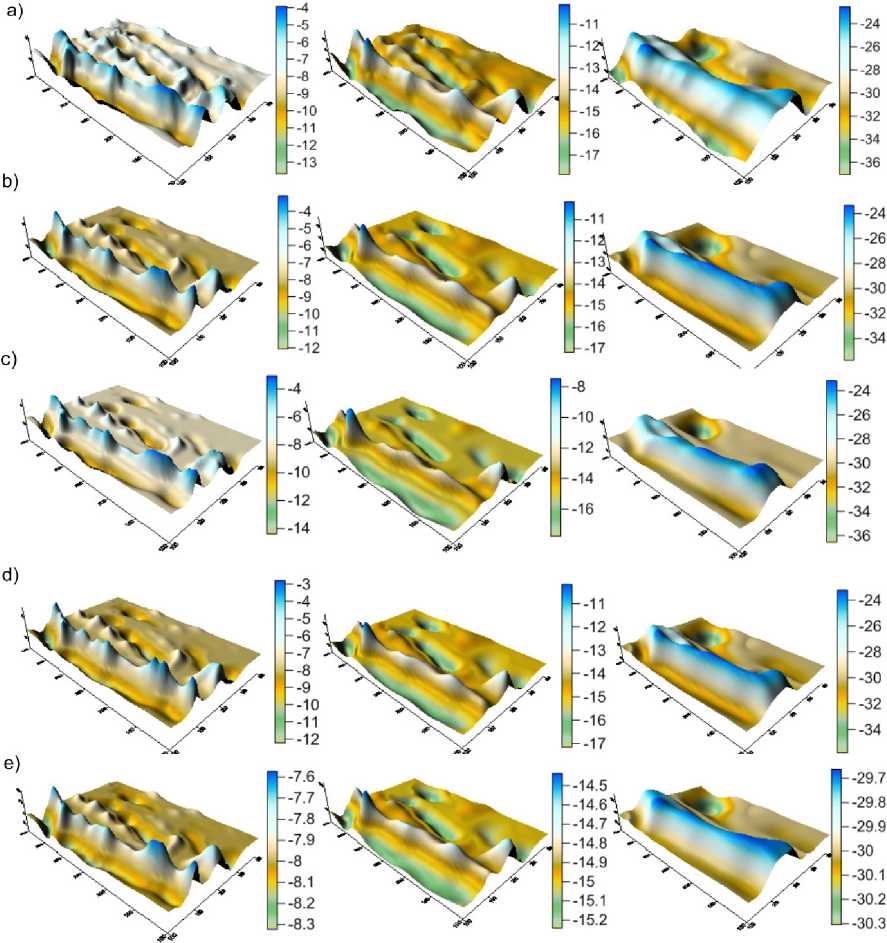
Рис. 3. Comparison of the exact solutions with numerical with parts a) exact solutions, b) numerical LM solutions, c) numerical CLM solutions, d) numerical LM solutions with noised field, e) numerical CLM solutions with noised field

Levenberg–Marquardt method. At first, the inversing an ill-conditioned matrices using internal iterative process. In the second place, matrix-to matrix multiplying entails high computational complexity and big memory consumption. This problem may be solved by "on the fly"technique. The results of numerical experiments show that CLM method has better convergence then classic LM. The both methods are resistant to uniform noise. For large-scale grids, when the data cannot be stored in the memory, "on the fly"technique is the fastest. The computations’ acceleration and efficiency on multi-core and graphic accelerators are sufficient. At small grid sizes, the acceleration S _n < n , where n is the number of processors, but when the grid size increases it is equalized S _n \approx n and an efficiency E _n \approx 1. This means a high resource parallelism of algorithms.

In the future, the question of theoretical interest of the Levenberg–Marquardt method concerns investigating its convergence properties, the conditions on the kernel of the integral operator in equation (1). The obtained conclusions will be useful for another applications.

Acknowledgments.

The author expresses his gratitude to his collegue Vladimir Misilov from the Institute of Mathematics and Mechanics of the UrB of RAS and to the researchers team from Institute of Geophysics of the UrB of RAS for providing gravity data used in section 4. Author expresses his deep appreciation to his scientific adviser Elena Akimova for useful comments.

This work was partly supported by the UrB of the RAS within the framework of the Program of the Presidium RAS (p. 15-7-1-3) and also was partly supported by the RFBR (p. 15-01-00629 А).

This paper is distributed under the terms of the Creative Commons Attribution-Non Commercial 3.0 License which permits non-commercial use, reproduction and distribution of the work without further permission provided the original work is properly cited.