A Review on Gravitational Search Algorithm and its Applications to Data Clustering & Classification
Автор: Yugal kumar, G. Sahoo
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 6 vol.6, 2014 года.
Бесплатный доступ
Natural phenomenon’s and swarms behavior are the warm area of research among the researchers. A large number of algorithms have been developed on the account of natural phenomenon’s and swarms behavior. These algorithms have been implemented on the various computational problems for the sake of solutions and provided significant results than conventional methods but there is no such algorithm which can be applied for all of the computational problems. In 2009, a new algorithm was developed on the behalf of theory of gravity and was named gravitational search algorithm (GSA) for continuous optimization problems. In short span of time, GSA algorithm gain popularity among researchers and has been applied to large number of problems such as clustering, classification, parameter identification etc. This paper presents the compendious survey on the GSA algorithm and its applications as well as enlightens the applicability of GSA in data clustering & classification.
Classification, Clustering, Gravitational Search Algorithm, Optimization, Nature Inspired Algorithm
Короткий адрес: https://sciup.org/15010573
IDR: 15010573
Текст научной статьи A Review on Gravitational Search Algorithm and its Applications to Data Clustering & Classification
Published Online May 2014 in MECS
in 2006 proposed a new algorithm Big Bang Big Crunch (BB-BC) based on the big bang theory (Theory of Evolution of Universe) for optimization problems. BB-BC algorithm is used to solve large numbers of optimization problems such as multi modal optimization problem [35], multi-objective optimization problem [36], clustering [37] etc. A brief description about the nature inspired algorithms has been given above that are used to solve the optimization problems but till date there does not exists any algorithm that can solve the entire optimization problems exactly.
The rest of paper is organized as follows. Section II gives the detail about GSA. Section III describes variants and modifications in GSA. The hybridization of GSA with other techniques is discussed in section IV. Section V and VI focus the application of GSA algorithm in clustering and classification. These sections are followed by conclusion of paper.
-
II. Gravitational Search Algorithm
-
• Identification of search space.
-
• Generate Initial population.
-
• Evaluate fitness function for each particle in population.
-
• Update the gravitational constant value.
G (t) = G (G0, t), Best (t) = min i ∈ {1,…, } Fit i ( t )
Worst (t) = max Fit( t ) i ∈ 1 …․
-
• Calculate the total force in different direction (M) and Acceleration (a) by following equations:
_ mi( t ) Fit; ( t ) -Worst ( t )
M i ( t )= "FT1 ( ) Where m i ( t )= () ( )
∑ () () ( )
Acceleration at ( t )= ^ ( - ) , where Ff ( t )= ( t )
∑ j=i , j^randjFfj ( t )
-
• Update the particle velocity and position. Velocity and position of particle is calculated by following equations:
Velocity ^V ( t +1)= randt × dy ( t )× dta ( t )
Position Xf ( t +1)= Xf ( t )+ VA ( t +1)
-
• Stopping criteria (repeat until stopping criteria met).
18%
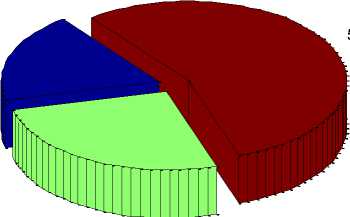
55%
26%
GSA
GSA Variants
Hybrid GSA problems till date as well as to improve the statistics of original GSA.
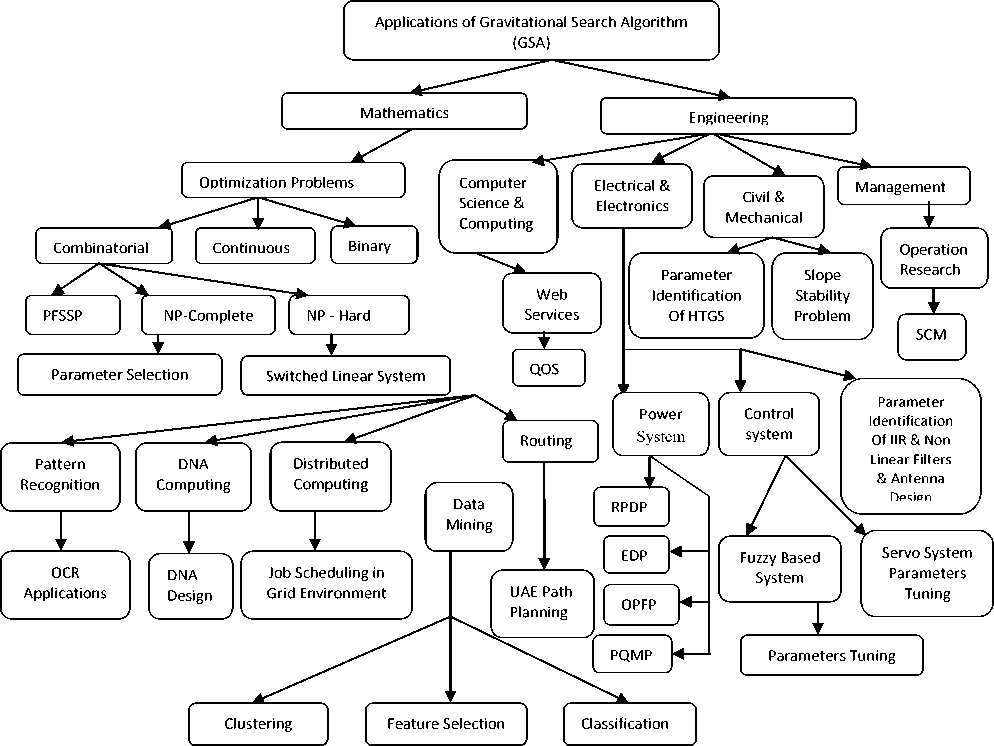
Fig. 1. Applicability of Gravitational Search Algorithm in different domains
Fig. 2. Statistics of Gravitational Search Algorithm
-
III. GSA Variants, Comparisons and
Modifications
-
IV. GSA Hybridization and Applications
Discussion: Lot of algorithms have been developed by the researcher based on the gravitational search algorithm to improve the capabilities of GSA, increases the coverage area of GSA, overcome the limitations of some existed algorithms etc. and compared the performance of GSA to others techniques such as PSO, GA, DE, BBO, ABC etc. in which GSA provided better performance than others. The Table 1 provide the year wise development in the field of gravitational search algorithm as well as the problems addressed by the GSA & GSA based algorithms with performance matrices.
Table1. List of proposed algorithm using GSA and its variants
|
Year |
Author |
Algorithm |
Problem |
Performance Metrics |
|
2009 |
Rashedi et al (2009) |
GSA |
Optimization problems in continuous space |
23 Non linear benchmark functions i.e. unimodal, multi model |
|
2010 |
Rashedi et al (2010) |
BGSA |
Binary optimization Problems |
23 Minimization and 2 maximization benchmark functions |
|
2010 |
Hamid Reza Hassanzadeh et al (2010) |
MOGSA |
Multi Objective optimization problems |
Spacing & gravitational distance criteria |
|
2010 |
Xiangtao Li et al (2010) |
SIGSA |
Permutation flow shop scheduling problem |
29 Problems of two classes of PFSSP such as car1, car2 to car8 etc. |
|
2010 |
A. Chatterjeeet al (2010) |
GSA |
To improve Side lobe in concentric ring arrays(Antenna) |
Fitness Value & Computational Time |
|
2010 |
Seyedali Mirjalili et al (2010) |
PSOGSA |
To avoid slow convergence due to memory less feature of GSA |
23 Non linear benchmark functions i.e. unimodal, multi model |
|
2011 |
Jianhua Xiao and Zhen Cheng (2011) |
GSA |
DNA sequences optimization problem |
Continuity, H- measure and Similarity |
|
2011 |
S. Sarafrazi et al (2011) |
Improved GSA |
To increases the exploration and exploitation ability |
23 Non linear benchmark functions |
|
2011 |
M. Soleimanpour-moghadam et al (2011) |
QGSA |
Position and Velocity of an object in GSA |
Unimodal & multimodal |
|
2011 |
Saeid Saryazdi (2011) |
GSA worked as heuristic search |
Parameter estimation problem of IIR and Nonlinear rational filters |
Unimodal function, multimodal function & complexity of problem |
|
2011 |
Jianhua Xiao et al (2011) |
GCSA |
Partner selection problem with due date constraint |
Cost criteria & convergence rate |
|
2011 |
Radu-Emil Precup et al (2011) |
GSA with modified deprecation equation |
Tuning the fuzzy control systems |
Performance indices |
|
2011 |
Radu-Emil Precup et al (2011) |
GSA with three modifications |
To improve parametric sensitivity |
Performance indices |
|
2011 |
Serhat Duman et al (2011) |
GSA |
Economic Dispatch problem |
Three test system |
|
2011 |
J. P. Papa et al (2011) |
OPF-GSA |
Feature selection Task |
Number of features selected |
|
2011 |
M. Ghalambaz et al (2011) |
HNNGSA |
To solve wessinger’s equation |
……………………………….. |
|
2011 |
Chaoshun Li et al (2011) |
IGSA |
To identify the parameter for hydraulic turbine governing system |
Frequency |
|
2011 |
Abdolreza Hatamlou et al (2011) |
GSA |
Data clustering |
Sum of intra cluster distance and Standard deviation |
|
2011 |
Minghao Yin et al (2011) |
IGSAKHM |
Slow convergence problem of GSA in clustering |
F- measure, run time, mean and standard deviation |
|
2011 |
Abdolreza Hatamlou et al (2011) |
GSA-HS |
Clustering |
Sum of intra cluster distance and center of corresponding cluster |
|
2011 |
Soroor Sarafrazi et al (2011) |
GSA-SVM |
To increases classification accuracy in Binary Problems |
Std. Dev., Mean, Max. & Min. |
|
2012 |
Nihan Kazak et al (2012) |
Modified GSA (MGSA). |
To increases searching and convergence rate |
3 Benchmark functions Such as unimodal, multimodal |
|
2012 |
Mohadeseh Soleimanpour et al (2012) |
Improved QGSA |
Diversity loss problems |
Unimodal & multimodal |
|
2012 |
Lucian-Ovidiu Fedorovici et al (2012) |
GSA with BP |
OCR applications |
Convergence and recognitions rates |
|
2012 |
Nanji H. R et al (2012) |
multi agent based GSA |
Computational cost of original GSA |
Six bench mark functions such as unimodal, multimodal |
|
2012 |
Radu-Emil Precup et al (2012) |
Adaptive GSA |
To minimize the objective function |
Sensitivity |
|
2012 |
S. Duman et al (2012) |
GSA |
Reactive power dispatch problem |
Minimization of system real power, improvement voltage profile & enhancement of voltage |
|
2012 |
Serhat Duman et al (2012) |
GSA |
Optimal Power Flow problem |
IEEE 30 Bus power system including six different cases |
|
2012 |
Chaoshun Li et al ( 2012) |
CGSA |
Parameter identification problem of chaotic system |
|
|
2012 |
Abdolreza Hatamlou et al (2012) |
GSA-KM |
Clustering problem(For improve searching capabilities of GSA) |
Number of steps and cost |
|
2012 |
Chaoshun Li et al (2012) |
GSAHCA |
Identification of T-S fuzzy model |
Model accuracy |
|
2012 |
Hossein Askari et al (2012) |
Intelligent GSA |
Classification of data |
Accuracy, minimum, maximum and average score of recognition |
|
2012 |
Ahmad Asurl Ibrahim et al (2012) |
QBGSA |
Power quality monitor placement (PQMP) problem |
Radial 69 bus distributed system and IEEE 118 bus system with Bolted three phase, Double line to ground and Single phase to ground |
|
2012 |
Hamed Sadeghiet et al (2012) |
GSA with sparse optimization |
Identification of switch linear system and Parameter estimation |
Statistical Robustness under excitation, noise and switching sequence |
|
2012 |
Mohammad Khajehzadeh et al (2012) |
MGSA |
Slope Stability Analysis |
Minimum factor of safety and reliability index |
|
2012 |
Abbas Bahrololoum et al (2012) |
prototype classifier based on GSA |
Data classification |
Average misclassification percentage error |
|
2012 |
Li Pei et al (2012) |
GSA with PSO & DE(IGSA) |
Routing (Path planning for UAE) |
Cost of threats & Evolution Curve |
|
2013 |
Soroor Sarafrazi et al (2013) |
GSA-SVM |
Parameter Setting of SVM & Increased accuracy(Classification) |
Accuracy (Mean & Standard Deviation) |
-
V. GSA in Clustering
Table 2. Comparisons of GSA and its variants to other techniques
|
Method |
Iris |
Wine |
Glass |
CMC |
Cancer |
|||||
|
Avg. |
Std. |
Avg. |
Std. |
Avg. |
Std. |
Avg. |
Std. |
Avg. |
Std. |
|
|
KM |
106.05 |
14.63 |
18061.00 |
793.21 |
235.50 |
12.47 |
5893.60 |
47.16 |
3251.21 |
251.14 |
|
KMH |
113.41 |
0.09 |
18386.00 |
0.00 |
257.18 |
0.00 |
5852.96 |
25.00 |
3234.40 |
0.00 |
|
GA |
125.19 |
14.56 |
16530.53 |
0.00 |
282.32 |
4.14 |
5756.59 |
50.37 |
3249.46 |
229.73 |
|
SA |
99.95 |
2.02 |
17521.09 |
753.08 |
282.19 |
4.24 |
5893.48 |
50.87 |
3239.17 |
230.19 |
|
ACO |
97.17 |
0.37 |
16530.53 |
0.00 |
273.46 |
3.58 |
5819.13 |
45.63 |
3046.06 |
90.50 |
|
HBMO |
96.95 |
0.53 |
16357.28 |
0.00 |
247.71 |
2.44 |
5713.98 |
12.69 |
3112.42 |
103.47 |
|
PSO |
97.23 |
0.35 |
16417.47 |
85.49 |
275.71 |
4.55 |
5820.96 |
46.95 |
3050.04 |
110.80 |
|
GSA |
96.72 |
0.01 |
16376.61 |
31.34 |
225.70 |
3.40 |
5699.84 |
1.72 |
2973.58 |
8.17 |
|
GSA-KM |
96.69 |
0.01 |
16294.31 |
0.04 |
214.22 |
1.14 |
5697.36 |
0.27 |
2965.21 |
0.07 |
|
GSA-KMH |
96.58 |
0.002 |
16234.560 |
0 |
185.710 |
0.035 |
5685.350 |
0.310 |
2954.250 |
0.056 |
|
GSA-HS |
96.65 |
0.0 |
16292 |
0.0 |
---- |
---- |
5693.7 |
0.0 |
2964.4 |
0.0 |
|
PSOGSA |
97.23 |
0.060 |
16331.260 |
0.450 |
205.710 |
2.090 |
5699.100 |
0.540 |
2969.410 |
0.063 |
Discussion : The study of the literature of GSA in clustering, it has been observed that five GSA based algorithms have been proposed to solve the clustering problems. These algorithms are GSA, GSA-KM, GSA-KMH, GSA-HS and PSOGSA. To evaluate the relatively performance of GSA and its variant to others techniques, a table is constructed using common datasets & parameters with help of literature [37,78, 79, 80] and compares the GSA & its variants to other clustering techniques. The table 2 provides the comparisons between the GSA & its variants to other well known techniques that are used to solve the clustering problems. The performance of these techniques evaluate with five different dataset using sum of intra cluster distance & standard deviation parameters. These parameters deduce the efficiency of techniques in data clustering. Minimum value of parameters means better the efficiency of the technique. The GSA provides minimum sum of intra cluster distance with all five datasets as compares to KM, KMH, GA, SA, ACO, HBMO and PSO. To analyze standard deviation parameter, GSA has minimum value for Iris and CMC datasets while second minimum value for all other datasets. So, Table 2 states that GSA provides more accurate and significant result than other techniques except GSA variants. Table 2 also provides the comparisons of different GSA variants i.e. GSA, GSA-KM, GSA-KMH, GSA- HS and PSOGSA. From the table 2, it is conclude that GSA-KMH provides the minimum sum of intra clusters distance and GSA-HS provides almost zero value of standard deviation parameter. The quality of cluster depends on the minimum value of objects from its cluster centroid. So, minimum sum of intra cluster distance mean objects are tightly bound with cluster. From the Table 2, it is observe that GSA-KMH is the best technique among all GSA variants and other nature inspired techniques for clustering problem.
-
VI. GSA in Classification
Discussion: To the depth study of GSA in classification problem, it has been observed that there exist some common data sets on which GSA & its variants compare with other classification methods using some parameters and GSA & its variants provides better performance than others. Such datasets are Iris, wine, glass & cancer and performance of classification methods evaluate with misclassified instance, accuracy, rank parameters etc. Table 3 [66,85, 86, 87] provides the comparisons of GSA & its variants (that are proposed for classification problems) with other techniques using above discussed common datasets with two parameters: accuracy & rank as well as some other methods also include such as ID3, J48, SVM, IBK etc.
ABC (88.92, 5) algorithm get fifth position while multi boost (68.21, 20) provides worst results.
|
Classifiers |
Iris |
Cancer |
Wine |
Glass |
||||
|
Accuracy |
Rank |
Accuracy |
Rank |
Accuracy |
Rank |
Accuracy |
Rank |
|
|
IPS-classifier |
95.3 |
9 |
95.9 |
9 |
94.9 |
6 |
70.1 |
6 |
|
IGA-classifier |
96.7 |
4 |
97 |
6 |
96.4 |
4 |
75.2 |
3 |
|
DE-classifier |
88.7 |
15 |
86.4 |
18 |
86.3 |
7 |
58.4 |
13 |
|
GSA-classifier |
82.6 |
19 |
80.1 |
20 |
61.3 |
17 |
88 |
1 |
|
IGSA-classifier |
98.1 |
2 |
96.1 |
8 |
97.6 |
2 |
79.5 |
2 |
|
PSO |
96.14 |
6 |
95.74 |
10 |
96.22 |
5 |
60.33 |
9 |
|
ABC |
100 |
1 |
100 |
1 |
97.19 |
3 |
58.5 |
12 |
|
GSA Prototype |
97.54 |
3 |
99.37 |
3 |
97.64 |
1 |
67.67 |
7 |
|
GSA-SVM (GSA+BGSA) |
- |
- |
99.54 |
2 |
- |
- |
- |
- |
|
GSA-SVM |
- |
- |
99.37 |
3 |
- |
- |
- |
- |
|
Bayes Net |
95.77 |
7 |
80.26 |
19 |
70.2 |
9 |
75.02 |
4 |
|
MLP ANN |
93.96 |
11 |
97.07 |
5 |
66.12 |
12 |
64.61 |
8 |
|
RBF |
91.66 |
14 |
79.33 |
21 |
60.55 |
18 |
55.56 |
14 |
|
K-Star |
93.26 |
13 |
97.56 |
4 |
64.22 |
14 |
60.28 |
10 |
|
Bagging |
96.58 |
5 |
95.53 |
13 |
63.76 |
16 |
50 |
16 |
|
Multi Boost |
68.4 |
20 |
93.91 |
15 |
64.22 |
14 |
46.3 |
18 |
|
NB Tree |
94.73 |
10 |
92.31 |
16 |
68.12 |
10 |
71.12 |
5 |
|
SMO (SVM) |
88.66 |
16 |
95.7 |
11 |
66.51 |
11 |
51.4 |
15 |
|
IBK |
85.33 |
18 |
95.56 |
12 |
65.1 |
13 |
58.87 |
11 |
|
Dagging |
86 |
17 |
96.7 |
7 |
64.2 |
15 |
46.72 |
17 |
|
J48 |
95.33 |
8 |
94.42 |
14 |
64.2 |
15 |
37.38 |
19 |
|
ID3 |
93.55 |
12 |
92.24 |
17 |
72.34 |
8 |
36.56 |
20 |
Table 4. Average accuracy result with relative ranking of datasets
|
Parameter |
Classifiers |
|||||||
|
IPS |
IGA |
DE |
GSA |
IGSA |
PSO |
ABC |
GSA Prototype |
|
|
Average Accuracy |
89.05 |
91.33 |
79.95 |
78 |
92.83 |
87.11 |
88.92 |
90.56 |
|
Rank |
4 |
2 |
10 |
12 |
1 |
6 |
5 |
3 |
Table 5. Average accuracy result with relative ranking of datasets
|
Parameter |
Classifiers |
|||||
|
Bayes Net |
MLP ANN |
RBF |
K-Star |
Bagging |
Multi Boost |
|
|
Average Accuracy |
80.31 |
80.44 |
71.78 |
78.83 |
76.47 |
68.21 |
|
Rank |
9 |
8 |
19 |
11 |
13 |
20 |
Table 6: Average accuracy result with relative ranking of datasets
|
Parameter |
Classifiers |
|||||
|
NB Tree |
SMO |
IBK |
Dagging |
J48 |
ID3 |
|
|
Average Accuracy |
81.57 |
75.57 |
76.22 |
73.41 |
72.83 |
73.67 |
|
Rank |
7 |
15 |
14 |
17 |
18 |
16 |
|
Sum of Ranks |
Classifiers |
|||||||
|
IPS |
IGA |
DE |
GSA |
IGSA |
PSO |
ABC |
GSA Prototype |
|
|
Sum of Ranks |
29 (6) |
16 (3) |
52 (11) |
56 (14) |
12 (1) |
19 (5) |
17 (4) |
13 (2) |
|
Sum of Ranks |
Classifiers |
|||||
|
Bayes Net |
MLP ANN |
RBF |
K-Star |
Bagging |
Multi Boost |
|
|
Sum of Ranks |
38(8) |
35 (7) |
66 (15) |
40 (9) |
49 (10) |
66 (15) |
|
Sum of Ranks |
Classifiers |
|||||
|
NB Tree |
SMO |
IBK |
Dagging |
J48 |
ID3 |
|
|
Sum of Ranks |
40 (9) |
52 (11) |
53 (12) |
55 (13) |
55 (13) |
56 (14) |
-
VII. Conclusion
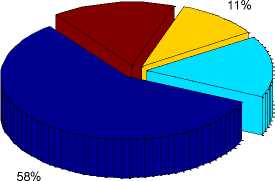
This paper presents the review of pervious research in the field of gravitational search algorithm, its variants; hybridize GSA and its applications. Table 1 provides the complete summary of GSA literature, modification in GSA and applications of GSA. From the table 1, it conclude that GSA is four years old but this field shows tremendous growth & quite popular between researchers and large number of problems solved by GSA such as RPDP, ED, OPF and many more mentioned in table 1. The figure 1 shows the percentage of hybrid algorithms and modification in GSA has been proposed by various authors in GSA literature. The modification and hybridization of GSA with other techniques provided better results in terms of computational time, convergence etc. The figure 3 provides the year wise development in the field of gravitational algorithms and number of publications in each year published with the help of GSA. From the figure 3, it’s conclude that there is only one publication on GSA in year 2009 but in last two years large number of papers published using GSA that shows the wide popularity of GSA among researchers. The figure 4 categorizes the publications based on GSA in different domains. The figure 4 states that half of GSA publications related to computer science and computing filed that shows the GSA applicability and significance in computer science & computing field. The twenty four percent of GSA publications come from optimization & others field and very less publication from civil & mechanical field. From the figure 4, it is
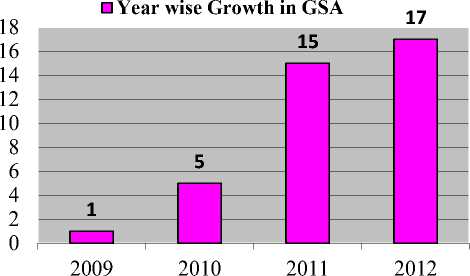
Fig. 3. Year wise growth in GSA
24%
50%
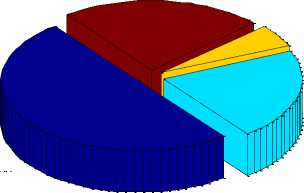
5%
21%
। । Optimization & Others
Fig. 4. Categorization of GSA publications
^e Data mining ANN i i Computing
^e Others
Список литературы A Review on Gravitational Search Algorithm and its Applications to Data Clustering & Classification
- W. Du, B. Li,”Multi-strategy ensemble particle swarm optimization for dynamic optimization”, Information Sciences, 2008, 178, pp 3096–3109.
- X. Yao, Y. Liu, G. Lin,”Evolutionary programming made faster”, IEEE Transactions on Evolutionary Computation, 1999, 3 pp 82–102.
- Y. Liu, Z. Yi, H. Wu, M. Ye, K. Chen, “A tabu search approach for the minimum sum-of-squares clustering problem”, Information Sciences, 2008, 178, 2680–2704.
- X. Tan, B. Bhanu, “Fingerprint matching by genetic algorithms”, Pattern Recognition, 2006, 39, 465–477.
- T.H. Kim, I. Maruta, T. Sugie,”Robust PID controller tuning based on the constrained particle swarm optimization”, Automatica, 2008, 44, 1104–1110.
- Z. Baojiang, L. Shiyong,”Ant colony optimization algorithm and its application to neuro-fuzzy controller design”, Journal of Systems Engineering and Electronics 18, 603–610.
- O. Cordon, S. Damas, J. Santamarı,”A fast and accurate approach for 3D image registration using the scatter search evolutionary algorithm, Pattern Recognition Letters, 2006, 27 ,pp 1191–1200.
- H. Nezamabadi-pour, S. Saryazdi, E. Rashedi,” Edge detection using ant algorithms”, Soft Computing, 2006, 10, pp 623- 628.
- JY Wu,”MIMO CMAC neural network classifier for solving classification problems”, Applied Soft Computing, 2011, 11 (2), pp 2326–2333
- Kalinlia A, Karabogab N, “Artificial immune algorithm for IIR filter design”, Engineering Applications of Artificial Intelligence, 2005, 18, 919–929.
- D. Karaboga, C. Ozturk (2011) A novel clustering approach: artificial bee colony (ABC) algorithm. Applied Soft Computing 11 (1), pp 652–657.
- Kirkpatrick S, Gelatt CD and Vecchi P,”Optimization by simulated annealing”, Science, 1983, 220, 671-680.
- Mitra D, Romeo F and Vincentelli, A.S., “Convergence and Finite-Time Behavior of Simulated Annealing Advances in Applied Probability”, 1986.
- Janson S & Middendorf M, “A hierarchical particle swarm optimizer for dynamic optimization problems”, In: Proceedings of the application of evolutionary computing, 2004, volume 3005. pp 513–524.
- Kennedy J & Eberhart R, “Particle swarm optimization”, In: Proceeding of IEEE int’l. Conf. on neural networks, 1995, Vol. IV, pp. 1942–1948.
- Silva A, Neves A, Costa E,”Chasing the swarm: a predator pray approach to function optimization”, In: Proceeding of the international conference on soft computing MENDEL, 2002.
- Y.L. Lin, W.D. Chang, J.G. Hsieh,”A particle swarm optimization approach to nonlinear rational filter modeling, Expert Systems with Applications, 2008, 34, pp 1194–1199.
- Holland JH, “Adaptation in natural and artificial systems”, University of Michigan Press, 1975.
- Boeringer D-W, Werner DH, “Particle swarm optimization versus genetic algorithm for phased array synthesis”, IEEE Trans Antennas Propag., 2004, 52(3):771–779.
- Dorigo M,“Optimization, learning and natural algorithms”, PhD thesis, Dipartimento di Elettronica, Politecnico di Milano, Italy, 1992.
- Dorigo M and Gambardella LM, “Ant colony for the traveling salesman problem”, Bio systems, 1997, 43, pp. 73-81.
- Costa, D. and Hertz, A. (1997) Ants can color graphs. J. Operate Res. Soc., 48, pp. 295-305.
- Di Caro G. and Dorigo M. (1998) Two ant colony algorithms for best-effort quality of service routing. In: Unpublished at ANTS'98-From Ant Colonies to Artificial Ants: First International Workshop on Ant Colony Optimization.
- Merkle D & Middendorf M.Modelling,” ACO: Composed permutation problems”, In: Ant algorithms Proceedings of ANTS 2002—Third international workshop. Lecture Notes in Comput Sci, 2002, vol, 2463., pp. 149–62.
- Gutjahr WJ, “A graph-based ant system and its convergence Future Generat. Comput. Syst., 2000, 16(9):873–88.
- Gutjahr WJ, “ACO algorithms with guaranteed convergence to the optimal solution”, Information Process Letters, 2002, 82(3), 145–53.
- Karaboga D, Basturk B,”A powerful and efficient algorithm for numerical function optimization:artificial bee colony (abc) algorithm”, J Glob Optim. 2007b, 39:459–471.
- Karaboga D & Basturk B,”A comparative study of artificial bee colony algorithm”, Applied Mathematics and Computation, 2009, 214:108–32.
- Akay B, Karaboga D , “A modified artificial bee colony algorithm for real-parameter optimization” Inf Sci., 2010 doi:10 .1016/j.ins.2010.07.015.
- Basturk B, Karaboga D, “An artificial bee colony (abc) algorithm for numeric function optimization’, In: IEEE swarm intelligence symposium 2006, Indianapolis, IN, USA.
- Mezura-Montes E, Damian-Araoz M, Cetina-Domingez O ,” Smart flight and dynamic tolerances in the artificial bee colony for constrained optimization”, In: 2010 IEEE congress on evolutionary computation (CEC), 2010, pp 1–8.
- Eduardo Gerhardt and Herbert Martins Gomes, “Artificial Bee Colony (ABC) Algorithm for Engineering Optimization”, Problems In: Proceeding of 3rd International Conference on Engineering Optimization Rio de Janeiro, Brazil, 2012.
- Zhu GP & Kwong S,”Gbest-guided artificial bee colony algorithm for numerical function optimization”, Applied Mathematics and Computation 2010, doi: 10.1016/j.amc.2010 .08.049.
- Osman K. Erol and Ibrahim Eksin,”A new optimization method: Big Bang–Big Crunch”, Advances in Engineering Software, 2006, 37, pp. 106–111.
- Hesheng Tang, Jin Zhou, Songtao Xue and Liyu Xie, ”Big Bang-Big Crunch optimization for parameter estimation in structural systems”, Mechanical Systems and Signal Processing, 2010, 24, pp 2888–2897.
- M.H. Afshar and I. Motaei,”CONSTRAINED BIG BANG-BIG CRUNCH ALGORITHM FOR OPTIMAL SOLUTION OF LARGE SCALE RESERVOIR OPERATION PROBLEM”, Int. J. Optim. Civil Eng., 2011, 2, pp 357-375.
- Hatamlou A, Abdullah S and Othman Z , “Gravitational Search Algorithm with Heuristic Search for Clustering Problems”, In proceeding of 3rd IEEE on Data Mining and Optimization (DMO), 2011, pp. no. 190 – 193, 28-29 June 2011, Selangor, Malaysia.
- Rashedi E, Nezamabadi-pour H, Saryazdi S,” GSA: a gravitational search algorithm”, Information Science, 2009, 179, 2232–2248.
- Holliday D, Resnick R and Walker J, “Fundamentals of physics”, John Wiley and Sons, 1993.
- Schutz B.,” Gravity from the Ground Up”, Cambridge University Press, 2000.
- Rashedi E, Nezamabadi-pour H, Saryazdi S ,”BGSA: binary gravitational search algorithm”, Nat Comput, 2010, 9, pp 727–745.
- Hamid Reza Hassanzadeh and Modjtaba Rouhani, “A MULTI OBJECTIVE GRAVITATIONAL SEARCH ALGORITHM”, In: Proceeding of Second International Conference on Computational Intelligence, Communication Systems and Networks, 2010, pp. 7 – 12.
- S. Sarafrazi, H. Nezamabadi-pour and S. Saryazdi, ”Disruption: A new operator in gravitational search algorithm. Scientia Iranica D, 2011, 18 (3), pp. 539–548.
- M. Soleimanpour-moghadam, H. Nezamabadi-pour, M. M. Farsangi ,”A quantum behaved gravitational search algorithm”, In: proceeding of Int. Conf. Computational Intelligence and Software Engineering, Wuhan, China, 2011.
- Radu-Emil Precup, Radu-Codruţ David, Emil M. Petriu , Stefan Preitl and Mircea-Bogdan Rădac,”Gravitational Search Algorithm in Fuzzy Control Systems Tuning”, In: Proceeding of 18th IFAC World Congress, 2011, pp. no. 13624-13629, Milano (Italy).
- Nihan Kazak and Alpaslan Duysak,”Modified Gravitational Search Algorithm”, In: Proceeding of IEEE International Symposium on Innovations in Intelligent Systems and Applications (INISTA), 2012, pp. 1- 4, Turkey.
- Mohadeseh Soleimanpour moghadam & Hossein Nezamabadi pour, “An improved quantum behaved gravitational search algorithm”, In: proceeding of 20th Iranian Conference on Electrical Engineering, (ICEE2012), 2012, pp. no. 711 – 715.
- Nanji H. R., Mina Sohrabi and Esmat Rashedi,”A High-Speed, Performance-Optimization Algorithm Based on a Gravitational Approach”, Journal of Computing in Science & Engineering, 2012, volume 14, Issue: 5 pp. 56 – 62.
- Xiangtao Li, Jianan Wang, Junping Zhou and Minghao Yin,”An Effective GSA Based Memetic Algorithm for Permutation Flow Shop Scheduling. In: proceeding of IEEE congress on Evolutionary Computation, 2010, pp. no. 1-6.
- Seyedali Mirjalili and Siti Zaiton Mohd Hashim,” A new hybrid PSOGSA algorithm for function optimization”, In: Proceeding of International conference on computer and information application (ICCIA), 2010, pp. no. 374- 377.
- Chatterjee A, Mahanti G. K. and Pathak N, (2010),” COMPARATIVE PERFORMANCE OF GRAVITATIONAL SEARCH ALGORITHM AND MODIFIED PARTICLE SWARM OPTIMIZATION ALGORITHM FOR SYNTHESIS OF THINNED SCANNED CONCENTRIC RING ARRAY ANTENNA”, Progress In Electromagnetic Research B, Vol. 25, 331-348.
- Radu-Emil Precup, Radu-Codruţ David, Emil M. Petriu , Stefan Preitl and Adrian Sebastian Paul,”Gravitational Search Algorithm-Based Tuning of Fuzzy Control Systems with a Reduced Parametric Sensitivity”, Advances in Intelligent and Soft Computing, 2011, Volume 96, pp. 141-150.
- Jianhua Xiao, Fan Qi, and Yongkai Li, “Gravitational Chaotic Search Algorithm for Partners Selection with Due Date Constraint in Virtual Enterprise”, In: Proceeding of Fourth International Workshop on Advanced Computational Intelligence, 2011, pp. 138 – 142.
- J. P. Papa, A. Pagnin, S. A. Schellini, A. Spadotto, R. C. Guido, M. Pont, G. Chiachia and A. X. Falcaoi,”FEATURE SELECTION THROUGH GRAVITATIONAL SEARCH ALGORITHM”, In: Proceeding of IEEE international conference Acoustics, Speech and Signal Processing (ICASSP), 2011, pp. 2052 – 2055.
- M. Ghalambaz, A.R. Noghrehabadi, M.A. Behrang, E. Assareh, A. Ghanbarzadeh, N.Hedayat,”A Hybrid Neural Network and Gravitational Search Algorithm (HNNGSA) Method to Solve well known Wessinger's Equation”, World Academy of Science, Engineering and Technology, 2011, issue 49, pp. no. 803 – 807.
- Chaoshun Li and Jianzhong Zhou , “Parameters identification of hydraulic turbine governing system using improved gravitational search algorithm”, Energy Conversion and Management, 2011, Volume 52, Issue 1, pp. 374–381.
- Jianhua Xiao and Zhen Cheng,”DNA Sequences Optimization Based on Gravitational Search Algorithm for Reliable DNA computing In: proceeding of IEEE Sixth International Conference on Bio-Inspired Computing: Theories and Applications, 2011, pp. 103 – 107.
- Esmat Rashedi, Hossien Nezamabadi-pour and Saeid Saryazdi,”Filter modeling using gravitational search algorithm Engineering applications of Artificial Intelligence, 2011, volume 24(1), pp 117-122.
- Serhat DUMAN, Aysen Basa ARSOY and Nuran YÖRÜKEREN ,”Solution of Economic Dispatch Problem using Gravitational Search Algorithm”, In: Proceeding of 7th international conference of electrical and electronics engineering, 2011, pp. 54 – 59, Turckey.
- Chaoshun Li, Jianzhong Zhou, Jian Xiao and Han Xiao (2012)Parameters identification of chaotic system by chaotic gravitational search algorithm. Chaos, Solitons & Fractals, Volume 45, Issue 4, Pages 539–547, 2012.
- Radu-Emil Precup, Radu-Codruţ David, Emil M. Petriu , Stefan Preitl and Mircea-Bogdan Radac,”Novel Adaptive Gravitational Search Algorithm for Fuzzy Controlled Servo Systems”, IEEE Transcation on Industrial Informatics, 2012, volume 8, no. 4, pp 791 -800.
- Lucian Ovidiu Fedorovici, Radu-Emil Precup, Florin Dragan, Radu-Codrut David and Constantin Purcaru ,”Embedding Gravitational Search Algorithms in Convolutional Neural Networks for OCR Applications In: Proceeding of 7th IEEE International Symposium on Applied Computational intelligence and Informatics, 2012, pp. 125 – 130.
- S. Duman, Y. So nmez, U. Gu venc and N. Yo ru keren, “Optimal reactive power dispatch using a gravitational search algorithm”, IET Gener. Transm. Distrib., 2012, Vol. 6 (6), pp. 563–576.
- Serhat Duman, Ugur Guvenc, Yusuf Sonmez and Nuran Yorukeren,”Optimal power flow using gravitational search algorithm”, Energy Conversion and Management, 2012, volume 59, pp 86–95.
- Asrulibrahim A, Mohamed and Shareef H, ”Application of quantum-inspired binary gravitational search algorithm for optimal power quality monitor placement. In: proceedings of the 11th WSEAS international conference on Artificial Intelligence, Knowledge Engineering and Database,”, 2012, pp. no. 27- 32.
- Hossein Askari and Seyed-Hamid Zahiri, “Decision function estimation using intelligent gravitational search algorithm”, Int. J. Mach. Learn. & Cyber, 2012, 3, pp. 163–172.
- Mohammad Khajehzadeh, Mohd RaihanTaha, Ahmed El-Shafie and MahdiyehEslami, “A modified gravitational search algorithm for slope stability analysis”, Engineering Applications of Artificial Intelligence (article in press)
- Hamed Sadeghi, Najmeh Eghbal and Reyhaneh Kardehi Moghaddam, “Application Gravitational Search Algorithm in Identification of Switched Linear Systems”, In: Proceeding of IEEE Third International Conference on Intelligent Systems Modeling and Simulation, 2012, pp. 89 – 95.
- LI Pei & Duan HaiBin,”Path planning of unmanned aerial vehicle based on improved gravitational search algorithm”, Science China published by Springer, 2012, Vol.55 No.10: 2712–2719.
- M. Mahdavi (2008) Novel meta-heuristic algorithms for clustering web documents. Applied Mathematics and Computation, 208, 201 (1–2), pp 441–451.
- R. Gil-Garcia, A. Pons-Porrata,”Dynamic hierarchical algorithms for document clustering, Pattern Recognition Letters, 2010, 31 (6), pp 469–477.
- Tan P N, Steinbach M & Kumar, “Introduction to data mining, Boston: Addison Wesley, 2005, pp. 487–559.
- Tjhi W C & Chen L H,”A heuristic-based fuzzy co-clustering algorithm for categorization of high-dimensional data”, Fuzzy Sets and Systems, 2008, 159(4), pp 371–389.
- P. Jin, Y.L. Zhu, K.Y. Hu,”A clustering algorithm for data mining based on swarm intelligence”, in: Proceedings of the Sixth International Conference on Machine Learning and Cybernetics, ICMLC, 2007.
- Zhang B, Hsu M & Dayal U,”K-harmonic means – a data clustering algorithm”, Technical Report HPL-1999-124, Hewlett-Packard Laboratories.
- P.S. Shelokar, V.K. Jayaraman, B.D. Kulkarni, “An ant colony approach for clustering”, Analytica Chimica Acta, 2004, 509 (2),pp 187–195.
- Zhou H & Liu YH,”Accurate integration of multi-view range images using k-means clustering. Pattern Recognition, 2008, 41(1), pp 152–175.
- Hatamlou A, Pour HN and Abdullah S, ” Application of gravitational search algorithm on data clustering In: published in proceeding of 6th international workshop on Rough Set and Knowledge technology (RSKT-11), 2011, pp. no. 337-346.
- Hatamlou A, Abdullah S and Pour HN, “ A combined approach for clustering based on K-means and gravitational search algorithms”, Swarm and Evolutionary Computation, 2012, 6, pp 47–52.
- Minghao Yin, Yanmei Hu, Fengqin Yang, Xiangtao Li and Wenxiang Gu,”A novel hybrid K-harmonic means and gravitational search algorithm approach for clustering”, Expert Systems with Applications, 2011, 38, 9319–9324.
- M.W. Kurzynski, “The optimal strategy of a tree classifier”, Pattern Recognition, 1983, 16, pp 81–87.
- F. Seifi, M.R. Kangavari, H. Ahmadi, E. Lotfi, S. Imaniyan, S. Lagzian, “Optimizing twins decision tree classification using genetic algorithms”, In: 7th IEEE International Conference on Cybernetic Intelligent Systems, 2008, pp. 1–6.
- P. Knagenhjelm, P. Brauer,”Classification of vowels in continuous speech using MLP and a hybrid network”, Speech Communication,1990, 9 (1) pp 31–34.
- Rana S, Jasola S and Kumar R A review on particle swarm optimization algorithms and their applications to data clustering Artif Intell Rev, 201,1 35, 211–222.
- Soroor Sarafrazi and Hossein Nezamabadi-pour, “Facing the classification of binary problems with a GSA-SVM hybrid system”, Mathematical and Computer Modeling, 2013, vol. 57, issue 1, pp. 270–278.
- Bahrololoum A, Pour HN, Bahrololoum H and Saeed M, “A prototype classifier based on gravitational search algorithm”, Applied Soft Computing , 2012, 12, 819–825.
- Soroor Sarafrazi, Hossein Nezamabadi-pour and Mojgan Barahman,”A GSA-SVM HYBRID SYSTEM FOR CLASSIFICATION OF BINARY PROBLEMS”, In: Proceedings of the Fourth Global Conference on Power Control and Optimization, 2011, pp. 198-203.


