A Review on Large Scale Graph Processing Using Big Data Based Parallel Programming Models

Published Online February 2017 in MECS

Graphs are of great interest in modeling of complicated structures, such as circuits, protein structures, biological networks, social networks, chemical compounds, the Web, workflows, and XML documents. Graph mining has become an active and important subarea in data mining with the increasing demand on the analysis of large amounts of graph formatted structured data. For further developments in this area, users have to adopt an efficient platform to do their analytic jobs, and developers and system designers have to find a way to measure the performance and other non-functional aspects of interest. Many real world graphs like social networks and communication networks are so big that they require specialized methods for processing and analytics. For example Facebook and Google generate large graphs with which analytics may involve lot of both data and computation intensive tasks. Many of the graph structures involve multiple relationships between vertices which increases the complexity of system. The scalability of the algorithm with respect to graph size is another challenge to be considered. Big graphs challenge our conventional way of thinking on both computer architecture and algorithms as they are difficult to parallelize, dynamic in nature and most of the graph algorithms require very little computation per vertex.

MapReduce[11]model developed at Google gained great attention from various business and scientific domains and has been established as a standard for the processing of large volumes of data which is now called as ‘Big Data’. The MapReduce model has been reimplemented by Apache as an open source framework named Hadoop. Currently Hadoop can be used to perform analytic on petabytes of data using commodity hardware. However existing practices of MapReduce have significant drawbacks which will be described in detail in later part of this paper. Google developed a new programming model named Pregel which implements the Bulk Synchronous Model for parallel computing. Pregel [4] used message passing interface as communication primitive and distributed memory of the nodes in the cluster for graph storage. Apache Giraph, Hama ,GraphLab and Graphx are some open source implementations which support BSP model in which Hama is a pure BSP engine and Giraph , Graphlab and Graphx are specialized graph analytic engines. As many of the scientific and business domains demands analysis of big graphs, the choice of right platform for analyzing such graphs is important. Moreover as the graph structured data holds complex properties like power law distributions, the frameworks for analyzing large graphs are still evolving.

The content of our work can be summarized as follows. The work is to compare how well the Big Data based parallel programming models are suited for analyzing large graphs. Both Big Data based parallel programming models, MapReduce and BSP have been implemented in Hadoop/Giraph environment and the result and feature comparisons are presented in this paper. The graph triangle counting problem, which is widely used in social network analysis is considered as the benchmark problem for experiments. Both the approaches are tested with datasets of various domains.

• II.    Related Work

Three design patterns (In-Mapper Combining, Shimmy and Range Partitioning) that are broadly applicable to MapReduce graph algorithms[1] were developed to improve the efficiency of MapReduce based graph algorithms. A MapReduce algorithm for counting triangles[2] which is used to compute the clustering coefficients in a graph has been proposed. The work mainly discusses two methods, in which the first method MR-NodeIterator is a specialized algorithm designed explicitly for computing the triangles incident on every vertex. The second approach, MR-GraphPartition provides a MapReduce version of a general triangle counting algorithm. [3] has provided a formal definition of Bulk Synchronous Model of parallel computation. The Bulk Synchronous Parallel (BSP) was introduced as a bridging model for designing parallel algorithms. Researchers at Google[4] provided a description about the graph analytic engine called Pregel developed at Google. Pregel provides a fault-tolerant framework for the execution of graph algorithms in parallel over many machines. Algorithms discussed in this work are PageRank, Semi Clustering and Bipartite Matching. David and David [5] investigated the algorithmic effects of the BSP model for graph algorithms and compared the performance with open source software using GraphCT. The work provides a description about the differences in scalability between BSP and shared memory algorithms and also finds that scalable performance can be obtained with graph algorithms in BSP model on Cray XMT. Giving importance to Apache Giraph and GraphLab, Sherif[6] compared open source solutions for processing large amounts of graph structured data. In this work the author has pointed out the drawbacks of MapReduce in graph processing and then explored platforms under development to tackle the graph analytic challenge. The work has also provided PageRank and Shortest Path algorithm in both Giraph and GraphLab. Giraph[7] is a distributed and scalable BSP cluster implementation, which uses commodity hardware with abstraction on load distribution and can support parallelism in a fault tolerant way. Three parallel computing techniques, MapReduce, map-side join and Bulk Synchronous Parallel models were compared and tested[8] for two distinct graph problems (single source shortest path and Collective classification) and found that iterative graph processing with the BSP implementation significantly outperforms MapReduce.

• III.    Parallel Programming Models

Parallel processing can be defined as the processing of program instructions and data by dividing them across various processors and storage systems respectively. Different types of parallel processing systems involve using bit level, instruction level, data level and task level parallelism. A programming model which supports writing programs whose instructions and data which can be processed in parallel at different processors is called a parallel programming model. The choice of a parallel programming model depends upon whether the problem we are dealing with is a computation intensive or data intensive problem. As we have entered the era of Big Data the need for using parallel processing systems for analyzing and mining large volume of diverse and complex data gained importance .As a result most of the data scientists are interested in writing programs and developing frameworks that can exploit data parallel systems. Here our main focus is about programming on data parallel systems which performs parallel processing over data which are distributed across various computing nodes. A comprehensive technical discussion of Big Data based parallel processing platforms which can be used for large graph processing is given in table1.This section describes the general features and dissimilarities between the two Big Data based programming models, MapReduce and BSP with respect to graph processing. An extended version of MapReduce called iterative MapReduce[9] is not discussed in this section as it can make only slight improvement while performing graph processing.

• A.    MapReduce

MapReduce has its roots from functional programming paradigm which is especially designed for distributed computation over massively large datasets which involves a lot of data intensive tasks. The main functions of MapReduce is to queue up, split and parallelize a computation over a cluster of machines in a fault tolerant way. The platforms supports user defined implementations of map and reduce functions. These functions can be provided with partitions of data as input. It also support a system defined shuffle and sort phase and a combiner module for combining intermediate results from mappers. The map phase process the data on nodes in parallel and the reducer aggregates the results. MapReduce is well suited for problems with large number of independent computations which can run in parallel and by design it is tuned for reliability and not for efficiency. MapReduce is a well developed and tested concept and even if it is not originally developed to process graphs, we can adopt several design patterns like schimmy and range partitioning which can improve the efficiency of MapReduce based graph algorithms. Iterative graph algorithms can be implemented as a chain of MapReduce jobs where each job produces an intermediate solution. The general setting of MapReduce model for graph processing is represented in Fig. 1. The entire structure of the graph and other data should be transferred over the network of computing nodes from mapper to reducer during each iteration and should be reassigned at every job in the MapReduce chain. The intermediate result from each job makes the system disk expensive but it can be overcome by using an iterative MapReduce extension. We can store a portion of the graph structure information in every machine and can access reduce function with remote reads by using schimmy pattern but may affect the fault tolerance.

Table 1. Summary of Big Data Processing Platforms

Platform	Features
Hadoop	Open source, De-facto for batch processing, Based on MapReduce programming, Not well suited for computation intensive jobs due to I/O overhead.
Yarn	Next generation hadoop, Resource and job manager for hadoop. Uses the mapreduce execution engine and can support other execution engines also.
Giraph	Open source, In-memory system for synchronous graph specific computations, Based on BSP programming model, Uses the Pregel vertex centric architecture
Twister	Open source, In-memory system which implements the iterative mapreduce concept.
GraphLab	Open source, Supports asynchronous graph specific computations, Based on BSP programming model
Azure	Microsoft’s Cloud computing platform , Can support both data intensive and computation intensive tasks
Spark	Open Source, Multi-stage in memory system, Based on resilient distributed datasets, Good performance over iterative and machine learning algorithms.
Graphx	Distributed graph processing framework on the top of spark. Support data parallel and graph parallel computations, Implements the Pregel BSP API.
Neo4j	Database for graph storage and analytics.

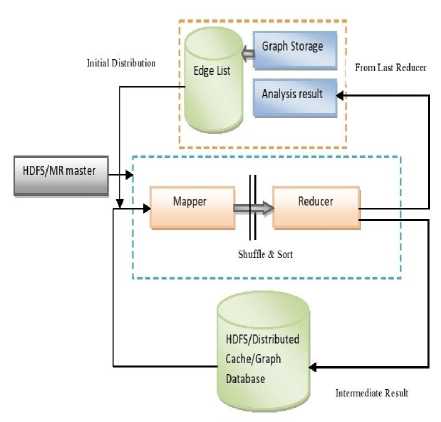
Fig.1. MapReduce Model in Graph Processing

• B.    Bulk Synchronous Parallel (BSP)

BSP is a parallel computing model proposed by Valiant in which a parallel computation process is defined as series of global supersteps. Each superstep involves a concurrent computation phase which is done in parallel by all processors, a global communication phase in which processors exchange data and a synchronization phase at the end of every superstep. Google developed a fault tolerant and distributed computing framework for parallel graph processing called Pregel by gaining inspirations from the BSP model. Later many open source tools were developed by following Pregel framework. The BSP model for parallel processing is showed in Fig. 2.

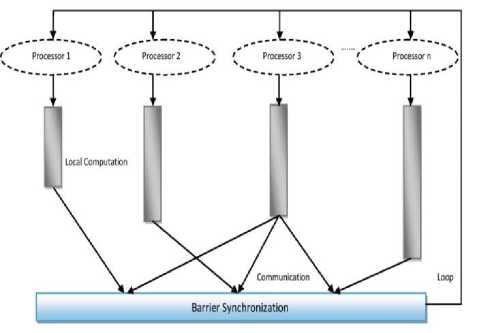
Fig.2. A BSP Superstep

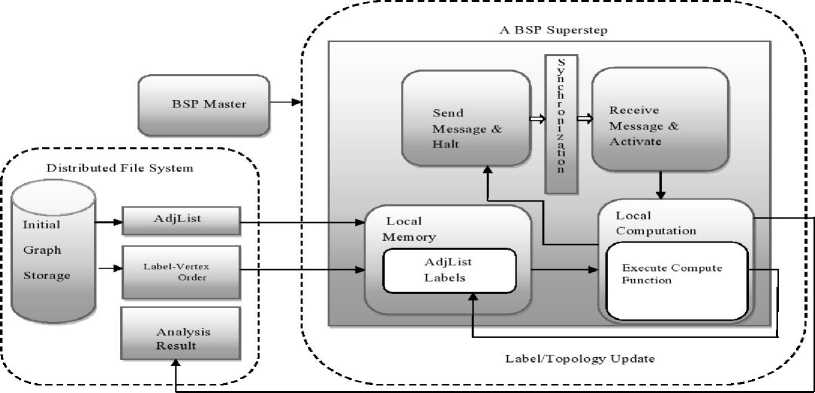
A BSP computation consists of a series of iterations, called supersteps. During a superstep, the system calls a user-defined function at each vertex, in parallel. The function reads messages sent to vertex in superstep S – 1 and send messages to other vertices that will be received at superstep S +1. Within each superstep, the vertex executes compute function in parallel, each executing the same user-defined function that defines the implementation of a given algorithm. A vertex can update its state or that of its outgoing edges, receive messages sent to it in the previous superstep and can send messages to other vertices .The BSP programming model for graph processing is shown in Fig. 3. As the graph structure is kept static on the nodes which perform computation, BSP has only less overhead for data transfers. Moreover main memory based computation in BSP is faster than disk based mechanisms used in MapReduce. If the whole structure of the graph cannot be fit into the main memory of the workers, swapping with disk techniques can be implemented. The features of the two models with respect to graph processing can be summarized in table 2.

Table 2. Features of both approaches in graph processing

	Feature	MapReduce(MR)	BSP
1	Nature of the job	Job with map and reduce functions	Map only job
2	Basic unit of processing	An iteration made up of two MapReduce jobs	A superstep
3	Graph vertex allocation	At each iteration before map	Only once, at the beginning
4	Work allocation among machines	Repeated at every iteration	Fixed at the beginning
5	Set of nodes processed on single machine	Changed before every map	Fixed at the beginning
6	Data about vertex and its neighbors	Transferred before each map	Transferred once before entire processing
7	Memory in use	HDFS and distributed cache	Distributed main memory

Result from Last Superstep

Fig.3. BSP programming model for graph processing

• IV.    Benchmark Algorithm-Triangle Counting

The clustering coefficient of a node in a graph is an important centrality measure which is used in social network analysis can be reduced to the problem of counting triangles. Most of the complex real world networks generate big graphs with millions of vertices and edges in which triangle counting becomes a very computationally intensive task. The basic node iterator algorithm for triangle counting can be performed in two iterations and the MapReduce implementation of node iterator can be done as a chain of two MapReduce jobs. We have selected triangle counting as a benchmark in order to show that along with the iterative nature, there are many other factors which affect the parallelization of graph algorithms.

• A.    Triangle Counting in MapReduce

The MapReduce algorithm used in our experiments is adopted from [2].The algorithm performs triangle counting using a chain of two MapReduce jobs. The first MR job finds the possible paths of length two by processing every node in parallel. The second MR job checks whether there exists a closing edge that completes the triangle and if exists then emits that a triangle is found. The mapper of MRjob1 implements logic to avoid counting triangles more than once and the reducer generates length two paths. The mapper of MRjob2 reads both the input graph and the output from MRjob1 and emits accordingly with a differentiator. The reducer of MRjob2 checks for the closing edge and emits the triangle incident at a vertex. The degree of the vertices can be pre computed and can be used to insist that counting should be done by the nodes which have lesser degree. This may slightly improve the logic but will require one more MapReduce phase and therefore will not make much improvement in execution time.

• B.    Triangle counting in BSP

The communication and memory overhead of the BSP based triangle counting algorithm in the current literature[5] is very high due to large number of message generation and transfers which will affect the BSP execution. We propose an enhanced algorithm which uses the vertex degree information to reduce the communication cost due to message transfers and thereby gains an improved performance. The entire processing can be done using 4 supersteps. In superstep 0 the label of every vertex is updated with the degree of the vertex.In superstep 1 every vertex will forward its label to its adjacent vertices whose degree is either greater than the sender or if the degrees are equal then to the vertices with greater value for the unique identifier. This constraint ensures that a triangle needs to be counted only once and that the majority of the work needs to be done by lower degree vertices. In superstep 2, each vertex will forward the message it received to its adjacent vertices again by following the ordering rule. In superstep 3, each vertex checks whether the identifier mentioned in the message is present in its adjacency list and if present the message will be forwarded to the corresponding vertex. In superstep 4 each vertex counts the number of messages received which will give the number of triangles incident at that vertex.

Algorithm 1 MapReduce algorithm for triangle counting

MRJob1:

• 1:    function map(vertex id a,vertex id b)

• 2:    if(a

• 3:      emit(a,b)

• 4:    end function

• 5:    function reduce(vertex id a, vertex set A : AϵAdj(a))

• 6:   for(m,n) where m,nϵ A do

• 7:     emit(a,(m,n))

• 9    end for

• 8:    end function

MRJob2:

• 1:    function map(Object I,Object K)

• 2:   if I of type a and K of type (m,n)

• 3:     emit((m,n),a)

• 4:   if I of type (m,n) and K of type $

• 5:     emit((m,n),$)

• 6:    end function

• 7:    function reduce(Object I :Iϵ(m,n), Object M: MϵVU {$})

• 8:   If $ϵM then

• 9:    for mϵV ᴖM do

• 10:       emit(m,1)

• 11:     end for

• 12:   end if

• 13:    end function

Algorithm 2 BSP based algorithm for triangle counting

Superstep 0 1:    function compute(vertex v) 2:  order(v) ^ 0 3:    for all u in adjlist(v) 4:     order(v) ^ order(v) +1 5:   end for 6:  labcl(v) ^ ordcr(v) 7:  votetohalt() 8:    end function

Superstep 1 1:    function compute(vertex v) 2:    for all u in adjlist(v) 3:    If(label(v) 4:       sendmessage(adjlist(v), [iden(v),label(v)]) 5:      end if 6:   end for 7:  votetohalt() 8:    end function

Superstep 2

• 1:    function compute(vertex v, message[m₁,m₂..m_k ; k<|v|])

• 2:   for all m in message

• 3:      for all u in adjlist(v)

• 4:       if(label(m)

• 5:         sendmessage(adjlist(v),[iden(m)])

• 6:        end if

• 7:     end for

• 8:   end for

• 9:  votetohalt()

• 10:    end function

Superstep 3 1:    function compute(vertex v, message[m1,m2..mk; k<|v|]) 2:   for all m in message 3:     V t ^ idcn(m) 4:        if V t is in adjlist(v) 5:       sendmessage(V t,[iden(m)]) 6:        end if 7:    end for 8:  votetohalt() 9:    end function

Superstep 4 1:    function compute(vertex v, message[m1,m2..mk;k<|v|]) 2:  (ricount(v) ^ O 3:   for all m in message 4:     tricount(v) ^ tricount(v)-j 5:   end for 6:  labcl(v) ^ tricount(v) 7:  votetohalt() 8:    end function

• V.    Experimental Environment

  The fixed infrastructure used for performance measurements is a cluster of 8 homogeneous computing nodes of dell power edge sc1425 machines with Intel exon processor and 4 GB memory on every node .The multinode cluster is set up in redhat Linux with Hadoop version 1.0.3 and Giraph version 1.1.0 as working platforms. Hadoop version 1.0.3 and Giraph version 1.1.0 are used for MapReduce and BSP implementations respectively. Giraph assumes a master-slave architecture in which the vertices are partitioned and assigned to

workers by the master while workers execute the vertices and communicate with each other. Giraph uses Apache Zookeeper for synchronization and Hadoop for launching BSP workers within mappers. Real graphs from SNAP[10]dataset collection and synthetic graphs generated using graph generators are used for the experiments. We also performed several MapReduce passes to preprocess the graph data. The real datasets from various domains used in the experiments are ca-GrQc, Enron-email, com-DBLP and roadNet-CA. The description of the datasets used are given in table 3.

Table 3. Dataset Description

ca-GrQc email-Enron com-DBLP roadNet-CA Domain Collaboration network communication network collaboration network Road network No. of Nodes 5242 36692 317,080 1,965,206 No. of Edges 14,496 1,83831 1,049,866 2,766,607 Undirected(y/n) Y Y Y Y No. of Triangles 48,260 7,27044 2,224,385 12,0676 ca-GrQC (General Relativity and Quantum Cosmology) collaboration network is taken from SNAP data collection which contains scientific collaborations between papers submitted to General Relativity and Quantum Cosmology category in the e-print arXiv. Enron-email is a communication network which contains email communication within a dataset of half million emails and is made public by the Federal Energy Regulatory Commission. The DBLP  is a  computer science bibliography which contains a comprehensive list of research papers in computer science. The network is build such that two authors are connected if they publish at least one paper together. RoadNet-CA is a road network of California in which intersections and endpoints are represented by nodes and the roads connecting these intersections or road endpoints are represented by undirected edges.

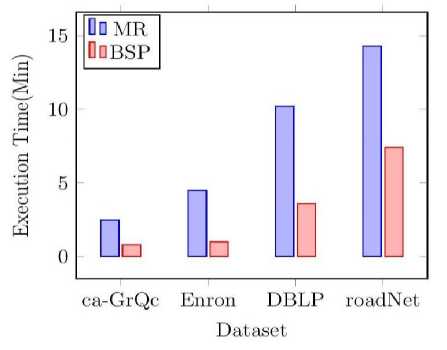
Fig.4. Execution time on 8 node cluster

B. Scalability with respect to graph size

• VI.    Experimental Results

• A. Time of computation with respect to same cluster

Both MapReduce and BSP models were examined by implementing triangle counting algorithm using a fixed cluster of 8 machines. The results obtained from the experiments are shown in Fig. 4.It has noted that BSP can outperform MapReduce to a great extend for all the datasets used in the experiments.

Experiments were conducted to measure the scalability of the platforms using datasets with varying number of edges and by keeping fixed cluster size. Fig.5 shows the experimental results from triangle counting implementation. The execution time increases with the number of edges in both the platforms, but BSP shows a less rate of growth compared to MapReduce. Similar results were obtained by varying the number of vertices of the graph.

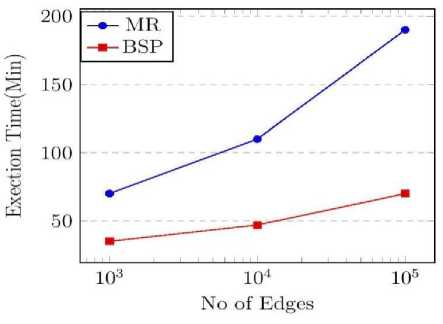
Fig.5. Scalability with respect to number of edges

We also observed that if we increase the size of the graph such that either the graph size or the total messages generated during the algorithm implementation cannot be stored or processed in the main memory of the cluster, the BSP system will crash but MapReduce can continue its work due to the disk storage mechanisms used. But this problem in BSP can be overcome by either increasing cluster size or by using spilling to disk technique which is supported in latest version of Giraph (version 1.1.0) and will slightly increase the execution time.

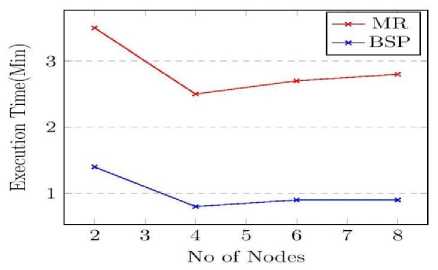
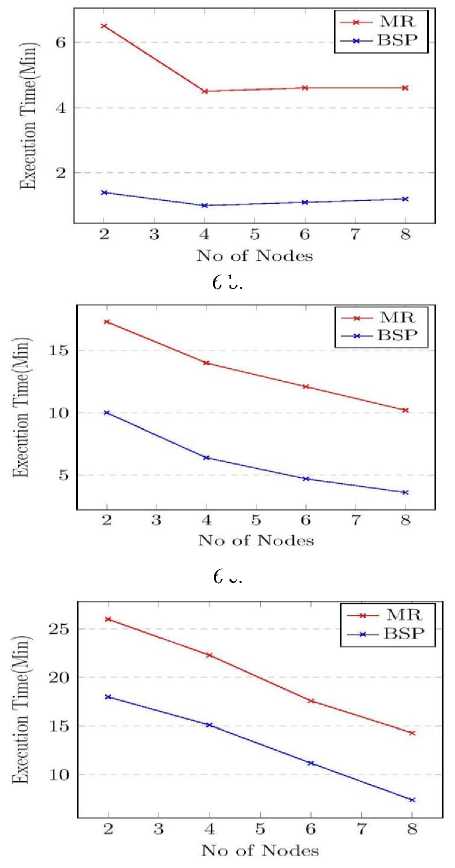
• C. Scalability with respect to Cluster size

The effect of cluster size in the performance is also compared by varying the number of nodes in the cluster. The results are shown in Fig. 6.a-6.d. For smaller datasets like ca-GrQc and email-Enron, it is observed that the execution time converges at a cluster size 4 beyond which advantage of parallel computing will be nullified by the overhead due to network communication. Clearly BSP outperformed MapReduce to a great extent in this section. For roadNet-CA and com-DBLP datasets we used out-ofcore message option in Giraph to avoid crashes in BSP and it is observed that the execution time decreases with the increase in cluster size, but the difference from the MapReduce execution time is reduced. With out-of-core graph/message option, Giraph will keep limited number of vertices/messages in the main memory with remaining on the local disk and swapping is done when needed.

6 a.

6 b.

6 c.

6 d.

Fig.6. Scalability with respect to number of nodes in the cluster for datasets a) ca-GrQc b) email-Enron c) com-DBLP d) roadNet

D. Performance with respect to Structure of the graph

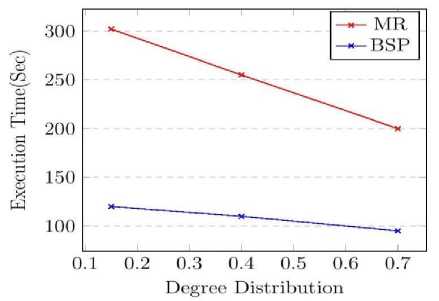
Fig.7. Scalability with respect to graph structure

We generated synthetic random graphs with fixed number of nodes and edges but with varying degree distributions and analyzed the performance of the platforms against the structural properties of the graph.

The results from the experiments are shown in Fig. 7.It is observed that the execution time decreases in both the platforms with the decrease in skewness. This shows that the skewed degree distribution property of scale free graphs is not well handled by both the platforms.

• E.    System Resource Usage

BSP approach requires more memory than MapReduce as the system is designed for in-memory computations. In MapReduce the CPU utilization is high during mapper execution compared to shuffle /sort and reducer executions. In BSP the synchronization phase between the supersteps is the least computationally intensive task. Another important observation is that the skewed degree distribution of the graph will increase the memory utilization and CPU usage in both the platforms. In MapReduce, it is caused due to the fact that 80% of the map and reduce tasks will be completed quickly compared to 20% of the rest of the tasks. In BSP, the synchronization phase between supersteps causes some nodes in the graph to wait for a few nodes with higher degree which makes the same result.

• F.    Communication Overhead

In general, the communication overhead for BSP will be less when compared to MapReduce. But the overall network overhead is found high in BSP for triangle counting as the algorithm involves lot of message transfers but it actually depends upon the algorithm design. In MapReduce, network traffic is observed high at the beginning of each iteration. The allocation strategy of data at different disk blocks in the distributed file system is also a factor which affects the communication overhead in both the systems.

• G.    Granularity in Computations

In parallel computing granularity refers to the fraction of computation cost to the communication cost. The programming model of BSP supports fine grained parallelism as the computation at every vertex is very less and the synchronization between supersteps require frequent communications. MapReduce tend to lean more towards coarse grained parallelism as every map and reduce operations are performed on a collection of vertices which involves more computations at every unit of work.

• H.    Coding Complexity and System Cost

Both MapReduce and BSP algorithms are written in Java using the programming primitives of Hadoop MapReduce execution engine and Giraph BSP engine respectively. A complexity comparison of algorithms used is not included in this work as both systems involves use of both memory and disk and a proper complexity analysis in terms of asymptotic bounds is not possible in this case. Only open source tools, commodity hardware and freely available datasets are used for the experiments with both the models. So both models can be considered as cost effective with respect to data analysis.

• VII.    Discussion

From experiments conducted using datasets of various domains, it is observed that BSP can outperform MapReduce  in graph processing. The  in-memory computation is the main factor behind the improved performance of BSP over MapReduce. Even if the cluster memory is not sufficient for graph storage and processing, modern BSP systems can provide spilling to disk mechanism which even can give better performance than MapReduce. The resource utilization by both the platforms is influenced by the design of the parallel graph algorithms and also by the structure of the graph. Both the platforms are not well suited for handling graphs with skewed degree distributions, which demands efficient graph partitioning techniques for load distribution and balancing to be implemented within the framework.

• VIII.    Conclusion and Future Work

As the size of the real world graphs becomes very large, the need of using parallel algorithms for graph processing has attracted researchers. This works aims at conducting a performance and feature comparison of the parallel computing based Big Data platforms, MapReduce and BSP on graph processing by considering triangle counting as a benchmark problem for study. Experiments with graph datasets of various domains showed that BSP can be a better platform for graph analytics if the cluster is equipped with enough physical memory for graph storage and operations. Latest versions of BSP systems support spilling to disk techniques which can handle memory constraints. BSP can also provide a more natural way of programming with graphs than MapReduce. The structure of the graph remains to be an interesting challenge for both the platforms and can be a good area of research.

The work can be enhanced by including an iterative MapReduce model into the current comparison and also by adding more graph algorithms as benchmarks. A comparison of BSP frameworks, Giraph, GraphLab and Graphx can be another interesting research direction. Parallel algorithm design and implementation for scalable social network analysis using BSP models can also be considered for work in future.