A robust functional minimization technique to protect image details from disturbances

Published Online July 2019 in MECS

During the last decades, imaging activities all over the world have been increasing tremendously due to the huge application of cameras, videos or other imaging instruments in many areas of application. All most in every sectors including medical science, computer vision, satellite imaging, classification or segmentation, motion detection, fraud or intrusion prevention, traffic security or road safety where usages of images are overwhelming. Due to the large volume of image applications, it is an emerging issue how an image can be smoothed while preserving its own and actual properties. Nowadays, it is not an issue how much the imaging equipment or video capturing instrument is efficient; however, the captured images or videos are always found in less or more erroneous condition due to the different disturbances during its transmission or acquisition. A faulty imaging system always hampers image quality by incurring unpredicted noises to the original imaging signals. The erroneous images subsequently lead malfunctioning during image operation or analysis and produce garbage output. Therefore, effective and efficient way of image smoothing, as well as developing a robust technique to remove noise and preserving image properties is appreciative and still challenging for the community of image vision and analysis. In real applications, image smoothing is always a noteworthy issue since its preprocessing is urgent to construct a good quality image. In the real field of image applications, it is observed that the bulk amount of noises is incurred from different known and unknown sources during its capturing phase. Therefore, an attempt to eliminate these impurities from the contaminated images is unquestionably necessary to produce a clean version that would be more useful in any image related operations.

During a plenty of times, many approaches for the purpose have been discovered in scientific literature. However, the image smoothing problems significantly come into the notice are reported in many research articles including local filtering-based image smoothing [1, 2], nonlocal-based methods [3- 6] are also noted in literature. Nonlocal wavelet-based method [7, 8], nonlocal-based sparse coding strategy [9], nonlocal low-rank [10], the sparse representation techniques [11], shearlet-based model [12], curvelet-based method [13], dictionary-based approaches [14, 15], soft-thresholding method [16], image deblurring technique using regularization [17], the radial basis function (RBF)-based method [18] and image retrieval with color and angle representation [19] are also remarkable in applications. However, many other methods based on variation and partial differential equation (PDE) have been proposed widely since variational calculus come out recently as a powerful tool for image-smoothing and model solutions. Moreover, the solution of the models can ensure image smoothness and details preservation abilities, those abilities are also reported as in the PDE-based methods [20, 22]. Similarly, energy minimization or variationalbased approaches such as [23- 25, 27-29] are widely using in image enhancement problems. The nonconvex-based smoothing approaches such as [30-33] can also preserve image details. However, a total variation (TV)-based scheme known as ROF technique [34] and the Chamboll's method [35] in the form of minimization problems are famous for regularizing noisy images. An efficient impulse noise removal approach is described by Yu et al. [36]. In this approach, the time for denoising process is relatively less as their algorithm iteratively implemented, however the performance is not good enough. A fast minimization method for image restoration is proposed by Nikolova et. al. [31]. They used nonconvex non-smooth regularization on L2 norm to show the advantages over convex regularization with edges preservation ability. However, the technique is computationally inefficient since it requires a nonconvex smoothing. In the same direction, Zuo et al. [32] proposed an adaptive nonconvex non-smooth (ANCNS) regularization approach to show better restoration of image edges, however it incurred time penalty as it requires a nonconvex minimization. In [37], Sutour et al. proposed a new method with TV regularizer and nonlocal means scheme to reduce the residual noise but the method still unknown to deal with other types of regularizers except TV-based regularizer. In [26], Liu et al. proposed a higher order total variational (HDTV) model as the form of weighted L1-L2 mixed norms for image enhancement but the convergence of HDTV is still unknown in this work. In [21], Wang et al. proposed a nonlinear fourth-order PDE based denoising method by approximating energy to preserve textures only for additive noise but the performance still unknown for other types of noises.

The existing literature reviews reveal many imageenhancement techniques those have been introduced for endeavoring image quality. However, intensive analysis is still enduring toward superior way of preserving image details and noise removal simultaneously. Although some of the existing techniques perform less or more effective in some context, but still there are many techniques are not good enough. For example, the TV-based image enhancement technique [34] uses convex energy to protect image properties. However, the high isotropic polishing phenomena hamper some important image details. To defeat this problem, a nonconvex way of enhancement is proposed in [27, 30] which ensure the ability of details protection and noise elimination. However, it is much slower method and cannot guarantee unique solution. The technique also recognizes noises as image element in homogeneous regions. As a result, a new technique is reasonably necessary to remove noise while keeping the original image properties. Therefore, the objective of this work is to introduce a robust functional minimizing technique for better image smoothing performance while keeping the actual image details.

Rest of the paper is separated as follows: Section II describes the details of proposed technique including the basic image enhancement consequences. The Section III shows experimental studies. Performance assessment is reported in Section IV. Finally, Section V concludes this paper.

• II.    Details of Proposed Technique

During the last decades, imaging activities all over the world have been increasing tremendously due to the huge application of cameras, videos or other imaging instruments in many areas of application. Generally, faulty imaging systems, environmental problems or distortions during capturing process often degrade image quality by incurring enormous noises. Eliminating these susceptible artifacts from the original images is the vital requirement for smoothing and recovering the image details. For the purpose, the key concern in image smoothing is to protect details while eliminating noise or other vulnerable objects. A good balance between noise elimination and details protection is extremely necessary for constructing high quality images. Therefore, we attempt to investigate the existing limitations and aim towards a robust way of image quality improvement using a new methodology as describe in the subsequent section.

Noise reduction simply refers to the way of eliminating disturbance-artifacts from the actual images. Let p_ij is the real or authentic image where p : Q c R ² ^ R and Q is image domain, qj is the noisy image with Gaussian noise n j , then mathematically, the degraded image can model as Eq. (1):

q ij = pij + 'i (1)

The reconstruction of pij from qij here is the ultimate objective. An approximation to pij can be ensure from the following minimization problem (2):

min LI qij - pij\ (2)

To manage the ill-posed issue [38] in minimization, an image regularization or smoothing term as in Eq. (3) is essential with the original signal to resolve the minimization problems (2):

min <  P

L (P) = F (P) =£1 qij - pij |2 dx + ■£'■pij f dx

In (3), the first and second terms treat as fidelity and the regularizer or smoothing term respectively. In TVbased image restoration [34], the fidelity and regularization terms describes the noise levels and image smoothness respectively. In practice, the image enhancement performance largely depends on smoothing terms. In (3) second term regularizes the images where X is the balancing parameter. The dilemma (3) can be flourished by Euler-Lagrange Equation as (4) which pledge a unique solution:

^A xpij = pi + 1, j ^- pij ^{and A} ypij = pi , j + 1 ^- pij

py - q ij - X^Pij = 0              (4)

with boundary conditions:

—p = 0 on Q (D indicates the outward normal to Q) 5D and the necessary mathematical propositions to solve the problems are discussed below:

The Gradient of p refers to V p as the gradient vector, which can be defined as:

Although TV-based method can enhance images, however it eliminates some valuable image details simultaneously due to its polishing effects. Thus, an alternative regularizing term for the quality solution is introduced in [27, 30] and illustrate the efficiency of this nonconvex technique as (6):

I n qj  p ^ij

1^{2 dx +} Jn 4 pij 6

dx

Vp(x) =

pp.....6p L r

(ax1     axn)

в г

The function ^(r) = —— where в is a positive '       1 + вг parameter. The vital advantage of this nonconvex technique (6) is the ability of details preservation but alarming issues are uncertainty of unique solution and allow noise as original detail particularly in boundary regions. As a remedy, we examine the respective limitations and propose a robust functional minimizing technique that can be modeled as in the following form of functional (7):

The divergence on V p as the following terminology:

div (Vp) = £ "p- i=1 ОXi

The Laplace p ( A p ) can be expressed as:

^{L (} p ) = 2 f _Ql qij - pij I" ^{dx + 5} I_Q ^V pj l ^dx

+ (1 - 5)In ^(Vpij I)dx

n ²

Ap = div (Vp) =1^4 i=1 dX2

The TV-based technique [34] utilizes L norm of Vp^ ij in (4) instead of L2 in (3), and it express as in the form of Eq. (5):

J_n| qj   ^p j

12 dx+xJq^j

dx

where the term

£|^{V p} ij\  in ⁽⁵⁾

stands for the total

The functional (7) can ensure the better noise reduction and edge protection ability simultaneously since it inherits the benefits of both TV and nonconvex-based techniques by assigning 5 = 1 and 5 = 0 respectively. The use of discrete variational principle to the discrete functional is necessary to solve the minimization problem. The appropriate parameters and weight estimation always influence the better trade-off during image smoothing process. However, the direct solution of (7) is obscured due to nonconvex functional. Therefore, we need to handle the image regularizer i.e. handling smoothing term by iteratively reweighted method as (8):

4pijЙ = [ 1+|ад] Apij\ = ^hpj (8)

variation (TV) of pij image. For implementation, we need to introduce a discrete form of TV-based approach as in the following way. If the minimization problem of discrete functional F then:

min F = min E L ( pij - Qj ) i , j

= ^min i E j ^X j ^{- q} ij Г + ^V j

where ^pij-1 =|AxFij ) +(AyFij )

1+5

In (8), we define a robust weight щ as: ----------

1 + 5 | V pjj | where 5 is the arbitrary positive parameter ranges[0.01, 0.09] . For eliminating noise and protecting image details to construct visually high quality image, our robust technique (8) can be implemented by solving the following functional minimization problem (9):

.   2 I n q ^- p^{2 dx}

min ■

p

+ J (5 + (1 - 5)щ) |Vp|dx

As у is given, the above Eq. (9) is convex and unique solution is confirmed. The Chambolle’s projection algorithm [35] is used to attain the solution of the functional minimization (9), which is specified as Eq. (10):

Pi = q i - Я div z i (10)

where div z is the divergence (div) of the vector z : Q^^x^ expresses a vector function and z i e^ n is selected by a fixed point principle : given z ⁰ = 0 is a first estimate and suppose time-step = ст , then we iterate the scheme (11) for the solutions:

indicator SSIM is used for image quality comparisons between proposed and existing techniques. There are huge numbers of reference images have been used for performance assessment in this domain. However, we use several images for experimental analysis and quality evaluation as it facilitates to minimize the length of the paper, it does not mean the limitation of diversified using of other images.

The SSIM index is calculated based on the similarity between the clean image and restored image. The vale between the range 0 and 1 is used as the SSIM index. The high value of SSIM index signifies more structure similarity between the original image and resorted image. The SSIM is measured as Eq. (12) based on clean image p and reconstructed image p :

z t ^{+ 1}

zt + oV(div zt - q?)

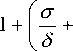
( 1 — 8 ) y|

div z t - q i

SSIM =

(2врвр + 61 )(2фр + 62)

(ep + Эр + 61 ) (фр + фр + 62 )

• III.    Experimental Studies

  To verify the effectiveness of diverse image enhancement techniques, the experimental details are presented in this section. Matlab 2017a on a computer configured with core-i5 and 3.20 GHz is used for implementing the algorithms. For experimental setup, the parameters Я , 8 , ст and § are required to be initialized before execute the experiments. The standardize image size is [ 256 x 256 ] and range of intensity is [ 1,256 ] respectively. The controlling parameter Я is equivalent to the noise level and 8 is selected from a fixed range [ 0, 0.6 ] as in [27, 30], however we choose 8 for any values from the range [ 0,1 ] . In experiment, the parameters Я and 8 are for the role of controlling the smoothness. We set ст for any random value from the ranges [ 0 <  ст < 1 ] . The value of § is determined from the random ranges [ 0.01, 0.09 ] . To assess the performance, a set of reference clean images in (a) and their corresponding noisy images in (b) of Fig.1 are used respectively. The parameter N is connected to the standard deviation of the noise q . To condense the pages of the paper, the noise parameters N is fixed from the set { 10, 20, 30, 40 } where higher N specify stronger noise intensity. However, any intervals of noise intensity can be tested for the experiments.

• IV.    Performance Assesments

The performance comparisons can be validated by both visual and numerical improvements. Based on original and restored images, signal to noise ratio (SNR), peak signal to noise ratio (PSNR) and structural similarity (SSIM) can be the evaluation indicators. The qualitative where вр and ф are the mean values of the clean and restored image, respectively. Similarly, фр and ф are the variance values of the clean and restored image, respectively. ф- is the covariance of images p and p ; two variables 6 and 6 are assigned with a weak denominator to stabilize the division.

We exhibit image smoothing results including image details preservation ability in (c)–(e) of Fig.1 for visual assessment, and the results in Table 1 for quantitative assessment respectively. From the Table 1, it is observed that our proposed technique on average attain higher SSIM values than the other traditional techniques. Evaluating the results in (c)–(e) of Fig.1, it can make sure that the proposed technique can wipe out much noise and protect image true details more competently, particularly in edge regions. For example, the smoothed results in (c) of Fig.1 are generated by TV-based technique still take hold of visible noise and produce over enhancement while iteration increased. The images by nonconvex-based technique are revealed in (d) of Fig.1. The results show that some image details are also removed in (d) and over-smoothed in (c) than the results exposed in (e) of Fig.1.

For more precise comparisons, we enlarged restored images in (c)-(e) of Fig.1. From the magnified observation, the restored images by proposed technique in (e) make sure the visually better quality images than the same images restored by TV-based and nonconvex-based smoothing technique as shown (c) and (d) in Fig.1 respectively. In (e) of Fig.1, the restored boundary objects or edges are much clean and sharper with more scene details. However, images (c) still contain noises and oversmoothed the boundary areas; and images (d) restore noises with image details in homogeneous regions. It indicates that the proposed technique simultaneously can remove more noise in homogeneous regions and preserve edge details efficiently than other methods.

a

b

c

d

e

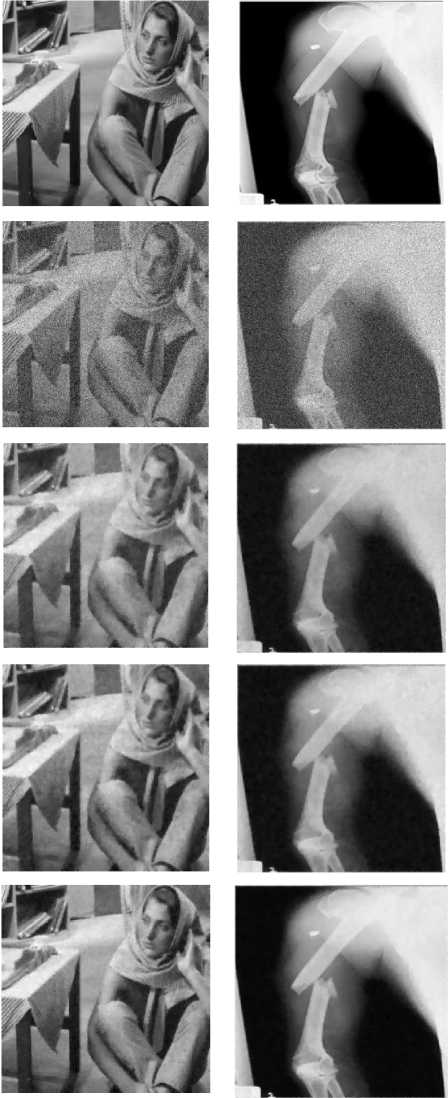
Fig.1. Performance comparisons: a original image, b noised image with N = 30, c TV-based technique d Nonconvex-based technique and e proposed technique

Table 1. SSIM comparisons and performance evaluation for different techniques

Name	N	Noisy Image	TV-based (5)	Nonconvex-based (6)	Proposed
	10	0.611	0.829	0.854	0.867
House	20	0.501	0.706	0.738	0.743
	30	0.409	0.635	0.663	0.671
	40	0.365	0.593	0.612	0.622
	10	0.631	0.899	0.919	0.933
	20	0.559	0.839	0.863	0.871
Peppers	30	0.514	0.794	0.817	0.830
	40	0.466	0.756	0.779	0.798
	10	0.663	0.896	0.920	0.927
	20	0.591	0.821	0.846	0.853
Butterfly	30	0.497	0.761	0.785	0.792
	40	0.399	0.713	0.736	0.741
	10	0.626	0.879	0.894	0.907
Cat	20	0.538	0.797	0.817	0.831
	30	0.478	0.736	0.760	0.775
	40	0.397	0.698	0.718	0.722
	10	0.619	0.887	0.908	0.925
Flower	20	0.583	0.833	0.858	0.865
	30	0.506	0.789	0.812	0.821
	40	0.498	0.754	0.774	0.791
	10	0.632	0.869	0.884	0.891
Barbara	20	0.528	0.792	0.809	0.817
	30	0.493	0.741	0.760	0.769
	40	0.391	0.701	0.723	0.734
	10	0.679	0.934	0.959	0.975
Carpet	20	0.586	0.848	0.876	0.919
	30	0.491	0.752	0.789	0.853
	40	0.397	0.693	0.714	0.793
	10	0.617	0.886	0.896	0.906
Lake	20	0.481	0.784	0.808	0.819
	30	0.402	0.719	0.741	0.755
	40	0.376	0.662	0.688	0.701
	10	0.611	0.882	0.890	0.917
	20	0.509	0.791	0.806	0.835
HandXray	30	0.496	0.727	0.748	0.788
	40	0.394	0.683	0.707	0.749

* Bold indicates the corresponding maximum SSIM values

V. Conclution

Acknowledgment

In this paper, a robust functional minimization technique is presented for image enhancement while protecting the actual image details from the environmental disturbances. An efficient algorithm has been introduced and implemented under variational framework for finding the robust solutions. Moreover, the key challenges in order to edge and image details protection from high polishing affects have been addressed and tackled efficiently in cooperation with designated smoothing term. The performance of the proposed technique is also tested and verified by a number of sample experiments. The visual and quantitative results ensured the efficiency of the proposed technique in order to protect valuable image details while eliminating noise in homogeneous or edge regions than other methods.

This work was supported in part by the National Natural Science Foundation of China under Grants 61402290, 61472257, 61772343 and 61379030; in part by the Foundation for Distinguished Young Talents in Higher Education of Guangdong, China, under Grant 2014KQNCX134; in part by the Natural Science Foundation of Guangdong, China, under Grant 1714050003822; and in part by the Science Foundation of Shenzhen Science Technology and Innovation Commission, Grant JCYJ20160331114526190, China.