A Robust Non-Blind Watermarking Technique for Color Video Based on Combined DWT-DFT Transforms and SVD Technique

Published Online August 2014 in MECS

A digital watermark is a kind of marker covertly embedded in a noise-tolerant signal such as audio or image or video data. It is typically used to identify ownership of the copyright of such signal. Watermarking is the process of hiding digital information in a signal such that when a user access it and claims that he is the owner of the content, he can be easily caught by extracting the digital information from the signal and finally the original owner claiming the ownership rights of the signal. Digital watermarks may be used to verify the authenticity or integrity of the signal or to show the identity of its owners. It is prominently used for tracing copyright infringements and for banknote authentication. Nowadays digital watermarking has many applications such as broadcast monitoring, owner identification, proof of ownership, transaction tracking, content authentication, copy control, device control, ECG, X-ray, EEG, and file reconstruction.

Watermark can be embedded in both spatial domain and frequency domain, but spatial domain is less robust to attacks when compared to frequency domain. In frequency domain image is transformed using DCT, DWT, DFT and the watermark is embedded onto frequency coefficients of transformed image. Invisible watermarking holds well in frequency domain since watermark is embedded onto frequency coefficients of transformed image which is less sensitive to human eye. The discrete wavelet transform has a huge number of applications in science, engineering, and mathematics and computer science. Most notably, it is used for signal coding, to represent a discrete signal in a more redundant form, often as a preconditioning for data compression.

Different frequency domain watermarking techniques have been proposed. Reference [1], [2], [3], [4], [5] proposed DFT based watermarking technique wherein watermark is embedded onto phase of DFT. Discrete Fourier transform of an image is complex valued leading to real and phase components and they found out that phase component is more robust to tampering. Reference [6], [7], [8], [9], [10] proposed a unique combination of DWT-DFT-SVD based watermarking technique and obtained promising values of Peak Signal to Noise Ratio (PSNR) and Normalized Correlation (NC). Reference [11], [12], [13], [14] proposed various watermarking technique of videos. Reference [15] proposed DWT-SVD based watermarking technique using scrambling algorithm for watermark encryption in YCbCr color space. Reference [16], [17], [18], [19] proposed watermarking technique in YUV color space along with other transforms like DWT, DFT and DCT.

The paper proposes DWT-DFT-SVD based watermarking technique using Arnold transform for watermark encryption in YCbCr color space. Fibonacci series has been used for selection of frames.

The rest of the paper is organized as follows: - Section II describes the fundamental concepts in brief used in the process. Section III includes proposed watermarking scheme for embedding and extraction. Section IV shows the experimental results of proposed scheme and Section V concludes the proposed paper.

II.  Fundamental Concepts

A. YCbCr color system

YCbCr is family of color spaces used as a part of color image pipeline in video and digital photography systems. Y is the luma component and Cb and Cr are the bluedifference and red-difference chroma components. Since the native RGB format has lot of redundant values, conversion to YCbCr color space makes it more efficient. Conversion from RGB to YCbCr can be done by the following method.

"Y"

Cb Ст

' 0.299

-0.169

0.500

0.587

-0.331

-0.419

0.114'

0.500

-0.081

"R"

G В

B. DWT-Discrete Wavelet Transform

Discrete wavelet transform (DWT) is any wavelet transform for which the wavelets are discretely sampled. As with other wavelet transforms, a key advantage it has over Fourier transforms is temporal resolution and it is robust to compression: it captures both frequency and location information (location in time). Single level 2 dimensional DWT decomposes the image into LL, LH, HL, and HH frequency bands named according to the filter (high-pass or low-pass) applied in horizontal and vertical direction. Fig. 1 shows the four components of 2D DWT transformed image. The LL sub-band contains much details of an image when compared to LH, HL and HH sub-bands.

C. DFT-Discrete Fourier Transform

M-l N-l

H^v) ^_N^ ^F^,^^W^+^) ₍₃₎ u=O u=O

The Fourier Transform is an important image processing tool which is used to decompose an image into its sine and cosine components. The output of the transformation represents the image in the Fourier or frequenc y domain, while the input image is the spatial domain equivalent. In the Fourier domain image, each point represents a particular frequency contained in the spatial domain image.

The Fourier Transform is used in a wide range of applications, such as image analysis, image filtering, image reconstruction and image compression.

The DFT is the sampled Fourier Transform and therefore does not contain all frequencies forming an image, but only a set of samples which is large enough to fully describe the spatial domain image. The number of frequencies corresponds to the number of pixels in the spatial domain image that is the image in the spatial and Fourier domain is of the same size. Discrete Fourier transform transforms an image from spatial domain to frequency domain. 2D DFT of an image is complex valued which can be represented in terms of magnitude and phase components. DFT helps in noise removal and it is robust to several attacks like JPEG compression, image sharpening, Gaussian noise etc.

• D.    SVD-Singular value decomposition

Singular value decomposition of an image (A) is obtained by

A=USVT                                 (4)

SVD is a decomposition technique which decomposes the image into U, S and V matrices. S matrix is a diagonal matrix of same dimension as image, with nonnegative diagonal elements in decreasing order, and unitary matrices U and V. Singular values of an image is robust to addition of small perturbations.

• E.    Arnold Transform

Arnold transform of an image f(x,y) of size NxN pixels is given as

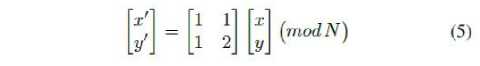
The 2-D DFT of an image f(x,y) of size M x N pixels, denoted by F(u,v), is given as

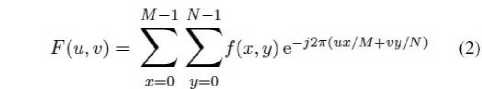
The inverse discrete Fourier transform (IDFT) is given by

Arnold transform is used in watermark preprocessing for scrambling the watermark thereby providing the secondary security even when the intruder extracts the watermark. Watermark can be encrypted to a certain level

based on the user requirements such that at the time of extraction one should know the key value of the number of iterations that have been performed on the watermark.

• III.    Proposed Algorithm

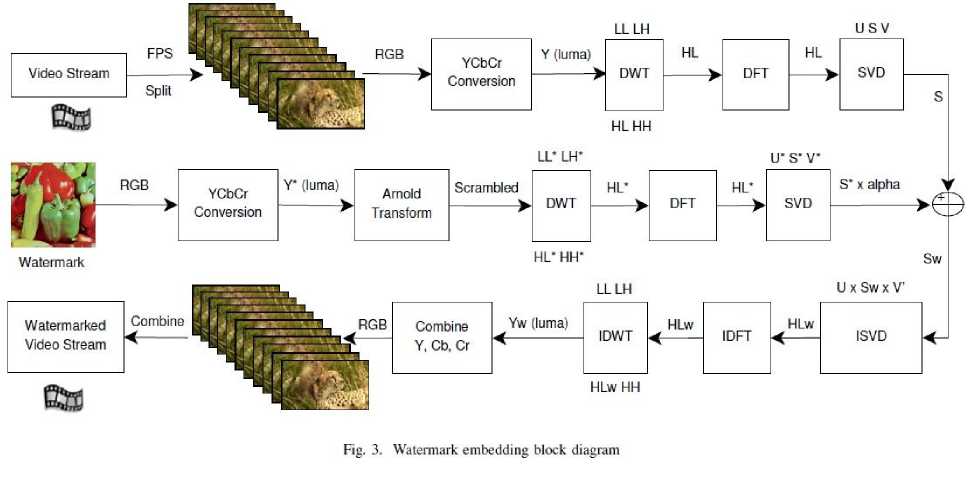
The robustness of the algorithm is enhanced by combining the properties of DWT, DFT, SVD and Arnold Transform. DFT is robust to shift invariance, Gaussian noise, image sharpening, JPEG compression and helps in noise removal. Embedding watermark in LH, HL and HH helps us to increase the robustness of watermark and there will be no impact on image quality. Singular values are very stable and they can withstand smaller perturbations. Frames are selected based on Fibonacci series thereby maintaining the quality of watermarked video and enhancing the security. Arnold transform is applied in watermark preprocessing stage to scramble the meaningful watermark into meaningless watermark, as a secondary security for extracted watermark. The proposed algorithm is divided into 2 stages, watermark embedding and watermark extraction respectively.

• A.    Watermark Embedding

Figure 3 shows the block diagram of watermark embedding stage.

• •    Frames are obtained from the host video based on Fibonacci series and are converted from RGB to YCbCr color space. Here Y component is chosen to embed the watermark.

• •    Single level two dimensional discrete wavelet transform (HAAR wavelet) is applied on the luma component to give 4 sub-bands LL, LH, HL and HH. Out of the entire four components HL component is taken.

• •    DFT is applied to HL* component using Eq. [2] to obtain Fourier transformed HL* component which is a complex valued.

• •    SVD is applied on the resultant component to obtain U*, S* and V* matrices.

A = U*SW*^T            (7)

• •    Embed the singular values of watermark onto singular values of all the frames. Number of singular values to be embedded to each frame is nearly equal wherein α scaling factor determines the strength of watermark.

Sw = S + aS*             (8)

• •    HLw component is obtained by applying inverse SVD for U, Sw and V matrices.

• •    Inverse DFT is applied by using magnitude and phase components to get untransformed HLw.

• •    Inverse discrete wavelet transform is applied to LL, LH, HLw and HH to obtain watermarked Yw luma component.

• •    Yw component is concatenated with Cb and Cr components and converted back to RGB format.

• Then the watermarked frames are combined with        stream.

unselected frames to obtain watermarked video

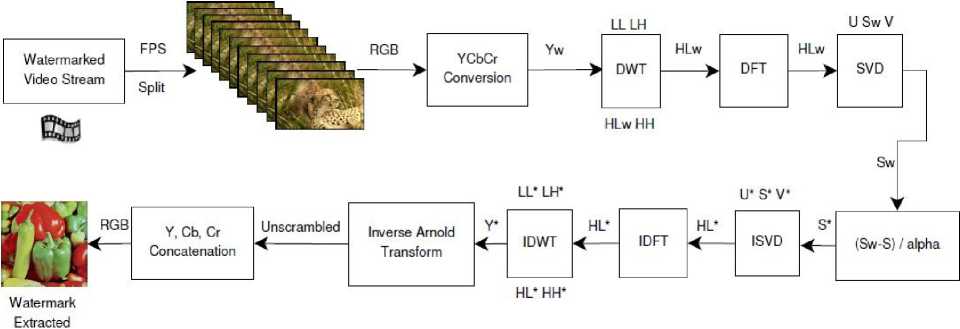
Fig. 4. Watermark extraction block diagram

• B.    Watermark Extraction

Figure 4 shows the block diagram of watermark embedding stage.

• •    Frames are obtained from watermarked video based on Fibonacci series and are converted from RGB to YCbCr color space. Then Yw component is chosen to extract the watermark.

• •    Single level two dimensional discrete wavelet transform (HAAR wavelet) is applied on the luma component to give 4 sub-bands LL, LH, HLw and HH. Out of the entire four components HLw component is taken.

• •    DFT is applied to HLw component using Eq.[2]

• •    Then SVD is applied on the resulting DFT transformed HLw component to give finally an array of U, Sw and V matrices considering the selected frames of video.

Лш = USwV^T           (9)

• •    Singular matrix (S*) of watermark is obtained by the following equation

• IV. Analysis of proposed algorithm and

EXPERIMENTAL RESULTS

Evaluation of algorithm is done using matlab. Videos were chosen randomly from the internet. Color watermark of size 512 x 512 have been chosen. Videos sequences were of the resolution 720 x 1280 uncompressed .avi format. Frames were selected and embedded according the proposed algorithm. Screen shots of frames are shown in the figure 5.

Fig. 5. Top to bottom ‘Cheetah’, ‘Olympics’, ‘Cricket’ [1st col.J Original frames [2nd col] Watermarked frames

To check the integrity of video, peak-signal-to-noise ratio (PSNR) is calculated. PSNR depends on MSE. Mean Squared Error (MSE) of an estimator is the difference between values implied by an estimator and the true values of the quantity being estimated.

MSE =

E [/i(m. n) - 1з(т,n]² M x N

(H)

M,N where I1 and I2 are the watermarked and host image components.

Peak Signal-to-Noise Ratio (PSNR) is the ratio between the maximum possible power of a signal and the power of corrupting noise that affects the fidelity of its representation and it is given by Eq. [12].where M and N are rows and columns of an image.

PSNR = lOlogio

R2 \

MSE J

where R is the maximum fluctuation in the input image data. Normalized correlation (NC) determines the similarity between the original watermark and the extracted watermark and is given by C(X, Y)

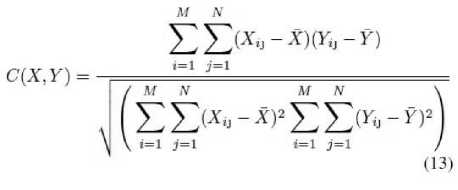
PSNR values has been calculated for variety of videos and the values obtained from 30 frames of ‘Cheetah video’ based on Fibonacci series with α = 0.3 is listed in the below table.

Table i

Frame number	PSNR dB
i	50.4969
2	53.1353
3	54.4479
5	58.3537
8	62.6430
13	71.4923
21	97.7762

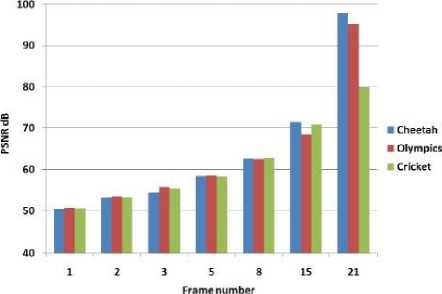
Fig. 6. PSNR comparison wth frames of other videos

We can clearly observe the PSNR rise from frame to frame from the below graph which clearly describes the property of Singular value decomposition technique. In the below graph comparison between PSNR values of 3 videos ‘Cheetah’, ‘Olympics’ and ‘Cricket’ versus frame number is shown.

The robustness of the algorithm is tested by applying various attacks on the video and this may be intentional or unintentional. Salt and pepper noise, rotation, cropping, histogram equalization, image sharpening, Gaussian noise has been applied and we have obtained promising values of NC and PSNR. The α, scaling factor is varied from 0.1 to 1. The threshold level for detection of watermark in compression attacks, motion blur, image sharpening varies from 0.1 to 10 whereas other attacks are limited to 1. PSNR value is still greater than 30 dB when α varies from 1 to 10. Various attacks on proposed algorithm and obtained NC value in comparison with [15]

is mentioned in Table II

Fig, 7. Different attacks on ‘Olympics’ frame

Table 11

Attacks	NC (proposed)	NC (as in /15/)
Salt and pepper, 0.25	0.9803	0.8724
Rotation, 10°	0.9377	undone
Crop (100 xlOO]	0.9997	undone
Histogram equ.	0.9601	undone
Image sharp., [3 3]	0.8943	undone
Median filter	0.9662	0.9561
Gaussian 0, 0.001	0.997	0.6048
Speckle, 0.004	0.9998	0.6562
Motion bluer	0.884	0.9049
JPEG comp., 70	0.8974	0.8938
MJPEG comp., 80	0.8923	0.7346
MPEG comp., 85	0.8887	0.6042
H.264 comp., 80	0.884	0.6505

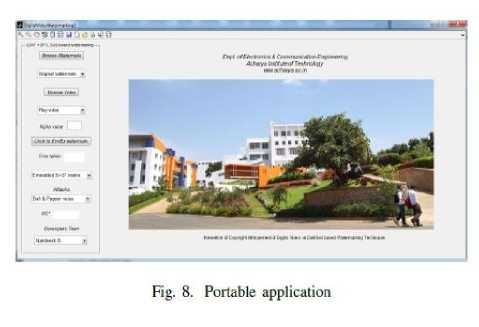
Finally a portable application .exe was built using deploy tool in matlab which serves as a good watermarking software for protection of videos. It takes around 25 seconds to embed and extract watermark image for a video length of 1 second. Here we have taken the videos of resolution 720 x 1280 and a color watermark of size 512 x 512. The application holds good for further research and tabulation since it involves step by step procedure of watermarking. The application is portable and it comes with inbuilt MCR installer package for matlab compiler.

• V.  Conclusion

The proposed algorithm is frame adaptive due to the use of Fibonacci series for frame selection. Here the color watermark is chosen instead of binary image, which is embedded onto High Definition (HD) videos. A portable application is built to make it available for users which serve as a good watermarking software for present day videos. The code can be further extended by converting it into Verilog file using HDL code generator in matlab [21] for hardware implementation. Here the user has to record videos, store them in computer hard disk and then by using the application software, we can embed and extract watermark. PSNR and NC values obtained are compared with [15] and it is found to be better than the algorithm proposed by [13], [14], [15]. DWT-DFT-SVD is a novel algorithm which sustains both geometric and nongeometric attacks.