A Survey on Speech Enhancement Methodologies

Published Online December 2016 in MECS

In human communication speech signal adversely affect by additive background noise and the speech may be degraded. The degraded speech is uncomfortable for human listening and hence the degraded speech must be processed. In speech communication system generally noise is reduced at far-end to improve the quality and at near-end speech modification is done to improve the Intelligibility. Thus speech enhancing/processing aims to improve quality of the speech and/or intelligibility of the speech. To simplify speech enhancement problem necessary assumptions about the nature of noise signal must be considered. Generally noise can be assumed as additive, stationary noise. Over the years researchers developed significant approaches to enhance the corrupted speech and obtained satisfactory improvements under high SNR conditions. Conventional algorithms [1-3] like spectral subtraction, wiener filtering, and subspace approach enhances the corrupted speech and poses the limitations like musical noise. In the process of enhancing, the enhancers attenuate some components of speech and results in intelligibility reduction [3], i.e., if quality are achieved using some methodology there is effect on intelligibility due to processing. Similarly the improvement in intelligibility poses reduction in quality of speech. Hence techniques like processing in modulation domain [4] came in to picture for trade-off between intelligibility and quality [3].

The foremost thing that has to know is what causes the speech to degrade. The degradation may cause due to unnoticeable background noise, degradation results from multiple reflections, [3] and using inappropriate gain. The papers [1-5] provides methodologies on how to enhance the speech when speech is degraded by additive back ground noise, as it has many useful applications in daily life like using mobile in noise environments like offices, cafeteria, busy streets and web applications like Skype, G-talk and sending commands from cockpit of aero plane to ground. To overcome this, many speech enhancement techniques are using noise estimation as its first step [1-2]. Noise estimation can be done mostly in spectral domain like spectral magnitudes, spectral powers. Another approach is using voice activity detector. Voice Activity Detector (VAD) estimates the noise during speech pauses and averages the signal power during all these intervals. Also one important thing while processing the speech in frequency domain is that the processing is done by dividing the speech in to overlapping frames using Hanning / Hamming window and then Short-Time Fourier Transform (STFT) is applied. This step is necessary as speech itself is non-stationary and the transform techniques work only for stationary signals. To apply signal processing techniques the speech is considered to be short time stationary [6] and hence framing must be done. But, some speech enhancement techniques like [3] Adaptive filters, comb filters, kalman filters are processed in time domain. In such case methods applied directly on speech signal itself. The main goal of speech enhancement is either to improve quality or intelligibility or both, that depends on the type of application. For hearing impaired listeners, the main criterion is intelligibility improvement. This can be done by frequency compression and bandwidth expansion. That is why noise reduction can be seen as speech restoration and speech enhancement. In speech restoration, the degraded speech can be restored as original speech where as in speech enhancement it tries the processed signal to be better than unprocessed signal. Thus both terms can be used interchangeably. Estimators using Gaussian and Super-Gaussian prior are developed for better noise reduction [7-14]. As the research is going on, researchers used the perceptual [3, 6] properties of human ear like masking of inaudible components and are successful in obtaining improved results. Supervised methods [15-19] uses training of noise and speech samples and hence no further requirement of VAD calculation and hence obtain improved results. Up to some decades, researchers process the amplitudes of noisy speech where as noisy phase is being unprocessed, as human air is insensitive to phase information. Later on researchers find that phase information is useful [19-23] under low SNR cases. Now researchers shown that, the performance of the speech enhancement will improve by processing the noisy signal phase along with the noisy Amplitudes.

The paper is organized as follows: Section II gives single channel speech enhancement methodologies; Section III discusses the transform domain approaches, Section IV provides decomposition techniques like NMF, Modeling methods using HMM and also provides the significance of phase processing. Section V provides the challenges and opportunities in single channel speech enhancement methodologies. Section VI gives conclusion.

• II.    S INGLE C HANNEL S PEECH E NHANCEMENT M ETHODOLOGIES

3.1) Wiener Filter (linear Estimator) 3.2) Non linear Estimators (For Super Gaussian priors)

Single channel speech enhancement problem mainly deals with the applications where a single microphone is used for recording purpose such as mobile telephony. These techniques provide improvement in the quality of degraded speech. Basically all the methods classify into two categories, one is supervised methods and the others are unsupervised. In supervised methods like NMF, HMM, noise and speech are modeled and parameters are obtained using training samples [16]. Whereas in unsupervised methods like transform domain approaches given in Fig. 1, Wiener filter, Kalman filter and estimators using Super-Gaussian without knowing prior information about speaker identity and noise, processing is done [13]. Supervised methods do not require the calculation of Noise Power Spectral Density (PSD), which is one of the difficult tasks in speech enhancement. For better understanding of developments in speech enhancement methods, they are classified as shown in Fig.1. Generally frequency domain processing [3] is easy and more understandable and hence transform domain methodologies play predominant role. Classification of speech enhancement methodologies are given in Fig.1

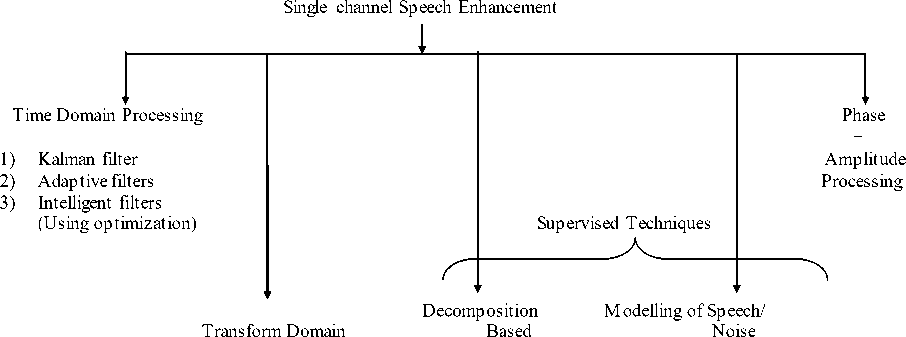
1)  Spectral Subtraction            1) NMF

2)  Wavelet Transform

3) Stochastic Estimation

a) MMSE

b) MMSE-LSA

c) MAP

d) ML

4) Super Gaussian Estimates ( + STFT phase)

5) Modulation Domain

1) HMM

2) GMM

Fig.1. Speech Enhancement Methodologies

• III.    T RANSFORM D OMAIN A PPROACHES

In transform domain approaches, signal is converted into frequency domain and processing is done on DFT coefficients/Wavelet coefficients. The advantage is that it is easy to identify noise and speech components and hence noisy components can discard. Different estimators are developed (uses transform domain processing) for speech enhancement using Gaussian and Super-Gaussian Speech priors. Speech Presence Uncertainty is taken in to consideration for better performance in removing residual noise.

Let y(n) be the input noisy signal and b(n) be the noise and x(n) be clean speech signal. Assume noise is additive then we write y (n) = x (n) + b (n) (1)

In frequency domain processing (STFT) done on frames, due to discontinuities at frame boundaries there introduces some distortion [3]. This can be controlled by the choice of windowing function and ratio of frame increment to window length. Best choice is using Hanning window taking frame increment 2 and window length 2 for perfect reconstruction [1-3] and to attenuate discontinuities at frame boundaries. For the case of Hamming window, the ratio 4 is used. Analysis of window shift, based on pitch period works better for frequency domain processing.

• A.    Spectral Subtraction

Spectral Subtraction is one of the first and significant approaches for single channel speech enhancement [1-4]. In spectral subtraction, estimated clean speech is obtained by subtracting the estimated noise spectrum from the noisy signal (clean speech + noise) and results in estimated clean speech. Spectral subtraction suffers from remnant noise, musical noise and speech distortion [1-2].

To address this problem, several variations of the basic method are proposed. One variation is taking the control over amount of noise power subtracted from noisy power spectrum (spectral over subtraction) [3]. Here a constant subtraction factor is used for the total length of the spectrum and results in significant amount of reduction in remnant noise. For further reduction of remnant noise, another approach is that, firstly use basic spectral subtraction and obtains the enhanced speech. After that, again give the enhanced output as input and iteratively repeat the process for number of times gives better reduction in remnant noise (Iterative spectral subtraction). In real world, noise affects the speech differently for different frequencies. To deal the real world noise, rather than using constant subtraction factor for whole spectrum, the subtraction factor is set individually for each frequency band (Multi-band spectral subtraction). At low SNRs the subtraction factor is unable to adapt with variable noise characteristics [1-3]. By using masking properties of human auditory system, attenuate the noise components that are not audible due to masking (spectral subtraction using human auditory system.

Table 1. Spectral Subtraction Methodologies

• a)    Basic Spectral Subtraction

1 S( ffl ) = Y ( ^ )|2 -| В Ц

• b)    Spectral Over-subtraction

г  |Г(ю)| -^В(ю) if |Г(ю)| >(а+р)В(ю)| в| B (ю)|           else

^S ( ® )

• c)    Multi-band Spectral Subtraction

• 2 М- a ^Nf if \sH > e Y i (®t ; k. < ® < k i + -

• eYi(®)|               else

s ^{>; )}

Afterwards spectral subtraction was implemented in modulation domain. Here the subtraction is performed on the real and imaginary spectra separately, in modulation frequency domain (so it enhances the magnitude and phase).

• B.    Wavelet transform

General DFT approach is not able to localize time and frequency, i.e., it is not able to provide the exact frequency at exact time. Whereas the wavelet transform provides good time frequency analysis [10]. Hence using wavelet transform, it is able to know the frequency information at a particular time. Wavelet uses variable time windows for different frequency bands and hence better resolution is achieved at low frequency bands as well as high frequency bands. Wavelet transform is a powerful tool to deal speech signals which are normally non-stationary and hence used for noise reduction in single channel speech enhancement. After applying the wavelet transform, the coefficients can be modified by putting some threshold value such that the noise coefficients can be neglected and hence noise reduction is possible. To achieve better performance in single channel speech enhancement, where only one microphone is used, the sub-band processing approach is worthwhile. Human auditory system is divided in to 18 critical bands [10] (frequency bands) and process the signal according to these critical bands yield better results.

• C.    Stochast c Est mat on

• 1)    W ener F lter

Wiener filter suppress the noise by minimizing the Mean Square Error (MSE) between the original signal magnitude and the processed signal magnitude.

H ( ® k ) =

^Pxx ⁽ to ) P xx ⁽ ® ) + P bb ⁽ ® )

Where P ₌ ( ю ) , P_bb ( ю ) are the clean signal power spectra and noise power spectrum respectively [3, 10]. It is observed that under low SNR conditions the ratio becomes very small and approaches to zero, i.e.,

H( И ) ^ 0 and at extremely high SNR regions the ratio approaches to unity, i.e., H ( и ) ^ 1. Hence Wiener filter attenuates under low SNR and emphasizes under high SNR. Later some parameters are added to the Wiener filter to achieve different characteristics at different SNRs as

L

Where v, = -^- y. k 1 + l/

function of priori SNR and

H ( ® k ) =

(     P x ( И )    ]

( P xx ^{( И} ) + ^a P И J

Where a , в are the parameters used to obtain different attenuation characteristics for different values. It is noted that the above Wiener filter is non-causal as it requires knowledge of clean signal. Iterative Wiener filter is used for estimation in iterative fashion. Afterwards, some spectral constraints are imposed within frame and are considered for processing and constrained Wiener filtering algorithm is proposed. In sub-band Wiener filter, the signal is divided according to human auditory critical bands and Wiener estimation is applied on each band. Also while processing it is useful to vary the window size [10] according to pitch. Later perceptual constraints are introduced in Wiener filter and masking of inaudible sources is incorporated with Wiener filters.

2) Non -linear Estimators

Wiener filter assumes the DFT coefficients of both speech and noise as Gaussian random variables (STFT). Wiener filter is linear estimator as it estimates complex spectrum with MMSE. But in ML and MMSE estimators, estimation of modulus of DFT coefficients is done which is a non linear estimation process. It is noted that Wiener estimator is optimal as complex magnitude spectral estimator [3, 7, 8]. In Wiener filter, mean is calculated with X ( и ) rather than X_k . Bayesian estimators are proposed with Short-Time Fourier Transform (STFT) coefficients as well as with Short-Time Spectral Amplitude (STSA). In STSA, estimation of spectral amplitudes is done where as in STFT; estimation of complex spectrum is done.

i. Minimum Mean Square Error (MMSE) Estimator

Quality and intelligibility can improve if the estimator is optimum in spectral amplitude sense, i.e., minimizing the mean square error of short time spectral amplitude of processed and true magnitudes [7-8].

e = E

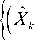
- X.)’}

Where X ^ˆ and X are the magnitudes of processed and clean speech respectively. Calculation of MMSE estimator gain [11], requires the knowledge of Bessel functions. It also requires lookup table.

v^ T r (1.5) M ( - 0.5,1; - v . )           (5)

Y .

posteriori SNR and M ( - 0.5,1; — v_k ) is hypo geometric function. However, computationally efficient techniques without usage of Bessel functions are proposed. This can be achieved by either Maximum A Posteriori or MMSE estimation of spectral power.

ii. MMSE Log-Spectral Amplitude Estimator (MMSE-LSA)

Mean square error or cost function is included with logarithm function as

e = E

log X . - log - X

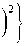
The Gain for MMSE-LSA Estimator is given as [3, 11]

V k . exp J !

Y .      2

to   - 1

e — dt ^

t v.

This estimator results in a slightly higher speech distortion but lower residual noise than MMSE STSA (due to higher suppression i.e. smaller gain). It suffers from less residual noise than MMSE Estimator [3, 7, 11] and also maintains the quality of enhanced speech same as obtained with MMSE (even by taking Speech Presence Uncertainty (SPU) in to account). Note that SPU in log STSA is unworthy. All the estimators are generalized using a cost function with different values of α, β, as [11]

C = ( х в - X в ) 2 ( х К ^аХ , 2 ^п ) (8)

Different values of α, β, results in different estimators. Gains of each estimator is used for obtaining enhanced speech using (Gain multiplied with noisy speech)

X = Gain. Noisy

One of the estimators is β-order MMSE estimator with gain given as

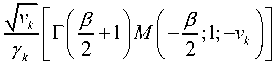
This estimator provides better trade-off between residual noise and speech distortion. Better results can achieve if appropriate stochastic parameters are used for β value adaptation like masking threshold. Decreasing β below 0 causes an increase in the noise reduction and speech distortion. β estimator with β = -1 slightly shows better performance than MMSE STSA and LSA estimators in terms of PESQ [7,11,13]. Weighted Euclidean (WE) Estimator gain can be calculated as

r^f p + 1 + Л M (_ p + 1 ,1; -)

V v_k  (   2      )   (    2        ^k )

^{Y k}  rf p + 1 ) M f- p ,1; - v_k 1

1 2 J       I 2       k )

Under high SNR conditions all the above mentioned estimators approaches to wiener estimator [11].

• iii.    Maximum A Posteriori (MAP) Estimator

In MAP approach choose

And

6 = arg max P(6 / x)

p (6 / x) = p (x /6) p(6)(13)

Here MAP Estimator does not depend on p(x) and the MAP estimator is given as [3, 14]

6 = argmax [ln( p (6 / x)) + ln( p (6)]

MAP estimators of the magnitude-squared spectrum is obtained as

5 +

। e+ (1 + 5 ) | ^£ l l a )

2(1 + 5 )

The above mentioned MAP estimator is a powerful tool to improve speech intelligibility, at extremely low SNR level [14]. In some estimators, the DFT coefficients of speech and noise are assumed as Gaussian probability density function (pdf) and also several works used nonGaussian speech priors and better results are obtained [12,14].

iv. Estimators Using Super-Gaussian Speech Priors

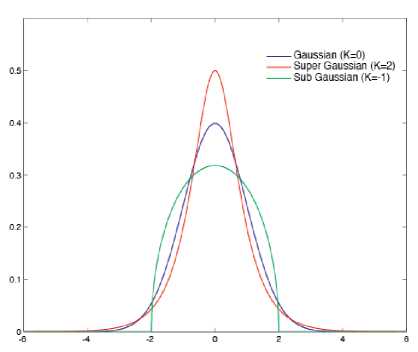
Fig.2. Super Gaussian Distribution - Lesser Variance and High Spectral Peaks

Under Gaussian speech and noise priors, Wiener estimator is regarded as optimal. But for lesser frame length durations (<25ms) rather than using Gaussian assumption for speech DFT coefficients Laplacian and Gamma (Super-Gaussian) assumption yields better results as the variance is less for super-Gaussian (Laplacian, Gamma) than Gaussian . Also using super-Gaussian ones can obtain distribution with sharp peaks and less tails than Gaussian as shown in Fig.2. Hence researchers proposed estimators using super-Gaussian speech priors.

Use of super Gaussian speech priori gives better noise reduction but with poorer noise equality, i. e, increased noise reduction and significant rise in distortion. SuperGaussian priors do not exactly match with the distributions measured and hence further improvements in noise reduction is still possible by considering better spectral variance estimators and alternate PDF models. Some researchers have shown that using Speech Presence Uncertainty along with estimator gives better performance (to deal residual noise). The Speech Uncertainty probability is given by

P ( H . >  ( ® k )) =

P ( Y K H 1 ^k ) P ( H 1 ^K )

P ( Y k | H _o ^k ) P ( H K ) + P ( Y k | h 1 ^k ) P ( H 1^K )

Where H 1 is for speech presence hypothesis and H 0 is for speech absence hypothesis. Multiply the estimator gain with SPU probability to obtain the enhanced speech.

D. Modulation Domain

Intelligibility is a key factor for understanding good percentage of words even under noisy conditions (reduces listening effort). At low SNRs normal people can understand more words than patients with hearing impaired [4]. Intelligibility can be possible if there is significant reproduction of modulation of the spectral amplitudes. The processing of the signal in modulation domain is given in Fig. 3

Noisy Speech

Modulation Spectrum

Fig.3. Processing of Noisy Speech in Modulation Domain

• IV.    NMF AND HMM A PPROACHES

Speech enhancement methods like, Wiener filter, Spectral Subtractions are not able to give satisfactory results for non-stationary signals. To achieve significant improvement in processed speech (quality) noise type must be known in advance. To deal this, enhancement methods based on HMM and NMF were used. In these methods noise and speech samples have to be trained.

• A.    Speech Enhancement Using NMF

NMF based speech enhancement is a decomposition technique useful for denoising and especially for denoising non-stationary signals like speech. In this technique, decomposition of signal is done as a combination of non-negative building blocks. Optimal choice of W and H are obtained by solving      V « WH

[15, 17]. In speech enhancement problem, it is considered that, the signal V as spectrogram and the building blocks, W as set of specific spectral shapes and H as activation levels respectively. Generally researchers use Kullback -Leibler (KL) divergence as one of the main objective function. Variants of NMF can be obtained by choosing different objective functions. Three important phases of processing the signal are 1) Training phase 2) Denoising phase 3) Reconstruction phase. In training phase, Nonnegative matrix factorization is performed on the clean speech and noise (Assume availability of spectrograms of clean speech and noise), minimizing KL divergence between V and WH and also between    and speech              speech speech                                              noise

. And the mean and variance for noise and noise noise .

speech H blocks are computed. In denoising, fix W blocks and find H, so that it minimizes the KL divergence [15]. Later, update blocks using any class of NMF algorithms and finally reconstruct the enhanced spectrogram. NMF can be implemented as supervised and unsupervised.

• B.    Supervised Speech Enhancement using NMF

Let Y, S, B be matrices of complex DFT coefficients of noisy, clean speech, noise. The Non-negative transformation for Y, S, B is obtained and those are given as V, X, u such that    vh =|yh\P, xh = ssh\p,ukt = \nh\p, where p=1 and 2 for magnitude spectrogram and power (Magnitude square) spectrogram. In supervised approach, prior to enhancement basis matrix for speech, noise has to be learnt. Let it be       and      and obtain combined speech           noise basis vector as

W = \^р^оР. ]

And noisy matrix obtained as (W is fixed)

• V, - W\ht = [Wp^WoPe ][ h,(s ’Th,( n ’ T ] "(18)

Finally enhanced speech is obtained using

XX =      W (P) h,$)       v

‘    W (P) h,(x) + W (n) h;n). ‘ as Wiener gain. The advantage with supervised approaches is that, no need of finding noise power spectral density and hence these approaches gives better results in enhancement process even for non-stationary noise [17].

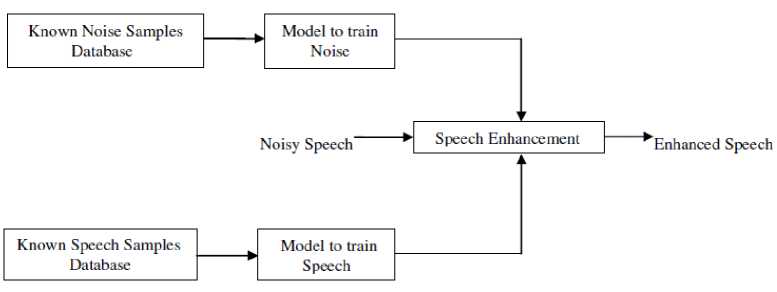
Fig.4. Block Diagram for Supervised Speech Enhancement Methods (NMF/HMM)

• C.    Unsupervised Speech Enhancement using NMF

Here the noise basis vectors are learned during intervals of speech pauses. By keeping noise basis constant during speech activity period and parameters like speech basis, NMF coefficients of speech and noise are learned [17]. This learning is done by minimizing Euclidean distance and enhanced speech is obtained using the above Wiener relation.

• D.    Different Classes of NMF

Classes of NMF algorithms are Multiplicative Update Algorithm, Gradient Descent Algorithm, and Alternating Least Squares Algorithm

• 1)    Multiplicative Update Algorithm

• 1)    Initialize W as random dense matrix

• 2)    Initialize H as random dense matrix

• 3)    Update W, H up to several iterations

H = H .*(W T A )./( W T WH + e )       (20)

W = W .*( AH T yiWHH T + e )      (21)

- 9

Where E is used to avoid zero, E = 10

• 4)    Repeat step 3 for several iterations

• 5)  End

• 2)    Gradient Descent Algorithm

• 1)    Initialize W as random dense matrix

• 2)    Initialize H as random dense matrix

• 3)    Update W,H up to several iterations

  H = H - E

  H

  
  

  d f d H

  
  
  
  

W = W - E w f             (23)

• 4)    Repeat step 3 to for several iterations

• 5)  End

• 3)    Alternating Least Squares Algorithm

• 1)    Initialize W as random Matrix

• 2)    Set all negative elements in H to zero.

• 3)    Solve for W using

HH^TW^T = HA T              (24)

• 4)    Set all negative elements in W to zero

• 5)    Repeat step 2 to step 5 for several iterations

• 6)    End

• 4)    Constrained NMF

• 1)    Initialize W as random dense matrix

• 2)    Initialize H as random dense matrix

• 3)    Update W, H up to several iterations

H = H .*(W^TA )./( W^TWH + P H + e )     (25)

W = W .*( AH T )./(WHH^T + a W + e )     (26)

• 4)    Repeat step 3 to for several iterations

• 5)    end

• E.    Hidden Markov Model (HMM) Based Method

Markov process is a stochastic model used to model a random system that changes states according to some transition rule which depends on current state (only). HMM is a model which relates hidden variables and mixture weights through Markov process [19]. Let’s see how HMM is applied to speech enhancement. First obtain the sample vectors for noisy, clean speech and noise signals. This can be done by framing each of the signals and for each frame one sample vector is obtained. Let the noisy signal be yk = sk + bk. Now noisy signal is divided into frames and are stored in vector (for each frame) as Ут =[Ук,Ук-1,....Ук-т+i] , where T denoting the frame index. In similar manner, obtain the vectors s andb . The speech signal and noise signal are first modeled using HMM and each of its output density as Gaussian Mixture Model (GMM) [18]. Here speech and noise process is Auto Regressive (AR) and the hidden state probability for speech is given as sK = {Sj,....sK }

K f (sK; 2) = 2™ZH az_J ( stVt ^)     (27)

Q i     Q k t = 1

Where a_ZgZ О P ( Z j ) is initial state probabilities, here Z indicates states and the equation

I f ( St\zt ;O) =^ w, ZTg ( St ;0, q,Zr)        (28)

i = 1

is GMM which depends on state. C_{i , z} is the covariance matrix of state z. And the combined HMM is obtained using Noise HMM and Speech HMM [19]. For finding the parameters, Expectation Maximization (EM) algorithm is used. Non-negative HMM is developed and implemented with MMSE estimator. Later, it was shown that better performance can achieve if HMM is combined with super Gaussian priors.

• F.    Phase Processing + Amplitude Processing

Human ears are insensitive to phase information. But later researchers came to know that phase is important factor for Intelligibility [3]. In [21], it is showed that signal reconstruction is possible using phase- only reconstruction. By combining processed phase with amplitude estimators, better enhanced speech may be obtained. From perceptual point of view, at high SNR noisy speech phase is close to clean speech phase and hence the noisy phase is used to replace clean phase. However, when SNR drops low, noisy phase shows a negative effect and it might be perceived as “roughness” in speech quality [3, 21], i.e., even for clean magnitude spectrum at low SNR there is inability to recover clean speech with unperceivable distortion.

At the early research time, researchers observed the magnitude spectrogram and phase spectrogram and came to a conclusion that spectral and temporal information obtained by phase spectrogram is insignificant (due to phase wrapping) when compared to the information obtained by magnitude spectrogram. Later researchers showed that by using group delay plot (derivative of phase with frequency) and instantaneous frequency plot, enough information about the speech signal can be obtained. Interestingly same information obtained by magnitude spectrogram can be obtained using derivatives of spectral and temporal phases. If phase systems are minimu m or ma ximu m, Hilbert transform is used to relate log-magnitude and phase which means either only the spectral phase or the spectral amplitude is required for signal reconstruction. But for the signals like speech, maximum/minimum phase is restricted. It is noted that the SNR obtained when noisy magnitudes mixed with phase which is less distorted results in SNR improvements up to 1 dB. The STFT magnitude spectrum is important than phase spectrum, for segment length between 5 ms to 60 ms, and for segments which are shorter than 2 ms and longer than 120 ms, the phase spectrum plays crucial role. In contrast to this, signal segments of 32 ms length [21], overlap of 7/8th (Rather than 50%) during the STFT analysis, along with zero padding, the performance of magnitude-based speech enhancement can be significantly improved if processed phase is taken into account.

The first and foremost approach is GL iterative approach (Griffin and Lim) [21]. In GL approach, updated phase information is retained where as the updated magnitudes are replaced. Later (Real Time Iterative Spectrogram Inversion) RTISI-LA is developed in which phase is updated in multiple frames. In sinusoidal model-based phase estimation, fundamental frequency is used for estimating the clean spectral phase which is taken from the degraded signal. Each of these techniques has different difficulties. Hence enhanced spectral magnitudes combine with processed phases can overcome these limitations. In [22], authors derived phase aware magnitude estimator based on MMSE estimator. One phase-aware complex estimator is the Complex estimator with Uncertain Phase ( CUP ) [23]. The initial phase estimation can be done using signal characteristics. The open issue is phase estimation is difficult at very low SNRs. This may overcome by joining the different phase processing approaches into iterative phase estimation approaches. In addition, better performance yields by considering speech spectral coefficients as Gamma distributed and noise spectral coefficients as Gaussian [23]. Clean speech phase estimation is an interesting field of research in area of speech enhancement.

• V.    C HALLENGES AND O PPORTUNITIES

Speech enhancement objective is to improve quality and intelligibility. Existing methods are not able to improve both quality and intelligibility and trade-off between the quality and intelligibility is always needed. Development of methods which provides less distortion while processing the speech is needed. Assuming speech priors as Super-Gaussian in different estimators improved the performance of estimators but still these distributions not exactly match with speech DFT coefficients. There is a need for sophisticated speech priori assumptions. Under High SNR conditions available speech enhancement methods are providing better results, but at low SNR conditions there is necessity to develop improved techniques. To deal with non-stationary signals like speech, there is need to develop supervised methods using NMF and HMM. Better results are obtained if statistical estimators are used along with NMF and HMM. Use of Super-Gaussian in NMF and HMM may also lead to new speech enhancement methodologies. Unsupervised and Supervised methods ignored phase information or phase processing due to its complexity. Joint Amplitude and Phase Estimation methods will place significant position in speech enhancement field. Amplitude estimators combine with processed phase information will open new techniques in the field of speech enhancement.

• VI.    C ONCLUSION

In this paper, different speech enhancement methodologies and its developments are discussed. Bayesian Estimators and Frequency domain approaches plays significant role in noise reduction. Using speech presence uncertainty along with estimators can improve the performance of Estimators. Supervised methods like NMF and HMM are helpful for dealing Non-stationary signals. Super-Gaussian Estimators included in NMF gives better noise reduction. There is need in considering processed phase information along with amplitude information.