A Survey on Statistical Based Single Channel Speech Enhancement Techniques

Published Online November 2014 in MECS

The main aim of speech enhancement is to improve the performance of speech communication systems in noisy environments. Speech enhancement can be applied to a speech recognition system or a mobile radio communication system, a set of low quality recordings or to improve the performance of aids for the hearing impaired. The interference source may be a wide-band noise in the form of a white or colored noise, a periodic signal such as in room reverberations, hum noise, or it can take the form of fading noise. The speech signal may be simultaneously attacked by one or more noise source. There are two principal perceptual criteria for measuring the speech enhancement system performance. The first criterion is the quality of the enhanced signal measures its clarity, distorted nature, and also the level of residual noise in that signal. The second criterion is measuring the intelligibility of the enhanced signal. This is an objective measure which provides the percentage of words that could be properly identified by listeners. Most speech enhancement systems improve the signal quality at the expense of reducing its intelligibility. Our goal in speech processing is to obtain a more convenient or more useful representation of information carried by the speech signal.

In general, to perform reliably in noisy environments, there exists a requirement for digital voice communications, automatic speech recognition systems and human-machine interfaces. For example, in hands-free operation of cellular phones in vehicles, the speech signal which is to be transmitted may be contaminated by reverberation and background noise. In several cases, these systems work well in nearly noise-free conditions, however, their performance deteriorates rapidly in noisy conditions. Therefore, the development of preprocessing algorithms for speech enhancement is always interesting. The goal of speech enhancement varies according to particular applications, such as to increase intelligibility, to boost the overall speech quality, and to improve the performance of voice communication devices. Speech analysis is used to extract features directly pertinent for different applications. Speech analysis can be implemented in time domain (operating directly on the speech waveform) and in the frequency domain (after a spectral transformation of speech) [1].

Many single-channel speech enhancement approaches have been proposed over the years. Different types of algorithms are proposed for speech enhancement such as spectral subtraction, wiener filtering, statistical based methods, noise estimation algorithms [2]. Speech signal representation in time domain measurements includes energy, average zero crossing rate and the auto correlation functions [3]. In time domain approaches, which includes Kalman filter based methods, the speech enhancement is performed directly on the time domain noisy speech signal via the application of enhancement filters (i.e. Linear convolution). In the frequency domain approaches, a short-time Fourier transform (STFT) [4] is typically applied to a time domain noisy speech signal. This class of methods includes, among others, spectral subtraction and Bayesian approaches. The enhancement can also be performed in other domains. Different algorithms are proposed to evaluate the speech enhancement that is intelligibility of processed speech and quality of processed speech [2]. For example, the so-called subspace approach is obtained by applying a Karhunen-Loeve Transform (KLT) [5] to the time domain signal, performing the enhancement in that domain and finally going back to the time domain using an inverse KLT operation. In all these approaches, the modification should be made to the noisy speech.

The paper is organized as follows: section II presents an overview of speech enhancement, classification of speech enhancement methods. Section III discusses the statistical based approaches for speech degraded by background noise. Section IV presents the challenges and opportunities in speech enhancement. Section V concludes with a summary and conclusion.

Approaches for Speech Enhancement

Additive Noise Removal

Subspace Approach

Auditory Masking Methods

Statistical Based Approaches

1. Wiener Filtering

2. ML Estimators

3. Bayesian Estimators

4. MMSE Estimators

- MMSE Magnitude Estimator

- MMSE Complex Exponential Estimator

4. Log MMSE Estimators

5. MAP Estimators

6. Perceptually Motivated Bayesian Estimators

Time Domain Approaches

1. Comb Filtering

2. LPC based Filtering

3. Adaptive Filtering

- Kalman Filtering,

- H algorithm

4. HMM Filtering

5. Neural Networks

Transform domain Approaches

1. DFT

2. DCT

3. Wavelets

4. Spectral Subtraction

Reverberation Cancellation

Temporal Processing

Cepstral Processing

1. CMS and RASTA processing

• 1.    De-Reverberation Filtering

• 2.    Envelope Filtering

Multi Speech (Speaker) Separation

I

• II.    Overview of Speech Enhancement

Enhancement means improvement in the value of quality of something. When it is applied to speech, this is nothing but the improvement in intelligibility and/or quality of degraded speech signal by using signal processing tools. Speech enhancement is a very difficult problem for two reasons. The first reason is the nature and characteristics of the noise signals can change randomly, application to application and in time. The second reason is the performance measure is defined differently for each application. There are two perceptual criteria are widely used to measure the performance of algorithms. They are quality and intelligibility.

Classification of speech enhancement methods is shown in Fig 2.1

• III.    Statistical-Model Based Methods

• A.    Wiener Filtering

Let y [n] be a discrete time noisy sequence

y (n ) = x (n) + ^n)                                         (1)

Where x[n] is the desired signal, which we also refer to as the “Object” and w[n] is the unwanted background noise. We assume x[n] and w[n] to be uncorrelated random process, wide sense stationary with power spectral density functions denoted by Sx (И) and sw (И) respectively. One approach to recovering the desired signal x [n] will rely on the additivity of power spectra

For recovering an object sequence x[n] corrupted by additive noise w[n], that is from a sequence

Y [n] = x [n] +w [n], is to find a linear filter h [n] such that the sequence x[n] = y[n]* h[n] minimizes the expected value of under the condition that the signals x[n] and w[n]

are stationary and uncorrelated and the frequency domain solution to this stochastic optimization problem is given by

H ⁽ ® ) =

^Sx ^{( и} )

^Sx ^{( и )+} s w ( И )

Which is referred as wiener filter. When the signals x[n] and w[n] meet the conditions under which the Wiener is derived, that is stationary and uncorrelated object and background, the wiener filter provides noise suppression without considerable distortion in the object estimate and the background residual. The required power spectra ^( _И )

and s^( _m ) can be estimated by averaging over multiple frames when x[n] and h[n] sample functions are provided. The background and desired signal are non-stationary in the sense that their power spectra change over time, that is they can be expressed as time varying functions ^s x ^{( n, И} ) and s w ^{( n} ’ ^И ) . Thus every frame of STFT is processed by different wiener filter. We can express time varying wiener filter as

H s ⁽ PL , ^И ) =

S x (PL, И )

Where s^, ( pL, И ) is an estimate of time varying power spectrum of x[n].

Jacob Benesty [6] proposed a quantitative performance behaviour of the wiener filter within the context of noise reduction. The author showed that within the single channel case the a posteriori signal/noise (SNR) (defined when the Wiener filter) is larger than or adequate to the a priori SNR (defined before the Wiener filter), indicating that the Wiener filter is usually ready to reach noise reduction. The amount of noise reduction is normally proportional to the amount of speech degradation. The authors showed that speech distortion will be higher managed in three alternative ways. If we have some a priori data (such as the linear prediction coefficients) of the clean speech signal, this a priori data will be exploited to attain a noise reduction while maintaining the level of speech distortion. Once no a priori data is offered, we will still reach better control of noise reduction and speech distortion by properly manipulating the Wiener filter, leading to a sub optimum wiener filter. Amehraye, D.Pastor A. Tamtaoui [7] proposed a speech enhancement technique, which deals with musical noise resulting from subtractive type algorithms and particularly Wiener filtering. The authors compared many methods that introduce perceptually motivated modifications of standard Wiener filtering and propound a new speech enhancement technique. The main aim is to improve the quality of the enhanced speech signal provided by standard Wiener filtering by controlling the latter via a second filter regarded as psychoacoustically motivated weighting factor. Philipos C. Loizou [8] introduced a new speech improvement approach of a frequency specific composite gain function for Wiener filtering, intended by the recently established finding that the acoustic cues at low frequencies will improve speech recognition in noise by the combined electrical and acoustic stimulation technique. With this modification the planned approach is in a position to recover a lot of low frequency (LF) parts and enhance the speech quality adaptative procedure is employed to see the low frequency boundary. Jacob Benesty [9] presents a theoretical analysis on the performance of the optimal noise-reduction filter within the frequency domain. By using the autoregressive (AR) model each the clean speech and noise are modelled, built relation between the AR parameters of the clean speech and wiener filter and noise signals. The authors showed that if the noise is not predictable, the Wiener filter is mostly related to the AR parameters of the desired speech signal. When the desired signal is not predictable, then the Wiener filter mostly related to the AR parameters of the noise signal. Chung-Chien Hsu [10] proposed a signal-channel speech enhancement algorithm by applying the traditional Wiener filter within the spectro-temporal modulation domain. In this work the multiresolution Spectro-temporal analysis and synthesis framework for Fourier spectrograms extends to the analysis-modification-synthesis (AMS) framework for speech enhancement. Feng Huang [11] proposed a transform-domain Wiener filtering approach for enhancing speech periodicity. The enhancement of speech is performed based on the linear prediction residual signal. Two sequential lapped frequency transforms are applied to the residual during a pitch-synchronous manner. The residual signal is effectively described by two separate sets of transform coefficients that correspond to the periodic and aperiodic elements, severally. For the transform coefficients of the periodic and aperiodic components, different filter parameters are designed. A template-driven methodology is employed to estimate the filter parameters for the periodic components, whereas in the case of aperiodic components, the filter parameters can be calculated by using local SNR for effective noise reduction.

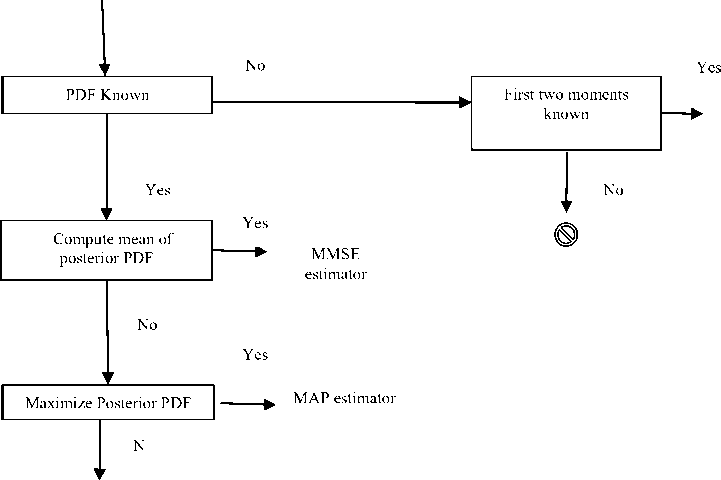
• B .    Maximum-Likelihood Estimators

The estimator based on maximum likelihood principle, termed the Maximum Likelihood Estimator (MLE). We can obtain an estimate that is about the Minimum Variance Unbiased (MVU) estimator. Variance of estimator should be minimum. Because, as the estimation accuracy improves the variance decreases. The estimator is unbiased means, on the average the estimator will yield the true value of unknown parameters. Estimation accuracy directly depends on probability density function (PDF). The attributes of approximation relies on the property that the MLE is asymptotically (for large data) efficient.

The advantage of MLE is that we can consistently find it for a given data set numerically. This is because the Maximum Likelihood Estimator (MLE) is determined as the maximum of known function, namely, likelihood function. Fig 3.1 shows the search of MLE. [12].

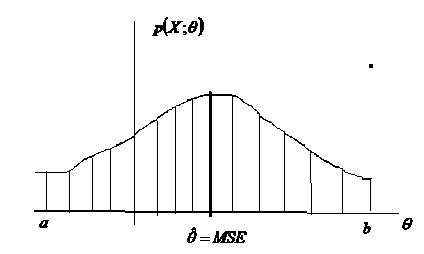
Fig. 3.1 Grid search for MLE

If, for example, the allowable value of 9 lie in the interval [a, b], then we need only maximize p ( X ; 9 ) over that particular interval. The “safest” way to do this maximization is to perform a grid search over [a, b] interval. As long as the spacing between ⁹ is small enough, then we are guaranteed to find the MLE for the given set of data.

M.L.Malpass [13] proposed enhancing speech in associate additive acoustic noise surroundings is to perform a spectral decomposition of a frame of noisy speech associated to attenuate a specific spectral prong relying on what proportion the measured speech and noise power exceeds an estimate of the background noise. By using a two-state model for the speech event that is speech absent or speech present and by using the maximum likelihood estimator of the magnitude of the acoustic spectrum results during a new category of suppression curves which allows a tradeoff of speech distortion against noise suppression. Takuya Yoshioka [14] proposed a speech enhancement methodology for signals contaminated by room reverberation and additive background noise. The subsequent conditions are assumed: (1) The spectral parts of speech and noise are statistically independent Gaussian random variables. (2) In every frequency bin the convolutive distortion channel is modeled as associate auto-regressive system. (3) The speech power spectral density is modeled as associate allpole spectrum, whereas that of power spectral density of the noise is assumed to be stationary and given prior to. Under these conditions, the proposed methodology estimates the parameters of the channel and those of the all-pole speech model supported the maximum likelihood estimation methodology.

• C.    Bayesian Estimators

In case of classical approach to statistical estimation within which the parameter 9 of interest is assumed to be a a deterministic however unknown constant. Instead of assuming ₉ is a random variable whose specific realization we tend to should estimate.

On the other hand, Classical approach, finds it tough to make use of any prior knowledge. So Bayesian approach will improve the estimation accuracy. Second, Bayesian estimation is beneficial in situations where an MVU estimator cannot be found. The Bayesian approach to data modelling is shown in Fig 3.2 [12].

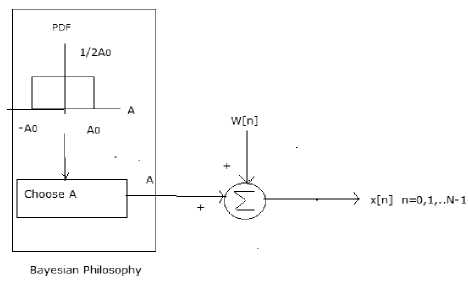
Fig. 3.2 Bayesian Approach to data modeling

In classical approach we might choose for a realization of noise w(n) and add it to given A. This procedure is continual for M times. Every time we need to add new realization of w(n) to given A. In Bayesian approach, for every realization we might opt for A according to PDF and so generate w(n) as shown in Fig 3.3. We might then repeat this procedure for M times. In the classical approach, we would obtain for every MSE for every assumed value of A and MSE depends on A. In Bayesian, Single MSE figure obtained would be average over PDF of A and MSE does not depend upon A. Ephraim [15] developed a Bayesian estimation approach for enhancing speech signals which have been degraded by statistically independent additive noise. Especially, maximum a posteriori (MAP) signal estimators and minimum mean square error (MMSE) are developed using hidden Markov models (HMM’s) for the clean signal and the noise process. The authors showed that the MMSE estimator comprises a weighted sum of conditional mean estimators for the composite states of the noisy signal (pairs of states of the models for the signal and noise), where the weights equal the posterior probabilities of the composite states given the noisy signal. A gain-adapted MAP estimator is developed by using the expectationmaximization (EM) algorithm. Chang hui you [16] proposed Beta-order minimum mean-square error (MMSE) speech enhancement approach for estimating the short time spectral amplitude (STSA) of a speech signal. Analyzes the characteristics of the Beta-order STSA MMSE estimator and therefore the relation between the worth of and therefore the spectral amplitude gain perform of the MMSE technique. The effectiveness of a variety of fixed values in estimating STSA supported the MMSE criterion is investigated. Whenever the speech level is above the noise level, a priori SNR involves a frame delay and is no longer a smoothed SNR estimate, which is more appropriate for non stationary signals. Whenever the speech level is close to or below the noise level, a priori SNR estimation equation has a smoothing effect and musical noise is greatly reduced. Therefore, total suppression is improved. Sriram Srinivasan [17] proposed a Bayesian minimum mean square error approach for the joint estimation of the short-term estimator parameters of speech and noise. By this work's author used trained codebooks of speech and noise linear predictive coefficient to model the a priori data needed by the Bayesian scheme. In distinction to current Bayesian estimation approaches that take into account the excitation variances as a part of the a priori data, within the proposed technique authors computed online for every short-time segment, based on the observation at hand. Consequently, the strategy performs well in non-stationary noise conditions. The resulting estimates of the speech spectra and the estimates of noise spectra are employed in a Wiener filter. Estimation of the functions of the short-term predictor parameters is additionally selfaddressed, especially one that results in the minimum mean square error estimate of the clean speech signal. The Bayesian approach is given in Fig 3.3. [12].

LMMSE Estimator

Fig. 3.3 Bayesian Approach

Signal processing Problem

Bayesian Approach

Classical Approach

Fig. 3.4 Classical Versus Bayesian Approach

Achintya Kundu [18] considered a general linear   density function (PDF) of the clean signal employing a model of signal degradation, by modeling he probability   Gaussian mixture model (GMM) and additive noise by a

Gaussian PDF, and also derived the minimum mean square error (MMSE) estimator which is non-linear. Takuya Yoshioka [19] proposed an adaptive noise suppression methodology for non-stationary noise based on the Bayesian estimation methodology.

The subsequent conditions are assumed:

• (1)    Speech and noise samples are statistically independent, and that they follow auto-regressive (AR) processes. (2) The noise AR model prior distribution of the parameters of a current frame is similar to the posterior distribution of these parameters calculated within the previous frame. Based on these conditions,

The proposed method approximates the AR model parameters with the joint posterior distribution and therefore the speech samples are used by the variational Bayesian method. Moreover, described an efficient implementation by assuming that each covariance matrix has the Toeplitz structure. The difference between classical approach and a Bayesian approach is shown in the Fig 3.4. [12].

Eric Plourde[20] proposed a new family of Bayesian estimators for speech enhancement wherever the cost function includes each an power law and a weighting factor. The parameters of the cost function, and thus of the corresponding estimator gain, are chosen supported characteristics of the human auditory system, it is found that selecting the parameter leads to a decrease of the estimator gain at high frequencies. As a result this frequency dependence of the gain will improve the noise reduction, whereas it limits the speech distortion. So new estimators attains higher improvement performance than existing Bayesian estimators (MMSE, STSA, LSA, WE error), each in terms of objective and subjective measures. P. J. Wolfe [21],[22] masking thresholds were introduced within the Bayesian estimator’s cost function to make it a lot of perceptually significant whereas in P.C. Loizou [23], many perceptually relevant distortion metrics were thought of as cost functions. One in every of the cost functions that was found to yield the most effective leads to [23] was based the perceptually weighted error criterion employed in speech coding. In [23] the error spectrum is weighted by a filter that is that the inverse of the original speech spectrum. This was adapted from [23] by proposing a generalization of the MMSE STSA cost function wherever the error between the estimated and actual clean speech STSA is weighted by the STSA of the clean speech raised to an exponent, the resulting estimator is termed Weighted Euclidian (WE). Another generalization of the MMSE STSA cost function was planned by You et al. [24] within the Beta-Order STSA MMSE estimator; that we are going to denote as Beta-SA for convenience. The Beta-SA estimator applies a power law to the estimated and actual clean speech STSA within the square error of the cost function. The advantage of the proposed method is both weighting and compression in the cost function. Estimators are more advantageous at low SNRs because distortions of high frequency contents of speech, such as fricatives will be less perceptual in heavy noise (low SNR), but they could become more perceptible in regions where noise is weak.

For low SNRs gain is decreased and heavy noise will mask speech signal, so estimator will apply small gain such that remove much of noise.

Eric Plourde [25] proposed a new cost function that generalizes those of existent Bayesian STSA estimators so get the corresponding closed-form answer for the best clean speech STSA. In this approach, associate degree estimate of the clean speech derived by minimizing the expectation of a cost function that penalizes errors within the clean speech estimate. Beta-Order STSA MMSE estimator applies a power law to the estimated and actual clean speech STSA within the square error of the cost function. Jincang hao [26] proposes the speech model is assumed to be a Gaussian mixture model (GMM) within the log-spectral domain. This is often in distinction to most current models in the frequency domain. Precise signal estimation could be a computationally indictable problem. The authors derived the three approximations to boost the efficiency of signal estimation. By using Kullback–Leiber (KL) divergency criterion the Gaussian approximation transforms the log-spectral domain GMM into the frequency domain exploitation. The frequency domain Laplace technique computes the maximum posteriori (MAP) estimator for the spectral amplitude. Similarly, the log-spectral domain Laplace technique computes the log-spectral amplitude of the MAP estimator. Further, the gain and noise spectrum adaptation are implemented using the expectation–maximization (EM) algorithm inside the GMM under Gaussian approximation.

P.Spencer Whitehead [27] proposed a robust Bayesian analysis is employed, so that to analyze the sensitivity of the algorithms to the errors in the case of noise estimate and improve the SNR ratio. Eric Plourde [28] proposed a Bayesian short-time spectral amplitude (STSA) estimation for single channel speech enhancement, the spectral parts assumed unrelated. However, the assumption is inexact since some correlation is present in the practice. The authors investigated a multidimensional Bayesian STSA estimator that assumes correlated spectral parts. The author derived closed-form expressions for higher and a lower bound on the specified estimator. Joint fundamental and model order estimation is a very important drawback in many applications like speech and music processing. Jesper Kjær Nielsen [29] developed an approximate estimation algorithm of those quantities using Bayesian interference. The interference regarding the fundamental frequency and therefore the model order relies on a probability model that corresponds to a minimum of priori information. From this probability model, the precise posterior distribution of the fundamental frequency is provided. Nasser Mohammadiha [30] presented a speech enhancement algorithm that relies on a Bayesian Nonnegative Matrix Factoring (NMF) each Minimum Mean square error (MMSE) and maximum a-Posteriori (MAP) estimates of the magnitude of the clean speech DFT coefficients are derived. To use the temporal continuity of the speech signal and noise signal, a proper prior distribution is introduced by widening the NMF coefficients posterior distribution at the previous time frames. To perform the above ideas, a recursive temporal update scheme is proposed to get the mean of the prior distribution, Further, the uncertainty of the priori data is ruled by the shape parameter of the distribution that is learnt automatically based on the nonstationarity of the signals.

• D.    MMSE Estimator

Y= h(X) + V, Where Y is noisy vector, h is a known function, and V a noise vector.

The posterior probability of X is given by

p ⁽ x / y ) =

p ⁽ y / x ) p ⁽ x )

J p ( y I x ) p ( x ) dx

The mean of X according to p(x/y):

^{x (} y ) = E ⁽ x / y ) = J xp ( x I y ^x

An estimator x ˆ for x is a function

x : y ^ x ( y )

The value of ^{x ( y} )

at a specific observed value y is an estimate of x. The mean square error of an estimator xˆ is given by

MSE (x ) = E (| X - ;x( y ) 2)

The minimum mean square error (MMSE) estimator x ˆ _MMSE is the one that minimizes the MSE.

xmmse (y ) = E (XIY = y)

The MMSE estimator is unbiased.

xmmse (Y ) = E(X)

The posterior MSE is defined as (for every y):

MSE (x I y ) = E (| X - ;x( y) 21Y = y)

with minimal value MMSE(y)

Yariv Ephraim [31] proposed the class of speech enhancement systems which capitalize on the major importance of the short-time spectral amplitude (STSA) of the speech signal in its perception. The author derived the MMSE STSA estimator, based on modeling noise and speech spectral components as statistically independent Gaussian random variables. Analyzed the performance of the proposed STSA estimator and compare it with Wiener estimator based STSA estimator. MMSE STSA estimator examines the quality of signals or their strengths under noisy conditions and in the regions where the presence of signal is uncertain. The MMSE STSA estimator is combined with the complex exponential of the noisy phase in constructing the enhanced signal. a priori probability distribution of the speech and noise Fourier expansion coefficients should be known to derive MMSE STSA estimator. Example, Zelinski and Noll [32], [33] gain normalized cosine transform coefficients are approximately Gaussian distributed. Porter and Boll [34]

proposed that the amplitude of a gain normalized Fourier transform coefficient are gamma-like distributed. This model leads to a Rayleigh distribution for the amplitude of every signal spectral part, and assumes insignificant probability for low amplitude realizations. Therefore, this model will cause less suppression of the noise than different amplitude distribution models (e.g., gamma) that assume high probability for low amplitude Realizations. Ephraim [35] derived a short-time spectral amplitude (STSA) estimator for speech signals that MMSE of the log spectra and examine it in enhancing noisy speech. It was found that the new estimator is effective in enhancing the noisy speech, and it considerably improves, the quality of speech. Zhong-Xuan Yuan [36] proposed a hybrid algorithm that incorporates the (MMSE algorithm and the auditory masking algorithm for speech enhancement. This hybrid algorithm yield reduction in residual noise compared with that in the enhanced speech produced by the MMSE algorithm alone. Guo-Hong Ding [37] proposed a unique speech enhancement approach, known as power spectral density minimum mean-square error    (PSD-MMSE)    estimation-based    speech enhancement, that is implemented within the power spectral domain wherever stationary random noise may be modeled as exponential distribution. Speech magnitude-squared spectra can be modelled as mixed exponential distribution and an MMSE estimator is built based on the parametric distributions. Li deng [38] proposed a unique speech feature enhancement technique based on nonlinear acoustic environment model, probabilistic model that effectively incorporates the phase relationship between the clean speech and therefore the corrupting noise within the acoustic distortion method. The core of the enhancement algorithm is that the MMSE estimator for the log Mel power spectra of clean speech supported the phase-sensitive environment model. The clean speech joint probability and noisy speech joint probability are modeled as a multivariate Gaussian. Since a noise estimate is needed by the MMSE estimator, a high quality, successive noise estimation algorithm is additionally developed and given. The sequential MAP (maximum a posteriori) learning for noise estimation is better than the sequential maximum likelihood learning, each evaluated under the identical phase-sensitive. Li Deng [39] proposed an algorithm which exploits joint prior distributions within the clean speech model that incorporate each the static and frame-differential dynamic cepstral parameters. From the given the noisy observations, full posterior probabilities for clean speech can be computed by incorporating a linearized version of a nonlinear acoustic distortion model. The ultimate kind of the derived conditional MMSE estimator is shown to be a weighted sum of three separate terms, and therefore the sum is weighted once more by the posterior for every of the mixture component within the speech model.

The first of the three terms is shown to arrive naturally from the predictive mechanism embedded within the acoustic distortion model in the absence of any prior data. The remaining two terms result from the speech model using solely the static prior and solely the dynamic proir, respectively. The main innovations of the author’s work are:

• 1)    Incorporation of the dynamic cepstral features within the Bayesian framework for effective speech feature enhancement.

• 2)    A new enhancement algorithm using the full posterior that elegantly integrates the predictive data from the nonlinear acoustic distortion model, the prior data based on the static clean speech cepstral distribution, and therefore the prior based on the frame-differential dynamic cepstral distribution;

Rainer Martin [40] proposed a minimum mean-square error estimator of the clean speech spectral magnitude that uses each parametric compression function within the estimation error criterion and a parametric prior distribution for the statistical model of the clean speech magnitude. The novel parametric estimator has several famous magnitude estimators as a special solution and, in addition, estimators that combines the beneficial properties of various known solutions. Yoshihisa Uemura [41] revealed new findings regarding the generated musical noise in minimum mean-square error short-time spectral amplitude (MMSE STSA) process. The authors proposed a objective metric of musical noise based on kurtosis change ratio on spectral subtraction (SS). Additionally found a stimulating relationship between the degree of generating musical noise, the strength parameter of Spectral Subtraction processing, the shapes of signal’s probability density function, The proposed algorithm is aimed to automatically evaluate the sound quality of various forms of noise reduction ways using kurtosis change ratio. Philipos C. Loizou [42] presents a unique speech enhancement algorithm which will considerably improve the signal-to-residual spectrum ratio by combining statistical estimators of the spectral magnitude of the speech and noise. The noise spectral magnitude estimator comes from the speech magnitude estimator, by transforming the a priori and also a posterior SNR value. By expressing the signal-to-residual spectrum ratio as a function of the estimator’s gain function, and also derived a hybrid strategy which will improve the signal-to-residual spectrum ratio when the a priori and the a posterior SNR are detected to be under 0 dB. T. Hasan Md.K. Hasan [43] proposed a new MMSE estimator for DCT domain speech enhancement assuming the two state possibilities of signal and noise DCT coefficients, and also proposed the constructive and destructive interferences. The optimum non-linear MMSE estimator may be derived by considering the conditional events. Yu Gwang Jin [44] proposed a unique speech enhancement algorithm based on data-driven residual gain estimation. The system consists of two stages. The noisy input signal is processed at the first stage by conventional speech enhancement module from that each enhanced signal and several other SNR-related parameters are obtained. At the second stage, the residual gain, which is estimated by a data driven methods, is applied to the improved signal to regulate it more. Timo Gerkmann [45] derived a minimum mean square error (MMSE) optimal estimator for clean speech spectral amplitudes, is applied in single channel speech enhancement. As opposition to state of art estimators, the optimal estimator derived for a given clean speech spectral phase. Finally, it shows that the phase contains extra data which will be exploited to distinguish the outliers within the noise from the target signal.

• E.    Log-MMSE Estimator

Jason Wung [46] proposed a unique post-filtering method applied after the log STSA filter. Since the postfilter comes from vector quantization of clean speech information, it is a similar result of imposing clean supply spectral constraints on the enhanced speech. Once combined with the log STSA filter, the extra filter will noticeably suppress residual artifacts by effectively lowering the residual noise of decision-directed estimation similarly at reducing the musical noise of ML estimation. Bengt J. Borgstrom [47] proposed a family of log-spectral amplitude (LSA) estimators for speech enhancement. Generalized Gamma distributed (GGD) priors are assumed for speech short-time spectral amplitudes (STSAs), providing mathematical flexibility in capturing the statistical behaviour of speech.

• F.    MMSE Estimation of the pth-Power Spectrum

Y=X+W

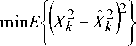
Where X and X ˆ are clean speech and estimated clean speech respectively.

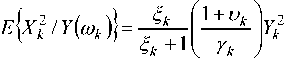
The Minimum Mean Square Estimation for the Pth order is given by minE

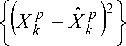
Estimated Amplitude for the P th order is given by

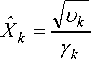
Ti p + 1 |ф| p ,1; - и

(2 И 2     k

^pY k

Gain function :

G p ( 5k , Y k )

Yariv Ephraim [48] derived an exact expression for the covariance of the log-periodogram power spectral density estimator for a zero mean Gaussian process.

G.MMSE Estimators Based on Non-Gaussian

Distributions

In case of MMSE algorithms, we assume that the real and imaginary parts of the clean Discrete Fourier

Transform (DFT) coefficients are modeled by a Gaussian distribution. However, the assumption of Gaussian, holds asymptotically for long duration analysis frames. For these specific frames the span of the correlation of the signal is much shorter than that of the DFT size. This assumption holds good for the noise DFT coefficients, but it does not hold good for the speech DFT coefficients. These coefficients are typically estimated using relatively short (20–30 ms) duration windows. This is the reason why we use non-Gaussian distributions for modeling the real parts and imaginary parts of the speech DFT coefficients. Specifically, the Gamma probability distributions or the Laplacian probability distributions can be used to model the distributions of the real parts and imaginary parts of the DFT coefficients. For example, MMSE estimator can use a Laplacian PDF for the noise DFT coefficients and gamma PDF for the speech DFT coefficients and vice versa. In summary, MMSE estimators that use non-Gaussian pdf's for speech and noise Fourier transform coefficients yields improvements in performance.

Saeed Gazor [49] proposed an algorithm that the noisy speech signal is first decorrelated and then the clean speech components are estimated from the decorrelated noisy speech samples. The distributions of clean speech signals are assumed to be Laplacian and the noise signals are assumed to be Gaussian. The clean speech components are estimated either by using maximum likelihood (ML) or by using minimum-mean-square-error (MMSE) estimators. These ML and MMSE estimators require some statistical parameters derived from speech and noise. Rainer Martin [50] proposed an algorithm that the estimating DFT coefficients within the MMSE sense, when the prior probability density function of the clean speech DFT coefficients will be modelled by a complex laplacian or by a complex bilateral Gamma density. The PDF of the noise DFT coefficients can be modelled as complex Gaussian density or complex Laplacian density. Estimators based on Gaussian noise model and the super Gaussian speech model provides a higher segSNR than linear estimators. Estimators based on Laplacian noise model achieve the better performance only for high SNR conditions but provide better residual noise. The proposed estimator requires adaptive a priori SNR smoothing and limiting to achieve high residual noise quality. Richard C Hendriks [51] proposed a technique for speech enhancement based on the DFT. The generalized DFT magnitude estimator obtained from the results has a special case, the present scheme is based on Rayleigh speech priors, whereas the complex DFT estimators generalize existing schemes are based on Gaussian speech priors, Laplacian speech priors and Gamma speech priors. Richard C. Hendriks [52] proposed a deterministic model in combination with the well-known stochastic models for speech enhancement. The authors derived a MMSE estimator under a combined stochastic–deterministic speech model with speech presence uncertainty and showed that for various distributions of the DFT coefficients the combined stochastic–deterministic speech model coefficients. Here, the clean speech DFT coefficients are characterized by deterministic, however unknown amplitude and phase values, whereas the noise DFT coefficients are assumed to follow a zero-mean Gaussian probability density function (PDF). The use of the proposed estimator leads to less suppression as compared to the case where speech DFT coefficients are assumed stochastic. Yiannis Andrianakis [53] proposed a speech enhancement algorithm that takes advantage of the time and frequency dependencies of speech signals. The above dependencies are incorporated within the statistical model using ideas from the Theory of Markov Random Fields. Above all the speech STFT amplitude samples are modelled with a Chi Markov Random Field priors, and then used for the estimator based on the Iterated Conditional Modes methods. The novel prior is additionally coupled with a ‘harmonic’ neighborhood, that allows the directly adjacent samples on the time frequency plane, also considers samples that are one pitch frequency apart, therefore on benefit of the made structure of the voiced speech time frames. Cohen [54] has shown that consecutive samples inside a frequency bin are extremely correlated, whereas the DD approach [55] for the estimation of the a priori SNR owes its success for the most part to the exploitation of the dependencies between successive spectral amplitude samples of speech. Correlations exist between consecutive samples on the frequency axis of the STFT, that stem not only from the spectral leakage caused by the tapered windows employed in the calculation of the STFT, however from the most common modulation of the amplitude of samples that belong to adjacent harmonics of the voiced speech frames, as according in [56]. In the case of linear mean-squared error (MSE) complex-DFT estimator (eg. Wiener filter), its magnitude-DFT (MDFT) counterparts are considered in the context of speech enhancement. Therefore Hendrick R.C. [57] proposed a linear MSE MDFT estimator for speech enhancement. The author presented linear MSE MDFT estimators depends on the speech DFT coefficients distributions, unlike the linear complex-DFT estimators. Bengt Jonas Borgström [58] proposed a stochastic framework for designing optimal short-time spectral amplitude (STSA) estimators for speech enhancement assuming phase equivalence of noise and speech signals. By assuming additive superposition of speech and noise, that is inexplicit by the maximum-likelihood (ML) phase estimate, effectively project the optimal spectral amplitude estimation drawback onto a 1-D subspace of the complex spectral plane, so simplifying the problem formulation. By assuming Generalized Gamma distributions (GGDs) for a priori distribution of each speech and noise STSAs, and also derived separate families of novel estimators consistent with either the maximum-likelihood (ML), the minimum mean-square error (MMSE), or the maximum a posteriori (MAP) criterion. The employment of GGDs permits optimal estimators to be determined in generalized form, so specific solutions may be obtained by substituting statistical parameters resembling expected speech and noise priors. The proposed estimators exhibit sturdy similarities to well-known STSA solutions. For instance, the Magnitude Spectral Subtracter (MSS) and Wiener filter (WF) are obtained from specific cases of GGD shape parameters. Several investigations showed that speech enhancement approaches may be improved by speech presence uncertainty (SPU) estimation. Balazs Fodor [59] proposed a new consistent solution for MMSE speech amplitude (SA) estimation under SPU, based on spread of speech priors as the generalized gamma distribution. The proposed approach shows outperform each the SPU-based MMSE-SA estimator relying on a Gaussian speech prior.

• H .    Maximum A Posteriori (MAP) Estimators

A proportional cost function results in an optimal estimator which is median of posterior PDF. For a “Hit-or-Miss” cost function the mode or maximum location of posterior PDF is the optimal estimator. The latter is termed the maximum a posterior (MAP) estimator. In the MAP estimation approach we choose 9 to maximize posterior PDF or

9 = argmax p ( 9 I x )

This is shown to minimize the Bayes risk for a “Hit-or-Miss” cost function. In finding maximum of p ( 9 / x ) we can observe that

p (91 x )= p(x91p(9)

So an equivalent maximization is of p ( _x / 9 ) p ( 9 ) . This is reminiscent of MLE except for the presence of prior PDF. Hence the MAP estimator is given by

9 = argmax p ( x 1 9 ) p ( в )

or

9 = arg max ^{[ ln (} p ⁹ / x )) + ln ⁽ p ^{( 9 ))]}

Richard C. Hendriks and Rainer Martin [60] proposed a new class of estimators for speech enhancement within the DFT domain. The authors considered a multidimensional inverse Gaussian (MNIG) distribution for the speech DFT coefficients. This distribution models a wide range of processes, from a heavy-tailed process to less heavy-tailed processes. Under the MNIG distributions complex DFT and amplitude estimators are derived. In distinction to alternative estimators, the suppression characteristics of the MNIG-based estimators can be adapted online to the underlying distribution of the speech DFT coefficients. When compared to noise suppression algorithms based on pre-selected superGaussian distributions, the MNIG-based complex DFT and amplitude estimators performance shows the better improvement in terms of segmental ratio. Though superGaussian distributions offer clearly a higher description of the speech DFT distribution than a distribution, the form of the distributions within the strategies is often chosen fixed over time and frequency. It can be advantageous to derive clean speech estimators under a distribution that may be over time and frequency. Assume Speech DFT coefficients follow MNIG distribution, motivated by the actual fact that speech could be a heavytailed method yet. Under this assumption, the speech DFT amplitudes are often shown to be Rayleigh inverse Gaussian (RIG) distributed. Under the MNIG and RIG distribution, the authors derived clean speech MAP estimators for the complex DFT coefficients and speech amplitudes, severally. Guo-Hong Ding [61] introduced maximum a posteriori (MAP) framework to sequentially estimate noise parameters. By using the first-order vector Taylor series (VTS) approximation to the nonlinear environmental function within the log-spectral domain, the estimation is implemented. Tim Fingscheidt [62] proposed a maximum a posteriori estimation jointly of spectral amplitude and phase (JMAP). It allows speech models (Gaussian, super-Gaussian. etc.) whereas the noise DFT coefficients PDF is being modelled as a Gaussian mixture (GMM). Such a GMM covers each a non-Gaussian stationary noise method, however additionally a non-stationary method that changes between Gaussian noise modes of various variance with the probability of the GMM weight.

MMSE Versus MAP

The MMSE estimator is usually tougher to derive than another estimator for random parameters like the maximum a posteriori (MAP) estimator for speech waveforms. The MMSE estimator has in observe exhibited systematically superior enhancement performance over the MAP estimator for speech waveforms. Although the MMSE estimator is outlined for the MSE distortion measure, it's optimally additionally extends over to category different distortion measures. This property doesn't hold for the MAP estimator. As a result of the perceptually significant distortion measure for speech is unknown, the wide coverage of the distortion categories by the MMSE estimator with same optimality is extremely desirable.

• I.    General Bayesian Estimators Perceptually Motivated Bayesian Estimators

Philipos [63] proposed Bayesian estimators of the short-time spectral magnitude of speech based on perceptually motivated cost functions to overcome the shortcomings of the MMSE estimator. The authors derived three classes of Bayesian estimators of the speech magnitude spectrum. The first class of estimators uses spectral peak information, the second class uses a weighted-Euclidean cost function, this function considers auditory masking effects, and the third class is designed for penalizing the spectral attenuation. From the estimation theory, the MMSE estimator minimizes the Bayes risk based on a squared-error cost function. The squared-error cost function is most commonly used because of its mathematical tractable and easy to evaluate. The disadvantage of the squared error cost function is it treated positive estimation and negative estimation errors the same way. But the perceptual effect of the positive errors (i.e., the estimated magnitude is smaller than the true magnitude) and negative errors (i.e., the estimated magnitude is larger than the true magnitude) is not the same in the applications of speech enhancement. Hence, the positive errors and negative errors need not be weighted equally. To overcome above problems proposed a Bayesian estimator of short time spectral magnitude of speech based perceptually motivated. The authors derived Bayesian estimator preserves weak segment of speech (low energy) such as fricatives and stop consonants. MMSE estimator do not typically do well with such low energy speech segments because of low segmental SNR. Estimator errors produced by MMSE estimator, WLR estimator are small near the spectral peaks and large in spectral valleys, where residual noise is audible. Bayesian estimator that emphasizes spectral valleys more than spectral peaks performed in terms of having less residual noise and better speech quality. Eric Plourde [64] proposed a family of Bayesian estimators for speech enhancement wherever the cost function includes each power law and a weighting factor. Secondly, set the parameters of the estimator based on perceptual considerations, the masking properties of the ear and also the perceived loudness of sound.

• J.    Incorporating Speech Presence/ Absence Probability in

Speech Enhancement

Nam Soo Kim [65] proposed a novel approach for speech enhancement technique based on a global soft decision. The proposed approach provides spectral gain modification, speech absence probability (SAP) computation and noise spectrum estimation using the same statistical model assumption. Israel cohen [66] proposed an estimator for the a priori SNR, and introduced an efficient estimator for the a priori speech absence probability. By a soft-decision approach, the speech presence probability (SPP) is estimated for every frequency bin and every frame. The soft decision approach exploits the robust correlation of the speech presence in neighboring frequency bins of consecutive frames. Generally, a priori speech absence probability (SAP) yields better results. Interaction between estimate for a priori SNR and estimate for a priori SAP may deteriorate the performance of the speech enhancement. The advantage of the proposed method is, for low input SNR and non stationary noise, avoids the musical residual noise and attenuation of weak speech signal components. The proposed method avoids attenuation of weak speech signal components. Rainer Martin [67] proposed a novel estimator for the probability of speech presence at every time-frequency point within the shorttime discrete Fourier domain. Whereas existing estimators perform quite dependably in stationary noise environments, they typically exhibit a large false alarm rate in non stationary noise that leads to a good deal of noise leakage when applied to a speech enhancement task. The proposed estimator eliminates this problem by temporally smoothing the cepstrum of the a posteriori signal-to-noise (SNR), and yields significantly low speech distortions and less noise leakage in each, stationary noise and non stationary noise as compared to other estimators. Zhong-Hua Fu Jhing-Fa Wang [68] addresses the problem of speech presence probability (SPP) estimation. Speech is approximately sparse in timefrequency domain, integrated the time and frequency minimum tracking results to estimate the noise power spectral density and therefore the a posteriori signal-to-noise. By applying Bayes rule, the final SPP is estimated, that controls the time variable smoothing of the noise power spectrum.

• K.    Methods for Estimating the A Priori Probability of

Speech Absence

The a priori probability of speech absence is q_k = p ( н к ) is assumed to be fixed. Q is set to 0.5 to address the worst case scenario in which speech and noise are equally likely to occur. Using conditional probabilities p ( к / H ) and p ( к / H ) a binary decision b was made for frequency bin k according to

If p ( к_к / H к ) > p ( к_к / H 0k ) ,then b_k = 0 (speech present)

Else b_k = 1 (speech absent)

The a priori probability of speech absence for frame m, denoted as qk (m) can then be obtained by smoothing the values of b over past frames qk(m)=cbk +(1 - cq(m - 1)                    (22)

Where c is a smoothing constant

Israel Cohen [69] proposed a simultaneous detection and estimation approach for speech enhancement. A detector for speech presence in the frequency domain (STFT) is combined with an estimator, this detector jointly minimizes a cost function that considers both detection and estimation errors. Cost parameters control the tradeoff between speech distortion, caused by residual musical noise resulting from false-detection and missed detection of speech components. High attenuation speech spectral coefficients due to missed detection errors may significantly degrade speech quality and intelligibility. False detecting noise transients as speech contained bins may produce annoying musical noise. Decision Directed (DD) approach may not suitable for transient environment. Since high energy noise burst may yield an instantaneous increase in a posteriori SNR and corresponding increase in a priori SNR. Spectral gain would be higher than desire value and transient noise component would be sufficiently attenuated. Rainer Martin [70] proposed an improved estimator for the speech presence probability at every time–frequency point within the short-time Fourier transform domain. In distinction to existing approaches, this estimator does not depend on adaptively estimated and so signal-dependent a priori signal-to-noise estimate. It so decouples the estimation of the speech presence probability from the estimation of the clean speech spectral coefficients in speech enhancement.

The proposed posteriori speech presence probability estimator gives probabilities near zero when the speech is absent. The proposed posteriori SPP estimator achieves the probabilities near one when the speech is present. The authors proposed a detection framework for determining the fixed a priori signal-to-noise. Smoothing posterior SNR has major advantage of reducing variance of speech presence probability estimator.

• L.    Improvements to the Decision-directed Approach

Israel Cohen [71] proposed a non causal estimator for the a priori SNR, and a corresponding non causal speech enhancement algorithm. In distinction to the decision directed estimator of Ephraim and Malah, the non causal estimator is capable of discriminating between speech onsets and noise irregularities. Onsets of speech are better preserved, whereas an additional reduction of musical noise is achieved. A priori SNR cannot respond too fast to an abrupt increase in instantaneous SNR, which yields increase in musical residual noise. A priori SNR heavily depends on strong time correlation between successive speech magnitudes. The authors proposed a recursive a priori SNR estimator. Non causal estimator incorporates future spectral measurement to better predict the spectral variance of clean speech. Israel cohen [72] proposed a statistical model for speech enhancement that takes into consideration the time-correlation between successive speech spectral parts. It retains the simplicity related to the statistical model, and allows the extension of existing algorithms for non-causal estimation. The sequence of speech spectral variances may be a random process, i.e, mostly correlate with the speech spectral magnitude sequence. For the a priori SNR, Causal and non causal estimators are derived in agreement with the model assumptions and therefore the estimation of the speech spectral parts. Cohen presented that a special case of the causal estimator degenerates to a “decision-directed” estimator with a time-varying frequency-dependent weight factor. LSA estimator is superior to STSA estimator, since it results in much lower residual noise without further affecting the speech itself. Hendriks [73] proposed noisy speech spectrum based on adaptive time segmentation. The authors demonstrated the potential of adaptive segmentation in both ML and Decision Directed methods, making a better estimate of a priori SNR. Variance of estimated noisy speech power spectrum can be reduced by using Bartlett method. But the decrease in variance causes side effects and also decreases the frequency resolution. Bartlett method was used across the segment consisting of 3 frames located symmetrically around frame to be enhanced. It decreases variance, but there is some disadvantages (i) Position of segment with respect to underlying noisy frame that needs to be enhanced is predetermined. (ii) Segments should vary with speech sounds (ideally). Vowel sounds may be considered upto 40-50ms, consonants sounds may be considered upto 5ms. Decision Directed (DD) approach with adaptive segmentation will result better approximation compared to DD approach without adaptive segmentation., No pre-echo presents with an adaptive segmentation, but. pre-echo presents without an adaptive segmentation (fixed segment),. Cyril Plapous [74] addresses a problem of single-microphone speech enhancement in noisy environments. The well-known decision-directed (DD) approach drastically limits the amount of musical noise, however the estimated a priori SNR is biased since it depends on the speech spectrum estimation within the previous frame. Therefore, the gain function matches the previous frame because of this reason there is degradation in the noise reduction performance. This causes a reverberation effect. So proposed a way known as two step noise reduction (TSNR) technique, which solves this problem, whereas maintaining the benefits of the decision-directed approach. The a priori SNR estimation is refined by a second step to avoid the bias of the Decision Directed (DD) approach, therefore removing the reverberation effect. However, for small SNRs, classic short-time noise reduction methods, as well as TSNR technique, introduces harmonic distortion in enhanced speech as a result of the unreliableness of estimators. This can be principally because of the difficult task of noise power spectrum density (PSD) estimation in single-microphone schemes. To overcome this problem, the authors proposed harmonic regeneration noise reduction (HRNR) technique.. A nonlinearity is employed to regenerate the degraded harmonics of the distorted signal in efficient way. The resulting artificial signal is made so as to refine the a priori SNR used to calculate a spectral gain able to preserve the speech harmonics. Yao Ren [75] proposed an MMSE a priori SNR estimator for speech enhancement. This estimator is also having similar benefits of the Decision Directed (DD) approach, however, there is no need of an ad-hoc weighting factor to balance the past a priori SNR and current maximum likelihood SNR estimate with smoothing across frames. Colin Breithaupt [76] proposed analysis of the performance of noise reduction algorithms in low SNR and transient conditions, where the authors considered approaches using the well-known decision-directed SNR estimator. The authors show that the smoothing properties of the decision-directed SNR estimator in low SNR conditions are often analytically described and which limits the noise reduction for wide used spectral speech estimators based on the decision-directed approach are often expected. Illustrated that achieving each good preservation of speech onsets in transient conditions on One side and also the suppression of musical noise on the opposite are often particularly problematic once the decision-directed SNR estimation is employed. Suhadi Suhadi [77] proposed a data-driven approach to a priori SNR estimation, it should be used with a large vary of speech enhancement techniques, such as, e.g., the MMSE (log) spectral amplitude estimator, the super Gaussian JMAP estimator, or the Wiener filter. The proposed SNR estimator employs two trained artificial neural networks, among these two networks, one trained artificial neural network is for speech presence, and the other trained artificial neural network is for speech absence. The classical DD a priori SNR estimator proposed by Ephraim and Malah is diminished into its two additive parts, currently represent the two input signals to the neural networks. As an alternate to the neural networks, additionally, lookup tables are investigated. The employment of those data- driven nonlinear a priori SNR estimator reduces speech distortion, notably in speech onset, whereas holding a high level of noise attenuation in speech absence. The performance of most weighting rules is dominantly determined by the a priori SNR, whereas the a posterior SNR acts simply as a correction parameter just in case of low a priori SNR. Hence, to reduce musical tones is by rising the estimates of the a priori SNR. However, as a result of the constant weighting factor close to unity, the greatly reduced variance of the a priori SNR estimate is lacking the ability to react quickly to the abrupt increase of the instantaneous SNR. Pei Chee Yong [78] proposed a modified a priori SNR estimator for speech enhancement. Well known decision-directed (DD) approach is modified by matching every gain function with the noisy speech spectrum at current frame instead of the previous one. The proposed algorithm eliminates the transient distortion speech and this algorithm also reduces the impact of the selection of the gain perform towards the extent of smoothing within the SNR estimate.

Drawbacks of fixed window:

• (i)    In signal regions which can be considered stationary for longer time than segment used, the variance of spectral estimator is unnecessarily large.

• (ii)    If the stationary of speech sound is shorter than this fixed segment size, smoothing is applied across stationary boundaries resulting in blurring of transients and rapidly varying speech components, leading to degradation of speech intelligibility.

Summary of estimators is given in table 1 (comparison between classical estimators) and table 2 (comparison between Bayesian estimators).

Difference between causal and Non-causal Estimators :

The causal a priori SNR estimator is closely associated with the decision-directed estimator of Ephraim and Malah. A special case of the causal estimator degenerates to a “decision-directed” (DD) estimator with a timevarying frequency-dependent weight factor. The weighting factor is monotonically decreasing as a function of the instantaneous SNR, resulting effectively in a very large weighting factor throughout speech absence, and a smaller weighting factor throughout speech presence.

This reduces each the musical noise and therefore the signal distortion.

Summary of estimators

Table 1. Comparison between classical estimators

Approach	Data Model/ Assumptions	Estimator	Optimality/ Error Criterion	Comments
Cramer- Rao Lower Bound (CRLB)	PDF p ( X ; 9 ) is known	If CRLB satisfies = I ( e X g ( X ) - 9 ) de This condition then the estimator is 9 = g ( x ) Where I ( 9 ) is PXP matrix depend only on 9 and g(X) is p- dimensional function of the data X.	9 achieves the CRLB, This is Minimum variance unbiased MVU estimator.	An efficient estimator may not exist. Hence this approach may fail.
Rao-Blackwell Lehmann-Scheffe (RBLS)	PDF p ( X; 9 ) is known	Find sufficient statistic T(X) by factoring PDF as p ( X ; 9 ) = g ( T ( X ) , 9 ) h ( X ) Where T(X) is a p-dimensional function of X, g is function depending on T and 9 , and h depends on X	9 is MVU estimator	“Completeness” of sufficient statistic must be checked. Dimensional sufficient statistic may not exist, so this method may fail.
Best Linear Unbiased Estimator (BLUE)	e ( x ) = н е Where H is N X p known matrix , C is the covariance matrix of X is known. Equvilently X = н е + w	9 = ( htc - 1 н — htc - 1 x	9 i for i=1.2,..p has minimum variance of all unbiased estimators that are linear in X.	If w is gaussian random vector then 9 is also MVU estimator.
Maximum Likelihood Estimator (MLE)	PDF p ( x ; 9 ) is known	9 is the value of 9 maximizing p ( X; 9 ) where X is replaced by observed data samples.	Not optimal in general. Under certain conditions on PDF (For large data), asymptotically it is MVU estimator.	If an MVU estimator exists, the Maximum Likelihood procedure will produce it
Least Squares Estimator (LSE)	x [ n ] = s [ n ; 9 ] + w [ n ] n=0,1…N-1. Where signal s [ n ; 9 ] depends on unknown parameters.	9 is the value of 9 that minimizes J ( 9 ) = ( X - S ( 9 )) T ( X - S ( 9 ))	None in general	Minimizing LS error does not translate into minimizing estimation error. If w is Gaussian random vector then LSE is equivalent to MLE.

The noncausal a priori SNR estimator employs future spectral measurements to higher predict the spectral variances of the clean speech. The comparison between the causal estimators and noncausal estimators shows that the variations are primarily noticeable throughout speech onsets. The causal a priori SNR estimator, yet because the decision-directed estimator, cannot respond too quick to abrupt increase within the instantaneous SNR, since it essentially implies a rise within the level of musical residual noise. In contrast, the noncausal estimator, have some subsequent spectral measurements at hand, is capable of discriminating between noise irregularities and speech onsets. Noncausal estimator shows the improvement within the segmental SNR and lower log- spectral distortion than the decision-directed technique and the causal estimator.

Speech enhancement gain functions are computed form (i) Estimate of noise power spectrum (ii) Estimate of noisy power spectrum. The variance of these spectral estimators degrades quality of enhanced speech. So we need to decrease the variance.

Table 2 Comparison between Bayesian estimators

Approach	Data Model/ Assumptions	Estimator	Optimality/ Error Criterion	Comments
Minimum Mean Square Error (MMSE) Estimator	PDF p ( X ; 9 ) is known, where 9 is considered to be a random variable.	9 = E ( 9 / X ) Where the expectation is with respect to posterior PDF p ( 9 / X ) = . P ( X / 9 ) P 9 ) Г p ( X / 9 ) p ( 9 ) d 9 p ( X / 9 ) is specified as data model and p ( 9 ) as prior PDF for 9 .	^ minimizes the Bayesian MSE Bmse ^, ) = E [ 9 - 1 ^ , ) 2 ] i=1,2….p Where the expectation is with respect to p ( x ; в, )	In the non-Gaussian case this will be difficult to implement .
Maximum A posterior (MAP) Estimator	PDF p ( X ; 9 ) is known, where 9 is considered to be a random variable.	9 is the value of 9 maximizes p ( 9 / X ) or the value that maximizes p ( X / 9 ) p ( 9 ) p ( X / 9 ) is specified as data model and p ( 9 ) as prior PDF.for 9 .	Maximizes the “Hit-or-Miss” function.	For PDFs whose mean and mode (location of maximum) are same, MMSE and MAP estimators will be identical.
Linear Minimum Mean Square Error (LMMSE) Estimator	The first two moments of joint PDF p ( X ; 9 ) are known	9 ) = E ( 9 ) + C^.C- i x - E ( X ))	^ minimum the Bayesian MSE of all estimators that are linear function of X.	If X, 9 are jointly Gaussian, this is identical to the MMSE and MAP estimator.

• IV.    Challenges and Opportunities

As the applications are broadened, the definition of speech enhancement is currently changing into more general. The classification of speech enhancement techniques is shown in Fig 2.1. The classification is mainly based on time domain [79], transform domain [80] [81] and statistical based approaches. It should certainly include the reinforcement of the signal from the corruption of competing speech or even from degradation of filtered version of the same signal. Signal separation and dereverberation issues are more challenging than the classical noise reduction problem. In a room and in hands-free context the signal that is picked by a microphone from a talker contains not only direct path signal, but also delayed replicas and attenuated of the source signal because of reflections from the objects and boundaries within the room. Because of this multipath propagation there will be an introduction of spectral distortion and echoes in to observation signal, termed as reverberation. This dereverberation is needed to enhance the intelligibility of the speech signal. It is crucial to determine factors that enable or prohibit humans with normal hearing to listen to and make sense of one speaker from among a multitude of speakers and/or amidst the cacophony of background noise and babble. This ability to sift and select the speech patterns of one speaker from among the numerous is labeled cocktail party effect. Thus known as a cocktail party effect. It is well known that listening during this type of situations with only one ear is annoying and it is very difficult to consider one specific signal when many of the speech signals come from all around at the same time however it will be done.

In blind source separation with multiple microphones, we tend to try and separate completely different signals coming at the same time from the various directions. The cocktail party effect might be able to separate the signal of interest from the rest that not precisely what blind source separation algorithms do.

• V.    Summary and Conclusion

In this paper overview of speech enhancement is discussed along with the classification of techniques in speech enhancement. Statistical based techniques along with their properties, limitations are explained. Comparison between classical and Bayesian estimators are explained. Disadvantage of fixed window technique is discussed in this paper. The major and vital differences between causal and non-causal estimators find a place in the discussion of single channel speech enhancement techniques. Finally, challenges and opportunities for speech enhancement are discussed in this paper.