A Weighed Least Square TDOA Location Algorithm for TDMA Multi-target

Published Online April 2011 in MECS

Available online at

The TDOA (time difference of arrival) location technique is attached to passive location domain, and is used widely owing to the high location precision. For the tri-station TDOA location system , a variety of methods are used to solve the non-linear equations, such as the Taylor expansion method, the two-step least square algorithm, the solving pseudo-linear equation, the

* Corresponding author.

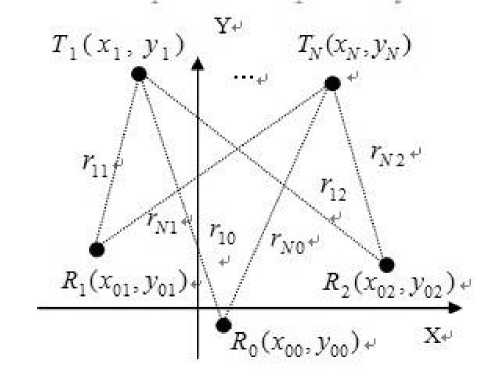
Fig.1：N-target locations in tri-sensor system modified least square algorithm, etc. [1,2,3,4]. In the multi-station TDOA location system, because of the effect of the geometry distribution of sensors, noise, and error, the ambiguity and non-solution problem appear frequently [5,6]. The areas of ambiguity and non-solution often distribute near the prolong line of the main-and sub-station.

In order to eliminate the ambiguity and non-solution problem, the measure of adding sub-station and the technology of data fusion can be used [6,7,8]. For the adding sub-station measure, the location precision within ambiguity area is improved, but the complexity of the system is increased at the same time. For the technology of data fusion, the aim of eliminating ambiguity can be achieved [9].

The time division multiple address (TDMA) system is a kind of time synchronization system, that is to say, the time of TDMA terminal is synchronous with the system. The transmitting time difference between different slots of TDMA terminals is some integer times of the slot period in its value. In reference [10], the conception of relative TDOA is used to calculate the range difference between the different TDMA terminals according to the times of arrival (TOA) of slot signal. In this paper, the time synchronization relation among multiple terminals of TDMA system is used to achieve joint TDOA location for multiple targets, the ambiguity and non-solution problems are avoided, and the location precision is improved.

Firstly, according to the TOA of slot signals among different TDMA terminals, the range difference models of multiple TDMA targets to one sensor are built. Secondly, on the basis of the traditional TDOA location algorithm, the joint TDOA ranging algorithm for multiple targets is presented to achieve TDMA multi-target location. In the end, the simulation results are presented to validate the proposed algorithm.

• 2.    TDOA location model for TDMA Multi-target

Suppose three sensors at locations R ( x , y ) , R ( x , y ) and R ( x , y ) , N targets at locations T i ( X i , y i ) ( i = 1, ™ , N) , as shown in Fig. 1.

The range from target T (x , y ) to each sensor is given as follows rij = ((xi - x о j )2 +(Ji - У о j )2 )}2,(J = 0,1,2)

Supposed the TDMA target T (x , y ) transmits a slot signal at t , the three sensors receive the slot signal at t , t andt , the relation between transmitting and receiving time is tij = ti + rj I c,(j = 0,1,2)

where c is the speed of light. For target T ( x , y ) , define the range difference between sensors j ( j =1,2) and sensor 0 as A r_y

^rij = c (ti о - tij ) = Г о - ri j,(j =1,2)

Equation (3) is the model of traditional TDOA location.

To the synchronization TDMA system, the difference of transmitting time between any two slot signals is some integer times of the slot period (T ) in its value ti - tj =AmT(4)

where A m_y is an integer.

To the first sensor, using (2) and (4), the receiving time difference between TDMA targets is ti0 -tj0 =AmT + (ri0 - rj0)1 c

Considering the coverage of the TDMA system and the guard time of signal transmission, the slot period T is generally much larger than the transmission time of slot signal among TDMA terminals. If the following relation is met:

Ts > 2|ri0 - rj0pc from (5), it gives

Amij = round((ti0 - tj0 )| Ts)

where round () is a mathematic round function. From (5), the range different between TDMA targets T ( x , y ) and T_j ( x_j , y_j ) to sensor 0 is given by

Therefore, according to the receiving time difference of slot signal between TDMA targets, the range difference to the same sensor can be acquired. The same as, the other range difference between TDMA targets to other sensors can be acquired from (3) and (8). The range difference of two targets to the sensor 0 is used in this paper.

Equation (1) is the range model, (3) is the range difference model of the same TDMA target to different sensors, and (8) is the range difference model of the different TDMA targets to the same sensor.

I.    Multi-target TDOA RANGING algorithm based on weighed least square

For the TDOA location model (3), the TDOA location algorithm for target T ( x , y ) is given as follows [2,4]

x 01 x 00    y 01 y 00 I x i

V x 02 - x 00   y 01 - y 00 JI y

( ^p1 ■^A r , r_M I V P i 2 + ^A r l2 r i 0 )

where

P y = ⁰ -5( ^r 0 j ² - ^r 002 - ^A r y ² )   ⁽ j = 1,2)

^r 0 k = ⁽ x 0 k  ⁺ y 0 k ) ^{2   (} k = 0,1,²⁾

Equation (9) is represented as

AX t= Bi

Supposed

A

- 1

^a 11

V a 21

a 12

a 22

then

X t = A ^{- 1} Bi

( m ¹ + n„ r i⁰ 1

Vmi7 + ni7 ri0 )

where my = aj 1P11 + aj 2 Pi 2

n y = a j 1 ^A r i 1 ⁺ a j 2 ^A r i 2

According to (1), it gives ri 02 = (mu + nil ri 0 - x00)2

+ ( m i 2 + n i 2 r i0 - У 00 ) 2

Simplify (14) gives airi 02 + biri 0 + ci = 0

where

22 a i = n i l ⁺ n i 2 - ¹

b i = ² n i 1⁽ m i l - x 00 ) ^{+ 2} n i 2⁽ m i 2 - У 00 )

c i = ( m i l - x 00 ) 2 ^{+ ( m}i2 - У 00 ) 2

Solving (15), the r can be acquired. The tri-station TDOA location is built by (12). This is the typical two-step least square algorithm.

The r calculated from (15) is denoted by r ˆ . For N-target of the TDMA system, there are N equations in the form of (15), and the target ranges can be get as

RR =(r10   r20   "• rN0 )T

From (8), there are N estimations of r such as itt = dRi+ it(17)

where dRi =(dril  dri2  •■•  driN )T

Ri =(r^il   r^i 2   • r^iN )T

Owing to the estimating errors inRˆ , it can be denoted by the real value r and error V as follows it. = Cr. 0 + V.(20)

where C is an N-dimension all-one column vector. V is an N-dimension column vector of estimate error.

The weighed least square estimation of r from (20) is given by [11]

Го = (C T P 1C) -1 C T Pi -1 R where P is the variance matrix of error V ,

	' Pi 11	pi 12	' pi 1 N
P i = E { VV? } =	pi 21 ■	p i 22	pi 2 N
	V piN 1	piN 2	piNN J

Define Q :

Q = P i

- 1

qi 11

qi21

;:

V q iN 1    q iN 2

qi 1N q.2 n

;

q iNN J

Thus, (21) becomes

N   N      NN

Г о = ( Z ( Г т Z q im »/< ZZ qn m ) m = 1        l = 1          / l = 1 m = 1

The estimate variance of r is given by

NN a = (CT Pf- C )-1 = (ZZ q^ )-1                                                (25)

l = 1 m = 1

Substituting (24) into (12) can realize the TDOA location. For two targets:

P =

p i 11    p i 12

V pl' 21    pi' 22 J

_a 2 =    pi 11 p i 72   pi 12 pi 71

p i 11 + pi 72 ^- p i 12 ^- pi 71

If Ри 2 = P /21 , the following variance relations are easily verified,

^ i ^ P i 11 and   ^ i ^ P i 22

Therefore, the weighed least square algorithm can improve location performance in multi-target situation.

• 3.    Multi-target TDOA location algorithm

Using weighed least square theory to estimate range, the flow of multi-target TDOA location algorithm is

• 1)    Firstly, use (15) to estimate ranges, achieve tri-station TDOA location using (12).

• 2)    Secondly, get N estimating values of range r for target T ( x , y ) using (17).

• 3)    Thirdly, acquire error variance matrix P . It can be estimated by Monte-Carlo simulation according to the range estimation process by the weighed least square algorithm and the error characteristic of tri-station location system and TDMA system. For the ambiguity or non-solution situation, a larger corresponding variance is set to make it less effective to the location precision.

• 4)    In the end, according to the weighed least square estimate algorithm, solve the ranges of every target to the first sensor, and then acquire the position information of all targets.

• 4.    Simulation analysis FOR multi-target location

  Suppose that three sensors are located at (0,0), (20000,5000) and (-20000,5000) , whose root mean square error (RMSE) of coordinate measurements and range difference is 3 meters and 30 meters respectively, while the synchronization RMSE of the TDMA system is 100 meters. 4000 times for the Monte-Carlo are used. Due to the location precision gained by weighed least square algorithm is relative to the targets’ position, the following part gives twelve groups of simulation results for two targets at different locations.

The GDOP for location precision analysis is

GDOP = ^ O x ² + O y ²                                                         (29)

where о 2 and O y ² are RMSE value in x and y coordinate respectively. The simulation results are shown in Tab.1. In Tab.1, GP1 denotes the GDOP of conventional TDOA method (CES), and GP2 denotes the GDOP of weighed least square algorithm (GLS). Fig.2 and Fig. 3 give the contrast results by two different methods for target 1 and target 2 respectively.

The conclusions from Tab.1 are given as follows.

1)In the 12 groups of target positions, for the target whose CES location performance is worse, the weighed least square algorithm can always improve its precision, and the degree of improvement is relative to the CES location performance of the other target. In group 1 and 2, where the location performance of target NO.2 is better than that of target NO.1, the location performance of target NO.1 is improved obviously by GLS. And the better improvement is get for target NO.1 in group 1 because the location performance of target NO.2 in group 1 is better than that of target NO.2 in group 2. From group 5 to 8, the CES location performance of target

NO.2 is worse than that of target NO.1. With the CES location performance become worse for target NO. 1, there is much less improvement in the GLS location performance of target NO. 2.

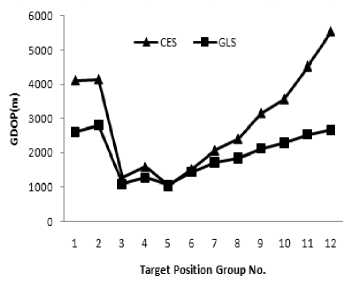
Fig.2 Location Precision Analysis for Target 1

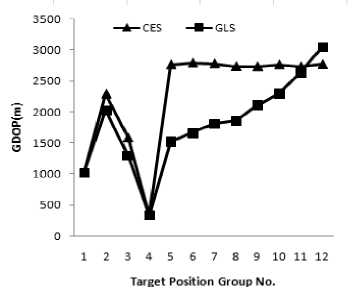
Fig.3Location Precision Analysis for Target 2

TABLE I.      L ocation precision simulation results

Position Group No.		Position(km)	GP1(m)	GP2(m)
1	Target 1	(0,200)	4131	2614
	Target 2	(0,100)	1021	1013
2	Target 1	(0,200)	4160	2808
	Target 2	(0,150)	2296	2021
3	Target 1	(50,80)	1272	1081
	Target 2	(-50,100)	1589	1291
4	Target 1	(50,100)	1594	1264
	Target 2	(-20,50)	337	334
5	Target 1	(50,50)	1033	1063
	Target 2	(80,80)	2767	1520
6	Target 1	(60,60)	1526	1439
	Target 2	(80,80)	2794	1662
	Target 1	(70,70)	2080	1724
	Target 2	(80,80)	2783	1807
	Target 1	(75,75)	2420	1846
	Target 2	(80,80)	2738	1858
	Target 1	(85,85)	3168	2119
	Target 2	(80,80)	2736	2111
	Target 1	(90,90)	3581	2294
	Target 2	(80,80)	2765	2296
	Target 1	(100,100)	4532	2537
	Target 2	(80,80)	2736	2641
	Target 1	(110,110)	5528	2674
	Target 2	(80,80)	2771	3050

• 2)    For the target whose CES location performance is better, its GLS location performance is also generally improved. From group 9 to 11, the CES location performance of target 2 is better than that of target 1. The worse the CES location performance of target NO.1 becomes, the less improvement in GLS location performance the target NO.2 gets.

• 3)    In group 5 and 12, the CES location performance is better than that of GLS slightly. This is not consistent with (28). In these situations, the CES location performance for the two targets differs a lot. This is relative to the estimation algorithm of the error variance matrix, since there are some errors in variance matrix estimating process. That is to say, the accuracy of error variance matrix plays an important role in the GLS location precision.

• 5.    Summary

In the TDOA location for multiple TDMA targets, due to the usage of time synchronization relation among multiple targets, the target location performance of weighed least square algorithm is improved compared to that of conventional TDOA method. The ambiguity and non-solution problems in the traditional TDOA location algorithm are avoided also in the proposed algorithm.