Ab initio modeling of interactions of P, H, C, S with grain boundaries in a-iron

The brittle intergranular fracture was experimentally observed in many different materials: iron and steel; nickel, copper, and high-melting alloys [1–3]. This type of brittle fracture is often accompanied by a significant reduction of fracture toughness. And, as a result, its sudden appearance can lead to a catastrophic degradation of material properties, which limits the use of many alloys. Although the mechanism of a brittle intergranular fracture depends on the material and its application, there is a distinguishing characteristic observed in all known cases. Impurities with low solubility in the volume accumulate at the grain boundaries (GB) and locally reduce the cohesive strength of a metal. These embrittling elements are called impurities because their bulk concentrations are often below the level that can be controlled during the manufacturing melting process (for example, less than 200 ppm). However, when these elements accumulate at the grain boundaries, their concentration can be very high, about 5–10 at. %.

Though researchers have been studied the influence of various impurities on the interatomic bonds on GB for several decades, some problems remain unsolved. The intergranular embrittlement, which stems from the changes in interatomic bonds on GB, is associated either with a chemical mechanism related to the features of impurity capture [4–6] or with a mechanical impact related to the atomic size of the impurity [7]. The predominant mechanism depends on a type of impurity and a material boundary. The properties of loaded interfaces (such as GB) are determined by their thermodynamic characteristics, experimental evaluation of which is not an easy process. At the same time, computer modelling from the first principles allows researchers to calculate numerically reliable thermodynamic characteristics.

In 1990 Krasko and Olsen [8] for the first time studied the behavior of various impurities (boron, carbon, phosphorus, and sulfur) on GB Σ3(111) in iron, using the ab initio modelling. Freeman and his colleagues [9–13] continued the investigation. They showed that the chemical bond between impurity elements and Fe plays an important role in the segregation processes of dissolved substances. At the same time, the modelling of the Σ5(210) boundary in the bcc iron indicated that the main factor is the size of the impurity atom [14]. Many studies on the segregation of light elements (B, C, P, N, O, and S)

at the grain boundary Σ5 in bcc iron demonstrated that different interstitial impurities may occupy different positions at the grain boundaries. However, all these atoms are embrittling elements for GB [15–17]. Several investigations [18–21] were devoted to DFT (density functional theory) modelling of the interaction of hydrogen with Σ3(111) in iron. The authors showed that hydrogen causes strong embrittlement of the considered boundary. The Σ5(310) boundary was also studied [22–24], and it was shown that internodes capture a hydrogen atom. However, only one (and not sufficiently detailed) [25] investigation was devoted to the interaction of hydrogen with the boundary Σ5 (210).

So, this work aims to study the effect of light impurities (C, P, H, S) on the grain boundaries Σ5(310), Σ5(210), and Σ3(111). We investigated the structural, electronic, and magnetic properties of these GBs, using the WIEN2k software package [26].

Methods

All calculations were carried out using the full-potential method of linearized augmented plane wave [27] with generalized gradient approximation [28], implemented in the WIEN2k software package [26]. This approach allowed us to obtain high accuracy of the simulation results within the density functional theory. For calculation, we used a powerful computing system “Tornado SUSU”. We considered three symmetric tilt GBs: Σ3(111), Σ5(310), and Σ5(210). The Σ3(111) GB is the most thoroughly studied one [18–21]. So, we used it as a model system of symmetric tilt GB with impurities in iron. The Σ5(310) boundary has the lowest formation energy in bcc iron [23]. Less studied Σ5(210) has a mutual shift of the relaxed grains, which introduces asymmetry to the system. Therefore, it is suitable as a model for an asymmetric tilt boundary in iron.

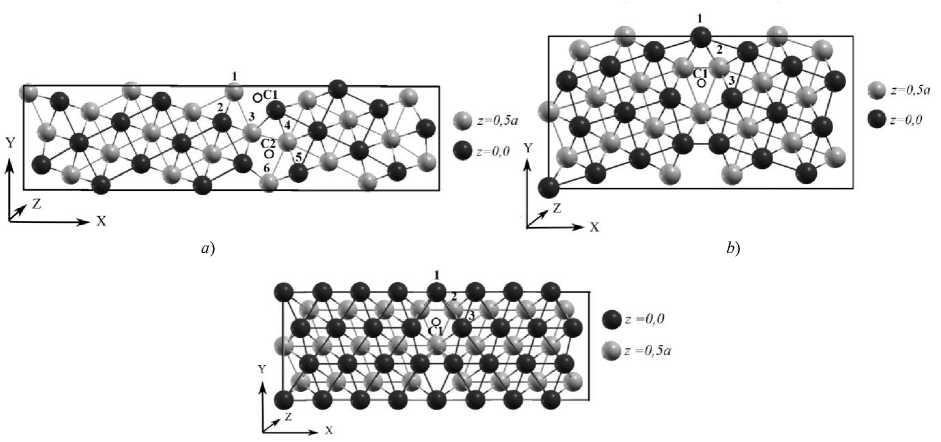
We constructed the tilt grain boundaries supercells using the coincidence site lattice (CSL) model [29]. Usually, the CSL is characterized by the Σ value, which equals the inverse density of the coincident sites. In the case of grain boundaries Σ5(210) and Σ5(310), we rotated the contacting bcc grains for each other about the common [001] axis by approximately 53,1° and 36,9°, respectively. The planes (210) and (310) were defined as the planes of grain boundaries. Similarly, we constructed the grain boundary Σ3(111). In this case, a rotation angle about the common [110] axis equaled approximately 70,53°, and the (111) plane was used as the plane of the grain boundary. The models of grain boundaries Σ5(210), Σ5(310), and Σ3(111) have elementary cells of 80, 80, and 96 atoms, respectively (Fig. 1). Note that all substitution positions 1–6 in Fig.1 lie on the grain boundary, although at a quick glance it may seem that some of them lie inside the subsurface layer.

c )

Fig. 1. Structures of a) Σ5 (210), b) Σ5 (310), and c) Σ3 (111) grain boundaries in bcc iron. Dark and light balls represent grain atoms lying in two different planes: z = 0 and z = 0,5 a , respectively ( a is the lattice constant). Positions of impurity atoms P and S: a ) 1–6; b ) 1–3; c ) 1–3. Positions of interstitial impurity atoms C and H: a ) C1 and C2; b ) C1; c ) C1

Because of periodic boundary conditions, the constructed cells represent two “grains” and two boundaries. The free surface (FS) supercell was modelled by replacing one of the halves of the cell (grain) with a vacuum of 10–12 Å length. Thus, the FS has 40 (for Σ5 (210) and Σ5 (310)) or 48 (for Σ3 (111)) atoms, separated from the neighboring cell by a vacuum of 10–12 Å in the direction of the x -axis.

For Σ5 (210) and Σ5 (310) we used 4×2×1 Monkhorst-Pack k -point mesh in the Brillouin zone [30], and for Σ3 (111) – 6×4×1. A further increase in k-points led to insignificant changes in the total energy of the systems (no more than 0,01 eV). Muffin-tin sphere radius R_mt was equal to 2,0 (iron atom, substitutional impurities P and S), 1,25 (interstitial impurity C), and 0,7 (interstitial impurity H) a.u. We chose cut-off energy of 340 eV for all systems. The supercell dimensions ( a , b , c ) for Σ5 (210), Σ5 (310), and Σ3 (111) GBs were (4 5 a , 5 a , 2 a ), (2 10 a , 10 a , 2 a ) and (4 3 a , 6 a , 2 2 a ) respectively. GB planes were perpendicular to the x- axis. Here, a is the lattice constant of bcc iron. The calculated equilibrium lattice constant of ferromagnetic bcc iron equals 2,847 Å, which is in good agreement with the experimental value of 2,86 Å [31]. Thus, the supercells had the GB areas of 36,24, 51,26, and 55,88 Ų/cell for Σ5(210), Σ5(310), and Σ3(111), respectively.

For every constructed structure with GB, we optimized the supercell lengths (both along and perpendicular to the GB) to remove stresses that had arisen in the supercell with the introduction of the GB. Subsequently, the relaxation of positions of separate atoms in the supercell was performed (the convergence criteria for Hellmann–Feynman force at each atom was 0,01 eV/Å). We simulated surfaces and hydrogen adsorption, using 40 and 48 layers of metal atoms. Metal atoms on the two lowest layers remained at their equilibrium positions. With the chosen computational parameters calculated energies have a numerical precision of 0,01 eV.

To study the intermolecular interaction and the mechanical properties of GB it is necessary to determine the following energy characteristics:

• 1)    The Griffith work, which is defined according to the thermodynamic theory by Rice and Wang [32] as a work, needed to separate a crystal along a grain boundary:

E^ = E E K- 2 Ef ,                               (1)

GW gb    fs where E gb

is the total energy of grains at their equilibrium positions for each other, and E is the total energy of relaxed free FS supercells, which form the GB. It is measured in eV. A negative value E corresponds to a decrease in the free energy of the system due to the elimination of two surfaces, i.e. this process is energetically favourable.

• 2)    The energy of GB formation in the framework of the ab initio approach

^E gb - ^E bulk

Ygb =    2S    ’ where E is the total energy of a GB supercell, which contains n Fe atoms; E is the total energy of a bulk crystal supercell, which consists of n Fe atoms and has the same volume and shape as the supercell with the GBs; and S is the area of the grain boundary interface. It is measured in J/m2.

The influence of impurity on the properties of the grain boundary can be described by the following quantitative characteristics:

• a)    The solution energy A E , defined as

A E = E X - ( n - k ) E _g b - E ( X ),                               (3)

where E _gb is the total energy of a supercell without impurity that consists of n Fe atoms; E _g ^X _b is the total energy of the same supercell with an impurity (for a substitution impurity k = 1, for an interstitial impurity k = 0); E ( X ) is the energy of one atom of the impurity (X = P, C, H, S). It is measured in eV. A negative sign of the dissolution energy indicates that an impurity is easily dissolved at a grain boundary.

• b)    Correction to the Griffith work: the cohesive energy, which is defined according to Rice and Wang model. It indicates either an enhancement (negative value) or a weakening of the intermolecular bond between Fe-atoms on the GB in the presence of an impurity [19]:

A E X w = E gb — E gb + E fs — E f X ,                          (4)

where E_fs is the total energy of the supercell of a clean free surface; E _f^X_s is the total energy of the supercell of the free surface with one impurity (X= P, C, H, S).

• c)    The binding energy of impurity to a grain boundary:

  bin     X              X

  E gb Х = ( E bulk - E bulk ) - ( E gb

  
  

  E gb ) ,

  
  
  
  

where E _bulk is the energy of the commensurate supercell of bulk Fe, E _b ^X _ulk is the total energy of the supercell with one impurity in an equilibrium position. The negative (positive) value of this energy indicates the presence of attraction (repulsion) between the GB and the impurity.

Results and discussion

In our previous works [33] we determined the formation energy of Σ3(111), Σ5(210), and Σ5(310) grain boundaries by formulas (1) and (2). It equals –4,19 eV and 1,46 J/m² for Σ3(111); –5,24 eV and 1,83 J/m² for Σ5(210); –5,77 eV and 1,44 J/m² for Σ5(310). These results are in good agreement with the results of other authors, obtained within the framework of density functional theory (Σ5(310) – 1,48 J/m² [34], 1,378 J/m² [35]; Σ5(210) – 2 J/m² [36]; Σ3(111) – 1,52 J/m² [37], 1,57 J/m² [36]). However, the experimental values / ь are about 1,5-2 times smaller than our results (0,77 J/m² and 0,985 J/m² [38,

39]) probably because in experiment it is possible to determine only an average value of / ^ over all GBs in a sample.

We chose the interstitial position for a carbon atom because this position is energetically favourable [13, 16]. Experimental studies show that at low temperatures substitution positions are energetically favourable for phosphorus. The situation changes with heating: interstitial sites become more favourable with the temperature rise [40]. Since we modelled GB at 0 K, we studied the substitution positions of a phosphorus atom in more detail. Similarly, we investigated a sulfur impurity on grain boundaries.

a)

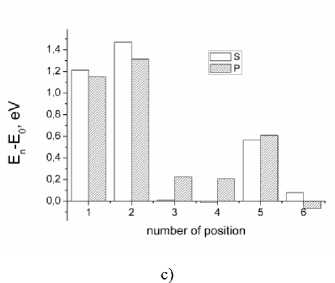
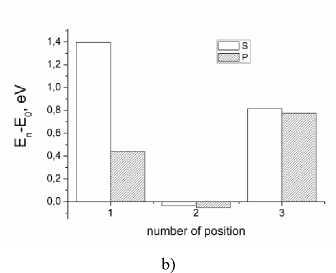
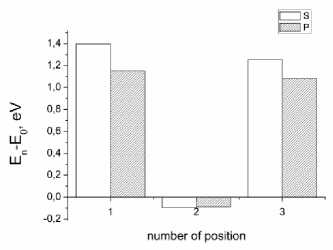
Fig. 2. Graph of the dependence of the relative energy (E n -E 0 ) of the grain boundary on the impurity position number: a ) Σ5(310); b ) Σ3(111); c ) Σ5(210)

For positions of substitutional impurities, we chose atoms with numbers 1–6 for Σ5(210) (Fig. 1, a ) and 1–3 for Σ5(310) and Σ3(111) (Fig. 1, b , c ). These atoms were replaced one by one. For interstitial positions of C and H atoms, we chose the sites C1 and C2 for Σ5(210) (Fig. 1, a ) and C1 for Σ5(310) and Σ3(111) (Fig. 1, b , c ). We calculated the total energy of the structure independence on the position of every impurity. Subsequently, we determined the ground state energy ( E ₀) as the lowest energy of a structure with each impurity (Fig. 2).

Fig. 2 shows that the systems with Σ5(310) and Σ3(111) have the lowest energy when substitutional impurities (both S and P) are located at position 2. In the case of asymmetric grain boundary Σ5(210), sulfur and phosphorus occupy sites 4 and 6, respectively. The position of carbon and hydrogen, which corresponds to the systems with the lowest energy, is C1.

Table 1 indicates that there are fluctuations of both the magnetic moment on the impurity atoms and the volume of the Voronoi polyhedron, constructed for this impurity. And there is no specific dependence for Σ5(210). For example, for the C atom in 2 different positions, the magnetic moment and the volume are the same, though the energies differ substantially (~0,6 eV). The possible explanation is that the energy components are influenced by the properties of the surrounding matrix, i. e. the asymmetry of the structure.

Table 1

The values of the magnetic moment and the volume of the Voronoi polyhedron, corresponding to the impurity atom X in different positions on the grain boundaries (X = C, H, P, S).

Type	№	Voronoi polyhedron volume of impurity, Å3				Magnetic moment Х, µ B
		S	P	C	H	S	P	C	H
Σ5(210)	1	11,99	12,05	7,57	7,11	0,01	–0,08	–0,06	–0,01
	2	10,87	10,88	7,57	6,79	–0,03	–0,09	–0,06	–0,01
	3	11,75	11,62	—	—	–0,03	–0,10	—	—
	4	11,76	11,55	—	—	–0,03	–0,10	—	—
	5	10,60	10,45	–	–	–0,05	–0,09	–	–
	6	11,14	10,92	–	–	0,02	–0,08	–	–
Σ5(310)	1	12,06	11,97	7,52	7,22	0,04	–0,07	–0,10	–0,01
	2	10,74	10,70	–	–	–0,04	–0,10	–	–
	3	11,78	11,06	–	–	–0,02	–0,08	–	–
Σ3(111)	1	12,74	12,45	7,63	6,72	0,02	–0,06	–0,10	–0,01
	2	10,47	10,45	–	–	–0,04	–0,08	–	–
	3	11,17	11,40	–	–	–0,03	–0,07	–	–

For symmetric boundaries Σ5(310) and Σ3(111) the magnetic moment of the impurities P, S, and H directly depend on the volume of the Voronoi polyhedron: the magnetic moment on the impurity atom increases with the volume increase. With the increase of the plane number, relative to the grain boundary plane, the volume and, consequently, the magnetic moment peak, then, after the decrease, the values slowly grow. Similar behaviour is observed for chromium on Σ3(111) [36]. The changes in interplanar spacings introduced by hydrogen are small enough, in comparison with P and S, which is due to the small ionic radius of hydrogen. When the carbon is located on the GB, the nearest iron atoms move away from each other, at the same time Fe-C-Fe bonds form. Magnetic moments on phosphorus (–0,09 μ B for Σ5(210); –0,07 μ B for Σ3(111)), sulfur (–0,03 μ B Σ5(210); –0,02 μ B for Σ3(111)) and carbon atoms (–0,06 μ_B for Σ5(210); –0,10 μ_B for Σ3(111)) are in good agreement with the values presented in another theoretical work (P: –0,07, –0,09 μ B ; S: –0,03, –0,04 μ B ; C: –0,12, –0,14 μ B at grain boundaries Σ3(111) and Σ5(210), respectively) [16]. For all impurities, a low value of the magnetic moment, oriented antiparallel to the surrounding iron matrix, is observed.

Table 2 presents the energy characteristics of the interaction of impurities with grain boundaries, calculated using formulas (3)–(5).

The negative value of the solution energy indicates that the impurity readily dissolves at the grain boundary. The solution energy of carbon at the GB Σ5(310) is –0,47 eV, which is in good agreement with the experimental data for this grain boundary (–0,45 eV [41]). And this value agrees with other theoretical data (–0,29 eV [42], –0,23 eV [43]). The values of the hydrogen solution energy are –0,48, –0,10, and –0,10 eV for Σ5(210), Σ5(310), and Σ3(111), respectively. These energies agree with the other theoretical results [21, 22, 24].

Phosphorus and hydrogen have positive cohesion energy at practically all positions on the grain boundaries. So, P and H are embrittling elements for these boundaries. In contrast, carbon in all cases strengthens the interatomic bonds between Fe-atoms on GB, which agrees with other data [16, 35]. In the case of the asymmetric grain boundary Σ5(210) all considered positions of sulfur have the negative cohesive energy, so S, like C, strengthens the Fe interatomic bonds on the GB. Such effect originates from the asymmetry of the surrounding matrix, which leads to the formation of Fe-S bonds. As a consequence, the bonds between the iron atoms belonging to different grains are enhanced. In the case of the boundaries Σ3(111) and Σ5(310) sulfur is an embrittling element stronger than phosphorus. This result agrees well with experimental [44, 45] and theoretical data [14, 16, 17, 37].

Table 2

Energy characteristics of the interaction of impurities with GBs: the solution energy ( Δ E ), the cohesion energy ( Δ E^X ), and the binding energy ( E _g ^bi _b ⁿ _Х )

Type

№

The solution energy, eV

The cohesion energy, eV

The binding energy, eV

S

P

C

H

S

P

C

H

S

P

C

H

Σ5(210)

1

0,02

–0,95

–0,32

–0,48

–0,27

1,67

–1,38

0,07

0,82

0,79

–1,58

–0,81

2

0,28

–0,79

0,28

–0,23

–0,02

1,83

–0,79

0,32

1,08

0,95

–0,99

–0,57

3

–1,18

–1,88

–

–

–1,48

0,75

–

–

–0,38

–0,14

–

–

4

–1,21

–1,89

–

–

–1,50

0,73

–

–

–0,40

–0,16

–

–

5

–0,63

–1,49

–

–

–0,92

1,13

–

–

0,17

0,24

–

–

6

–1,11

–2,17

–

–

–1,41

0,45

–

–

–0,31

–0,43

–

–

Σ5(310)

1

0,44

–0,70

–0,32

–0,10

1,24

0,81

–0,07

0,68

1,20

1,00

–1,27

–0,43

2

–1,05

–1,94

–

–

–0,25

–0,43

–

–

–0,29

–0,24

–

–

3

0,30

–0,77

–

–

1,10

0,74

–

–

1,06

0,93

–

–

Σ3(111)

1

–0,69

–1,61

–0,03

–0,10

2,92

0,51

–0,29

0,41

0,02

0,01

–0,82

–0,49

2

–1,27

–2,76

–

–

1,49

–0,65

–

–

–1,42

–1,14

–

–

3

–2,12

–1,93

–

–

2,34

0,18

–

–

–0,57

–0,31

–

–

The negative binding energy indicates that an impurity atom is trapped. The greater the value of binding energy, the higher the activation barrier for impurity migration in the matrix. The higher activation barrier corresponds to the lower rate at which the impurity can accumulate at the tops of the cracks, causing a fracture. The maximum value of the binding energy is observed when a carbon atom is in C1 position at the asymmetric boundary Σ5(210). In the case of hydrogen, the position with the highest value of binding energy is the same. The results are in good agreement with the data available in the literature (for carbon at Σ5(310) GB: –1,77 eV [46] and –1,51 eV [43]; at Σ5(210) GB: –1,62 eV [46], at Σ3(111) GB: –0,8 eV [16]. For hydrogen at Σ5(310) GB: –0,4 eV [22]; at Σ3(111) GB: –0,49 eV [20]; the experimental value of binding energy is –0,51 eV [47]).

Calculated binding energies of phosphorus (–0,43, –0,24, and –1,14 eV for Σ5(210), Σ5(310), and Σ3(111), respectively) also agree with the results presented in other papers (the experimental value is -0,44 eV [48]; at Σ5(310) GB binding energy is –0,4 eV [49]; at Σ5(210) GB: –1,0 eV [16] and – 0,275 eV [50]; at Σ3 (111): –1,16 eV [50, 51]). For the sulfur impurity the maximum binding energies are –0,40, –0,29 and –1,42 eV for Σ5(210), Σ5(310), and Σ3(111), respectively. These values are in good agreement with the experimental data (–0,77 eV [45]), taking into account the fact that in the experiment the binding energy was averaged over all different orientations of grain boundaries, encountered in the iron.

To summarize, the binding energy of an impurity atom is affected not only by the volume and magnetic properties of the surrounding matrix but also by the asymmetry of the structure.