Ab initio моделирование энергетических характеристик выделений карбида ванадия в ОЦК-железе

Карбиды ванадия считаются одним из важных видов твердых компонентов и измельчителей зерна в мартенситных сталях. Ванадий достаточно легко растворяется в железе и образует с ним непрерывный ряд твердых растворов, поскольку атомный радиус ванадия лишь на 6 % больше, чем у железа [1]. При этом ванадий относится к элементам, которые выклинивают γ -фазу в системе Fe-C, поэтому железованадиевые стали при содержании более 1,5 масс. % V являются ферритными. Легирование феррита ванадием повышает предел его прочности, что связано с выделением карбидов ванадия, среди которых наиболее часто обнаруживается карбид VC, имеющий кубическую решетку типа NaCl. Стехиометрический карбид VC , полученный химическим путем, имеет параметр решетки а = 0,4190 нм, а параметр решетки карбида ванадия в сталях несколько ниже – а = 0,415–0,416 нм [1]. Выделения считаются ключевыми элементами, влияющими на прочность и внутреннюю структуру стали. В процессе γ → α превращения карбиды ванадия зарождаются на границах раздела фаз и внутри зерен феррита в виде непрерывных выделений. Межфазная граница формируется между кристаллами Fe(100) и VC(100) в так называемом ориентационном соотношении Бейкера–Наттинга, которое часто наблюдается экспериментально для выделений карбидов с кристаллической структурой B1 (NaCl), внедренных в ферритовую ОЦК-матрицу [1]. Это ориентационное соотношение выражается как (001)Fe/(001)VC и [100]Fe || [110]VC.

Несмотря на важность явления для физического металловедения, расчётов энергетических характеристик поверхности раздела феррит-VC в системе Fe–V–-C практически не проводилось. Можно указать только на работу [2], где было проведено моделирование захвата атомов водорода границей раздела между карбидом ванадия и ферритом. В связи с этим представляется важным провести первопринципный расчет всех необходимых энергетических параметров нанораз-мерных выделений карбида ванадия VC в ОЦК-железе, чему и посвящена настоящая статья. Все расчеты проводились в рамках теории функционала плотности PAW-методом с учетом обобщенного градиентного приближения [3] в программном пакете VASP [4] методом суперячейки с периодическими граничными условиями.

Моделирование взаимодействия атомов ванадия и углерода в неупорядоченном твердом растворе Fe–V–C

При моделировании была использована суперячейка, состоящая из 54 узлов ОЦК-решетки. Такой выбор определялся результатами работы [5], в которой проводился анализ сходимости результатов моделирования от размера суперячейки и было показано, что ячейка из 54 узлов ОЦК-железа обеспечивает необходимую точность до 20·10^–3 эВ. Для системы Fe–V–C 53 узла заполнены атомами железа, 1 узел – атомом ванадия в позиции замещения и 1 атом углерода – в позиции внедрения. При интегрировании в обратном пространстве и вычислении электронной плотности использовалась схема Монхорста–Пака с сеткой 4×4×4 k -точек зоны Бриллюэна. Энергия

Физика

обрезания плоской волны установлена равной 420 эВ. При оптимизации атомной структуры использовался критерий сходимости: изменение энергии между двумя циклами самосогласования составляет менее 10–6 эВ, а силы, действующие на каждый из атомов, не превышают 0,01 эВ/Å. Энергия растворения примеси внедрения (С) и замещения (V) вычислялась по формуле

E d 1 = E (Fe n X) - nE (Fe) - E (X),                           (1)

где E (Fe _n X) – полная энергия системы содержащей n атомов железа (для примеси внедрения n = 54, для замещения – n = 53) и один атом примеси; E (Fe) и E (X) – энергии одного атома железа и одного атома примеси соответственно. Для расчетов, содержащих углерод в качестве эталонного состояния для C, использовалась структура графита. Параметры структуры графита были взяты из экспериментальной работы [6] ( a = b = 2,462 Å, c = 6,656 Å, α = 90°, β = 90°, γ = 120°), поскольку известно, что DFT-GGA не дает точного описания связи Ван-дер-Ваальса между слоями графита [7]. Атомы углерода в ОЦК-железе занимают преимущественно октаэдрические поры [8], поэтому при добавлении примеси углерода равновесный параметр решетки ОЦК-железа увеличивается на 0,56 %, и таким образом на один атом железа приходится объем 11,55 ų, что хорошо согласуется с данными других работ (11,42ų [9]; 11,59 ų [10]). Кроме того, решетка приобретает небольшую тетрагональность c / a = 1,01, что согласуется с другими данными ( c / a = 1,019 [11]). Было получено, что энергия растворения углерода в октапоре составляет E d1 = 0,69 эВ, что согласуется как с экспериментом 0,63–0,98 [11], так и с другими работами (0,72 эВ [9], 0,74 эВ [12]). Магнитный момент, приходящийся на атом железа, был равен 2,23 μ_В (увеличивается на 0,03 μ В по сравнению с магнитным моментом, приходящимся на один атом железа ОЦК-решетки без примеси), а для атома углерода –0,14 μ_В (знак минус означает, что магнитный момент атома углерода антипараллелен магнитному моменту атомов железа).

В данной работе производилось вычисление энергии связи ванадия с примесью углерода С, которая рассчитывалась по следующей формуле:

E h* = [ E (Fe₅ 3 VC) - E (Fe₅₄ C)] - [ E (Fe₅ 3 V) - E (Fe₅₄)],, где E (Fe₅₃V) – полная энергия системы, состоящей из 53 атомов железа и атома ванадия; E (Fe₅₄) – полная энергия системы, состоящей из n атомов железа; E (Fe 53 VС) – полная энергия системы, состоящей из 53 атомов железа, одного атома углерода и атома ванадия; E (Fe 54 С) – полная энергия системы, состоящей из 54 атомов железа, одного атома углерода С. Это выражение можно трактовать как разницу энергии растворения ванадия в чистом металле и энергии растворения ванадия в системе с примесью. Отрицательное (положительное) значение энергии связи углерода с примесью ванадия означает наличие притяжения (отталкивания) между ними.

Для оценки влияния друг на друга пары примесей (X и Y) энергия растворения каждой из них по отдельности определялась по следующей формуле:

E d ₂( F ) = E (Fe₅ 4 - m XY) - E (Fe₅ 4 - _k X) + kE (Fe) - E ( Y ),                   (2)

где m = 1 и k = 0 для примеси углерода, m = 2 и k = 1 для примеси ванадия.

При исследовании взаимодействия ванадия с углеродом в ОЦК-решетке железа были рассмотрены первые три окружения для ванадия, когда атом углерода постепенно удаляется от атома V, последовательно занимая позиции 1–3 (рис. 1). Для каждого случая размещения пары V–С выполнялась структурная и объемная оптимизации системы. При этом было обнаружено, что параметр решетки оставался постоянным и равным 2,851 Å.

В табл. 1 представлены магнитные моменты на примесях ванадия (М(V)) и углерода (М(C)), энергии их растворения, а также энергия связи между атомами С–V.

Таблица 1

Значения энергии растворения углерода в присутствии примеси замещения V, энергия растворения примеси V, энергии связи С–V

№	M(C), µ B	M(V), µ B	E d2 ( C ), эВ	E d2 ( V ), эВ	E bin ( V – C ), эВ
1	–0,08	–0,75	1,19	–0,22	0,50
2	–0,11	–1,16	0,77	–0,63	0,09
3	–0,14	–1,27	0,67	–0,73	0,01

На рис. 2 представлено сравнение результатов моделирования данной работы с имеющимися в литературе данными [13, 14].

Мирзоев А.А.,

Верховых А.В.

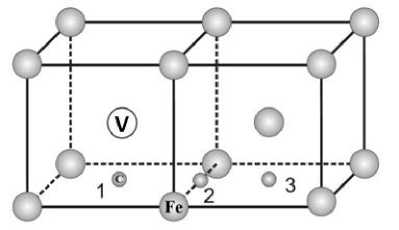
Рис. 1. Схематическое представление конфигурации V–С в ОЦК-железе. Атом углерода занимает октаэдрические позиции 1–3, которые соответствуют первым трем координационным сферам относительно ванадия

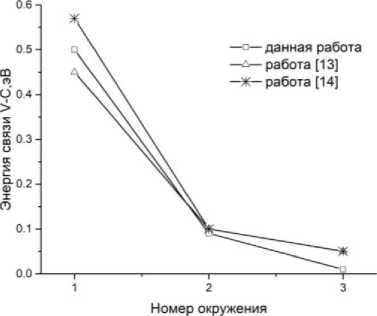
Рис. 2. Сравнение результатов ab initio расчета энергии связи V–C в ОЦК-Fe с данными Бакаева [13] и Лю [14]

Из данных, представленных в табл. 1, видно, что при сближении атомов углерода и ванадия энергия их связи существенно увеличивается. При этом она имеет положительный знак, что говорит об их сильном отталкивании при нахождении в ближайшем окружении друг друга. Это разительно отличается от случая аустенитной фазы, где термодинамические расчеты приводят к выводу о довольно сильном притяжении между C и V в ближайшем окружении [1, 15]. Вероятнее всего, природа этого отталкивания связана с магнитными эффектами. Действительно, магнитные моменты на атомах C и V также резко уменьшаются при их сближении, оставаясь антипарал-лельными моменту матрицы железа. Необходимо отметить, что в 3-м окружении относительно углерода магнитные моменты и на С, и на V практически совпадают со значениями моментов одиночных примесей углерода и ванадия в ОЦК-железе. Таким образом, основное состояние одиночной примеси соответствует наличию у нее определённого магнитного момента. При их сближении магнитные моменты значительно снижаются, что приводит к возрастанию их общей энергии, т. е. к возникновению положительной энергии связи. Тогда становятся понятными изменения знака взаимодействия С–V в аустените, где магнитные эффекты отсутствуют. Таким образом, наши расчеты показывают, что в ОЦК-фазе железа примесь ванадия активно выдавливает углерод из своего ближайшего окружения. Этот результат указывает, что образование карбида ванадия внутри бездефектной фазы ОЦК-Fe невозможно. Следствием этого обстоятельства является повышение энергии растворения ванадия и углерода в ближайших окружениях друг друга. Таким образом, ванадий уменьшает растворимость углерода в железе. Результаты энергии связи, согласно рис. 2, хорошо согласуются с данными других исследований [13, 14].

Моделирование энергии межфазной границы ОЦК-железа и карбида ванадия

Исследуемая межфазная граница формируется между кристаллами Fe(100) и VC(100) в так называемом ориентационном соотношении Бейкера–Наттинга, которое часто наблюдается экспериментально для выделений карбидов с кристаллической структурой B1 (NaCl) [16], внедренных в ферритовую ОЦК-матрицу. Это ориентационное соотношение выражается как

(001)Fe/(001)VC и [100]Fe||[110]VC.

В данном ориентировочном соотношении различные параметры решеток двух фаз создают небольшие несоответствия, которые при выделениях размером более 10 нм компенсируются дислокациями. Более того, экспериментальные наблюдения позволяют предположить, что для микровыделений возможен преимущественно когерентный интерфейс [17, 18]. По этим причинам будем рассматривать только когерентные границы.

Важно отметить, что существуют три возможных вида границы, отличающиеся сдвигом кристаллов Fe и VC вдоль границы: конфигурация, в которой атомы Fe расположены прямо над атомами C; конфигурация, в которой атомы Fe расположены прямо над атомами V; и переходная конфигурация, в которой атомы Fe имеют в качестве ближайших соседей два атома C и два атома V (рис. 3). Верхняя и нижняя панели представляют плоскости интерфейса (001)Fe и (001)VC соответственно. Наиболее стабильной является конфигурация, в которой атомы Fe расположены прямо над атомами C [2].

Физика

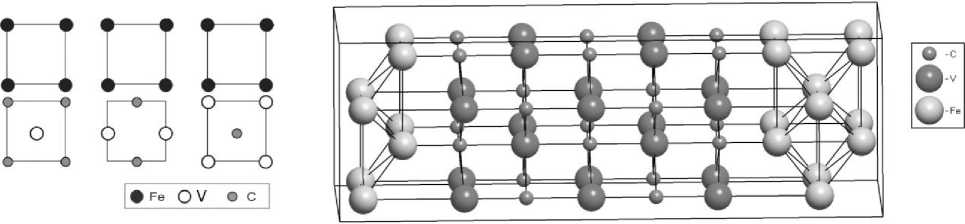
Рис. 3. Схематическое расположения атомов на межфазной границы Fe–VC

Рис. 4. Схематическое изображение структуры Fe–VC

По этой причине нами была исследована именно данная конфигурация, представленная на рис. 4. Данная структура содержит пять слоев феррита и пять слоев карбида ванадия.

Для того чтобы определить энергетические характеристики выделений карбида ванадия в железе Fe–VC, были найдены равновесные параметры решеток элементарных фаз. Полученные результаты приведены в табл. 2.

Таблица 2

Сравнение полученных нами значений равновесных параметров решетки ( a ) и модуля упругости (B) для эталонных структур ОЦК-железа, ОЦК-ванадия, углерода (графит), карбида ванадия VC в сравнении с результатами других авторов

Структура	а , Å	B, ГПа
VC	4,158, 4,160 [16], 4,155 [2]	303, 311[16]
V	2,998, 2,996 [2]	178
C	2,462, 6,656; 2,468, 8,704 [2]	–
Fe	2,831, 2,835 [16], 2,836 [2]	174,8, 175 [16]

Из табл. 2 видно, что наши результаты находятся в хорошем согласии с другими работами. После этого была рассчитана энтальпия образования карбида ванадия как разность энергий между полной энергией объемного VC и суммой энергий составляющих его элементов:

H f (VC) = E VC - mE V - ^mE C , 2m

где EVC – полная энергия VC из m атомов ванадия и m атомов углерода, а EV и EC – полные энергии на атом объемных кристаллов V и C соответственно. Было получено, что это значение равно –0,437 эВ или –42,13 кДж/моль, что находится в согласии с другими результатами [2, 19], а также с экспериментальным значением энтальпии образования карбида ванадия, близким к –50 кДж/моль [20]. Отрицательное значение указывает на то, что образование объемного VC энергетически более выгодно по сравнению с чистыми элементами. Отметим, что при нулевом давлении и температуре полная энергия и энтальпия эквивалентны.

Затем структура представленной на рис. 4 суперячейки, содержащей межфазную границу феррит – карбид ванадия, была предварительно оптимизирована для получения минимально возможной полной энергии. При этом были получены значения параметров суперячейки а = 5,82853, b = 17,44302, c = 5,88740 Å.

Энергия формирования межфазной границы Fe–VC определялась соотношением

_ E Fe/VC   E Fe   E VC

rFe'NC =         25        ’ где EFe/VC – полная энергия системы содержащей межфазную границу; EFe – полная энергия объемного кристалла феррита; EVC – полная энергия объемного кристалла VC; S – площадь границы. Было получено, что энергия формирования межфазной границы феррит-карбид ванадия равна –0,083 Дж/м2, что находится в хорошем согласии с другими результатами [2, 16]. Отрицательное значение указывает, что образование границы энергетически более выгодно по сравнению с объемными состояниями карбида ванадия и феррита. Соответственно, из этого следует, что образующиеся межатомные связи на границе сильнее, чем в соответствующих объемных фазах. Сле-

Мирзоев А.А.,                           Ab initio моделирование энергетических характеристик

Верховых А.В.выделений карбида ванадия в ОЦК-железе дует отметить, что ещё Гиббс указывал на необходимость положительного знака поверхностной энергии границы раздела жидкость–жидкость и жидкость–твердое тело для её устойчивости. Обычно предполагается, что отрицательное значение поверхностной энергии приводит к неограниченному увеличению площади границы. Но в последнее время появились примеры существования отрицательной поверхностной энергии, приводящие к образованию метастабильных или даже стабильных дисперсных структур [20]. Вполне возможно, что отрицательный знак поверхностной энергии является причиной давно отмеченной практиками исключительной мелкозернистости выделений карбида ванадия на границах ферритной фазы [1]. Однако полученное нами значение поверхностной энергии невелико по модулю. Поэтому с ростом микровыделений когерентный интерфейс из-за несоответствия параметров решеток феррита и карбида переходит в полукогерентный, что приводит к появлению дополнительного положительного вклада упругой энергии. Начиная с некоторого размера выделений VC отрицательный знак поверхностной энергии изменится на положительный и рост размера выделений остановится.

Выводы

Основные выводы статьи сводятся к следующему. Установлено, что в ферритной ОЦК-фазе примесь ванадия активно выдавливает углерод из своего ближайшего окружения. Причина такого отталкивания имеет магнитную природу. Это обстоятельство показывает, что образование карбида ванадия внутри бездефектной ферритной фазы невозможно. Поэтому наблюдаемые выделения VC внутри феррита обязательно связаны с дефектами структуры решетки. Расчетное значение энергии образования карбида ванадия –42,1 кДж/моль близко к CALPHAD-значению –50 кДж/моль, что свидетельствует о достаточной достоверности термодинамического описания карбида ванадия в рамках данного пакета. Полученная при моделировании небольшая величина энергии формирования межфазной границы феррит–карбид ванадия (–0,083 Дж/м2) позволяет объяснить хорошо известную мелкозернистость выделений карбида ванадия.

Исследование выполнено за счет гранта Российского научного фонда № 23-22-10039.