Ab-initio моделирование влияния ближнего окружения примесей углерода на энергию их растворения в ГЦК-железе

Сплавы на основе железа, несмотря на развитие производства пластмасс, керамики, композитов, остаются основными конструкционными материалами. Исключительным достоинством чёрных металлов является, прежде всего, их дешевизна, а также универсальность — при помощи небольших добавок можно резко изменить свойства их сплавов. Например, внедрение всего лишь 1 ат. % углерода радикально повышает прочность железа. Железо является полиморфным металлом [1, 2]: при нагревании выше 911 °С низкотемпературное α-железо с ОЦК решеткой превращается в γ-железо с ГЦК решеткой. Углерод растворяется в обеих фазах железа, так что при температурах выше 723–911 °С существует аустенит – раствор углерода в γ-Fe, ниже этого интервала возникает феррит –раствор углерода в α-Fe [2]. Растворимость углерода в γ-Fe довольно высока – до 2 масс. %. Напротив, α-железо растворяет очень мало углерода. Наибольшая растворимость (0,025 масс. % ) наблюдается при 723 °С. В ходе медленного охлаждения аустенита он превращается в феррит, а избыток углерода сверх равновесной концентрации выделяется в виде карбида Fe 3 C. Поэтому превращение аустенита при охлаждении стали, помимо перестройки решетки, требует прохождения процесса диффузии углерода в аустените и феррите.

Углерод образует твердый раствор внедрения как с γ-, так и с α-железом, что было установлено довольно давно [1]. По результатам совместного измерения плотности р и параметра кристаллической решетки а для серии сплавов удается рассчитать число атомов n, приходящихся на одну элементарную ячейку:

n = P a 3 Na IA ,                                        ⁽¹⁾

где A - средняя атомная масса, а N_a - число Авогадро. Наблюдавшееся возрастание n при увеличении содержания углерода в аустените и феррите однозначно свидетельствовало об образовании углеродом растворов внедрения в решетках железа. В структуре γ- и α-железа существуют пустоты (поры), ограниченные атомами железа, расположенными в вершинах октаэдра или тетраэдра, в связи с чем их называют октаэдрическими и тетраэдрическими порами. Вопрос о том, в порах какого типа расположены атомы углерода в решетках γ-Fe и α-Fe, вызвавший многолетнюю дискуссию, был решен на основе данных экспериментов по ядерному гамма-резонансу и нейтронографии [2]. Было показано, что атомы углерода в обеих решетках располагаются в октаэдрических порах (ОП).

Ридный Я.М., Мирзоев A.A., Ab-initio моделирование влияния ближнего окружения Мирзаев Д.А. примесей углерода на энергию их растворения в ГЦК-железе

В условиях быстрого охлаждения аустенита, когда диффузия углерода подавлена, происходит бездиффузионное мартенситное превращение, при котором все атомы углерода принудительно переходят в решетку мартенсита, а последняя, хотя и похожа на решетку α-железа, имеет слабую тетрагональность [1–3]. Возникновение тетрагональности и бездиффузионный характер мартенситного ГЦК-ОЦК превращения был объяснен Бейном, который обратил внимание, что ГЦК-решетку можно превратить в объемно-центрированный куб при небольшом сжатии вдоль оси ОZ и растяжении в направлениях осей OX и OY (бейновская деформация). Октапоры ГЦК-решетки вместе с располагающимися в них атомами углерода переходят только в октапоры типа «Z» решетки ОЦК-железа. При этом все атомы углерода растягивают решетку в одном Z-направлении, и она из кубической превращается в тетрагональную. Хотя теория Бейна общепри-знана, вопрос теоретического обоснования ее справедливости остается открытым.

В связи с этим, вопрос о распределении атомов углерода в ГЦК-решетке железа и их упорядочении остаётся очень важным. Очевидно, что мартенсит наследует расположение атомов углерода в аустените, которое, в свою очередь, зависит от характера взаимодействия соседних атомов углерода. Среди многочисленных характеристик аустенита наиболее чувствительной к особенностям распределения атомов углерода по октапорам оказалась активность углерода в γ-фазе α^γ _c [4]. Еще Вагнер с сотрудниками [5] показали, что при отсутствии взаимодействия между атомами углерода величина активности дается выражением:

α^γ =   ^xc   ,

c   1 - βxc где xc - доля атомов углерода в сплаве, а коэффициент р = 2. Однако результаты экспериментального изучения активности углерода в γ-железе показали, что величина αγc с увеличением содержания углерода возрастает сильнее, чем это предписывает формула (2). Было высказано предположение, что это обстоятельство связано с наличием отталкивания между ближайшими атомами углерода, что и приводит к уменьшению числа возможных мест их расположения. Даркен и Смит [6] математически оформили данную идею, введя величину е - энергию взаимодействия рассматриваемого атома углерода с другими атомами С, расположенными в любой из 12 октапор ближайшего окружения. Окончательный результат для активности оказался таким:

xc

αγ =             , c   1-(14-12θ)xc

где θ = exp( - ε kT ) . Сопоставление с экспериментальными данными для активности углерода позволило определить величину е = 0,065 эВ/атом, что для 1200 К дает р = 7,6. Видно, что учет отталкивания действительно увеличивает активность углерода в растворе.

Темкиным и Шварцманом [7], а затем Кауфманом [8] была развита модель блокировки, вко-торой выдвинуто предположение, что каждый атом С блокирует, т.е. делает недоступным для заполнения другими атомами углерода, некоторое число m октапор, ближайших к нему. В этом варианте:

ln α^γ _c = ln

x_c 1 - ( m + 1) x_c

.

Параметру m придавали значение 5 в [9], и 4 в [7]. Последнее значение можно интерпретировать в модели, что атомы углерода занимают только октапоры, расположенные в центре кубов. Квазихимическая модель (модель мягкого отталкивания) была разработана В.А. Кожеуровым [10], и позднее Мак-Лелланом [9]. В ней принимается, что атом углерода отталкивает с энергией е 1 любой атом углерода, расположенный в первой координационной сфере исходного атома. Совпадение теории и экспериментальных данных достигается при е 1 = 0,085 эВ/атом [11]. Позднее Большовым Л.А. [12] была развита более общая теория, учитывающая энергии взаимодействия пар атомов углерода не только в первой, но и последующих координационных сферах.

Поскольку все рассмотренные и сильно различающиеся модели позволяют довольно точно описать активность углерода в аустените, можно заключить, что данные об активности не позволяют провести детальную реконструкцию распределения углерода в ГЦК-железе.

Важные данные о распределении углерода получены в экспериментах по ядерному гамма-резонансу (^ГР). ^ГР-спектр аустенита имеет особенности, заключающиеся в существовании

Физика

центрального максимума от атомов железа, не имеющих в своем окружении атомов углерода, и дублета от атомов железа, соседствующих с углеродом в ближайших междоузлиях. Обзор мессбауэровских исследований распределения углерода в аустените был сделанГаврилюкомВ.Г. [13] и Надутовым В.М. [14]. Было показано, что, хотя в выводах исследователей имеются противоречия, в основном большинство авторов склоняются в пользу модели жесткого отталкивания, т.е. блокировки октапор не только в первой, но и во второй координационной сфере. Этот вывод согласуется с результатами расчета энергии взаимодействия пары атомов углерода при их расположении в первом и втором соседствах – +0,15 эВ и 0,4 эВ, полученными Гаврилюком В.Г. методом функций Грина [13]. В диссертации Надутова В.М. [14] методом Монте-Карло были получены области возможных значений энергий взаимодействия атомов углерода в первой и второй координационных сферах на основании мессбауровских экспериментов. Было показано, что энергия отталкивания атомов углерода во второй координационной сфере в разы превышает отталкивание в первой сфере и превосходит величину 0,08 эВ.

Таким образом, экспериментальными методами довольно легко определить концентрацию углерода, но достоверно установить позиции атомов углерода в решетке железа, а также структуру их ближнего порядка на данный момент времени представляет очень сложную и дорогостоящую задачу. Поэтому в последние годы все большее внимание уделяется методам перво-принципного компьютерного моделирования, главным достоинством которых является отсутствие каких-либо входных данных, влияющих на достоверность результатов при использовании минимального количества подгоночных параметров.

Джианг и др. исследовали энергию растворения углерода в ферромагнитном(ФМ) состоянии ГЦК железа в программном пакете VASP [15]. Энергия растворения вычислялась относительно графита и составила –0,17 эВ. Этот результат оказался существенно ниже экспериментального значения 0,36 эВ, полученного в работе [16] методом рассеяния электронов. В работе [17] в программном пакете SIESTA проводилось моделирование растворения углерода в АФМД состоянии ГЦК-железа, энергия составила 0,55 эВ. В ряде работ [18–20] рассматривали растворение второго атома углерода в ГЦК-решетке железа и показали, что атомы углерода предпочитают располагаться на максимально возможном расстоянии. Наиболее полный анализ растворения углерода проведён в работе Медведевой [18], но она ограничилась только немагнитным (НМ) состоянием железа.

Видно, что несмотря на значительное количество работ, посвященных изучению растворения углерода в железе, вопросы о расположении атомов углерода, энергиях их растворения, а также энергиях взаимодействия между атомами углерода остаются открытыми. В связи со всем вышесказанным, целью данной работы являлось ab-initio моделирование влияния расположения соседних примесей на энергию растворения атома углерода в различных магнитных фазах ГЦК-железа с помощью программного пакета WIEN2k [21].

Реальное ГЦК-железо существует в парамагнитном состоянии, при температурах порядка 1000 °С. Его магнитный момент равняется 0,6 μb [22]. Моделирование парамагнитного состояния методами зонной теории в пакете WIEN2k довольно затруднительно, поскольку они позволяют проводить моделирование лишь коллинеарных магнитных состояний. Поэтому мы будем описывать парамагнитное состояние с помощью двух приближений – немагнитного (НМ), в котором магнитные моменты равны нулю, и в антиферромагнитном двухслойном состоянии (АФМД). Согласно работе [23] оно является наиболее стабильным из коллинеарных магнитных состояний в ГЦК-железе.

Методы

В данной работе расчёты проводись первопринципным полнопотенциальным методом LAPW, с учетом обобщенного градиентного приближения PBE-GGA в программном пакете WIEN2k, обеспечивающим высокую точность расчета полной энергии при минимальном количестве подгоночных параметров.

В методе LAPW [24] волновые функции, зарядовая плотность и потенциал разлагаются по сферическим гармоникам в неперекрывающихся атомных сферах радиуса Rmt и по плоским волнам в остальной области элементарной ячейки. Предполагается, что внутри маффин-тин сферы зарядовая плотность сферически-симметрична. Волновые функции в междоузлии раскладываются по плоским волнам с максимальным волновым вектором Kmax. Эта величина является одним

Ридный Я.М., Мирзоев A.A., Ab-initio моделирование влияния ближнего окружения Мирзаев Д.А. примесей углерода на энергию их растворения в ГЦК-железе из основных параметров, влияющих на точность, так как она определяет число базисных функций (размер матриц). Для интегрирования в обратном пространстве и вычисления электронной плотности использовалась схема Монхорста–Пака с сеткой из N k точек в зоне Бриллюэна. ^ем больше используется точек, тем выше точность интегрирования, однако при этом возрастает расчетное время, поэтому оптимальное значение определяется из условия достижения требуемой точности энергии системы.

В нашей работе использована ГЦК-суперячейка, состоящая из 32 атомов. Была проведена оптимизация параметров моделирования, которая показала, что для достижения требуемой точности расчета полной энергии в 1 мРб/систему, необходимо использование следующих параметров: R mt (Fe) = 2,0 а.е., Kmax = 5 а.е.^–1. Эти значения совпадают с параметрами, определёнными в работах [25, 26] для ОЦК железа. Для определения геометрических параметров необходимо использование N k = 64 точки, а чтобы гарантировать точность вычисления полной энергии в 1 мРб, необходимо его увеличить до N_k =343.

Для определения энергии растворения углерода относительно фазы графита использовалась формула:

N H = E (Fe 32 C) - E (Fe 32 ) - E (C), (5) где E (Fe₃₂C₁) – энергия отрелаксированной суперячейки, состоящей из 32 атомов железа и одного атома углерода, находящегося в октапоре, E (Fe 32 ) – энергия суперячейки состоящей из 32 атомов железа, а E (C) – энергия одного атома углерода в решётке графита. Для нахождения энергии растворения второго атома углерода формула (1) преобразуется:

A H 2 = E (Fe 32 C₂) - E (Fe 32 C) - E (C). (6)

В формуле (6) E (Fe 32 C 2 ) – энергия релаксированной суперячейки, состоящей из 32 атомов железа и двух атомов углерода находящихся в октапорах.

Для нахождения энергии взаимодействия между атомами углерода из энергии системы с двумя атомами углерода вычитается энергия двух суперячеек, содержащих одиночные атомы углерода, и суммируется с энергией беспримесной суперячейки ГЦК железа:

A V = E (Fe 32 C 2 ) - 2 E (Fe₃₂C) + E (Fe₃₂). (7)

Для нахождения энергии углерода в графите мы использовали значения параметров решётки, полученные из рентгеноструктурных данных ( а = 2,462 Å, c = 6,656 Å [15]). В расчете использовались оптимизированные параметры Kmax = 5 а.е.^–1, Rmt(С) = 1,2 а.е. Количество k -точек было увеличено по сравнению с работой [15] для обеспечения точности в 1мРб/систему от N k = 256 до N k = 300.

Растворение углерода и деформация решётки

Для получения равновесных параметров суперячейки ГЦК-железа с растворенными атомами углерода была проведена атомно-силовая релаксация системы и объемная минимизация энергии. Была получена зависимость параметра решётки от концентрации углерода, приведенная на рис. 1.

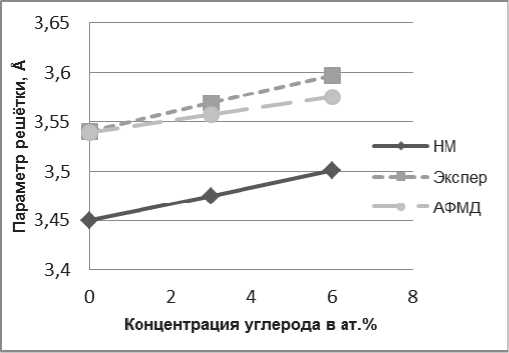
Рис. 1. График зависимости параметра решётки от концентрации углеро^а. Штрихова^ лини^ – АФМ^ состо^ние, короткий пунктир – экспериментальные значени^, сплошна^ лини^ – НМ состо^ние

При ее построении мы использовали результаты моделирования с растворенными одним и двумя атомами углерода. Было получено, что растворение одиночного атома С в НМ ГЦК-железе увеличивает параметр решётки с 3,45 Å до 3,475 Å и расталкивает ближайшие атомы железа на 7,5 %. При растворении углерода в АФМД состоянии происходит увеличение параметра решётки с 3,54 Å до

3,555 Å, и образование в первом окружении слегка несимметричного октаэдра, у которого апи-

кальный атом с противоположным направлением спина относительно других атомов железа

Физика

смещается лишь на 4 %, другой апикальный атом - на 6,5 %, тогда как планарные атомы - на 7,1 %. Полученные результаты находятся в согласии с аналогичными результатами, полученными Н. Медведевой в работах [18, 23], где при растворении углерода в НМ состоянии было получено, что атом С увеличивает параметр решётки с 3,456 А до 3,472 А и расталкивает ближайшие атомы железа на 7,7 %, а при растворении углерода в АФМД состоянии с 3,53 А до 3,55 А.

Реальное ГЦК-железо существует при температурах выше 911 °С. При такой температуре атомы углерода имеют практически одинаковую вероятность нахождения во всех конфигурационных сферах. Поэтому для вычисления параметра решётки было взято среднее значение параметра решётки, которое составило для НМ < a > = 3,5 А и для АФМД < a > = 3,575 А. Экспериментальная зависимость параметра решётки от концентрации и температуры была получена в работе [27] нейтронной дифракцией.

Проведя сравнение наших результатов с экстраполяцией экспериментальных результатов (рис. 1), мы пришли к выводу, что АФМД-состояние намного лучше описывает железо, чем НМ, и для него наблюдается довольно хорошее согласие углового коэффициента зависимости параметра решётки от концентрации углерода.

Энергии растворения атомов углерода в ГЦК железе

При использовании формулы (1), нами была вычислена энергия растворения атома углерода. В табл. 1 приведено сравнение нашей энергии с данными других работ, среди которых и экспериментальные данные для парамагнитного железа [28, 29].

Таблица 1

Значени^ энергии растворени^ о^ного атома углеро^а в октапоре ^л^ немагнитного состо^ни^ (Результаты пре^ставлены ^л^ концентрации 3 ат. % углеро^а)

Статья	Состояние	Энергия, мэВ
[28]	эксп. (парамагнитное)	360
[29]	эксп. (парамагнитное)	420
[28]	НМ	145
Данная работа	НМ	180
[17]	АФМД	550
Данная работа	АФМД	340

Видно, что энергия, полученная при растворении углерода в решётке ГЦК-железа, находя- щегося в АФМД-состоянии, практически совпадает с экспериментальным значением.

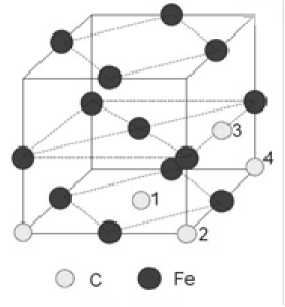
Рис. 2. Возмо^ные располо^ени^ атомов углеро^а в ^чейке Fe32

Наиболее полный анализ растворения второго атома углерода проведён в работе [18], однако он был проведен только для НМ-состояния матрицы. В суперячейке из 32 атомов железа существует 4 координационных сферы (рис. 2). Конфигурация с двумя ближайшими атомами углерода, образующими 180° C-Fe-C позицию, является наименее энергетически выгодной. Наши данные для НМ-состояния хорошо согласуются с данными Медведевой [18].

В табл. 2 приведено сравнение значений энергии растворения 2 атомов углерода, полученных в нашем расчете как для НМ, так и для АФМД-фазы ГЦК-железа. Для их получения использовалась формула (6).

Таблица 2

Значени^ энергии растворени^ второго атома углеро^а

Номер конфигурации	НМ, мэВ	АФМД, мэВ
1	260	510
2	1400	840
3	150	470
4	310	250

Проведя анализ полученных результатов, был сделан вывод, что энергия растворения второго атома углерода близка к энергии растворения первого для всех конфигураций, кроме второй.

Ридный Я.М., Мирзоев A.A., Мирзаев Д.А.

Для оценки упругих взаимодействий в рассматриваемой системе мы нашли разность полной энергии релаксированной системы и энергии системы, в которой не производилось релаксации. Назовем эту величину энергией упругой релаксации. Данные представлены в табл. 3.

Для атомов углерода, находящихся во второй координационной сфере, релаксация оказалась наиболее слабой, потому что атомы углерода находятся на одной линии и разделены одним атомом Fe, который по этой причине не двигается. Скорее всего, это обстоятельство и объясняет энергетическую невыгодность данной конфигурации.

Таблица 3

Значения энергий упругой релаксации ( E relax - E nerelax )

Номер конфигурации	НМ, мэВ	АФМД, мэВ
1	–4220	–2600
2	–3180	–2140
3	–4000	–2460
4	–3860	–2600

Для вычисления энергии взаимодействия между атомами была использована формула (7). В табл. 4 мы привели значения энергий растворения второго атома углерода для различных конфигураций в суперячейки состоящей из 32 атомов железа.

Таблица 4

Значения энергий взаимодействия между атомами углерода

Номер конфигурации	Гаврилюк В.Г. [13], мэВ	Данная работа, НМ, мэВ	Данная работа, АФМД, мэВ
1	150	80	170
2	400	1220	500
3	–	–30	130
4	–	130	–90

Видно, что учет магнитных эффектов (АФМД-состояние матрицы) несколько уменьшает отталкивание атомов углерода во второй координационной сфере, но увеличивает его в первой и третьей сферах. Атомы углерода в ГЦК-железе отталкиваются и предпочитают занимать наиболее удалённые позиции. Полученные нами значения энергии взаимодействия между атомами углерода в АФМД-состоянии матрицы хорошо согласуются с работой Гаврилюка В.Г. [13], в которой он получил указанные энергии, используя метод функции Грина. Это говорит о том, что АФМД-приближение для описания магнитного состояния может быть использовано для расчета как структуры реального ГЦК-железа, так и энергии взаимодействия атомов углерода в нем.

Заключение

Таким образом, в результате проведенных исследований:

• 1.    Были найдены: энергия растворения приходящаяся на один атом углерода (при концентрации 3 ат.%) и энергии растворения второго атома углерода (при концентрации 6 ат.%, в зависимости от их взаимного расположения) в суперячейке из 32 атомов ГЦК решётки железа.

• 2.    Растворение одиночного атома С в НМ ГЦК-железе увеличивает параметр решётки с 3,45 Å до 3,475 Å и расталкивает ближайшие атомы железа на 7,5 %. При растворении углерода в АФМД-состоянии происходит увеличение параметра решётки с 3,54 Å до 3,555 Å и образование в первом окружении слегка несимметричного октаэдра.

• 3.    Показано, что между соседними атомами углерода в ГЦК-железе наблюдается отталкивание при их расположении в первой, второй и третьей координационных сферах. При этом наиболее сильно отталкивание между вторыми ближайшими соседями.

• 4.    Показано, что для моделирования свойств ГЦК-железа с примесями углерода лучше использовать АФМД-состояние матрицы, чем НМ-состояние.