Ab initio modelling of a bilayer graphene

Bilayer graphene (BLG) is an intermediate structure between graphene and graphite consisting of only two graphene sheets. It has three configurations: a metastable AA structure obtained experimentally [1–3], a stable and well-studied AB structure (Bernal configuration [4]), and twisted bilayer graphene (tBLG), where two graphene layers are rotated by a small relative angle [5]. The latter structure has promising properties and may be of interest for nanoelectronics [6, 7], though it is difficult to obtain experimentally, and its model is too demanding for computer simulation. The intermediate A(B) structure (between AA and AB configurations), which has a bandgap of about 0,35 eV [3], also has possible applications in electronics and nanoelectronics, for example, as a channel for a field-effect transistor [1–3]. To investigate the BLG electronic properties, using the density functional theory, we needed the geometrical models. Therefore, in this research, we obtained the models of different BLG configurations and studied their structural properties and the interlayer binding energies.

Models and simulation details

For calculations, we utilized the SIESTA software package with an atomic-like basis set [8] and the VASP code with a plane wave basis set [9]. In both packages, the periodic boundary conditions were implemented. For exchange-correlation potential, we used local electron density approximation, LDA (Ceperley-Alder functional, CA [10]), and generalized gradients approximation, GGA (Perdew-Burke-Ernzerhof functional, PBE [11]). To take into account the van der Waals interactions, we utilized the Grimme semi-empirical corrections, DFT-D2 [12] and DFT-D3 [13]. For the SIESTA calculations, pseudopotentials were taken from the FHI database [14] and [15], for the VASP simulations, we used the 2012 version of pseudopotentials, with 2s22p2 electrons for С as valence.

The simulation cell contained 64 carbon atoms (32 for each graphene layer). The optimized translational parameter was 9,86 Å and 9,79 Å for GGA (GGA+D) and LDA calculations, respectively. We chose the partitioning density of the reciprocal space (k-points) and the real space (the MeshCutoff parameter in the SIESTA package and the Accurate tag in the VASP code) so that the precision of the structure's total energy was ~1 meV. For VASP, the cutoff energy of plane waves was taken as 600 eV. Simulation parameters are presented in Table 1. For one graphene layer, we performed both spin-polarized and not spin-polarized calculations. However, the difference between the resulting total energies was less than 1 meV. Therefore, the bilayer systems we modeled without spin polarization to save computer resources. The resulting precision of the interlayer binding energy was about 0,3 meV/atom.

Table 1

Simulation parameters

DFT package	SIESTA	VASP
XC approximations	PBE-GGA, CA-LDA, PBE+D2	PBE-GGA, CA-LDA, PBE+D2, PBE+D3
k -points	19×19×1	9×9×1
Space partitioning (mesh detailing in the real space): MeshCutoff (SIESTA) / PREC (VASP)	GGA (+D2): 360 Ry; LDA: 230 Ry	Accurate
Total energy convergence criterion	10–6 eV	10–6 eV
Force convergence criterion	10–4 Ry/Bohr	10–3 eV/Å
Vacuum layer in the direction perpendicular to graphene, Å	at least 20	at least 20

Basis set optimization

We optimized the localized pseudoatomic orbitals of the carbon atom according to the procedure described in [16]. To minimize the computational time, we simulated the graphene primitive unit cell, which contains only 2 carbon atoms. The cell translation parameter was 2,47 Å, the simulation parameters were the same as in Table 1, except for k -points: in this case, we used a 32×32×1 set. Since the unit cell is small, instead of the interatomic distance, we checked the system “pressure” which indicates how far the translational parameter of the simulation cell, and hence the distances between carbon atoms, are from optimal.

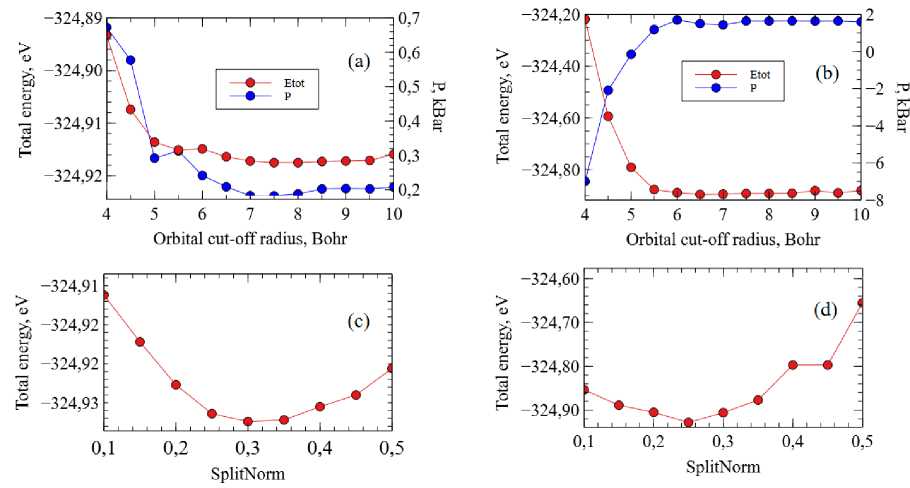
Fig. 1. Optimization of C(2p) and C(2s) orbitals for SIESTA calculations (GGA-PBE). Dependences of the total energy and pressure on the orbital cut-off radius of: (a) C(2s) and (b) C(2p) orbitals; dependence of the system total energy on the parameter SplitNorm for: (c) C(2s) and (d) C(2p) orbital

Figure 1 shows the results of orbital optimization for graphene, simulated with GGA. The used double-ζ basis set could be characterized by two parameters: the orbital cut-off radius, r , and the SplitNorm parameter, which specifies the radius of the modified orbital, r [8]. The optimal parameters were chosen using the criterion of minimal total energy, while the pressure of the simulation cell was additionally monitored. Fig. 1a indicates that both system total energy and pressure were at approxi- Вестник ЮУрГУ. Серия «Математика. Механика. Физика»

2022, том 14, № 2, С. 64–71

mately the same level after the C(2s) orbital cut-off radius reached ~7 Bohr. Since for a larger r more computer resources are needed, we chose r = 7,0 Bohr as optimal. The dependence of the total energy on the SplitNorm parameter had a pronounced minimum at SplitNorm = 0,30, which was chosen as optimal. The optimal parameters of С(2р) orbital were determined similarly (see Fig. 1, b , d ). Optimal basis-set parameters are presented in Table 2.

Table 2

Optimal basis set parameters for C(2p) and C(2s) orbitals, 1 Bohr ≈ 0,529 Å

XC approximation	GGA and GGA+D			LDA
Orbital	rcut , Bohr	SplitNorm	r Bohr m ,	r Bohr cut ,	SplitNorm	r Bohr m ,
Pseudopotential from [14
C(2s)	7,09	0,30	2,95	7,09	0,30	2,95
C(2p)	6,57	0,25	3,18	6,57	0,25	3,18
Pseudopotential from [15
C(2s)	6,57	0,25	3,11	7,09	0,30	3,03
C(2p)	7,09	0,25	3,22	6,57	0,25	3,18

Table 2 shows that the optimal parameters in the case of different XC approximations (GGA and LDA) practically coincide and are close for the chosen pseudopotentials.

Geometry optimization of different BLG configurations

After basis-set optimization, we investigated the structure of bilayer graphene using the SIESTA package. We considered starting configurations with various relative displacements in three directions of one graphene layer to another. The interlayer binding energy was calculated as:

E = E - 2 E - E ,                          (1)

bind       2l        1l      CP , where E and E are the total energies of the bilayer system and the isolated layer, respectively, and

E is the Boys–Bernardi correction to the basis set superposition error [17].

Firstly, we shifted the second layer only along the Z-axis (AA structure, Fig. 2a). We tested different initial shifts (from 1 to 15 Å). Though, at ∆z ≥ 10 Å ( ∆z ≥ 5 Å for PBE-GGA calculations) the layers did not interact: the interlayer distance, d , did not change after geometry optimization, and the interaction energy E = 0 eV. All other initial structures moved to a stable state with a certain minimum in- terlayer distance (this distance varied depending on the used XC approximation, see Table 3).

At the next stage, we added a shift along the X -axis. The initial interlayer distance was taken from the stable AA configuration. We considered the initial shifts ∆x in the range of 0,2–0,8 Å (with a step of 0,2 Å). After geometry optimization, we got either the A(B) configuration (Fig. 2, b ) or AB (Fig. 2, c ). In the case of SIESTA DFT-D2 calculations, we observed only the AB . Finally, when a shift along the Y -axis was added (we considered the same initial shifts ∆y as ∆x ), all starting structures transferred to the AB configuration. The obtained values of the interlayer distances and the interlayer binding energies for SIESTA and VASP calculations are presented in Tables 3 and 4, respectively. The values in parentheses (Table 3) show the results obtained with the pseudopotential from [15].

Fig. 2. Atomic structure of the (a) AA system (shift along the Z -axis); (b) A(B ) system (shifts along the X- and Z- axes), and (c) AB system (shifts along the X- , Y- and Z -axes)

Table 3 shows that the GGA calculations predict the weak interaction of the layers or even their repulsion. In previous theoretical studies with various dispersion corrections (including quantum Monte Carlo and DMC methods), the BLG interlayer binding energy for the АА-structure was in the range of 10,4–31,1 meV/atom; for the АВ-structure – in the range of 17,8–70,0 meV/atom [18]. Experimental values for the graphite interlayer binding energy are also very scattered: 0,21–0,37 J/m2 (indirect measurements) and 0,19 J/m2 (direct measurements) [19].

Table 3 The interlayer binding energy, E , and distance, d , calculated using the SIESTA package

Structure	AA			A(B)			AB
XC functional	PBE	CA	PBE+D2	PBE	CA	PBE+D2	PBE	CA	PBE+ D2
d , Å	3,73 (4,02)	3,44 (3,45)	3,38	3,53 (3,55)	3,25 (3,23)	—	3,49 (3,48)	3,23 (3,23)	3,17
| d - d exp | , Å	0,18 (0,47)	0,11 (0,10)	0,17	–	–	–	0,14 (0,13)	0,12 (0,12)	0,18
— Е bind , meV/atom	–1,8 (–5,7)	19,2 (19,1)	41,6	–1,9 (–2,3)	26,8 (28,3)	–	–1,8 (–3,2)	28,1 (28,3)	54,1
– Ebind , J/m	–0,01 (–0,03)	0,12 (0,12)	0,25	–0,01 (–0,01)	0,17 (0,18)	–	–0,01 (–0,02)	0,17 (0,17)	0,33

We chose the empirical graphite interlayer binding energy for comparison because the calculated interlayer E for graphite and BLG are close [20]. Experimentally obtained BLG interlayer distances are 3,55 Å and 3,35 Å for AA and AB configurations, respectively [1]. Therefore, LDA predictions for both the BLG interlayer binding energy and distance are closer to the experimental data than GGA values, although PBE-D2 binding energies are also close to previously obtained experimental and calculated values. Moreover, the difference in the calculation results obtained for considered pseudopotentials was within the calculation error.

Table 4 The interlayer binding energy, E , and distance, d , calculated using the VASP package

Structure	AA				A(B)				AB
XC functional	PBE	CA	D2	D3	PBE	CA	D2	D3	PBE	CA	D2	D3
d , Å	4,50	3,60	3,52	3,71	4,39	3,36	3,29	3,55	4,38	3,32	3,25	3,53
| d - d exp | , Å	0,95	0,05	0,03	0,16	–	–	–	–	1,03	0,03	0,10	0,18
— Е bind , meV/atom	1,1	14,9	38,7	39,1	1,3	22,9	48,8	43,5	1,3	24,5	50,6	44,1
– Ebind , J/m2	0,01	0,09	0,24	0,24	0,01	0,14	0,30	0,26	0,01	0,15	0,31	0,27

The VASP simulations (Table 4) also show that the optimal approximation for studying bilayer graphene is LDA. DFT-D3 corrections tend to predict weaker interlayer binding and larger interlayer distances than DFT-D2. The used simulation packages gave similar results: the difference in binding energies while using the same XC approximations was only 3–4 meV/atom. We observed the smallest difference in the interlayer distance predictions for LDA and DFT+D2 approximations (it did not exceed 0,16 Å, which corresponds to ~4 % difference). The maximum distance variations were observed for GGA-simulated AB configuration: the VASP results exceeded the SIESTA values by 0,9 Å (which corresponds to more than 25 % difference).

Conclusion

In this work, we obtained the optimized model of bilayer graphene and studied its structural and energetic features using the electron density functional method implemented in the VASP and SIESTA packages. For the SIESTA calculations, we optimized the parameters of localized pseudoatomic orbitals for carbon. After the geometry optimization of BLG, we observed a stable Bernal structure ( AB configuration) with a minimum total energy and two metastable structures: AA and A(B) configurations.

The comparison of BLG interlayer binding energies and distances showed that the results obtained by different packages (SIESTA and VASP) were consistent after the simulation parameters optimization (including basis sets) and taking into account the basis set superposition error. Finally, the best agreement with the available experimental data was obtained for the local electron density approximation. Grimme corrections gave the interlayer binding energy close to some experimental results for graphite, too, but its geometrical predictions for the most BLG configurations were less accurate than LDA values. GGA is not suitable for BLG simulation since its application resulted in non-interacting or repulsive layers.

The reported study utilized the supercomputer resources of South Ural State University [21] .