Ab initio studies of hydrogen physisorption on clear and Li-doped carbon nanotubes

Hydrogen is considered as one of the most perspective energy carriers as it has a high energy content per mass, it can be generated from clean and green sources and its combustion produces only water as a byproduct [1]. However, for the utilization of H 2 in the national energy systems the difficulties concerning storage and transporting of hydrogen fuels should be overcome.

These problems can be solved by using compact and safe hydrogen storages. To create such storages it is necessary to find appropriate hydrogen sorbent. Carbon-based nanomaterials are thoroughly investigated candidates for H 2 storage due to their low density, porosity, high thermal and chemical stability, the simplicity and low cost of production [2]. Carbon nanotubes (CNTs) have not only properties mentioned above but also high mechanical strength, unique electrical and capillary features and therefore they attract a great attention of researches [3]. However, in spite of high surface area clear CNTs can adsorb only up to 1 wt % at room temperature [4] due to the weak bond between H 2 molecules and tube [5].

The possible solution of this problem is more active adsorption sites formation, for instance, by doping of carbon nanotubes with metal atoms [6, 7]. The perspective element for such use is lithium, because it has high nucleation barrier [8, 9]. Recently, Li-doped CNTs have been investigated theoretically and experimentally in search of effective material for Li-ion battery [10, 11]. Much less is known about the interaction of these structures with hydrogen. To fill this knowledge gap ab initio modeling based on density functional theory of H₂ physisorption on clear and Li-doped carbon nanotubes was made.

Models and simulation details

To assess the effects of concavity and doping on hydrogen uptake and binding energy the adsorption on internal and external surfaces of clear and Li-functionalized CNTs of different radii was investigated. Density functional calculations were carried out using SIESTA code [12], where periodically boundary conditions are implemented.

As there is a risk of accumulation of static electricity in hydrogen storages in the sorp-tion/desorption processes, materials with high conductivity are required. Taking into account this fact, for modeling we chose armchair ( n , n ) carbon nanotubes that have metallic conductivity. These tubes also have small primitive unit cells that can decrease time costs of calculations.

In case of modeling Li-doped CNTs the distance between dopant atom and its image should be of the order of 10 Å, because at this extent valence orbitals of Li atoms do not overlap and the spurious interaction between lithium atom and its image can be excluded from consideration. This condition is fulfilled when the simulated fragment of nanotube has 4 or more CNT primitive unit cells.

The minimum CNT diameter D of approximately 7 Å was chosen not to have any steric or diffusion hindrances when placing lithium and molecular hydrogen into carbon nanotube [10]. In case of armchair tubes the value D — 7 A corresponds with n = 5. Also, wider (7,7) and (9,9) carbon nanotubes were investigated. The parameters of studied CNT models (the diameter D and the number of carbon atoms in the simulated fragment of the structure N_cell ) are indicated in Table 1.

We have performed density functional calculations with the local density approximation LDA (functional CA) and the generalized gradient approximation GGA (functional PBE). A basis set of atomic-like functions generated by Sankey scheme [12] was used. We simulated the rectangular supercells of

Table 1

The parameters of investigated CNT models

( n , m )	(5,5)	(7,7)	(9,9)
D , Å	6,78	9,49	12,20
N cell	80	112	144

dimensions about 100×100×10 Å3. The tube axis was directed along the shortest axis of the supercell. Massively larger supercell crosswise sizes excluded the possibility of the interaction between the CNT models and its images. The equilibrium length of simulated CNT fragments was determined by its optimization and differed by 1–2 Å for various systems. The optimization was made as follows: we calculated the dependence of system total energy Etot on the length l of the supercell shortest axis and the value corresponding to the minimal total energy was chosen as the equilibrium length of the model. Etot for every l was calculated by the optimization of other geometrical degrees of freedom. The convergence criteria for the force acting on atom constituted 0,1 mRy/Bohr. This choice of optimization parameter allows us to obtain good accuracy, further decrease of the convergence criteria for force acting on atom leads to a surge of computational time.

With DZP basis for all elements (H, C, Li), Meshcutoff [12] of 360 Ry for the GGA calculations and 210 Ry for the LDA calculations and the [1,1,32] Monkhorst–Pack set of k-points calculated energies have a numerical precision of 5–10 meV.

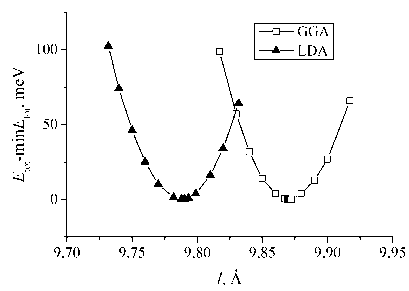
Fig. 1 presents the results of total energy calculations made with two approximations (LDA and GGA) in case of system CNT(7,7)@Li where Li is on the outside tube surface. We plotted not the values of total energies but the difference between system energy and its equilibrium total energy. This was done because modeling with various approximations for electron exchange-correlation interaction results in significantly different absolute values of total energy. CNT(7,7)@Li minimal E_tot constitutes –18 201,212 eV and –17 414,032 eV, in case of using the GGA and the LDA respectively. Fig. 1 shows that equilibrium length of CNT(7,7)

Fig. 1. The dependence of CNT(7,7)@Li total energy on the length of supercell shortest axis. Calculation were made with the local density and the generalized gradient approximations. Li atom is outside the tube

and Li on its external surface calculated with the GGA constitutes 9,86–9,87 Å. In case of the LDA this length is about 9,78–9,79 Å. So, for system CNT(7,7)@Li the difference between equilibrium lengths computed with the GGA and the LDA is approximately 0,8 %.

Lithium adsorbtion on carbon nanotubes

The Li-atom was placed on top of a carbon hexagon. The binding energies E_bind were obtained by subtracting total energies as follows:

E bind = E CNT@Li - E Li - E CNT ,                                    ⁽¹⁾

where E_CNT@Li is the total energy of complex CNT+Li, E_Li is the energy of Li-atom and E_CNT is the energy of clear carbon nanotube.

Физика

Computed results for parameters of lithium adsorption on the modeled carbon nanotubes (the binding energy E_bind , the charge Q_tr transferred from Li-atom to nanotube and the distance d between Li and CNT surface) are presented in Table 2. The value of Q_tr was calculated according to Mulliken.

Table 2

Parameters of lithium adsorption on external and internal CNT surfaces

Approximation	GGA			LDA
Model	E bind , eV	Q tr , e	d , Å	E bind , eV	Q tr , e	d , Å
CNT(5,5)+Li inside	2,056	0,89	2,27	2,433	0,81	2,24
CNT(5,5)+Li outside	1,523	0,92	1,91	1,877	0,92	1,87
CNT(7,7)+Li inside	1,875	1,03	2,05	2,256	0,98	2,07
CNT(7,7)+Li outside	1,533	0,94	1,85	1,895	0,94	1,77
CNT(9,9)+Li inside	1,799	1,04	1.97	2,177	0,99	2,02
CNT(9,9)+Li outside	1,534	0,95	1,89	1,903	0,95	1,80

As one can see from Table 2, in all modeled cases the valence charge of Li almost completely transferred to carbon nanotube. The resulting electrostatic interaction between adatom and tube is the major contribution to the value of binding energy. The difference between adsorption parameters of internal and external sorption are great, especially if the CNT radius is small, like in case of CNT(5,5). This can be explained by the variations of overlaps of carbon and lithium orbitals when dopant atom is outside and inside the tube.

Hydrogen physisorption on pure carbon nanotubes

For modeling of adsorption of one hydrogen molecule initial configurations presented on Fig. 2

were chosen.

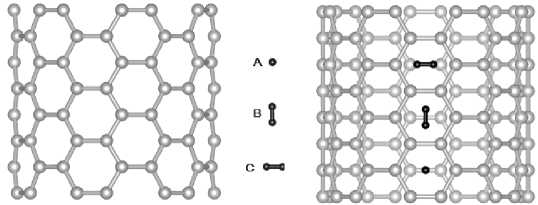
Fig. 2. Initial configurations of hydrogen molecules (A, B, C) related to the surface of CNT(7,7). In case of internal sorption the positions of configurations are similar

The binding energies E_ads of H 2 adsorption were obtained as follows:

E ads = E CNT@H - E H - E CNT ,   (2)

where E_CNT@H is the total energy of the complex CNT+H 2 , E_H is the energy of hydrogen molecule, E_CNT is the total energy of clean carbon nanotube.

For every initial configuration of hydrogen molecule the optimization of geometry with the above-mentioned convergence criteria for force acting on atom was made. The structure length was fixed. Eads and distance d between the nanotube surface and the mass center of H2 molecule computed with approximations GGA and LDA are indicated in Table 3.

Table 3

Parameters of hydrogen physisorption on pure carbon nanotubes

	Approximation	Configuration	(5,5)		(7,7)		(9,9)
			Eads , meV	d , Å	Eads , meV	d , Å	Eads , meV	d , Å
External adsorption	GGA	A	56	2,96	51	2,94	61	2,98
		B	56	2,97	51	2,95	56	3,02
		C	39	3,18	51 (B)	2,98	41	3,21
	LDA	A	138	2,58	164	2,55	188	2,59
		B	156	2,55	166	2,54	196	2,58
		C	152 (B)	2,57	180 (B)	2,53	167	2,73
Internal adsorption	GGA	A	252	3,36	137	2,96	120	2,90
		B	283	3,34	136	2,93	120	2,90
		C	282 (B)	3,36	113	3,11	93	3,04
	LDA	A	472	3,31	315	2,73	288	2,70
		B	476	3,31	322	2,71	287	2,69
		C	465	3,33	306 (B)	2,70	284 (B)	2,66

Sometimes the relaxation of the geometry led to a change in the orientation of the hydrogen molecule. In these cases new configuration (A, B or C, see Fig. 2) is marked in brackets in the column with values of Eads . As one can see from the Table 3, only molecules with the initial configuration C changed their direction. This configuration has smaller adsorption energy. The sign of CNT surface curvature significantly affects the hydrogen adsorption energy (the energy of internal sorption is 2–5 times higher than the energy of external sorption, and the bigger is the curvature the more considerable is the difference). Dependence of the binding energy on tube's radius is more discernible in case of internal adsorption (with the increasing of radius Eads reduces). When hydrogen molecules are outside the nanotubes the CNT radius has a small impact on the adsorption energy (with the increasing of radius Eads slightly rises or remains the same).

There is a tendency of the LDA to overestimate the energy of van der Waals interaction. In contrast, calculations with the GGA usually result in underrated energies of this weak interaction. So, the true value of E_ads is in the range of values obtained using these two approximations [13]. Finally, only in case of hydrogen sorption inside the CNT(5,5) energy of adsorption hit the range of 300–400 meV per molecule (see Table 3) that is necessary to have effective charging/recharging cycles in hydrogen storages [14].

To estimate the possible hydrogen uptake we considered the dependence of H 2 adsorption energy on number of hydrogen molecules in case of internal sorption on CNT(5,5). The adsorption energies of one H 2 molecule were calculated as follows:

E ads = ⁽ E CNT@nH - E nH - E CNT )/ n , (3)

where n is a number of H₂ molecules in simulated complexes, other notations are similar to ones in the Formula (2).

When n >  2 there are several equilibrium configurations where hydrogen molecules get into different positions in relation to each other and the CNT surface. Near the configuration with the lowest energy usually there are some other configurations with the close energies. Table 4 presents the results

of calculations of binding energies in case of n = 2 ^ 6. For every n it indicates the range of Eads of configurations that are close to the energetically most favorable one. As one can see from Table 4, only in case of internal sorption of up to 4 hydrogen molecules on 4 primitive unit cells of CNT(5,5) energy of adsorption hit the desirable range. But in this case hydrogen uptake is too low and constitutes about	Table 4 Adsorption energy E ads (meV) of H 2 molecules inside CNT(5,5)
	Число молекул	Приближение
		GGA	LDA
	2	250-269	464-479
	3	241-244	448-450
	4	205-215	399-401
	5	133-134	354
	6	94	330

1,6 wt %. This fact confirms the inefficiency of clean carbon nanotubes as hydrogen storages under ambient temperature and pressure.

Hydrogen physisorption on Li-doped carbon nanotubes

For modeling of adsorption of one hydrogen molecule on complexes CNT+Li (H2 and Li are at the same side of nanotube surface) initial configurations presented on Fig. 3 were chosen. The position A is near lithium and on top of a neighboring carbon hexagon. In the orientation A1 the molecule axis is parallel to the tube's surface and perpendicular to the tube's axis, in A2 it is parallel to both tube's surface and axis and in A3 it is perpendicular to the nanotube surface. The position B is on top of Li-atom. The site B1 is similar to A1, B2 is similar to A2. The position C is like A, but it is placed

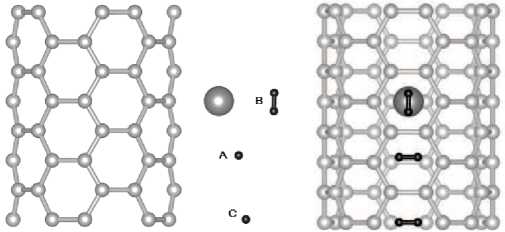
Fig. 3. Initial configurations of hydrogen molecules (A,B,C) related to the surface of CNT(5,5)@Li. In case of internal sorption the positions of configurations are similar

father from lithium. The orientation C1 is similar to A1, C2 is similar to A3. In case of internal sorption notations are the same.

Физика

For every initial configuration of hydrogen molecule the optimization of geometry with the abovementioned convergence criteria for force acting on atom (0,1 mRy/bohr) and the fixed structure length was made.

The adsorption energy of hydrogen E_ads was obtained by subtracting total energies as follows:

Eads = ECNT@Li@H EH ECNT@Li, where ECNT@Li@H is the total energy of the system CNT+Li+H2, EH is the energy of hydrogen molecule and ECNT@Li is the total energy of the complex CNT+Li.

Also we calculated the distance between Li-atom and the mass center of H₂ molecule d_H-Li and the distance between this mass center and the CNT surface d_H-CNT . Results of modeling are presented in Table 5.

Table 5

Parameters of hydrogen physisorption on Li-doped carbon nanotubes

	о E X о	s .s о и	(5,5)			(7,7)			(9,9)
			Eads , meV	d H-Li , Å	d H-CNT , Å	Eads , meV	d H-Li , Å	d H-CNT , Å	Eads , meV	d H-Li , Å	d H-CNT , Å
a о & о 'cd E о X M	О	A1	137	2,28	3,08	142	2,29	3,06	149	2,28	3,05
		A2	146 (A3)	2,25	3,24	151 (A3)	2,25	3,20	154 (A3)	2,24	3,21
		A3	146	2,25	3,23	150	2,23	3,20	155	2,23	3,23
		B1	147	2,23	4,06	146	2,22	4,07	142	2,23	4,10
		B2	147	2,21	4,05	148	2,22	4,06	141	2,23	4,10
		C1	53	5,06	2,96	60	5,05	2,95	59	5,04	2,96
		C2	48	5,11	3,15	51	5,10	3,14	53	5,09	3,17
	< Q	A1	249	2,30	2,56	258	2,28	2,54	258	2,29	2,54
		A2	252 (A3)	2,21	2,71	264 (A3)	2,23	2,59	265 (A3)	2,20	2,68
		A3	252	2,22	2,69	258	2,20	2,69	259	2,20	2,71
		B1	216	2,13	3,89	178	2,14	3,90	183	2,14	3,92
		B2	170	2,14	3,90	178	2,13	3,89	184	2,14	3,91
		C1	145	4,97	2,57	158	4,97	2,55	164	4,95	2,56
		C2	131	4,99	2,69	159 (C1)	4,96	2,56	150	4,98	2,69
a о & о 'cd E У	S О	A1	274	2,27	3,47	200	2,26	3,05	193	2,27	2,98
		A2	274 (A1)	2,27	3,47	196 (A3)	2,25	3,23	194 (A3)	2,27	3,02
		A3	273	2,27	3,43	196	2,25	3,23	194	2,26	3,02
		B1	274 (A1)	2,27	3,47	182	2,22	4,28	172	2,21	4,18
		B2	272 (A1)	2,27	3,46	173	2,22	4,27	167	2,21	4,17
		C1	237	5,09	3,38	134	4,98	2,96	115	5,02	2,89
		C2	253	5,11	3,36	134 (C1)	4,98	2,96	101	5,05	3,03
	< Q	A1	510	2,26	3,13	365	2,25	2,69	340	2,25	2,65
		A2	510 (A1)	2,26	3,13	364 (A3)	2,23	2,70	334 (A3)	2,25	2,65
		A3	505	2,28	3,38	364	2,23	2,70	333	2,17	2,74
		B1	510 (A1)	2,26	3,13	254	2,12	4,18	212	2,11	4,10
		B2	473	2,05	2,61	243	2,13	4,18	207	2,11	4,10
		C1	475	5,03	3,35	292	4,94	2,69	261	4,94	2,65
		C2	457	5,05	3,38	259	4,95	2,78	225	2,96	2,75

Comparing Tables 3 and 5 one can see that doping with Li atom increases the adsorption energy of hydrogen molecules up to 30–100 meV. The lowest impact is in the case of internal adsorption (especially inside narrow CNTs). The binding energy between H 2 and CNT(5,5)@Li is about 10 % higher in comparison with pure CNT(5,5). In case of wider CNT(9,9) this value achieves approximately

• 30 %. The binding energy of hydrogen to external nanotube's surface increases by 2–3 times but remains insufficient for practical uses. Dependence of adsorption energy on tube's radius is more discernible in case of internal adsorption: when passing from a narrow (5,5) tube to (9,9) a nanotube the energy drops by a factor of 1,5. The binding energy of hydrogen to external CNT's surface becomes slightly greater with tube's radius increasing.

To summarize, doping of CNTs with lithium can increase the adsorption energy of hydrogen molecules by several times in comparison with the clean CNTs. Nevertheless, the optimal range of binding energy 300–400 meV per H 2 molecule can be achieved only in case of hydrogen adsorption inside quite narrow (5,5) and (7,7) Li-doped nanotubes.

Conclusions

Modeling of the selected systems CNT+H 2 and CNT+Li+H 2 showed that pure carbon nanotubes can adsorb only small amount of molecular hydrogen (up to 1,6 wt % in case of internal sorption on (5,5) nanotube) due to the weak bond between H₂ molecules and tube. Doping with Li atom increases the adsorption energy of hydrogen molecules up to 30–100 meV because of the contribution of electrostatic interaction (the valence charge of Li almost completely transferred to carbon nanotube).

The curvature of nanotube surface significantly influences the energy of the internal sorption of hydrogen while the effect on the external sorption is of minor importance both in case of clean and doped nanotubes. When hydrogen molecules are inside the tubes the binding energies are 1,5–3,5 times bigger than when these molecules are outside. With the increasing of the CNT radius this difference reduces.

On the whole, despite the fact that in case of external sorption doping with Li-atom can increase the adsorption energy of hydrogen molecules by several times in comparison with the clean CNTs, only inside quite narrow (5,5) and (7,7) Li-doped nanotubes the values of binding energies can hit the desirable range. However, small radius of these tubes can lead to low hydrogen capacities because of the problems with the diffusion accessibility of the inner surface of the tubes.

The reported study utilized the supercomputer resources of South Ural State University [15].