ABC Algorithm Based Interval Type-2 Fuzzy Logic Controller for an Inverted Pendulum

The cart type inverted pendulum system is a multivariable,nonlinear, fast reaction, unstable and high order system. It is a classical control problem that is used by many researchers to design and test control technique. [1,2].

For an inverted pendulum cart, a number of research works previously exist in the literatures that make use of control techniques.

A number of types of controllers are accessible for designing, analyzing and controlling the inverted pendulum both linear and non-linear dynamic deviations. Like PI controller, fuzzy controller, optimal controller and etc. However, these kinds of controllers are incompetentas they need a large number of equations and control methods. For linear control problem only the PI controller is appropriate. The PI increase tuning is one of the complex problems in nonlinear control problem. For controlling the nonlinear dynamic difference of the system, the fuzzy logic controller is a rule base control method that is used. Although, in rule base controller, the rules obstruction problem has to be happened that affected the control presentation of the system. Moreover, these kinds of controller are controlled by only one control parameters (arm angle, pendulum angle, arm velocity and pendulum velocity) of the system. In order to control the angle and velocity variation of the inverted pendulum, a hybrid control technique is proposed in this paper. The proposed technique is detailed in following section.

The rest of the paper is organized as follows. In section II modeling of inverted pendulum is shown. Proposed hybrid controller for improving velocity and angle of inverted pendulum is discussed in section III. It also includes detailed discussion of ABC algorithm to optimize the pendulum angle and velocity and how to controlthe pendulum angle and velocity using IT2FLC with the complete procedure. In section IV results and discussion are given with performance analysis of change in angle and velocity of Inverted Pendulum. Finally conclusion is presented in section VI.

• II.    Modeling of Inverted Pendulum

The inverted pendulum system is one of the examples which commonly used in control system application. The reputation of the drives in part from the fact that it is unstable without control. Because, the pendulum will simply fall over if the cart isn't moved to balance it. In addition, the dynamic states of the system are nonlinear. The intention of the control system based controller is to balance the inverted pendulum by applying a force to the cart that the pendulum is attached. [3]. It consists of an inverted beam (pole) on a moving cart as shown in Figure1. The task of the controller is to stabilize the pole angle ( θ ) and the cart position (x) by applying the force

(F). The configuration and the free body diagram are illustrated in Figure1(a) and Figure1(b) respectively.

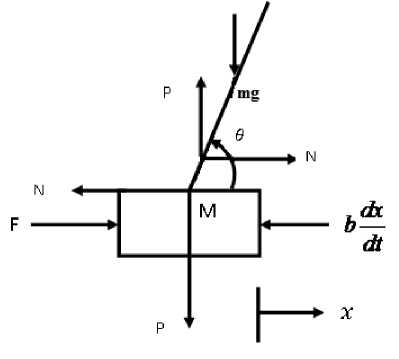
Fig. 1(a). Configuration of Inverted pendulum

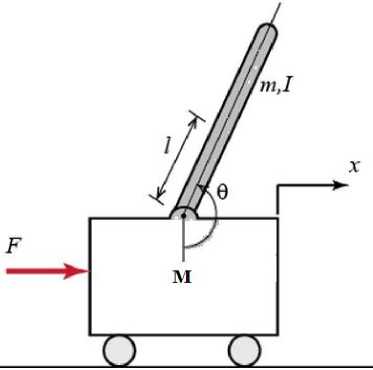
Fig. 1(b). Free body diagram where F is the control (applied force), x is the displacement of the cart, theta is the angle of the with respect to the vertical axis, (A^) indicates the pendulum deviation position from the equilibrium position i.e. ; g = 9.8m/s2 is gravity acceleration. Other parameters are the mass of the cart M = 0.455Kg, mass of the pole m=0.21 Kg; the friction coefficient b = 0.1N/m/sec ; distance to pole centre of mass l = 0.3m; the inertia of the pole I =.0035Kg.m2 The governing equation of the system is described as follows,

,d2x2 ml—— = (I + ml I - mglф dt2

d2x , dx

(M + m I + b - ml = 0 dt 2 dtdt

The above mathematical derivations are used to model inverted pendulum. For controlling the angle and the velocity of the pendulum, the IT2FLS is used.

The proposed hybrid controller structure shown in Figure 2 is used for controlling the angle and the velocity of the pendulum. An artificial bee’s colony (ABC) algorithm[3] is used for optimizing the input membership function of fuzzy inference system.

• III.    Proposed Hybrid Controller for Improving the Velocity and Angle of Inverted Pendulum

• 3.1    Using ABC Algorithm to Optimize the Pendulum Angle and Velocity

Initially, the angle and velocity of the inverted pendulum are evaluated. After that, the change in the velocity and the change in angles are determined by taking the difference between the present and earlier error. By applying these changes of angle and change of velocity as the input to the IT2LS, the control output is calculated. Before giving the inputs to the IT2FLS, the change of angle and the change of velocity are optimized by using ABC algorithm and the optimized membership functions are generated from the obtained optimized output of ABC algorithm. [4]The objective function of ABC algorithm is depends on the control output of the IT2FLS. The proposed hybrid controller block diagram is illustrated in fig 2. The detailed description of the proposed hybrid technique is explained in below section.

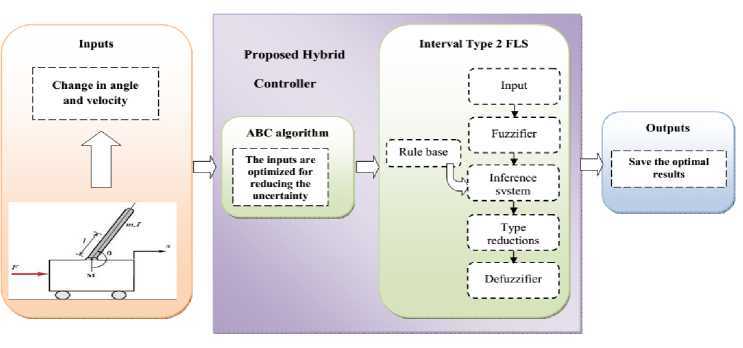
Fig. 2. Structure of proposed hybrid control model

ABC algorithm is a swarm based meta-heuristic algorithm[4] which was stimulated by the sharp foraging behavior of the honey bees. Employed bees, onlooker bees and scout bees are the three components of ABC algorithm. The number of food sources indicates the position of possible solutions of optimization problem and the nectar amount of a food source indicates the excellence of the solution [5]. In this section part, the change of angle ( A ^ ) and the change of velocity ( A v ) of the pendulum are optimized by using ABC algorithm. The optimized inputs are applied to the IT2FLS and the optimized membership function is generated. The procedures of the ABC algorithm is specified as follows,

Steps for ABC algorithm

Step 1: Initial phase

The change of angle ( AO - ) and velocity ( a v i ) of inverted pendulum are considered as the parameters of the food sources in the population, which are generated arbitrarily. The random number of the population is X i e ( A0 _t, A v i ) , where i = 1,2,... N and N denotes the size of population. This generation process is called as initialization process.

Step 2: Fitness Function

To evaluate the optimal parameter of the inverted pendulum, the fitness value is calculated using equation (1),

Fitness function F- = min ( a ^ -, A vi )

After that, the phase of the employed bee is carried out.

Step 3: Employed bee phase

Update the velocity and angles of pendulum positions using the following equation,

Y i, j = X i , J +^ ij ^{( X}i , j - ^Xk , j )                (4)

Where, Y is the new value of the j ^th position and k , j is a random selected index. Here, ф is randomly produced the number in the range [-1, 1].

Then evaluate the fitness values and apply the greedy selection between them Y and x _{i ,} j . Determine the probability values for the solutions X _{i ,} j by means of their fitness values using the following equation,

F i

Pi     d                                               (‘

z Fi                          ( i=1

Where p is the probability of the i^th parameter value.

Step 4: Onlooker bee phase

Generate the new solutions or positions Y for the onlookers from the solutions X i , selected depending upon the probability value p and calculated them. Then, the fitness function is calculated for the new solutions. In order to select the best value, apply greedy selection for the onlooker bee between X_i and Y .

Step 5: Scout bee phase

In this section, the abandoned solution, if exist, and replace it with a new randomly produced solution.

Memorize the best food source position achieved. The particular parameter value has been selected as the optimal value. The above process is repeated until the maximum iteration is reached otherwise the process is terminated. The flowchart for the proposed ABC algorithm is illustrated in Fig. 3.

• 3.2    Controlling the Pendulum Angle and Velocity

Using IT2FLS

For stabilizing the inverted pendulum model, the fuzzy logic controller [6] is to be considered. Here, IT2FLS is used for In the IT2FLS, the rule base part enclosed with antecendents and consequents parts and each rule inference output is a type-2 fuzzy set.

The membership function limits are chosen with the help of the optimal velocity and the controlling the inverted pendulum angle and the velocity with minimum control deviation.

T2FIS is a fuzzy logic system, which contains fuzzifier, rule base, inference engine, type reductions and defuzzifier [7].optimal angle[8]. It is used for reducing footprint of uncertainties (FOU)[9]. A uniform weighting is supposed to symbolize a FOU since the mean changeable between m1 and m2, the gaussian function is measured with a standard deviation. The structure of the propsoed IT2FLS is given in figure4.

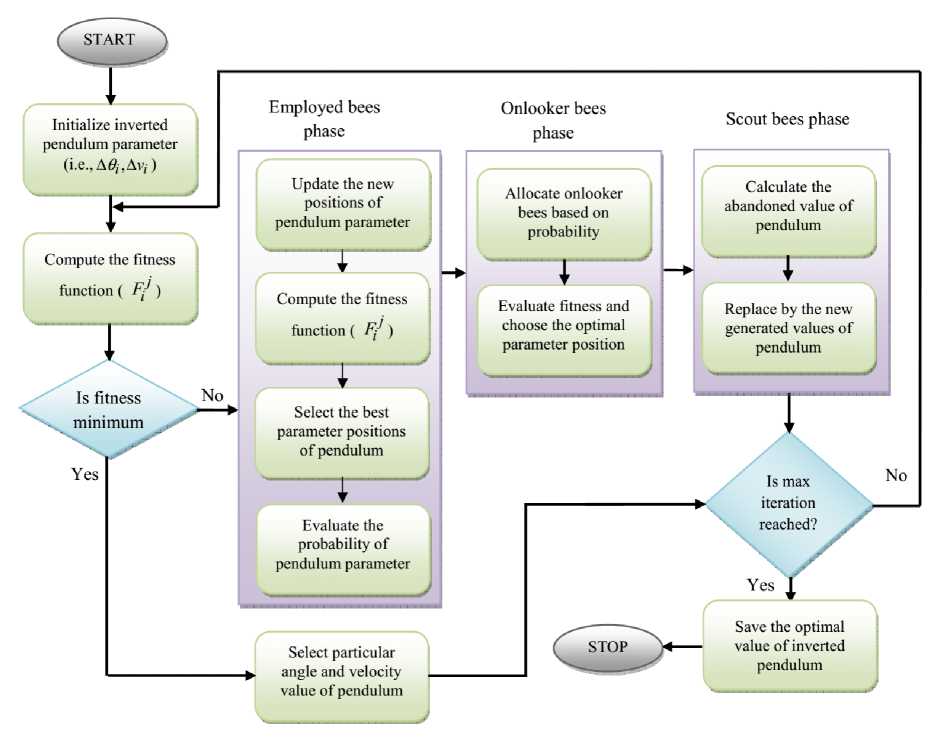
Fig. 3: Flowchart of the ABC algorithm for optimizing the inverted pendulum parameters deviation

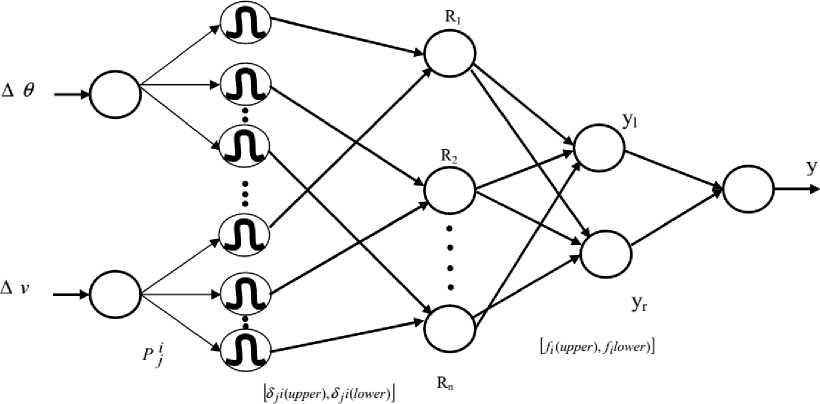
Fig. 4: Structure of proposed IT2FLS

• 3.3    Procedure of IT2FLS

Step 1: Fuzzification

Fuzzification

It is the first step of the IT2FLS, which converts the crisp parameters of input Δθ and Δv are fuzzified into input interval type-2 fuzzy sets. In fuzzification, the change of angle and change of velocity are maps to the linguistic labels of fuzzy sets. [10] The membership functions of these fuzzy sets contain two inputs and one output. Here, the input vector is Xi =(xj, x2, xn) and the if-then rules are specified in the following,

F =⁽ fl ^{( lower} ) , ft ⁽ upper )

Where,

Rlt = If xt is p AND x is P‘AND xnis PniThenY isa

Where, P j are the antecedents j = 1,2,3... n and Y i is the consequent of the i ^th rule. Then the Gaussian membership function (MF) is used which has a fixed standard deviation (SD) and uncertain mean that takes in the values in [ m j -j , m j 2 ] . The uncertainty of this membership functions can be represented in the bounded interval in terms of upper MF and lower MF. The Gaussian membership functions with uncertain mean described as,

n fi(upper) = ПDi (upper) j=1

n fi (lower) = J nDi (lower) j=1

r

к

D j ( X j ) = exp

к

Step 3: Inference Engine

After obtaining the firing strength, the inference engine and the rule base are activated by the interval type-2 fuzzy sets to produce output. Then the input interval type-2 fuzzy sets and output interval type-2 are mapped by combining the fired rules using inference engine. Then outcome of the inference engine are processed by the type-reducer. The type-reducer combines the output sets and performs a centroid calculation which leads to type-1 fuzzy sets called the type-reduced sets.

Where, m j e [ m j -j, m j 2 ] and j = 1,2,3... n , n is the number of antecedents. Then the i = 1,2,3... г , r is the number of rules. Then the upper and lower MF’s are specified as 5 j i ( upper) and 5 j i ( lower ) respectively and described in the (8) and (9).

T ^{( m}j P ^Dj ; ^xj )

X j <  m ii

3 j i ( upper) =

< 1      ^mj1 <  x j

T ( m p D j ; ^xj )

< j xj > mj 2

Step 4: Type Reductions

The type reduced set of the interval type-2 FS is an interval type1 set which contains the left limit yl and right limit yr[13]. The interval output of this layer is computed by each node present in this layer. The consequent a_i is a crisp value. Here we used a simplified type-2 reduction operation instead of the center-of-sets type reduction method. It considers only two embedded type-1 fuzzy sets with membership values, that is the outputs y^q and y^s are computed as follows,

and

S j i ( lower ) = -

^T ( m j 2 ,D i ^{; x}j ) ^xj

< mj 1 + m _г

M

^ ^f _t ( lower ) a i

^{T ( m}j 1 , D ; ^xj )    ^xj >

m j 1 + m j 2

y

q ₌ i =1

M

Where,output of the each node is represented as in the lower and upper interval.

y

^ fi(lower)

i =1

M

^ ft ⁽ uppera

q _ i = 1 M

Step 2: Rule base system

Here, the fuzzy meet operation is done by generating the rule [11,12].Two rules are generated by adding the upper membership functions seperately and lower membership function seperately for each node. The output of a rule node is a firing strength FSⁱ , which is an IT2 fuzzy set. The firing strength is computed as follows,

^ ft ⁽ upper )

i = 1

After the type-reduction process, the type-reduced sets are then defuzzified.

Step 4: Defuzzification

Defuzzification is the last process of the IT2FLS where each output node corresponds to one output variable. Due

to the output layer of an interval set, each and every node performs defuzzification process[14]. The defuzzified output is denoted by y which is determined by taking the average of the nodes y^q and y^s .

, = y q + y s

Subsequently the obtained defuzzified control output of fuzzy system is given to inverted pendulum to reduce the deviations of the angle and the velocity of the pendulum and also the position of the pendulum are maintained that was close to the reference position.

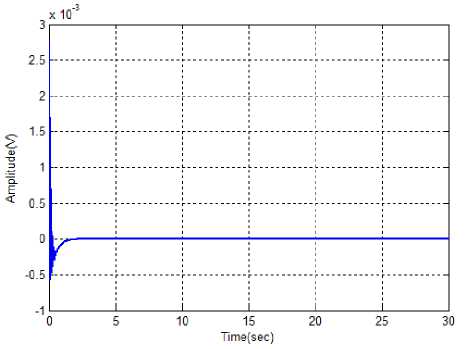
Fig. 5(a): Performance of change of angle of inverted pendulum

• IV.    Results and Discussion

• 4.1    Performance Analysis

0.06

0.04

0.02

s

CD

0

-0.02

-0.04

i                                          i                                          i                                          i

_

-0.06

5         10        15        20        25        30

The proposed hybrid technique was implemented in MATLAB/simulink working platform. The performance of the proposed hybrid technique was tested with inverted pendulum cart system. By using ABC algorithm, the optimal velocity and the angle parameters of the pendulum was determined. Here, the change of velocity and angles are calculated from their difference between the present state error and the previous error. This error function was set as a fitness function of the ABC algorithm. The minimum value of the fitness function is evaluated. After that, the optimized outputs are given to the IT2FLS. In the IT2FLS, the uncertainties are reduced and the optimal membership functions are determined. By using IT2FLS, the control output is generated for the inverted pendulum, which is controlling the angle and the velocity also, the stability position of the pendulum are determined. The performances of the proposed hybrid technique are evaluated.

Initially, the angles and velocity of the inverted pendulum performances are evaluated in normal position and illustrated in fig 5(a) and 5(b) respectively. Then applying the ABC algorithm, the input of IT2FLS is optimized in terms of control output12]. The output of ABC-IT2FLS is applied to the pendulum for controlling the angle and velocity. Then, the angle and velocity of the pendulum is observed after applying the ABC-IT2FLS. After that, the performances of the proposed method are evaluated and illustrated in the fig 6(a) and 6(b).

Time(sec)

Fig. 5(b): Performance of change of velocity of inverted pendulum

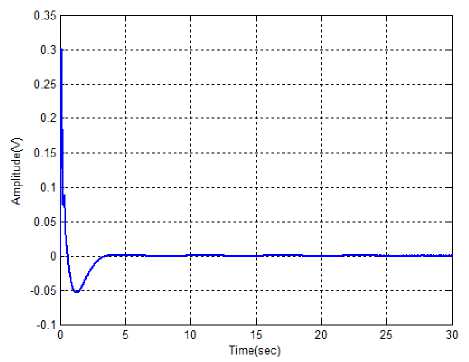
Fig. 6(a): Performance of pendulum angle using proposed hybrid controller

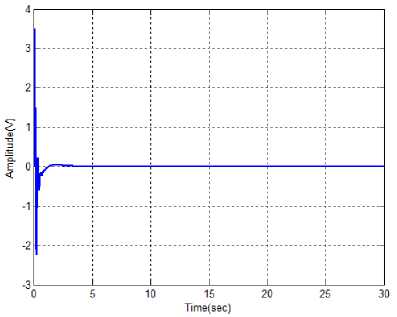
Fig. 6(b): Performance of pendulum velocity using proposed hybrid controller

From the above illustrations, the optimal value of pendulum angle and velocity are measured with the different time instants. Here, the various methods are used to calculate the optimal value of angle and velocity. The proposed hybrid controller achieves less time for optimizing the pendulum angle and velocity.

Here, the peak value and peak time is not varied for most of these methods. The settling time of the proposed controller is 2.9800sec. So, the proposed controller reaches the settling time to take very less time. The proposed method reaches the actual system state very quickly. Also, the proposed control technique maintains the system stability while changing the system mass.

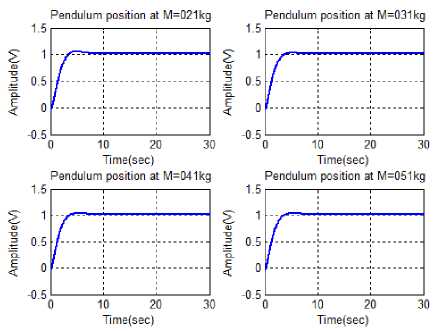
Fig. 9: Performance of cart position using proposed hybrid controller at M=0.21Kg, 0.31Kg, 0.41Kg, and 0.51Kg

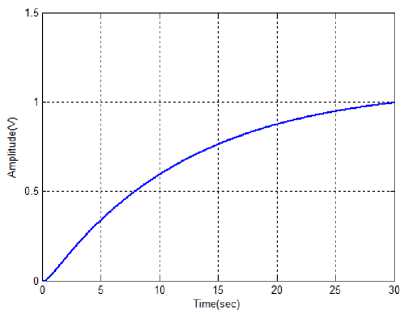
Fig. 7: Performance of normal cart position

By using the proposed hybrid method, the stability cart position of the pendulum is analyzed. The performance of cart position after applying the proposed hybrid control approach is described in Figure 8. Then, the stability of the proposed controller is analyzed at different pendulum mass values that are M=0.21kg, 0.31kg, 0.41kg and 0.51kg respectively. The performance of cart position at different pendulum mass value is described in Fig 9. Therefore, the stability of the cart position is steadily preserved in the proposed hybrid method

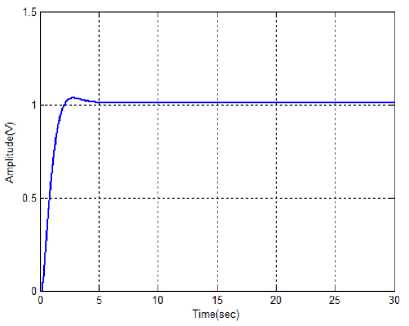
Fig. 8: Performance of cart position after applying proposed hybrid controller

The performance of the normal cart position is illustrated in the figure7. After applying hybrid controller the cart positions is shown in fig 8 respectively.

• V.    Conclusion

In the paper, a hybrid control technique was proposed for controlling the angle and velocity of the inverted pendulum. The proposed hybrid technique was implemented in the MATLAB/Simulink platform. The ABC algorithm was used to optimize the change of angle and change of velocity of the inverted pendulum. By the optimized values, the range of fuzzy membership function was selected. Hence, the control performance of the IT2FLS controller is improved and reduced the uncertainties. Also, the performance of the proposed controller is evaluated at different pendulum mass values.