About some properties and features of differential and integrated representations in the theory of thermodynamic functions

• 1.    Introduction

• 2.    Decision of the task

Thermodynamic functions are widely applied in the theory of metallurgical processes and in power system – [1 – 7].

At a conclusion of the equations for the isochoric – isothermal potential of F (Helmholtz’s energy) and the isobaric – isothermal potential of G (Gibbs’s energy) at the same time it is possible to allocate and distinguish two approaches. It is possible to call the first approach differential – [4-7], and the second approach – integrated – [8-12]. However in literature the distinctive and similar parties of these two aren’t considered and, differing approaches at a conclusion of the main equations for thermodynamic processes aren’t analyzed. In the present article we will carry out the analysis, theoretical justification and we will specify in what actually similarity and distinction of these two approaches at a conclusion of basic formulas for thermodynamic functions.

At the beginning we will consider a conclusion of the main equations on the basis of differential ratios, following results of works [3-7].

We will write down the first law of thermodynamics in a look dU-TdS-pdV.(1)

To both parts (1) we will add Vdp [4-7]

dU + Vhp = TdS - pdV + VPp .(2)

We will reurite (2) in the form of [4-7]

dU+ pd4+ 4dp = d(U + P4) = TdS + 4dp.(3)

From (3) follows that an enthalpу

P( )

is function of a c on dd ion of system a nd fun ctionof two independent variables [4-7]

dn = Tdp + Vdp.(5)

We subtract SdT from both members o f oq ua tioT (1) and we will write down it in the form of ^[4-^7]:

-SdT + dU-TdS = —pdV — SdT.

From (6) follows

d(U-TS) = -pdV-SdT.(7)

From (7) it is visible that size

F=U-TS(8)

is function of a condition of system (U, S) and full differential of some function which depends on two independent V and T vaaiables . da is function F is called isochoric-isothermal potential [4-7]

UF = -pUV - SUT.

Further, on the basi s o f thea n a lys is oft h e equation for full differential

-“’-69л+

Conclusion of the known formulas is made; for P, Ss C v ^- pl- 7].

We will consider an equation conclusion for isobaric and isothermal potential now. To both members of equation ⁽¹⁾ we will add the size ^(aap ^{- fan)} and we will write down ⁽¹⁾ in the form of _[4-7]

^oU + f^oq-T^oS + ^qoP-S^cT = ^qof-S^oT .                           (10)

From (10) after transformations wewill receive

^s(u ^- TS + P^q) = ^{SpC -} S^pT.                                            ⁽¹¹⁾

o  U U  T ЛПА

Follows from formulas (4) and (11) that

d(H - TS) = dG = VdP - SdT.                                         (12)

Therefore

G = H-TS                                            (13)

is function оf a condition of system and full differential of function from two independent variables p , T [4-7].

Useful formulas for V,S follow from the following formula for full differential - [3-7, 10]

dG = QTdo + Qp da.

From the above it is visible that for an enthalpy of H, izokhorno-isothermal F and isobaric and isothermal G potential, a conclusion on the basis of differential ratios is represented obvious and logically consecutive. Visually are established on what independent variables they depend, you watch the equations (5), (9), (12). Formulas for final (integrated) expressions (4), (8), (13) follow from the equations for full differentials.

We will consider some results of a conclusion of the same equations on the basis of integrated consideration, so-called integrated approach now, using results of works [8-12].

At the same time at the beginning some G, F, H functions which are presented by the integrated equations (4), (8), (13) – [8-12] are just entered into consideration. Then the full differentials of these functions expressed by formulas (2), (3), (5) – (7) are calculated, (10) – (12).

Further, using the received systems of the equations in a differential form, we come to equality (1).

It is possible to call this way of the proof “reverse motion”. Going from some integrated formulas (13), (8), (4), we come to the equation (1) [8-12]. Arrival to a formula (1) serves as the proof of correctness of integrated formulas. At the seeming evidence and simplicity, this way of the proof of a correctness of formulas (4), (8), (13) possesses that shortcoming what doesn’t answer a question and from where have undertaken, initially from where integrated formulas (4), (8) and (13) have appeared?

There is the following question. What will be (what will change) if we consider the forward stroke of the proof given above on the basis of integration of the differential equations (1), (5), (9), (12) for final process between points 1 and 2, you watch figures 1 and 2?

In figure 1 thermodynamic process in P-V coordinates from works is shown [8-12]. The proof is carried out on the basis of consideration of thermodynamic work in two of her versions: PdV and VdP for process between two points 1-2 [8-12]. Thus, on the basis of the analysis of the schedule of thermodynamic process the following formula [8-12] is proved

01,2 = ^ 2    ^ i    ^ 1,2 ,                                                   ⁽ 14)

where W_V1 = ^ VdP - work against pressure forces.

Formula (14) we call integrated because final expression for H (formula 4) turns out at integration н of dQ (1) under zero entry conditions. Also final differential expression jH dH = H — Ho, turns out, you watch a formula (4).

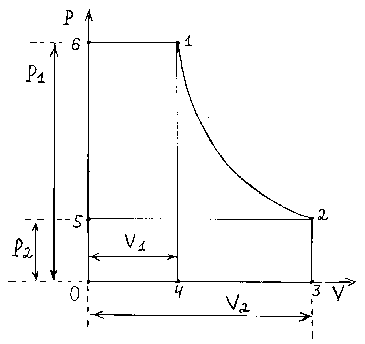
Fig. 1. Scheme of Thermodynamic Process in P-V coordinates [8-12].

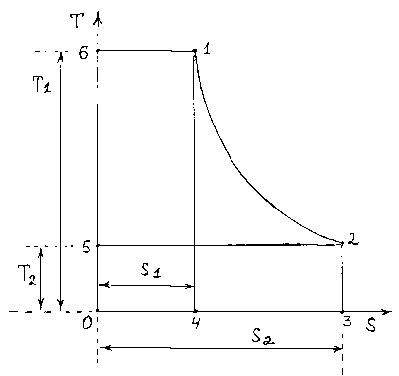
Fig. 2. The scheme of thermodynamic process in T-S coordinates

From (14) the proof of an integrated formula (4) also follows.

Now, following the logic of calculations used in works [8-12], we will carry out a conclusion of the main integrated equations (4), (8), (13). Our difference is expressed only that we in addition use the schedule of any thermodynamic process in T-S coordinates. Change of thermodynamic functions in the intervals final (limited), fixed, between points 1-2 is considered.

In figure 2 the schedule of any thermodynamic process in T – S coordinates is shown.

From consideration of this drawing it is visible that

5 1,2, 3 ,4 + 5 б,_1Л0 - 5 о,₅, 2 ,3 = 5 б,1,2, ₅ ,                                               ⁽¹⁵⁾

where 5 ij, _kil - the area of a figure limited to points of i,j, k,l .

On the basis of (15) we will receive that

£ TdS + ТД - T2S2 = - J12 SdT.                               (16)

Further on the basis of (14 ) and (15) we will rece i ve

.

j; TdS = T2S2 - ТД - j SdT = H2-H1-j1 VdP

Integrated formulas (8) and (13) directly follow from a formula (17).

At the same time used the graphic analysis of thermodynamic process in T-S and P-V coordinates in common.

Thus we have proved that the basic thermodynamic formulas for Gibbs’s function – G, Helmholtz – F and enthalpies – H it is possible to bring out of integrated consideration of thermodynamic process correctly. When all changes of the main sizes happen in final (limited, fixed) limits, points 1-2 in figure 2. From the integrated equation (17) it is also visible that variables for the G-(13) function are P and T. Therefore, integrated consideration leads without any complications to the same obvious results, as differential consideration. At the same time, the initial, starting moment is the physical law of conservation and transformation of energy expressed in thermodynamic sizes – (1).

By consideration of mechanical work which is spent for change of volume of gas the formula [813] is used

S^Fds = £ k dV where F-force, N, the s-passmble way, m, P-pressure, Pa, V-the volume, m3.

From the point of view of mech a nics force is function from the passable way of F=F (s). From

• - 2

this it follows that the following function J_v F(s')ds is integrated. It is standard. However, in

k mechanics it isn’t accepted to integrate as work expression Ja s(F)dF. Though, from the point of view of mathematics the F(s) function can always have an inverse function of $(F). Therefore, by consideration of some physical processes function and an independent variable (argument) aren’t rearranged by places at integration. The thermodynamics shows us that such shift by places when the argument turns into function, and function plays an argument role (an independent variable)

it makes a certain physical sense. As an important example we will give definition of entropy of

Д5 > f^-^ (see formula (16)) where the absolute temperature of T in this case plays a role of the integrated T=T (Q) function, the expression standing under integral, and an independent variable is the amount of heat of Q.

In this regard we had had some new, additional views on interpretation of two types of thermodynamic work of PdV, VdP and their communication with other members in the general law of energy conservation. In work [11] (paragraph 2-1) the following equations which express the first law of thermodynamics and the law of energy conservation in moving volume are presented, you look also

[5-7]:

AQ = AU + P₂V₂ - P^ + M^^ + Mg (h₂ - h_T) + L_tech ,         (18)

дQ _д^ । у PdV                                                (19)

where AQ - warmth, J, M - the mass of gas, kg, g - the acceleration of gravity, m /s2, h-height showing change of potential energy, m, w1, w2 – stream speeds in two various sections, m/s, Ltech – technical work, J.

•                                                                          fthl

On the basis of comparison of two various records (types) of the law of energy conservation (the law of thermodynamics) in [5-9, 11, 12] for specific work of expansion of gas the following equation is received l = ^pdv = p2U2 - p1V1 + --.,;,    ,.). ltech.                  (20)

In the equation (20) all members are carried to unit of mass, l_tech =[J/kg], v=[m³/kg], l = [J/kg]. P i                                                  J

However, at a conclusion of the equation (20) in certain cases can make a mechanical mistake. In

/ our opin ion, the first law of thermodynamics in her expanded record, or in other words, the law of energy conservation in the moving volume of a gas stream taking into account different types of transformation and change of energy, if is neoessarу or write down in the form of (18) or in the follo wing look

Wz dq = du+- d(pv) + d — + gdh + dlteck.

At the same time it is necessar y to consider that expansion work J pdv already contains it (is included) in gas l pushing through work l p^ , dq = [J/kg].

Presence of the following two members

% ! = JpWv,

- 2 = (^ 2 — P 1 ^ 1 )

in the right part of these equations means that they also, as well as other functions x3 = Au , x , 2 x^g^-hi), -I , x6 = ^tech.

are equivalent and absolutely independent variables for function

AO = f(x₁,x₂,x₃,-,x_n⁾ .

At the same time we assume that there are unambiguous (continuous) inverse functions

Xi = Vi(Aq,Xj).

At the same time, from the point of view of physics of process of X j ^ x_t . Therefore, formulas (18), (21) are true. Our these representations are confirmed also by results of work [14]. Therefore, the equations (18), (21) are only expanded option of a formula (1) where possible types of change of energy of a stream of the gas moving in a potential gravitational field and other possible types of technical work are in addition considered. In other words, without formulas (18) and (21), the size x 1 and x 2 – formulas (20), (22) – (24) can’t be connected directly among themselves in any way.

Existence of some physical law, (18), (19), (21) doesn’t mean similar at all that between h is independent variables surely there has to be some direct functional link of x_i = e^ / i. In which there is no binding member A q , watch a formula (20).

It should be noted that work of pushing through of l_p ^ = XP i ^v i - Р г ^у г ) doesn’t appear

«automatically» when replacing the variable x₁ on «^ = x₂ — J^P2 vdp, you watch formulas (19) - (23) as it can seem in certain cases.                                 " '

The matter is that work of pushing through of l_p,v is absolutely independent variable in the general expression (18). Work of pressure at pushing through of liquid volume can be performed by external foreign forces.

Formulas (18), (21) can also be brought out of the general law of energy conservation in the moving final volume of liquid or gas [15 – a formula (11)], [16]. For this case we will formulate the law of energy conservation in the form of the following integrated ratio, fair for the mobile final volume of the continuous environment

(    2^)

T- Jp ei + wr + epot,g d6 = Jpfm •wd6 + ifpn •wd^ + dT V (     2        J VF

Jqf • nda + Jqmpd6 + JqRpd6 + J^pd6, FV  VV

Where e_i – internal energy per unit mas s, J/kg, e_pot,g – the potential energy of unit of mass of liquid connected with leveling height, J/kg, w – the speed of the movement of liquid or gas, m/s, q _f – a thermal flow of Fourier, W/m², q_R – a thermal stream from radiation, W/kg, q_m – a thermal stream from mass sources of heat, W/kg, p_n – a vector of density of superficial force, Pa, f m – the mass density of volume force, N/kg, l^m_tech – all types of technical work carried to unit of mass and to a unit of time, W/kg.

Carrying out some transformations and calculations similar to that which are carried out in work [15], we have proved that from an integrated formula (26) the equations for final thermodynamic process (18), (21) turn out. The formula (26) differs from a formula (11) from work to [15] those that at the right part there is an additional member for technical work l™h, J/kg.

Using a formula for differentiation of the integral taken on mobile volume we will receive [15]

and

d

J p dTv

Г    w 2        )

ei ■ 2 ■ epot,g de = J к 2        J V

J

V

We will consider th at

■

div w -p

к

/

/

■

div w -p

■

d

dt

w2

^ei ⁺T^{+ e}Pot,g

к

/

p

- 2

w ei + 2 + epot,g

d e .

w 2

e i ^{+     +} e pot,g

к

^

J J

/

w - div p

-2

w

e; +    + e i2

pot,g

/

(

+p

—■ 2

e i ⁺ w" ^{+ e} pot,g

к

к

J J

к

L

9т

- 2 w

^p e i ⁺ 2 ^{+ e}pot,g

к к

h

+ w ■ div

(

P

к

)

J J

de+

) div ( w ) ,

J

I "*2 w ei + "y + epot,g

к

^

) )

d dT

P

I -2       )

w e+T+ePot,g

к               )

full derivative of a total energy of some final volume of the moving environment.

Substituting (27) - (29) in (26), we will receive the equation

1 f

V^{d T}

P

^    w2

e i ⁺ -2- ⁺ e pot,g v

) 1

d0 =

v

j pfm • wde

V

+ J div ( Pn • w ) de +

+ J ^d ivq f^{d e} + J Q m^{d e} + J q R^{d e} + J ^ch pde ^- J V   VVV   V

(   ^{— 2} ^

w pei+v v v

div ( w ) de,

where

Pxx Pyx Pzx Pxy pyy pzy (Pxz Pyz Pzz J tensor of superficial pressure forces, n – a single normal to a surface of the considered volume.

As integration volume same for all members, all integrals it is possible to unite in one general integral. Rejecting integral, leaving only under integrated expression, from (30) it is possible to receive d dt

(

Pe i v

—2

w

⁺ 2 ⁺ e ^pot,^g

——           • pfm • w +

div ( Pn • w )

+

(    "— 2          ^

divqf+Q m + Q R - P

div ( w ) .

e i ⁺T⁺ >t,g

V                7

Thus, emergence of two members of the equations follows from property of mobility (expansion or compression) borders of the considered volume: 1-convective part for a full derivative w • div p

V

(      "— 2

w ei + 2 + epot,g

V

)

2 – a possibility of change of a total energy of individual volume of liquid as a result of volume deformation (compression or expansion) with an invariable weight in total amount

p

-2 w ei +2 + epot,g

d iv ( w ) . ^V

^We will accept that volume forces and thermal streams qi are absent, liquid div f w ) =0 aren’t squeezed. Also liquid doesn’t proceed outside and doesn’t flow in i ns id e into this considered volume.

Under these c ndi ion i i possible t int grate (30 , presenting her in the form f d

w 2

^p e i ⁺ "У ^{+ e}pot,g

'l l 2

I = !^{[ d,v ( Pn} ^ ^w »t.

The analysis shows th t the e uatio (34) can e integrated, accepting an assumption that liquid ideal which has no tangent ten ion, exis s onl th ydrostatic pressure of p ij = – p δ ij . In case of the onedimensional movement fro (34) have r eived the following equation

/    2 \

A ( pe , ) + A pw x +A ( pe pot,g ) = ^A p +fpiw x idw x .

2      , V jw

V V                            1

V

V

here at e h member the sign means change i a final interval, for example Δp = p2–p1. The fact that (35) expresses the law оf energy conservation is confirmed by the following check according to the theory of dimension [p] =

N • ^ J

—----= — also expresses the work made in unit of volume at rnt •m m3

change of pressure upon final size. The right part of a formula (35) shows that generally the work

- performed by pressure forces consists of two parts: 1 work connected with change of pressure – VdP,

• 2 – the work connected with change of volume – PdV. Such “variety”, increase in a type of work for superficial pressure is connected with transition from superficial integral to volume for expression in formulas (26), (30), (34) according to Ostrogradsky-Gauss’s theorem. In other words, integrated consideration contains (includes) all possible types of works which are connected with changes of volume and pressure of gas. In this sense integrated consideration is “slightly richer”, than differential consideration of thermodynamic process.

Thus, differential ratios and vice versa follow from the integrated description, these two methods of the description are absolutely equivalent with each other on the end result for thermodynamic sizes.

In work [15] it is proved that formulas (members) (32) and (33) turn out not only as a result of expansion of volume border. Leads to the same formulas also presence of a convective stream of weight and energy through the closed fixed surface which limits the set elementary volume of the j t = J c Whhc , where h - an enthalpy. We will consider a well-known formula for full, substantiate derivative some physical quantity φ – [17]

-^^(t,%(t),y(t),z(t)) = ^ + u^ + v^ + w^_                  (36)

dt                          at dx dy 9z

Results [15] and formula (32) show that the convective component in (36) can result: 1 changes of volume, expansion or compression of border of volume (by integrated consideration), 2 flowing or an effluence of a stream of mass of substance which it is connected are transferred with itself by a stream of this scalar jt = ^ p w^da . By differential consideration when volume is considered elementary and his external borders aren’t mobile.

Conclusions

• 1.    Use of the rule of replacement of variables of integration leads to correct conclusion of the main thermodynamic functions (an enthalpy, Helmholtz’s function and Gibbs’s function) by integrated consideration of thermodynamic process in final intervals of change of parameters.

• 2.    Integrated consideration of the law of energy conservation in a general view for moving final volume of liquid or gas leads to «expanded» option of formula for the first law of thermodynamics written down in differential form taking into account different types of technical and thermodynamic work.