ACO Algorithm Applied to Multi-Objectives Optimization of Capacity Expansion in Next Generation Wireless Network

Published Online September 2013 in MECS

Available online at

The Next Generation Wireless Networks (NGWNs) are expected to provide high data rate and optimized quality of service to multimedia and real-time applications over the Internet Protocol (IP) networks to anybody, anywhere, and anytime. The wireless network infrastructure consists of equipment required by mobile network operators to enable mobile telephony calls or to connect fix subscribers by radio technology. The interacting layers architecture of next generation wireless network is shown in fig.1.

* Corresponding author.

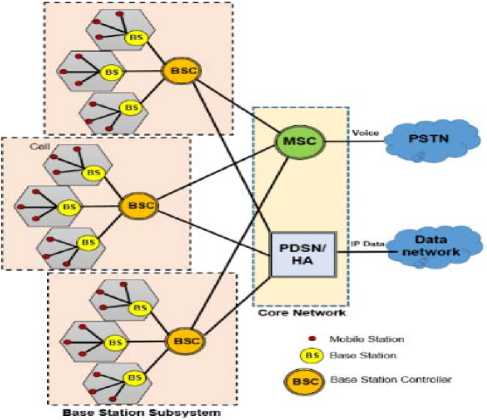
Fig. 1. The next generation wireless network infrastructure

The architectural building blocks enabling mobile telephony are:

• i)    The core network : comprised of the mobile switching centers (MSC), the packet data serving nodes (PDSN), and home agents (HA), and

• ii)    The base station subsystem (BSS) also known as the radio access network, consisting of base station controllers (BSC), base transceiver stations (BS), and mobile stations (MS).

• 2.    Problem formulation

Each BS is typically assigned a group of radio channels to support a number of mobile stations in its cell. BS’s at adjacent cells are assigned different sets of frequencies. The antennas of a BS are designed to achieve coverage only within the particular cell. By limiting coverage of a BS to its cell area, the set of frequencies assigned to this BS can be reused at other BS’s that are distant enough to keep co-channel interference within acceptable limits. The MSC is a modified central office switch, with extensions for mobile subscriber databases and intelligent network links, which enable the MSC to decide where to route an incoming call. If the requested subscriber for example is registered to be located in the MSCs area, the call will be routed to the respective BSC. The BSC is part of the link between the BS and the MSC and is responsible for allocating and releasing radio channels to the MSs by way of the BS. In addition to managing channels on a radio interface, the BSC is also responsible for managing MS handovers to other radio channels. Other BSC functions include routing calls to the MSC, handling call control processes, and maintaining a database of subscribers and records of calls for billing [2]. The BSC is directly connected to the MSC and the PDSN. The PDSN is the point of entry into the wireless packet data network for mobile subscribers. The PDSN performs two basic functions [1], which are (1) exchanging packets with the mobile station over the radio network and (2) exchanging packets with other IP networks. The PDSN is generally coupled with HA, which is a router on a mobile node's home network that maintains information about the device's current location, as identified in its care-of address [3]. Corresponding to the architectural building blocks of a wireless network, are three types of interconnects [4]. These are (1) mobile device to BS interconnect, which includes both forward and reverse radio links, (2) the BS to BSC interconnect, which is called the backhaul, and (3) BSC to MSC interconnect.

In the network design and capacity planning literature, conventional approaches to meeting demand growth include location and installation of additional network elements [5-6]. The more commonly known hierarchical capacitated concentrator location problem, which is an extension of the concentrator location problem to multiple levels and a classical research issue in the telecommunications literature [7-10]. However, this approach ignores two important aspects of upgrading to NGWN. The first importance of backward compatibility with pre-existing networks, and the second is the cost and operational benefit of gradually enhancing networks, by replacing, upgrading and installing new wireless network infrastructure elements that can accommodate both voice and data demand. In [6], the author used a greedy heuristic algorithm to solve the maximal coverage location problem in cellular communication Systems. A Tabu search algorithm and genetic algorithm approach to cellular capacity expansion to maximizing the coverage area and minimizing the number of transmitters is presented in [11-12]. Yu et al in [13] proposed a set covering algorithm for given traffic and finding optimal solution configuration in a CDMA network. A greedy strategy to optimal positioning of base stations for cellular radio networks and capacity planning of UMTS networks studied in [14-15]. An alternate approach to capacity planning and expansion is introduced for 3G network system capacity without an increase in base stations using a cell splitting approach [16]. In [17], the authors studied the base station location and service assignment problem in a W-CDMA.

The recently research in [18-22], we have proposed a novel particle swarm optimization (PSO) and ant colony optimization (ACO) algorithms to optimal location of controllers in wireless networks and centralized wireless access network. In this paper, we focus on the Multi-Objectives Optimal of Capacity Expansion (MOOCE) in NGWN and propose a novel ACO algorithm to solve it. The rest of this paper is organized as follows: Section 2 presents the MOOCE problem formulation. Section 3 presents our new algorithm to solve it based on ACO algorithm. Section 4 presents our simulation and analysis results, and finally, section 5 concludes the paper.

In this section, we assume the network topology of base station subsystems havem mobile users, n base stations, and p base station controllers. We introduce the following notation:

Table 1. Notation defininition.

Notation	Meaning
M	Index set of Mobile user locations: M = { MS i , V i = 1.. m }
N	Index set of all Base Station (BS): N = N 1 U N 2 = { BS j , V j = 1.. и } N 1: Index set of existing BS; N 2: Index set of potential BS
P	Index set of Base Station Controllers (BSC): P = P 1 и P 2 = { BSC k , V k = 1.. p }
T j	P 1: Index set of existing BSC; P 2: Index set of potential BSC Set of types available for BS j , V j' G N
S	[ 1 if commondity type is voice Set of commodity types: 5 = < [ 2 if commondity typeisdata
Nt	Index set of all BS of type t. N t = N 1 t и N 2 t
Di s	Demand of commodity type 5 for mobile user MS i , V i G M
MaxBS _ Capj MaxBSC _ Capk d ij t	Maximum capacity of BS j type t , V j G N t . Maximum capacity of BSC k , V k G P Distance of mobile user MS i from BS j of type t V i G M , V j G Nt

Notation	Meaning
MaxBS Cov jt cost connect jtk cost_install k cost_upgrade j cost_setup j	M aximum coverage range for BSj of type t Cost of connecting BSj of type t to BSCk Cost of installing BSC k , V k e P 2 Per channel cost of upgrading BS j , V j e N 1 Cost of constructing and connecting BS j , V j' e N 2

The MOOCE in NGWN problem has two steps the initial assignment of MSs to BS and the connection of BS to BSC and capacity expansion and traffic increase with constraint specifies that:

• •    Each mobile user MS i will be assigned to exactly one base station BS j of type t

• •    Mobile usersare within that base stations’ maximum range MaxBS Cov

• •    At most one base station of type t can exist at location j

• •   if a base station BS j is operated, it has to be connected to a BSC k and the BSC has to be active.

• •    The capacity constraints of the model, in which we argue that BSs must have the necessary

capacity to accommodate traffic demand of all demand types s for all MSs assigned to it and the BSC must have the necessary capacity to accommodate all BSs assigned to it.

In the first step, we use the indicator variables are:

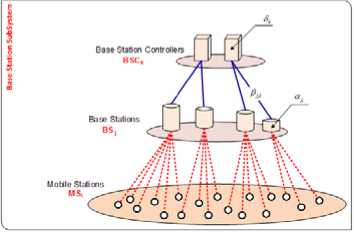
Fig. 2. The Initial Assignment step with indicator variables

“j.

P jk

5 k =

1 if BS_j of type t is operated 0 otherwise

1 if BS _j of type t is connected to BSC_k 0 otherwise

1 if BSC_k is operated in initial assigment 0 otherwise

Fig.2 show an example of an existing initial assignment that each mobile user can be assigned to only one BS, while each BS has to be connected to a single BSC.

In the second step, we use the decision variables are:

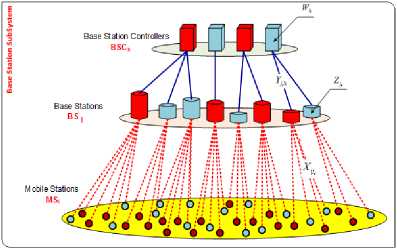
X ij t

Y j t k

f 1 if mobile user MSi is connected to BSj [0 otherwise f 1 if BSj of type t is connected to BSCk

10 otherwise fl if BSj of type t is operated j [0 otherwise f1 if BSCk is operated k 10 otherwise

Fig. 3. The assignment after capacity expansion and traffic increase with decision variables

Fig.3 illustrates an assignment after capacity expansion and traffic increase, and indicates the respective decision variables. New wireless BSS infrastructure equipment with BS and BSC in red shades. The objective of MOOCE is to minimize the total cost of expanding an initial wireless BSS to accommodate increased traffic demand. The MOOCE problem can be defined as follows:

^Min Z Z Z c^ost_connect _Jtk ( j - P j^ ) + Z ^cost_intall k ( W k - § k )

j =1 k =1 t eT ,                                                  k e P₂

(_

+ Z cost_upgrade _j Z MaxBS _ cap, ( Z, - a _jt ) + ZZ c ost_setup _j Z_j j e N ₁                        I t e T                                       J j e N ₂ teT ,

Subject to:

n

ZZXu. =1 Vi=1--m j=1 t eTj d-.X,, < MaxCov. Z,, Vi = 1..m, j = 1..n, t e T ij ijt                                jtjt                                                                  j

ZZj, < 1, Vj = vn t eTj

p

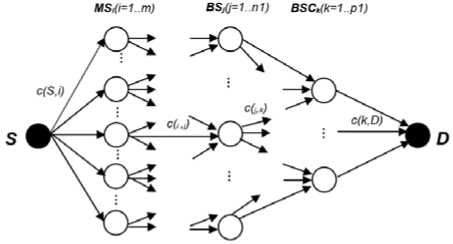
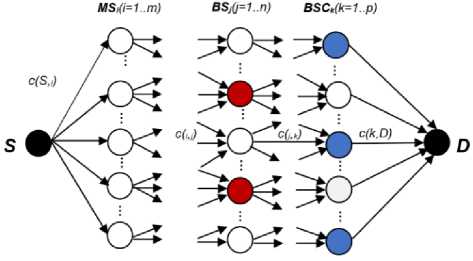
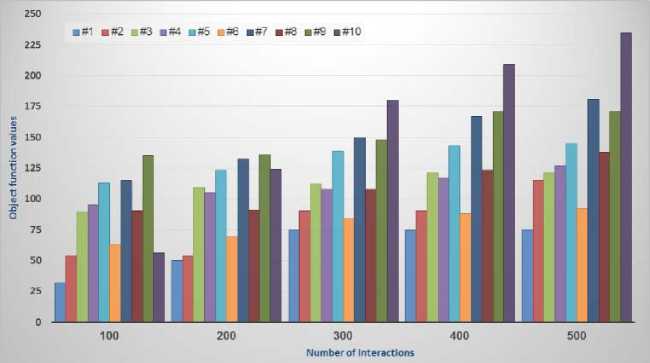
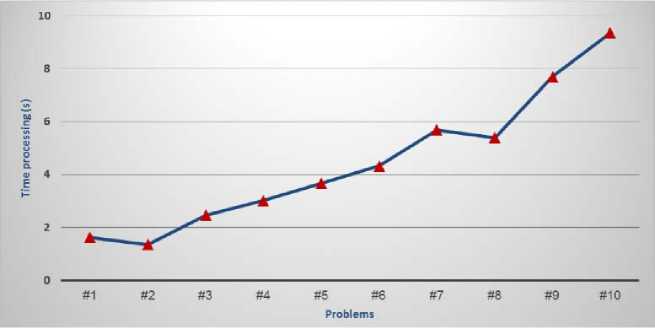
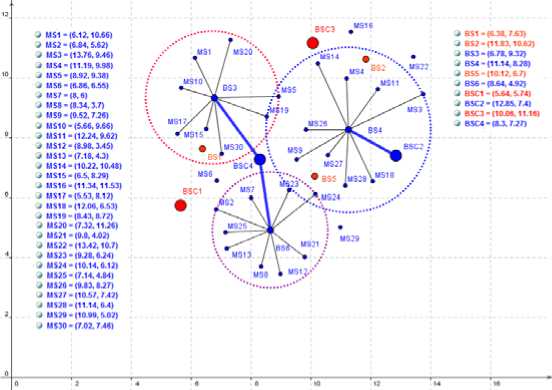
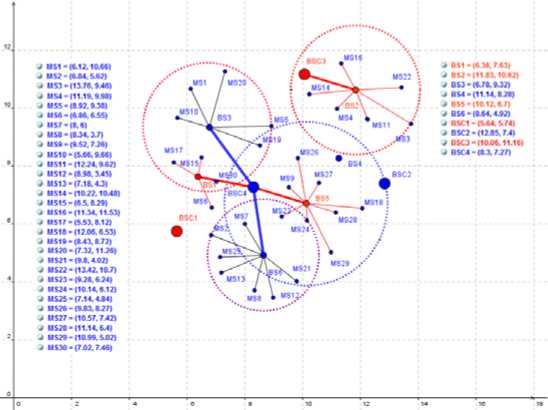
Zj.

Yjk< W_fc, Vk = 1..p, j = 1..n, t e Tj                                                                             (6)

m2

ZZD'sX.,< MaxBS_Cap, xZ,, Vj = 1..n, t e T

E E Yjk - MaxBSC _ Capk^xWk, V k = 1.. P j=1 ‘ eT '

Xj, e {0,1}, j e {0,1}, Zj, e {0,1}, Wk e {0,1}

V i = 1.. m, j = 1.. n, k = 1.. p, t e Tj

• 3.    ACO based Algorithm for The MOOCE

  • 3.1.    Ant Colony Optimization

• 3.2.    Solving the MOOCE based on ACO

The ACO algorithm is originated from ant behavior in the food searching. When an ant travels through paths, from nest food location, it drops pheromone. According to the pheromone concentration the other ants choose appropriate path. The paths with the greatest pheromone concentration are the shortest ways to the food. The optimization algorithm can be developed from such ant behavior. The first ACO algorithm was the Ant System [23], and after then, other implementations of the algorith m have been developed [24].

In this section, we present application of ACO technique with the dynamic local heuristic information for the MOOCE problem. Our new algorithm is described as follows:

In the first step, we construct a transportnetwork G1 = (V1, E1) , where V1 = M О N1О P1 in which M = {1,2,..., m} is the set ofMSs, N1 = {1,2,..., n1} is the set of existing BSs, P1 = {1,2,..., p1} is the set of existing BSCs and E1 is the set of edge connections between MSi toexisting BSjand existing BSjto existing BSCk satisfy constraints. We find the maximum flowof the transport networkG1 by adding two vertices S (Source) and D (Destination) is shown in Fig.4 to defines indicator variables.

Fig. 4. The Initial Graph G1 determine the indicator variables

In Fig.4, nodes has white color isset of existingMS, BS, BSC. The weight of the edges on the graph G1is defined as follows:

• •    The edges from vertex S to MSi is demand of commodity type 5 for mobile user, denoted as

c(S,MSi)= D_i^s , (i=1..m).

• •    The edges from MSito BSj is capacity of MSi if MSi is connected to BSj,denoted as c(i,j)= D^ss , (i=1..m, j=1..n1).

• •    The edges fromBSj to BSCk is total capacity of MSi is connected to BSj,denoted as

c (j, k )=    Z D, (j = 1. n1, k = 1.. ^1)                                                             ⁽¹⁰⁾

MSiconnectedBSj

• •    The edges fromBSCkto vertex D is total capacity of BSj connected to BSCk,denoted as

c(k,D)=     Z     c(i,j), (j = 1..n1, k = 1..p1).                                                       ⁽¹¹⁾

BS jconnected BSCk

In the second step, we construct a transportnetwork G2 = (V2, E2) , where V2 = M U N U P in which M = {1,2,...,m} is the set ofMSs, N = {1,2,...,n} is the set ofBSs, P = {1,2,...,p} is the set ofBSCs and E2 is the set of all edge connections between MSi toBSjand BSjto BSCk_.

Fig. 5. The FullGraph G2 determine the decision variables

Fig.5 show all edge connections possible satisfy the constraints (2)-(9). In which, red nodes areset of potential BSs, and blue nodes are set of potential BSCs.

1 if i e [1..m] then MSi is operated

Xi ='

if! e [ m +1.. m + n ] then BSj is operated (j = i - m)

if! e [ m + n +1.. m + n + p ] then BSC_k is operated (k = i - m - n)

0 otherwise

In our case, we use real encoding to express an element of the pheromone matrix is generated by graph G2 that represent a location for ant movement, and in the same time it is possible receiver location. A path by each Anti, pheromone intensities on links are evaporated with a pheromone update rule. Each edge (i, j)of the graph G2 is associated a total pheromone concentration Ti, . At each node, each Antkexecutes a decision policy to determine the next node of the path. If Ant_kis currently located at node i and it selects the next node j e Ni according to the transition probability defined by:

^k pij

[t, ]* П ]"

ST ]* [j l e Ni where, Tij is the pheromone content of the path from node i to node j, Nk is the neighborhood includes only locations that have not been visited by ant k when it is at node i, ηijis the desirability of node j, and it is a problem-dependent function to be minimized given by:

n,

1 d_ij

where d_ij is the cost of connect from MS_i to BS_j or BS_i to BSC_j .

The influence of the pheromone concentration to the probability value is presented by the constant α, while constant β do the same for the desirability. The ants deposit pheromone on the locations they visited according to the relation.

new current

T = Tj

+ ^TkJ

where At* is the amount of pheromone that Anti exudes to the node j when it is going from node i to node j.

This additional amount of pheromone is defined by:

^Ti

(cost_connect, + cost_intall j + cost_upgrade j + cost_setup j)

The cost functionfor the Antkby the formula (1). This algorithm will terminate either when the maximum number of iterations is reached or an acceptable solution is found.

• 3.3.    Our Algorithm

The pseudo-code of ACO algorith m to solving MOOCEas follows:

ACO ALGORITHM

INITIALIZATION:

Algorithmparameters: a,в

Antpopulationsize: K.

Maximumnumberofiteration:N_Max.

GENERATION:

Generating the pheromonematrixfor the Ant_k.

Update the pheromonevaluesandset x*=k;

i=1.

REPEAT

FORk = 1 TOKDO

Computing the costfunctionfor the antkby the formula (1)

Computingprobabilitymoveofantindividualby the formula (13)

IFf(k) <f(x*)THEN

Update the pheromonevaluesby the formula (15) Setx*=k.

ENDIF

ENDFOR

UNTILi>NMax

• 4.    Experiments and Results

  • 4.1.    The problems tackled

• 4.2.    Parameters for the ACO algorithm

• 4.3.    Numerical Analysis

In our experiments, we have tackled several MOOCEinstances of different difficulty levels. There are 10 MOOCEinstances with values for M, N and P shown in Table 2.

Table 2. Main characteristic of the problems tackled.

1 Рк*лА 1тм	Mobile Users	Base Stations				Base Stations Controllers
ro em        (M)		N	N1	N2	Types	P	P1	P2	Types
1.	10	4	3	1	1	3	2	1	1
2.	20	5	3	2	2	4	3	1	2
3.	30	6	3	3	3	4	2	2	3
4.	40	7	3	4	3	5	2	3	3
5.	50	10	6	4	3	5	2	3	3
6.	60	15	10	5	4	10	5	5	4
7.	70	15	8	7	4	10	6	4	4
8.	80	20	10	10	5	15	10	5	5
9.	90	25	15	10	7	15	8	7	6
10.	150	40	20	20	10	20	10	10	7

We have already defined parameters for the ACO algorithm shown in Table 3:

Table 3. TheACO Algorithm Specifications

Ant Population size	K = 100
Maximum number of interaction	NMax = 500
Parameter	а=1, в=10

We evaluate the performance of our algorithms to optimize of capacity expansionwith multi-objectives. The experiment was conducted on Genuine Intel® CPU DuoCore 3.0 GHz, 2 GB of RAM machine. We ran experiment ACO algorithm implemented using C language. The experimental results of our algorithm shown in Fig.6 and Fig.7.

Fig.7. Time processing MOOCEinstances tackle

The results show that problems with the small number of M, N, P such as problem #1, #2, #3, #4 and #5, algorithm has approximate optimal results fast with small interactions.However, when the problem size is large, the optimal results may be slower such as problem #6, #7, #8, #9 and # 10.Convergence speed is not the same and depend on the distribution of parameters data.

Fig.8 show an existing init ial assignment of problem #4. In which, BSC2, BSC4 are existing BSCs; BSC1, BSC3 are potential BSCs; BS3, BS4, BS6 areexisting BSs; BS1, BS2, BS5 arepotential BSs. MS6, MS29,

MS16, MS22 are not connected. Fig.9 show an optimal solution with BSC2 is replaced by BSC3, BS4 is replaced by BS2 and BS5. BS1 is added and connect to BSC4. Red edges are replace connections.

Fig.8. An existing initial assignment of problem #4

Fig.9. An optimal capacity expansion of problem #4

From this result, we confirmed that this isa promising approach to solve this problem.

• 5.    Conclusions

In this paper, we propose a novel ant colony optimization algorithm to solve a network topology has two levels in which mobile users are sources and both base stations and base station controllers are concentrators.

Our objective function is the sources to concentrators connectivity costas well as the cost of the installation, connection, replacement, and capacity upgrade of infrastructure equipment. Our experiment results show that our algorithms is a promising approach to solve this problem.

• [1] . Commworks, Wireless Data for Everyone. http://www.commworks.com. Technical Paper, 3Com Corporation, 2001.

• [2] . Fente, F.J. et al.. Planning of the base station interconnection network. Comunicaciones de Telefónica I+D, Issue 15, 1997.

• [3] . IETF RFC. IP Mobility Support, 2002.

• [4] . Siemens Mobile. UMTS. http://www.siemens.de. White Paper, 2001.

• [5] . Balakrishnan, A., Magnanti, T., Shulman, A. and Wong R, Models for Planning Capacity Expansion in Local Access Telecommunication Networks. Annals of Operations Research, No. 33, pp. 239-284, 1991.

• [6] . Tutschku, K. Demand-based radio network planning of cellular communication Systems. In Proceedings of IEEE Infocom’98, pp. 1054-1061, 1998.

• [7] . Mirzaian, A. and K. Steiglitz. A Note on the Complexity of the Star-Star Concentrator Problem. IEEE Transactions On Communications. No. 29, pp.1549-1552, 1981.

• [8] . Gavish, B. A System for Routing and Capacity Assignment in Computer Communication Networks. IEEE Transactions of Communications, No. 37, pp. 360-366, 1989.

• [9] . Narasimhan, S. and H. Pirkul. The Hierarchical Concentrator Location Problem. Computer Communications, Vol. 15, no. 3, pp. 185-191, 1992.

• [10] . Gupta, R. and J. Kalvenes. Hierarchical Cellular Network Design with Channel Allocation. In Proceedings of the Ninth Annual Workshop on Information Technologies & Systems. pp. 155-160, 1999.

• [11] . Lee, C.Y. and H. Kang. Cell Planning with Capacity Expansion in Mobile Communications: A Tabu Search Approach. IEEE Transactions on Vehicular Technology. Vol. 49, No. 5. pp. 1678-1691, 2000.

• [12] . Calegari, P., Guidee, F., Kuonen, P. and Wagner, D. Genetic approach to radio network optimization for mobile systems. IEEE VTC, pp. 755-759, 1997.

• [13] . Yu, C., S. Subramanian, and N. Jain. CDMA cell site optimization using a set covering algorithm. In Proceedings of Eight Int. Network Planning Symposium, pp. 75-78, 1998.

• [14] . Mathar R. and T. Niessen. Optimum positioning of base stations for cellular radio networks. Wireless Networks. Vol.6, No.6. pp. 421-428, 2000.

• [15] . Mathar R. and M. Schmeink. Capacity Planning of UMTS Networks. In Proceedings of Sixth INFORMS Telecommunications Conference, Boca Raton, Florida 2002.

• [16] . Giuliano, R., F. Mazzenga, and F. Vatalaro. Smart cell sectorization for third generation CDMA systems. Wireless Communications and Mobile Computing. Vol. 2, Issue 3, pp. 253-267, 2002.

• [17] . Kalvenes, J., J. Kennington and E. Olinick. Base Station Location and Service Assignment in W-CDMA Networks. Technical Report 02-EMS-03. SMU, 2002.

• [18] . Dac-Nhuong Le, Nhu Gia Nguyen, and Vinh Trong Le, A Novel PSO-Based Algorithm for the Optimal Location of Controllers in Wireless Networks, International Journal of Computer Science and Network Security (IJCSNS), Vol.12 No.08, pp.23-27, 2012.

• [19] . Dac-Nhuong Le, PSO and ACO Algorithms Applied to Optimizing Location of Controllers in Wireless Networks, International Journal of Computer Science and Telecommunications (IJCST), Vol.3, No.10, pp.1-7, 2012.

• [20] . Dac-Nhuong Le, PSO and ACO Algorithms Applied to optimal Resource Allocation to Support QoS Requirements in Next Generation Networks, International Journal of Information & Network Security (IJINS) , Vol.2, No.3, pp.216-228, 2013.

• [21] . Dac-Nhuong Le, Optimizing the cMTS to Improve Quality of Service in Next Generation Networks based on ACO Algorithm, International Journal of Computer Network and Information Security(IJCNIS), Vol.5, No.4, pp.25-30, 2013.

• [22] . Dac-Nhuong Le, Nhu Gia Nguyen, and Vinh Trong Le, A Novel Ant Colony Optimization-based Algorithm for the Optimal Centralized Wireless Access Network, in Proceeding of Third International Conference on Computer Science, Engineering &Applications ( ICCSEA-2013), Springer 2013.

• [23] . M. Dorigo, V. Maniezzo, and A. Colorni, Ant system: Optimization by a colony of cooperating agents, IEEE Trans. on System, MAN, and Cybernetics-Part B, vol. 26, pp.29-41, February 1996

• [24] . M. Dorigo, M. Birattari, and T. Stitzle, Ant Colony Optimization: Artificial Ants as a Computational Intelligence Technique, IEEE computational intelligence magazine, November, 2006.