Acoustic waves propagation in heated water with vapor bubbles

It is known that a bubble liquid is a system with unique wave properties [1,2]. Problems of the wave propagation in such media have been of great interest to researchers for almost half a century due to the wide spread of this systems in nature and their intensive use in modern technology.

The papers [3–6] consider a stationary flow of a bubble gas-liquid mixture in a nozzle of circular cross-section and analyze the possibility of realizing of superhigh temperatures and pressures in the gas phase at the nozzle section near the minimum cross section. Also, the papers study the effect of the parameters (the initial radius and the volume content of bubbles determining the composition of the volume flow of liquid fed into the nozzle) on the flow pattern.

The papers [7–10] present the developed models of a gas-liquid mixture for investigating low-amplitude pressure waves in bubble media. The case of strong shock waves is considered in [11–13]. In the two-dimensional formulation for low-intensity pressure waves, the criteria for quenching and amplifying the wave signal in bubble regions of finite dimensions [7, 9, 10] are determined. It is established that in the evolution of a pulsed signal in a homogeneous bubble liquid, a leading wave and a divergent wave packet [8] can form in the transverse coordinate of the pulse signal. For a reliable description of the thermodynamic properties of bubble liquids under conditions of strong shock waves, a wide-range equation of state of water and vapor was used in analytical form. Calculations were compared with the experiments for hydrocarbons with a pressure amplitude p1 = 2, 4 MPa in water with nitrogen bubbles with an initial gas content of α20 = 4. The processes of propagation and reflection of the shock wave from the rigid wall were analyzed with a change from α20 = 0, 5 to 6 % and the amplitude of the shock wave from 2 to 100 MPa [9–12]. The pressure range from 100 MPa to 100 GPa was considered in [13].

The paper [14] investigates the features of the dynamics of two-dimensional pressure waves of weak intensity in a layered bubble liquid. The effect of the initial bubble radius on the wave propagation is analyzed. The possibility of formation of pressure peaks near the boundary between layers is studied.

The work [15] considers reflection and refraction of acoustic waves at the interface between air and fog. The phase velocity and the sound attenuation coefficient for the fog, as well as the reflection and refraction coefficients for the normal and oblique incidence of the wave are calculated. The dependence of the refraction angle on the frequency and the angle of incidence of the acoustic wave on the interface between air and fog is studied. On the basis of the obtained analytical expressions and analysis of numerical calculations, it is established that in the case when the wave falls from the side of the fog to the interface, there is a critical angle of incidence such that, complete internal reflection occurs at full angles. It is shown that total internal reflection does not occur when the wave falls from the air side to the boundary between air and fog.

The paper [16] studies the reflection and refraction of acoustic waves at different angles of incidence on the interface between a vapor-gas-droplet system and air. From an analysis of analytical solutions, it was found that in the case of incidence on the interface from the side of the vapor-gas-droplet medium, there is a critical angle of incidence at which the wave is completely reflected from the boundary, i.e. total internal reflection takes place. It is shown that for a certain angle of incidence on the interface both from the air side and from the mixture side and for a certain volume fraction of water in the disperse system, complete transmission of the acoustic wave through the medium is observed.

In [17], the features of reflection and refraction of acoustic waves at the interface between pure water and bubbly water are investigated for the case of oblique incidence. From an analysis of analytic solutions, it follows that, for a wave incident on the interface from the side of a bubbly liquid, there exists a critical angle of incidence, which depends on the frequency and the parameters of the disperse system, that the wave is totally reflected from the interface at angles of incidence exceeding the critical one.

The works [18, 19] present the results of studies on the acoustic effects on multifractional mixtures of liquid with vapor-gas and gas bubbles of various sizes and different compositions with phase transformations.

The paper [20] numerically analyzes the influence of variations of equilibrium initial temperature of a system in the range from 300 to 373 for two initial bubble sizes a ₀ = 10 ^-6 and 10 ^-3 m. The effect of the perturbation frequencies on the reflection coefficient and refraction index at normal incidence was studied. It was shown that the condition of total internal reflection can be fulfilled by the incidence of a wave from a bubbly liquid at the interface.

The work [21] studies the characteristics of the reflection and refraction of harmonic waves at its “oblique” incidence on an interface between a “pure” liquid and liquid with bubbles filled with a vapor-gas mixture. For the considered problem, we obtained the dispersion equation and carried out a numerical analysis of the effect of the perturbation frequencies in the range 10 2 -10 7 s ^-1 on the dependence of the angle of refraction on that of incidence for three equilibrium initial temperatures. Also for the same reflection, we studied The dependence of the critical angle of incidence on the parameters of a two-phase system and the perturbation frequencies.

In [22, 23], maps of the stability regions of the investigated systems are constructed as functions of the degree of overheating of the liquid. The influence of the initial degree of overheating (from hundredths to one degree) and pressure increase on the evolution of harmonic waves is analyzed. For unstable systems, the dependence of the increment on bubble radius with increasing degree of water overheating is studied.

Analysis of the previous works shows that the intensity of attenuation of sound disturbances in the considered systems is mainly determined by the thermophysical characteristics of the gas in the bubbles. It turns out that these effects are greatly enhanced with an increase in the vapor concentration due to an increase in the temperature of the system.

1.    Governing Equations

Suppose that a liquid with the temperature T 0 and pressure p 0 contains spherical bubbles with the radius a 0 filled with vapor and gas insoluble in the liquid phase. Let us consider the propagation of small perturbations in the described system in a planar one-dimensional and one-velocity approximation. Assuming that the liquid is acoustically compressible, we can write the following linearized equation for the pressure p _l , velocity, and bubble radius oscillations [2]:

1 — a g o dp i

C _l ⁰    ∂t

₀ ∂v     ₀ α g 0 ∂a

+ ^{P i 0} dx — ^{3P i0} ^T dt

= 0,

where v is the velocity of the medium, a is the radius of the bubbles, and C _l ⁰ is the frozen speed of sound in the liquid, α _{g 0} is the volume content of the void fraction, ρ _l ⁰ ₀ is the dencity of phases in initial undisturbed state.

The momentum equation has the form

₀            ∂v   ∂p l

^{P i 0} (1 ^- O g o ) dt + dx = ^{0-                            (2)}

We assume that the perturbations of the pressure in the liquid p _l and in the bubbles

P g = P _u + P a are connected by the Rayleigh-Lamb equation. After linearization, we take

into account the capillary forces, and rewrite the Rayleigh–Lamb equation as follows:

₀ ∂ ² a     ρ _l ⁰ ₀ ν _l ^{( µ )} ∂a

^{P l 0 a o} дГ ^{+ 4} a dt

Here ν _l ^{( µ )}

2a

= P g - P i + —a-a ₀

is the kinematic viscosity of the liquid.

We write the equation of heat conduction and diffusion inside the bubble as well as

the heat equation in the liquid around the bubble to take into account the interfacial heat and mass transfer as follows:

W = Ddr ² IT (0 o), ∂t r²∂r ∂r

₀ dT‘    A i д ( ₂дТ!\   ,              - 1 / з_ч

Рю c^T = “2 Г r        (a ⁰ <^r< ao^a^) У               (5)

dt r ² dr у dr J                  g

The prime mark indicates that, in addition to x and t these parameters depend on the radial coordinate r counted from the center of a bubble. Here k is mass concentration of vapor phase, T _g , T _l , c _g , c _l , λ _g , λ _l denote the temperature, specific heat and thermal conductivity of the gas and liquid phases respectively, D is a coefficient of diffusion.

On the interface of phases (r = a ₀ ), we define the boundary conditions following from the conditions for the balance of heat and mass as follows:

′     ′            ′             ∂T l       ∂T g                 D ∂k ^′

T g ^T l     ^T , k    k ^{( a )} , ^A l dr ^{A g} dr    jl j 1 - k o I dr )

where l is specific heat of water vapor formation, j is a mass transfer intensity, T ( _a ) and k ( _a ) are perturbations of temperature and vapor concentration on the bubble surface, respectively.

For the gas pressure inside the bubble, we have:

■ = -3y>0■ +3(Y - 1)A dT^}   +3Yp«   B № dt         ao dt            ao \ dr Г r=ao     ao (1 - ko)Bgo \ dr

Y = c g o ^{/ ( c} g o ^— B o ),    c g o = c u k o ^— c a ^{(1 —} k o )-

For the initial undisturbed state, we write the following equation:

P s (T o )           B k o

pgo     Ba + (Bu — Ba^ko ’ which uniquely relates to the mass concentration of vapor in the bubble with temperature To. In order to determine ps(T), we use the formula ps(T) = p* exp(—T*/T), where p*, T* are the empirical parameters depended on the type of liquid.

• 2.    Dispersive Analysis

Let us find the solution of the above system in the form of a damped traveling wave: pl, pg, u, a ~ exp [i (Kx — ut)], T' = Ti(r) exp [i (Kx — ut)],   (i = g,l), k' = k(r) exp [i (Kx — ut)], K = k + i5, Cp = u/k, i = a/—1, where K is the wave vector, δ and Cp are the damping coefficient and the phase velocity of the wave, respectively. From the condition for the existence of a solution of this type, taking into account the acoustic discharge effects [24] of bubbles, we obtain the dispersion equation

^{K 2     (1 — a} g o ^{) 2} , _q^p i o ^a g o ^{(1 — a} g o )

=              + 3, u2       с 2

У =3^ —     — ^AvP u — 2Y(9)

Q s

. 2a ,     ,      . ,        ,ao pgo = po + —, С = 1 - iutA, tA = ao

Q = ^{1 +} (²r¹ Hkhyg ^{) +} r^kh^кЫ^(Ha + Tr^vh^m ^ , (io)

\ ko              1 — ko        / Vo   (1 — ko)e smh u(yi) J kh(x) = 3(x coth x — 1)x-2, sinh и (x) = 3 (1 + x

(A_ox tanh x(A _o - (A_ox - tanh x(A _o

A o = a,

- 1 / 3

g 0

П =

^{, ρ} l ⁰ 0 ^c 1

У 1 = \J - i^wa 0 ^/viT )

,

1) -    ) x ² or sinh и (x) = 3(1 + x)x ² ,

^{- 1))}

z = -i^a c /DD , ^e = ⁽ y ^- ^nH X ² ,

ρ _g ⁰ ₀ c g

c g T         B υ

X 7 ,   Hv    D ,   Ha lB0

B a

B 0

H = H u - H a .

For c ^ 0, dispersion equation (8) involve the following formula for the equilibrium velocity of sound:

C e =\l^~ f(1 - k o )H a + ko ρ ⁰ ₀ α g 0

α g 0 γ β

-

2 _^_

3 a o P ^o o a ₉ o ^,

which generalizes the well-known Malloch and Landau formulas [25]. In particular, at the boiling point T _o = T s (p _o ), taking into account the expressions from the dispersion equation, we obtain

C Ik (& V (Bo V ^l2  I ⁴ '

e V ^o   p oo      B u    CT ⁺ 3 a o P ?o a g o

.

3.    Numerical Results

Numerical calculations for water with vapor-gas bubbles were carried out on the basis of above-mentioned dispersion equation. The data from [26] were used as the values of the physical and thermophysical parameters. All calculations were carried out for a liquid under pressure p 0 = 0, 1 MPa.

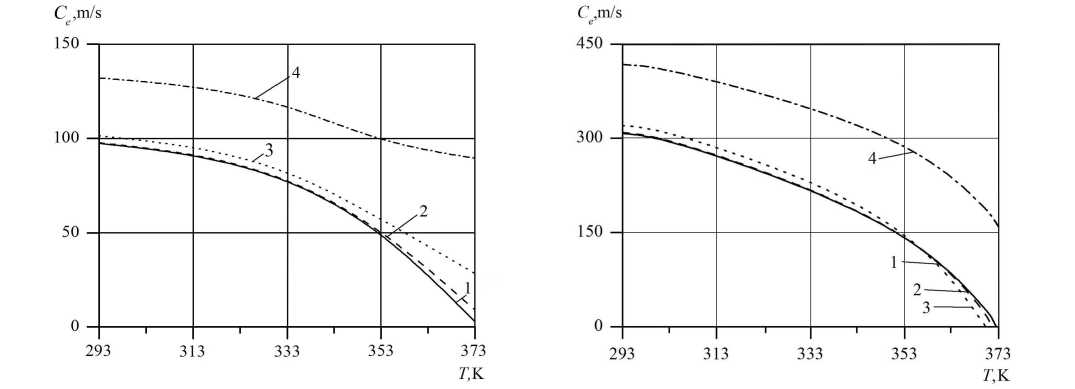
Fig. 1 . Dependence of the equilibrium speed of sound on temperature for a _{g 0} = 10 ^-2

Fig. 2 . Dependence of the equilibrium speed of sound on temperature for a _{g 0} = 10 3

Figs. 1 and 2 show the dependence of the equilibrium velocity of sound determined by equation (11) on the water temperature To for ago = 10-2 (Fig. 1) and ago = 10-3 (Fig. 2) under the condition c < c^') (c(T) = ViT)/(ao/a2/3). Lines 1, 2, 3, and 4 correspond to the values ao = 10-3, 10-4, 10-5 and 10-6 m. It is easy to see that the magnitude of the equilibrium velocity increases as the radius of the bubbles decreases. This is due to the increase in the “rigidity” of the bubbles depending on the capillary forces on the interphase surface and the phase transitions.

Fig. 3 represents the dependence of the phase velocity (a) and the damping coefficient (b) on the perturbation frequency for different values of the equilibrium temperature T ₀ and initial void fraction volume α g 0 = 10 ^-2 . The dashed line indicates the case of a coarse bubble media (a 0 = 10 ^-3 m), while the dotted line corresponds to a highly dispersed media (a 0 = 10 ^-6 m). Solid lines 1, 2 and 3 correspond to the values of equilibrium temperature T 0 = 300, 353 and 373 K. The diagrams show that with increase in the equilibrium temperature the phase velocity decreases approximately 2 – 3 times in the low-frequency zone (ω ≪ ω R , where ω R is the Minnaert resonance of the bubbles). According to the calculation results presented in (b), a sudden change of the damping coefficient δ is observed. In particular, for the frequency value ω = 10 ³ s ^-1 , the value of the damping coefficient δ increases from 10 ^-1 m ^-1 to 5 m ^-1 , and for the frequency value ω = 10 ⁴ s ^-1 the value δ increases from 1 m ^-1 to 10 m ^-1 . Analyzing the results obtained, we can conclude that, in the low-frequency zone, an increase in temperature from normal conditions to the boiling liquid improve weak perturbations damping by more than an order (tens of times).

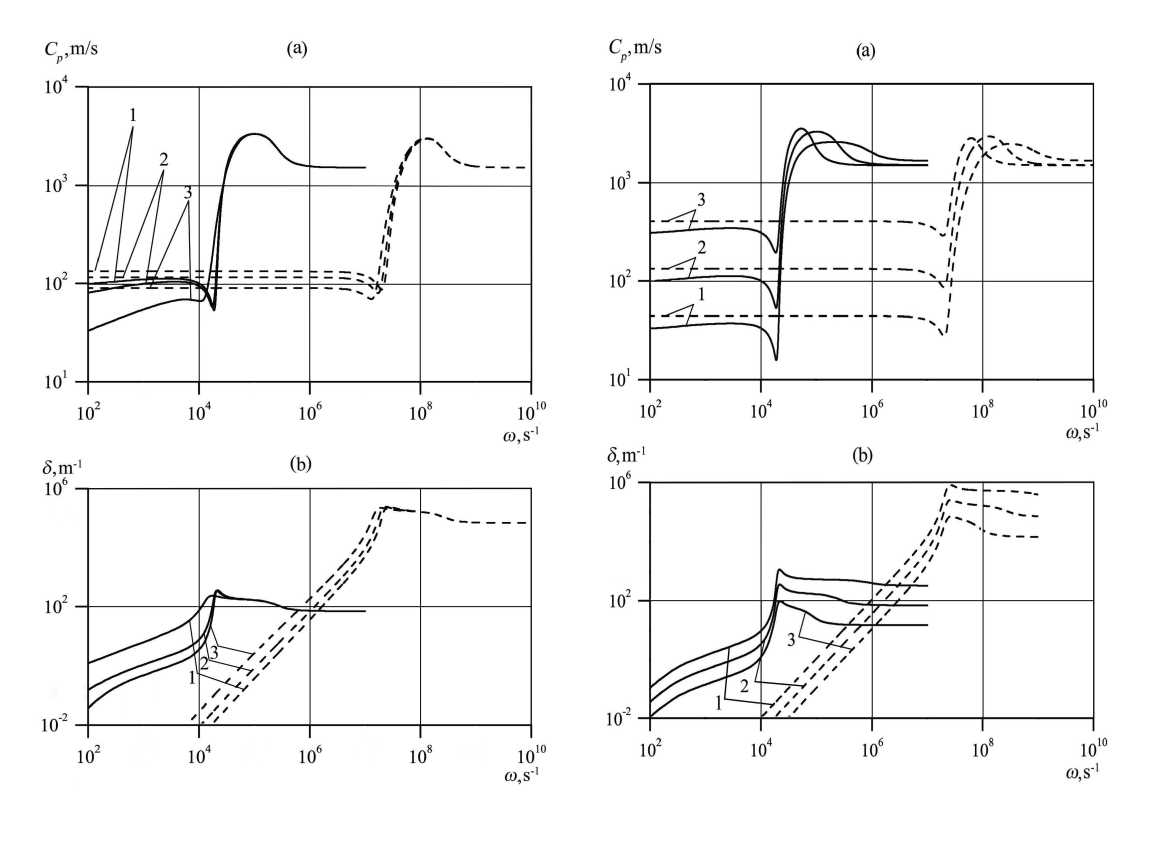
Fig. 4 . The dependence of the phase velocity (a) and the damping coefficient (b) on the frequency of the perturbations. 1 – α _g 0 = 10 ^-1 , 2 – α _g 0 = 10 ^-2 , 3 – α g 0 = 10 ^-3

Fig. 3 . The dependence of the phase velocity (a) and the damping coefficient (b) on the frequency of the perturbations. 1 – T 0 = 300 K, 2 – T 0 = 353 K, 3 – T 0 = 373 K

Fig. 4 shows the dependence of the phase velocity (a) and the damping coefficient (b) on the frequency of the perturbations for different values of the initial void fraction volume α g 0 at the equilibrium temperature T 0 = 373 K. The dashed line indicates the case of a coarse media (a 0 = 10 ^-3 m), while the dotted line corresponds to a highly dispersed media (a ₀ = 10 ^-6 m). Solid lines 1, 2 and 3 correspond to the values of volumetric contents α _g0 = 10 ^-1 , 10 ^-2 and 10 ^-3 . The diagrams show that with a decrease in the volumetric content the phase velocity increases approximately 5 times in the low-frequency region (ω ≪ ω R ). Note that, in the low-frequency region a small increase in the phase velocity from the disturbance frequency is also characteristic for a coarse media, while the phase velocity is constant for a highly dispersed media. It takes place because of the role of phase transitions increases in the low frequencies. Due to phase transitions vapor – gas bubbles with a small mass content of an inert gas become less elastic. In the considered case, the elasticity of the bubbles is mainly determined by the mass content of the gas. In the zone where the frequency of the external perturbation is comparable with the Minnaert resonance of the bubbles (ω ∼ ω R ), a strong increase in the phase velocity occurs. Moreover, the larger the initial volumetric content of bubbles, the greater the change in phase velocity. Similar pictures are observed for the damping coefficient.

Conclusion

For the cases considered, it is established that as the bubble radius decreases the equilibrium velocity increases. This is due to the increase in the “rigidity” of the bubbles, which depends on the capillary forces on the interphase surface and the phase transitions.

The study of harmonic waves in a liquid with vapor-air bubbles of the fixed sizes shows that the damping coefficient varies insignificantly when the initial gas volumetric content α _g0 changes from 10 ^-3 to 10 ^-1 at the equilibrium temperature T ₀ = 373 K near the low frequencies (ω ≤ ω R ).

Also, it was also found that with a decrease in the volume content the phase velocity increases approximately 10 times in the low-frequency region (ω ≪ ω _R ) and the damping coefficient δ decreases with decreasing α _g0 .

Acknowledgment. The work was supported by the state budget for the state task for 2019-2022 years (project 0246-2019-0052).