Acoustooptic shutter for glass units

Original article

Despite the variety of existing liquid crystal (LC) devices, scientists around the world continue to search for solutions to scientific theoretical and experimental problems, engineering projects to develop new generation information display systems, as well as optical devices. The use of liquid crystals is attractive in this sense due to the small size of devices, low power consumption, simplicity of design, low cost, easy controllability of liquid crystals by various external fields (mechanical, electrical, magnetic, thermal).

Liquid crystals are used as a matrix for doping with various nanoagents [1, 2] using the guest-host effect, which change the physical and chemical properties of the working substance. There is a search for options for the

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS quality of the surface of the electrodes and their processing for the creation of light filters, light intensity regulators, light-oriented lenses [3], the simultaneous influence of, for example, electric and magnetic fields is being studied [4]. In paper [5], the formation of a molecular crystal in the volume of an nematic liquid crystal (NLC) in the vicinity of the p-n junction was considered, the birefraction of which can be controlled by an electric field. Researchers are looking for new piezoelectric materials and effects to create sensors, transducers, and frequency controllers [6]. The article [7] theoretically studies the conditions for the formation of spatially modulated phases due to the action of a flexi pair in condensed media and liquid crystals. Computer modeling has shown common features of ferroics and liquid crystals. In both substances, spatially modulated structures are formed. Similar properties will give more opportunities in terms of the practical use of these substances. The authors of papers [8, 9] studied the direct flexoelectric effect in the vicinity of the phase transition from the nematic phase to the isotropic one, as well as the parameters affecting the nature of the flexoelectric polarization. In [10], the authors studied the orientational instability of a liquid crystal director in a flat flexoelectric cell in a constant electric field applied normally to the cell surface. It has been found that under a quadratic action of an electric field, the orientational instability is threshold, but non-threshold under a linear action. Using the elastic properties of LC and introducing additives into its volume, the relationship between flexoelectricity and mechanotransduction was studied [11]. Liquid crystals are used in the search for solutions to a number of applied and fundamental problems [12–37], which is justified by the economic and technological components.

Thus, the analysis of scientific works of recent years shows an interest in the issue of studying the phenomena and effects associated with flexoelectricity in liquid crystals and in materials similar in properties. Under the action of mechanical shear, the liquid crystal layer is deformed, as a result of which surface polarization occurs. This paper presents the results of an experimental study of the effect of an electric field on this surface polarization. The article is devoted not only to the study of flexo-electricity in condensed media, but it is also proposed to use the flexoelectric effect to create an acoustooptic switch based on liquid crystals for double-glazed windows. When, with one orientation of the molecules of the liquid crystal, the light flux passes through the cell, but not with the other. Also, the results obtained are relevant for the implementation and development of memory devices in nanoelectronics and LC monitors of a new generation.

MATERIALS AND METHODS

Materials

Liquid crystals with a homeotropic orientation of the director were used: n – methoxybenzylidene – n-butylaniline (MBBA) with ε _α < 0; 4 – octyl – 4-cyanobi-phenyl (OCB) with ε _α > 0; nitrophenyloctyloxybenzoate (NPOOB) with ε _α > 0; cyanophenyl ester of heptylbenzoic acid (CPEHBA) with ε _α >> 0, which were in the nematic phase. The main parameters of liquid crystals are presented in Table 1.

Methods

The cell was a flat capacitor, it was assembled from two plates, between which the LC under study was placed. One of the plates was thin, it was connected to the vibration source by means of a waveguide about 10 cm long and 0.5 mm thick. The frequency range of oscillations is from 20 Hz to 20 kHz. In our case, the exposure frequency was 1 kHz. The LC thickness could be changed using a micrometric screw (layer thickness h from 10 to 100 µm). The cell was placed in a thermostat to main-

Тable 1

Basic physical parameters of liquid crystals

Liquid crystal	Mesophase temperature, оC	е 11 , 10–4 un. CGS/ cm	е33 , 10–5 un. CGS/ cm	Dipole moment, p , D	Dielectric anisotropy, εα
cyanophenyl ester of heptylbenzoic acid (CPEHBA)	К 45 о N 56 о I	5,5	3	~4,5	~19
nitrophenyloctyloxybenzoate (NPOOB)	К 45 о А 61о N 68о I	5,0	1,0	~4,1	>0
n-methoxybenzylidene – n-butylaniline (MBBA)	К 18 о N 42 о I	4,5	102	~2,6	~-0,56
4-octyl – 4-cyanobiphenyl (OCB)	К 22,5о С 34 о N 4 1,3 о I	6,0	1,0	~5,0	~9

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

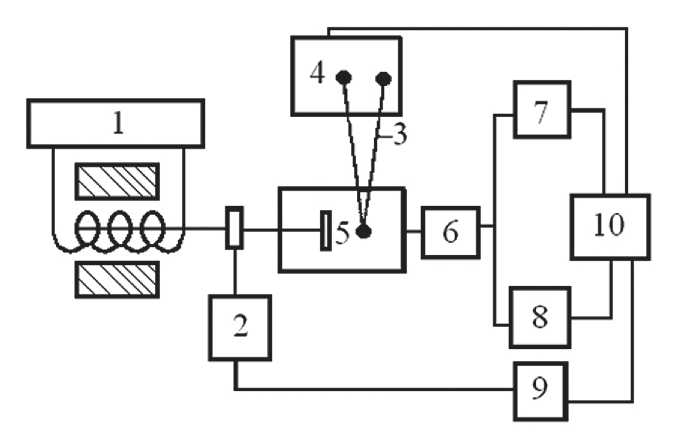
Fig. 1. Block diagram of the experimental setup: 1 – sound generator; 2 – selective voltmeter; 3 – differential thermocouple; 4 – DC microvoltmeter; 5 – thermostat with LC cell; 6 – preliminary charge-sensitive amplifier;

7 and 8 – selective amplifiers; 9 – phase difference meter; 10 – analog converter

tain the required temperature, which was controlled by a thermocouple [35].

For an experimental study of the effect of an electric field on the polarization induced by acoustic action, an experimental setup was assembled (Fig. 1). The main element of its recording part is the amplifying path, which consists of a charge-sensitive amplifier with a high input resistance of 10 GΩ and a selective amplifier (2 MΩ). The charge-sensitive amplifier in the studied frequency range had a gain of 2 ⋅ 10², as well as a relatively low noise level of about 50 µV. It provides for the possibility of applying a polarizing bias voltage U _c to the sample in the range from 0 to 2 ⋅ 10³ V. The selective amplifier made it possible to record electrical signals in the range of 20 – 105 Hz, the lower level of which is 4 ⋅ 10^-2 µV, and the upper level is 1 V.

The design of the amplifier makes it possible to apply a constant voltage of up to 100 V to its input, as well as linear and synchronous detection of signals, which were then fed to the ADC that records them. If it was necessary to simultaneously analyze and study the spectral composition of the signal under study, two paths were used, each of which, independently of each other, made it possible to process spectral harmonics.

Let us now turn to the analysis of the process of measuring electrical signals according to the method described above. Since the investigated anisotropic molecular liquids – liquid crystals are weak electrolytes (imperfect dielectrics) and have a sufficiently high impurity conductivity σ, it will significantly affect the process of measuring the magnitude of signals induced by orientational perturbations.

Consider a dielectric with an average permittivity <ε> and conductivity σ. Let us assume that, due to some reasons, a charge of density σ appeared in its volume, which is compensated by its own conduction mechanism for the characteristic time τ = <ε> ε _o σ^–1 [34]. In the case of liquid crystals, the process of compensation and charge transfer is determined by the physicochemical mechanism of dissociation and recombination of impurity conduction ions. In weak electric fields, when the time of passage of ions between the electrodes:

τ = 2η(µ ₊ + µ_)^–1 E ^–1,                          (1)

(where h – LC layer thickness; µ ₊ and µ _– – charge carrier mobility; E – potential gradient) much longer than the recombination time, the current-voltage characteristic of the liquid crystal is linear with respect to the field; therefore, one speaks of the electrical conductivity constant σ.

If, as a result of the orientation perturbation of the LC layer, the polarization P is generated, then for the charge Q = ʃ P dS , induced on the capacitor plates, equivalent to a cell with a capacitance, one can write the relaxation equation:

dQ / d τ = ℰ / R – Q / C ,                         (2)

where ℰ – emerging emf; R – ohmic resistance LC; τ = <ε> ε _o σ^–1 – relaxation time.

Let us assume that <ε> = ℰ (ω) ℰ ^iωt and Q = Q _ω ℰ ^iωt , then for Q _ω the next solution is obtained:

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

Q _ω = τ/( P ℰ _ω (1+ω² τ²)^–1),                        (3)

where ℰ _ω – EMF value, determined by the polarization mechanism and depending on the perturbation frequency.

Thus, in reality, the value will be measured:

ℰ ' = ωτ ℰ (τ)/(1+ω² τ²).                           (4)

It follows from the last expression that at low frequencies ω << τ^–1 the measured EMF is defined as ℰ ’ = ωτ ℰ (τ), which reflects the process of masking the LC polarization by conduction ions. In the frequency range ω ≥ τ^–1, the EMF is defined as follows: ℰ ’ ~ ℰ /ωτ, this corresponds to dielectric losses that increase with increasing excitation frequency.

RESULTS AND DISCUSSION

The behavior of charges induced on the surface of a liquid crystal due to internal mechanisms of molecular orientation polarization depending on the magnitude and direction of the external electric field E will be considered. To do this, an LC layer (εα < 0) with an initial homeo-tropic orientation, for example, an MBBA, will be placed in an electric field. In this situation, when the director n and the electric field E are colinear, as is known [34], a number of structural-phase transformations of the type of the Freedericksz effect occur, electrohydrodynamic instability (EHDI). It should be expected that the orientational transitions and the electric field itself will affect the magnitude and behavior of the recorded harmonics U1ω and U2ω, for at least two reasons: first, when the orienta- tion changes (appearance of a director tilt to the surface), there is a contribution to the total polarization bend – deformation (flexocoefficient e33), which has a slightly higher value than e11 [36]; secondly, the electric field polarizes the medium. Indeed, with an increase in the polarizing voltage Uc on the plates of the cell representing the capacitor, the values of the harmonic signals U1ω and U2ω first increase, and then, after reaching a minimum, they enter a linear section of the dependence on the field, which is due to the capacitor effect. It is necessary to take into account this contribution in the dependences; it appears due to a change in the thickness of the LC layer during periodic oscillations of one of the cell surfaces. It can be measured experimentally by converting the mesophase to an isotropic state. In this case, this value will depend on the plate oscillation amplitude a and the average permittivity <ε>=(ε‖+2ε┴)/3 and slightly differs from the similar value in the mesophase.

The dependences of the harmonics U _1ω and U _2ω on the field should be analyzed (Fig. 2). Their values are sensitive to the direction of the electric field, that is, when a positive potential is applied to a deformable plate, the harmonics reach lower values than with a negative one.

This is due to two reasons: on the one hand, the electric field at a positive potential stabilizes the molecules of the polarized layer (in MBBA they are directed with their negative end to the surface [34]), and at a negative potential it makes it less stable, which in one case leads to a decrease in the tilt angle by surface, and in the other – to its increase, which leads to an increase in the second harmonic. On the other hand, as shown in [36], under weak boundary conditions, polar deformation can be realized in the NLC volume. In this case, a similar situation

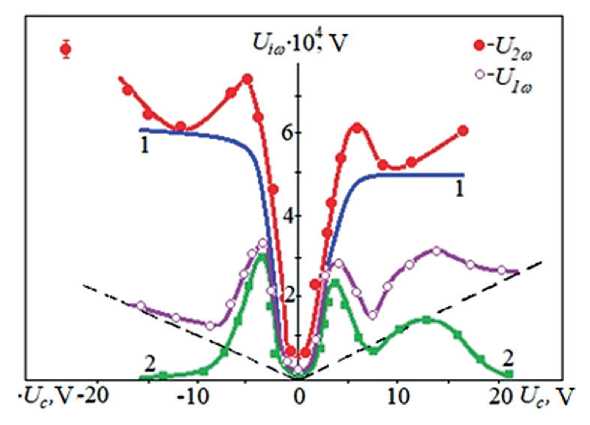
Fig. 2. Dependences of the values of the first U _1ω and second U _2ω harmonics on the bias voltage U _c:

1 – U _2ω without the contribution of the capacitor effect; 2 – U _1ω (dashed straight line – contribution of the capacitor effect; MBBA ε _α < 0 a = 0.2 µm; h = 15 µm; ω = 1 kHz)

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

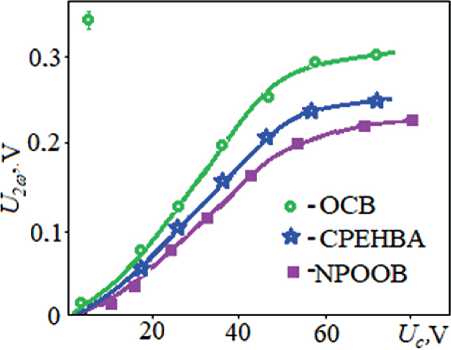
Fig. 3. Field dependences of the second harmonic U _2ω in NLC with ε_α >> 0 ( a ≈ 0.3 µm; h = 15 µm; OCB at T _N = 35°C; CPEHBA at T _N = 48^оC; NPOOB at T _N = 63^оC)

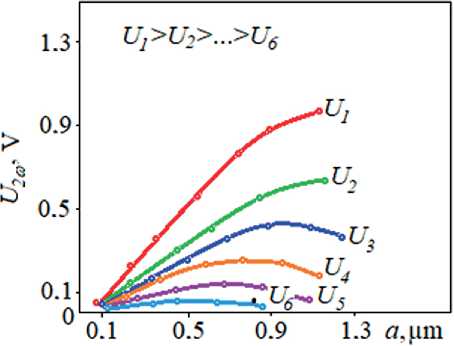
Fig. 4. Dependences of the value of the second harmonic U _2ω on the amplitude of the action at different polarizing voltages: U ₁ = 90 V; U ₂ = 60 V; U ₃ = 40 V; U ₄ = 30 V; U ₅ = 20 V; U ₆ = 10 V ( h = 15 µm)

takes place due to the non-equivalence of the surfaces, which arises as a result of the induction of surface angles θ _σ (– E , a ) ≠ θ _s ( E , a ) by acoustic perturbations and the electric field. In addition, the signals U _1ω and U _2ω , regardless of the polarity of the field, reach their maximum in the vicinity of the Freedericksz transition. The decrease in the signals then is a consequence of the development of the EHD instability, the structure of the liquid crystal becomes finely dispersed with the wave vector q ’>> q _2,3 ( q _2,3 is the vector that determines the orientational deformation), which leads to the suppression of the flexo effect.

Along with the considered reasons for the change in the values of harmonics U _iω due to reorientation mechanisms, it is necessary, apparently, to take into account the polarization effects of amplification of the recorded signals. In this case, the induced orientational molecular polarization is recorded as a result of its periodic modulation in the volume. A similar effect can be registered in the absence of parasitic phenomena such as the Freedericksz transition and EGDN. This is possible in LCs with a large anisotropy of the permittivity (ε _α >> 0). Moreover, using the analogy with surface polarization, the largest value of the recorded signal should be observed at the second harmonic, since U _2ω ~ P _V < θ _d ² > exp( i 2ω t ) ( P _V – bulk polarization). Studies confirm this assumption: the ratio between the harmonics U _1ω ^max: U _2ω ^max<< 1 takes place in all studied nematic liquid crystals. In contrast, in A - and C -type smectic liquid crystals U _2ω ~ U _1ω , that is, U _2ω is much less than in nematics.

The behavior of harmonics U _iω in an electric field should be analyzed in more detail. When a field is applied to a homeotropic layer of NLC, for example, CPEHBA ( h = 15 µm; a = const; ω = 1 kHz), the value U _2ω linearly increases from the voltage U _c up to reaching “saturation”

(Fig. 3), which is due to an increase in stabilizing dielectric moment over the viscoelastic one.

Accordingly, the value of U _2ω in this case is 1.5 ⋅ 10³ – 2 ⋅ 10³ times greater than without an electric field. If we consider the dependences of U _2ω on the disturbance amplitude a at fixed values of the electric field (Fig. 4), then it should be noted that at low fields ( Е ≤ 10⁴ V/cm), the value of U _2ω first increases and then decreases due to an increase in the tilt angle of the director relative to surface normal and transition to turbulent motion in the layer. At relatively high fields Е ≤ 5 ⋅ 10⁴ V/cm, such a state is not achieved. The value of the signal U _2ω in this case is ~1 V ( a ~ 1 µm). In the nematic phase of NPOOB and OCB, the second harmonic U _2ω has approximately the same order (Fig. 4), although in cyanobiphenyl it is somewhat higher, which is apparently explained by the large dipole moment of its constituent molecules.

Thus, as a result of the application of an electric field to the homeotropic NLC layer, polarization increases in the crystal volume, the presence of which is recorded by means of orientational modulation and measurements of the charges induced on the conducting substrates.

To exclude alternative explanations for the appearance and increase of U _2ω in fields, studies were carried out of its behavior on conductivity σ (the mechanism of orientational polarization – its anisotropic part), dielectric anisotropy ε _α , and thickness of the liquid crystal layer h . Model experiments were carried out on CPEHBA and its mixtures with NLC MBBA. When doped with ionic additives, the value of the signal U _2ω decreases due, apparently, to the screening effect. This means that the contribution of this mechanism is negligible (Fig. 5a).

Changing the anisotropy of the mixtures ε _α > 0 from 20 to 0.05, the U _2ω value was measured at the same polar-

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

а)

b)

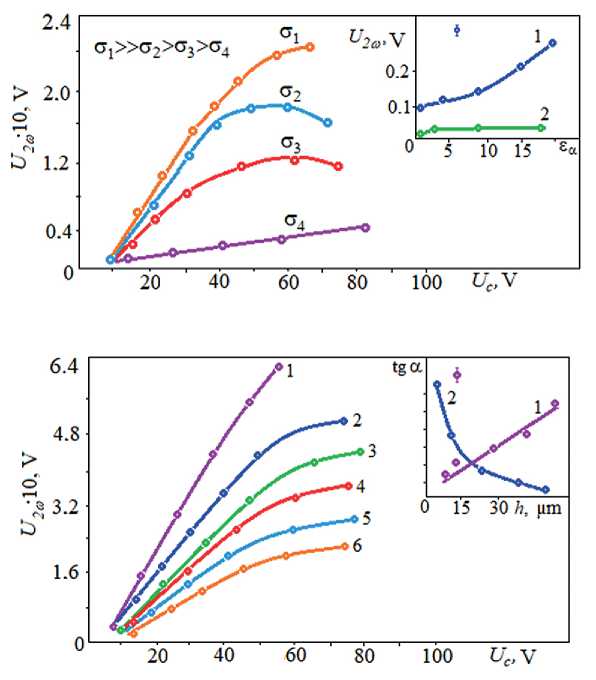
Fig. 5. а) Field dependences of the second harmonic U _2ω (CPEHBA) at different initial conductivity of the samples σ ( a ~ 0.3 µm; h = 15 µm); inset – dependences of U _2ω on dielectric anisotropy ε_α (1 – experiment; 2 – theory);

b) field dependences of the second harmonic U _2ω (CPEHBA) at different thicknesses of LC films (1 – h ₁ = 70 µm; 2 – h ₂ = 55 µm; 3 – h ₃ = 45 µm; 4 – h ₄ = 30 µm; 5 – h ₅ = 15 µm; 6 – h ₆ = 10 µm); inset – dependences of the tangent of the slope of the curve U _2ω( U _c) on the thickness h (1 – experiment; 2 – theory)

izing voltages and perturbation a depending on the value of ε _α (Fig. 5b). The signal due to the dielectric mechanism in this case will be U _2ω ~ ε_‖ E < θ _d ² > /ε_┴.

According to this relation, with a large anisotropy ε _α , the functional dependence U _2ω (ε _α (at E = const) becomes asymptotic – a straight line parallel to the abscissa axis ε _α , and for small ε _α << 1, the signal value will tend to zero, as shown in Fig. 5b. In contrast to this, in practice, the value of the signal U _2ω for ε _α << 1 does not tend to zero, and for ε _α >> 1 does not reach the above asymptotics.

But it is obvious that the contribution of the dielectric permittivity is not equal to zero and, according to estimates, is about 10–15% of the recorded value U _2ω . The results of measurements of the value of the second harmonic on the thickness of the NLC layer (Fig. 5b) showed that the tangent of the slope of the dependence U _2ω to the abscissa axis Uc increases with the thickness h , while with the dielectric modulation mechanism the value tgα ~ h ^–1 (so as U _2ω ~ E = U/h, then tgα ~ U _2ω /U ~ h ^–1).

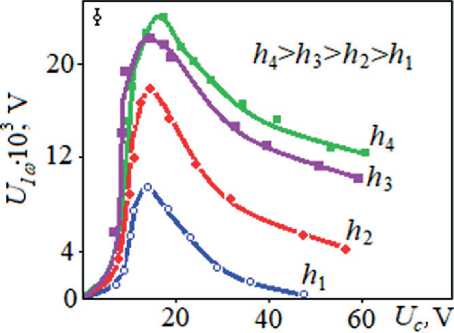
The behavior of the first harmonic in an electric field should be discussed, the CPEHBA has been stud- ied in detail. The perturbation amplitude, for example, a ~ 0.3 µm should be fixed and the dependence U1ω (Uc) for this deformation should be analyzed (Fig. 6).

At low polarizing voltages U _c ≤ 15 V ( h = 15 µm), the dependence U _1ω is approximated by a power function of the U _c ⁿ type (where n ~ 3); at U _c >> 15 V the second harmonic U _2ω depends as U _c ^-1. Qualitatively, this behavior can be explained by a change in the amplitude of the director oscillation, which follows from the formula for the phase difference:

2тт f^/2 2ттй

8 = — An(z)dz =—— < An(z) >, (5) ^A J-h/2

where <∆n(z)> – averaging over the thickness of the crystal layer; h is the LC thickness; λ is the wavelength of light.

Considering the term describing the acting field ε _α ( En )²/4π, in the initial equations, then the deviation amplitude of the LC director can be approximately written [34]:

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

n P^yo

9 =---exp

П1Ч

' V2 '

--q(z-S)

cos

V2 ' — q(z-S)

COStit, (7)

Fig. 6. Field dependences of the first harmonic U _1ω for different sample thicknesses h ( a = const, ω = 1 kHz): h ₁ = 15 µm; h ₂ = 30 µm; h ₃ = 45 µm; h ₄ = 55 µm (CPEHBA)

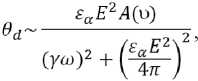
where A (υ) – function of the oscillation velocity of one of the surfaces and volumetric gradients υ( z , r ).

In this case, the magnitude of the first harmonic signal U _1ω is proportional to the thickness of the LC and the angle of deviation of its director U _1ω ~ e ₁₁ h θ _d , that is, under the condition γω >> ε _α E ²/4π (small fields), a power dependence will be U _1ω ~ U _c ³. In the case when γω < ε _α E ²/4π, it will be U _1ω ~ U _c ^–1.

Thus, in low fields, the signal increases due to the amplification of the director oscillation amplitude, but at a certain critical field E = (4πγω/ε _α )^1/2 it is suppressed, since the layer is stabilized by a constant electric field.

Previously, it was established [8, 9, 12, 13, 16, 22, 25, 28] that during periodic shear oscillations of one of the substrates limiting the liquid crystal, an EMF arises in the crystal layer due to both the flexoelectric polarization mechanism and the surface polarization modulation mechanism by acoustic vibrations. In this paper the influence of an external electric field E on the behavior of the first U _1ω and second U _2ω harmonics induced by the shift will be considered. In the general case, the behavior of the first harmonic in the studied substances is similar to the behavior of U _1ω excited by bending vibrations of one of the liquid crystal surfaces. However, the field dependences U _iω also have their own specific features associated with the symmetry of the perturbation and its spatial localization.

According to the solution for the distribution of the angle of deviation of the director from the normal to the cell θ along the z coordinate, in general terms, can be written:

where η ₁ – viscosity coefficient; q – the real part of the roots of the characteristic equation; ρ – the charge density; S – the distance at which the director deviates from the equilibrium position; ω – the oscillation frequency; υ _o – the speed at z = 0) the oscillating electrode is a source of a rapidly damping elastic-viscous wave with the wave vector | q | > h^–1 (h is the thickness of the actually studied layers 10 ≤ h ≤ 100 µm). For example, in an MBBA NLC, at the initial homeotropic orientation of molecules, a perturbation with the wave vector | q | ~ 3·10³ cm^–1, which makes the spatial scale of their localization about 3·10^–4 ÷ 5·10^–4 cm, and this value is less than the liquid crystal thickness (h ≈ 20 µm). It follows that under weak boundary conditions, we can assume that the main role will be played by orientational surface perturbations.

The field dependences of the first U _1ω and second U _2ω harmonics at low bias voltages, for example, in nematic liquid crystals MBBA and CPEHBA (Fig. 7) will be considered, and the sign of the field relative to the direction of the vibrational velocity gradient ∂υ _x /∂z will be varied. This gradient is not parallel to the normal vector to the surface of the oscillating plate-substrate.

Note that the position of the minima of the values of the first U _1ω and second U _2ω harmonics does not coincide with the zero point along the abscissa when U _c = 0. The harmonics U _1ω and U _2ω have a maximum when a positive potential is applied to the moving electrode. We also note that the characteristic polarizing voltage is U _c ~ +1 V, at which the harmonics U _1ω and U _2ω are minimal.

The behavior of the component harmonics U _iω within the framework of the approach outlined earlier should

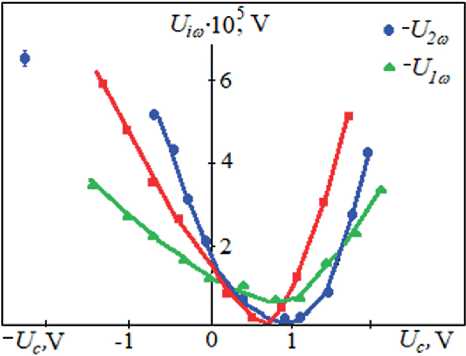
Fig. 7. Field dependences of the values of the first U _1ω and second U _2ω harmonics at low polarizing voltages (solid lines – MBBA at T _N = 24^oC; dotted lines – CPEHBA at T _N = 48^oC)

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS be discussed. To do this, first, the behavior of the second harmonic of the signal U2ω should be analyzed. In the absence of a field, the value of the second harmonic according to the formula

U 2ω = ∫ 0 ^h P s ( z )( ) <θ d ²> dz = P s S <θ d ²> cos<θ o > =

= U _s cos<θ _o ><θ _d ²>, (8)

where P _s – surface polarization value; U _s = P _s S – voltage drop on the surface layer; <θ _o > – the average value of the stationary tilt angle of the director; <θ _d ²> – the square of the average value of the angle characterizing the director oscillations) is proportional to the tilt angle of the director on the surface <θ _o > and the value of the surface polarization P _s , the vector of which has a certain direction relative to the substrate. The latter is the reason for the asymmetry in the field dependence U _2ω .

If the direction of the external field coincides with the direction of the surface polarization, then the total recorded signal:

U 2ω ~ S ef P s <θ d ²> – P V S ^–2<θ d ²>, (9)

where S _ef – effective surface polarization thickness; P _V – orientational polarization induced by an external field.

Or can it be written more simply:

U 2ω ~ U s <θ d ²> – U n ( Sh )^–1<θ d ²>. (10)

From this it is clear that with an increase in the external polarizing voltage, the value of the second harmonic U _2ω will have a minimum. In the opposite case, when P _s and P _V have the same direction, the signal U _2ω increases, which is confirmed by experiment.

In particular, this result makes it possible to determine the orientation direction of the molecules of the surface layer, i.e., the surface polarization, and to estimate the voltage drop U _δ on this polarized layer from the position of the minimum. In the case of NLC MBBA, the molecules are directed with their negative end to the surface, and the value of U _s ~ 1 V. For NLC CPEHBA, U _s ~ 0.7 V, and the molecules of this crystal are also directed with their negative end to the surface.

The asymmetry of the first harmonic signal U _1ω is closely related to the presence of surface polarization. The solution of this problem presents significant difficulties and, in the general case, is non-linear [31]. However, it can be shown that such an asymmetry arises even in the linear approximation. Since the perturbation is localized near the surface of the oscillating electrode, the moment conditions on the surface can be used [36]:

W (<θ _d > – <θ _o >) + k (∂<θ _d >)/∂z =

±( e ₃₃ P _s ) E , (11)

where e ₃₃ – flexoelectric coefficient. The signs are chosen depending on the direction of the field relative to the substrate and the direction of the polarization vector. Assuming that θ is small and <θ _d ><< <θ _o > (<θ _d > is the director oscillation angle on the surface). Then in (11) one can substitute an approximate solution of type (7) when θ _d ~ θ _d ’exp( iqz ). From here at z = 0 for the angle can be get:

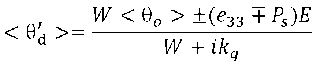
or at k _q >  W :

-

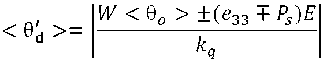
It follows from this expression that the value of the angle of oscillation of the director will depend significantly on the ratio of the value of the flexoelectric coefficient e ₃₃ , the value of the surface polarization P _s , and the sign of the field. That is, in one case the LC structure stabilizes, in the other case it is less resistant to external disturbances.

As applied to a specific case, for example, to a nematic liquid crystal MBBA, the following picture can be seen. Since the dipole molecules are directed with their negative end to the surface, in the case when there is a positive potential on the surface, it can be written in the following way:

d > ~ W o > + ( e 33 - P s ) E l,                (14)

when there is a negative potential:

d > ~ | w o > + ( e 33 - P s ) E |,                 (15)

Thus, in the region of positive displacement voltages, the molecules are stabilized, and at negative voltages, the molecules are less resistant to orientational perturbations, under the condition | e ₃₃ | < | P _s |.

Next the behavior of the recorded signals of the first U _1ω and second U _2ω harmonics at high polarizing voltages should be considered. The behavior of the first harmonic U _1ω in this case is similar to the behavior of the first harmonic excited during bending vibrations [8, 9, 12, 16], so this question is of no independent interest.

The study of the influence of an external electric field on the magnitude and change of the second harmonic should be considered in more detail. The study will be carried out on the example of NLC CPEHBA. A distinctive feature of the influence of the electric field E in the case of shear oscillations is that the second harmonic U _2ω reaches its maximum value in the low-frequency region ω ~ 100 Hz (Fig. 8), while in the case of bending oscillations, the frequency regression of the second harmonic begins in the kilohertz range.

From the frequency dependence U _2ω (ω) (υ = const) it follows that the value of the second harmonic U _2ω sharply

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS

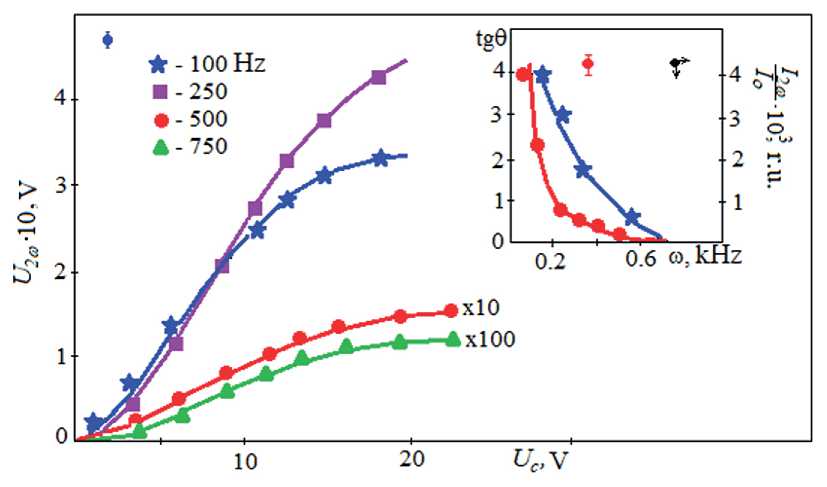
Fig. 8. Field dependences of the value of the second harmonic U _2ω at different perturbation frequencies ω (CPEHBA at T _N = 48^oC); inset – frequency dependences of the slope tangent tgθ and the magnitude of the acoustooptic effect I 2ω / I o

decreases with the frequency of the perturbation (Fig. 8). For example, the values of the second harmonic at ω ~ 100 Hz and at ω ~ 750 Hz at a given value of the bias voltage differ by 5·102 times. A possible reason for this change is the localization of the orientational perturbation near the oscillating electrode with increasing frequency. Since initially, according to the equation [35], the phase difference:

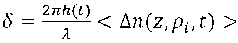
where h – LC layer thickness; λ – optical wavelength) perturbation wave vector | q | >  h ^–1 and with increasing frequency, the characteristic area of perturbation S ~ | q |^–1 ~ ω^1/2 and at a frequency of 1 kHz can be S ~ 10^–4 cm.

The latter is confirmed by the study of the frequency dependence of the magnitude of the second harmonic of the optical signal I _2ω / I _o under the simultaneous action of the polarizing voltage (Fig. 8). The acoustooptic effect, which consists in the modulation of the light flux polarized in the light transmitted through the cell, is strongly weakened with increasing frequency ω, and is not observed at all at a frequency ω ~ 1 kHz.

CONCLUSION

Thus, the influence of the action of an electric field on the surface polarization arising due to the flexoelectric ef- fect was experimentally studied in the article. It was found that the harmonics of the flexoelectric signal depend on the direction of the electric field; when a positive potential is applied to the movable plate, they take on smaller values than with a negative one. Under the action of weak fields, the magnitude of the signal at the excitation frequency is directly proportional to the amplitude of the oscillations of the liquid crystal director, and increases due to its increase.

It is theoretically substantiated that under weak boundary conditions, the main role is played by orientational surface influences. The sign of the electric field can be varied with respect to the direction of the vibrational velocity gradient. It was found that the values of the first and second harmonics take on a maximum when a positive potential is applied to the moving electrode. The characteristic polarizing voltage at which the U _1ω and U _2ω harmonics are minimal is U _c ~ +1 V. The asymmetry of the U _2ω dependence on the applied field is explained by the proportionality of the director tilt angle on the surface <θ _o > and the surface polarization P _s . It was also found that the LC molecules (MBBA and CPEHBA) are directed with their negative end to the surface of the cell substrate.

The obtained research results can be used in the development of pressure sensors, seismic sensors for buildings and structures, light modulators, as well as an acoustooptic shutter for double-glazed windows.

RESEARCH RESULTS OF SCIENTISTS AND SPECIALISTS