Адаптация алгоритмов роевой оптимизации к решению поисковых задач роевого интеллекта

Актуальной проблемой в области роевой робототехники является разработка алгоритмов управления такого рода распределенными системами [1, 2, 3]. Сложность данной задачи заключается в том, что целью алгоритма должно быть некоторое желаемое коллективное поведение всего роя, в то время как реально программируется поведение (одинаковое) отдельных роботов. Вместе с тем, имеется ряд задач поискового типа, например, задачи поиска источника загрязнения, которые могут рассматриваться, как оптимизационные задачи, для решения которых существует хорошо проработанный класс алгоритмов роевой оптимизации. Такие алгоритмы, как метод роя частиц, алгоритм бактериального

Сетевое научное издание «Системный анализ в науке и образовании» Выпуск №3, 2019 год поиска, муравьиные алгоритмы, изначально были спроектированы на основе моделей роевого поведения [4, 5]. Однако непосредственное применение таких алгоритмов в роевой робототехнике оказывается невозможным по причине использования ими механизмов, которые не могут быть поддержаны реальными роботами (размножение, отбор и т.п.). Кроме того, сама задача поиска того или иного объекта на заданной территории может ограничивать даже обычное поведение роботов – например, наличие препятствий (стен) мешает перемещению роботов даже на небольшое расстояние. Такие ограничения в оптимизационных задачах обычно отсутствуют. Целью данного исследования является адаптация алгоритмов роевой оптимизации к решению поисковых задач роем роботов.

В настоящей работе рассматривается модельная задача поиска источника некоторого сигнала, описываются адаптированные версии нескольких классических алгоритмов роевой оптимизации, описывается программная реализация системы моделирования рассматриваемого класса алгоритмов, приводятся результаты численного исследования эффективности разработанных алгоритмов.

Модельная поисковая задача

В данной работе рассматривается следующая поисковая задача. В двумерной области имеется источник некоторого сигнала. В заданной области также присутствуют различные препятствия, представляемые в виде прямолинейных стен, мешающие прохождению сигнала (рис. 1). Предполагается, что сигнал монотонно убывает с увеличением расстояния до целевой точки (т.е. до источника сигнала) с учетом наличия препятствий. Поэтому для простоты в качестве целевой функции было выбрано расстояние до цели с учетом препятствий. Эту целевую функцию надо минимизировать . Направление до цели отдельным роботам неизвестно, им доступны только измерения целевой функции в текущей точке. Также в задачу должен быть включен мультипликативный шум на уровне измеряемого сигнала.

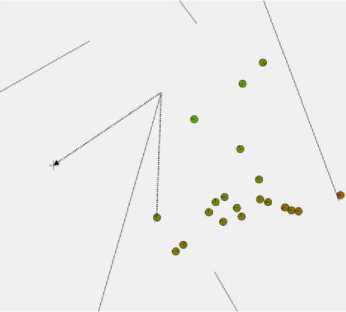
Рис. 1. Пример модельной поисковой задачи

Для каждой новой точки вычислять расстояние от нее до цели через поиск минимального пути – слишком затратно. Определим концы всех стен как опорные точки и пронумеруем их. Сперва нужно будет определить значение целевой функции для опорных точек перед началом моделирования. Затем для получения значения целевой функции для произвольной точки надо вычислить расстояние от нее до цели через все доступные в прямой видимости опорные точки:

f (X) = dist + d (X, i), где disti – расстояние до цели из опорной точки с номером i, d(X, i) – расстояние до опорной точки с номером i из точки X, fi(X) – расстояние до цели через опорную точку с номером i. Искомое значение целевой функции тогда будет равно f (X) = minievf (X), где V – множество номеров опорных точек, находящихся в прямой видимости. В случае, если в прямой видимости находится сама целевая точка, можно просто найти расстояние до нее без использо- вания других опорных точек. Таким образом можно вычислить значение целевой функции для любой точки с минимальными затратами.

Адаптация алгоритмов роевой оптимизации

В моделирующей системе реализованы абстрактные роботы, которые имеют следующие настраиваемые свойства:

• -    Роботы имеют форму круга радиусом равной одной единице расстояния.

• -    Максимальная дальность коммуникации 30 единиц расстояния.

• -    Максимальная скорость 0.8 единиц расстояния на одну итерацию.

• -    Роботы имеют канал связи, не проходящей через препятствия, с возможностью широковещательной передачи данных.

• -    Имеют компас, дающий угол к логическому северу, датчик произведенного смещения, датчик расстояния до препятствия впереди и соответствующий датчик для получения значения целевой функции.

Реализуемые алгоритмы имеют доступ к следующим возможностям:

• -    Возможность широковещательной и прямой передачи данных.

• -    Получение текущей скорости передвижения.

• -    Получение угла к северу.

• -    Измерение значения целевой функции.

• -    Отправка команд на передвижения.

• -    Получение произведенного смещения.

Можно предположить какие ограничения будут усложнять или делать невозможной работу алгоритмов оптимизации. Во-первых, это ограниченные возможности передвижения. Если алгоритм будет быстро и часто менять направление движения, то робот под его управлением будет попросту не успевать за ним. К тому же, алгоритм будет ограничен в скорости перемещения агентов максимальной скоростью движения роботов. Во-вторых, это возможность взаимных столкновений. Сталкиваясь друг с другом, роботы могут мешать работе алгоритма. В-третьих, это невозможность смерти, деления и телепортации роботов. И в-четвертых, это ограниченный радиус коммуникации. Робот может связаться лишь со своими непосредственными соседями в определенном радиусе. Это делает возможной ситуацию, когда один или несколько агентов могут отбиться от остального роя или образовать отдельный рой.

В моделирующей системе в настоящий момент реализованы адаптированные версии следующих четырех алгоритмов:

• 1.    метод роя частиц ( PSO ) [6];

• 2.  конкурентный метод роя ( CSO ) [7];

• 3.    алгоритм бактериального поиска ( BFOA ) [8];

• 4.    алгоритм светлячков ( FFA ) [9].

В силу своей простоты, алгоритм роя частиц практически не требует модификации. Однако, в формулу, определяющую вектор скорости перемещения на следующей итерации, была добавлена инерция, которая позволяет роботам двигаться более плавно, не замедляясь от резких и частых поворотов.

В алгоритме CSO имеется механизм выбора конкурента, для реализации которого на каждой итерации агенты должны быть разделены случайным образом на пары, однако в рассматриваемой модели отсутствуют единый управляющий центр и глобальная связь. Пусть каждый агент выбирает случайного соседа и бросает ему вызов. Если вызванный сосед уже в паре или по какой-то другой причине отказывает ему в поединке, то робот повторяет процедуру выбора конкурента, на этот раз исключая из выбора отклонившего вызов соседа. Это повторяется до тех пор, пока кто-то не примет его вызов, либо он сам не примет чей-то вызов. В случае, если не удается выбрать конкурента, робот продолжает свою работу. Аналогично предыдущему алгоритму была также изменена формула обновления вектора скорости перемещения, в которую были добавлены параметры для инерции и обучения.

В алгоритме BFOA процесс хемотаксиса реализован без изменений. Процесс репродукции реализован следующим образом: робот берет значение своей целевой функции и сравнивает его с значениями соседей. Если он окажется в худшей половине, то выбирает случайного соседа из лучшей половины и направляется на место, где тот находится. Если он окажется среди лучших, то он возвращается к процессу хемотаксиса. Таким образом симулируется смерть бактерии и деление, без необходимости в едином управляющем центре и глобальной связи. Процесс рассеяния был отброшен и не реализован.

В алгоритм светлячков были включены механизмы инерции и отталкивания, последний препятствует сближению всех роботов и образованию из них плотного кластера.

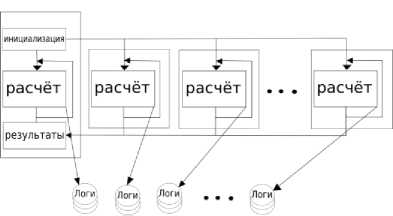
Рис. 2. Схема программы

Программная реализация

Программа моделирующей системы была реализована на языке программирования C ++ с поддержкой параллельного выполнения на основе технологий MPI и OpenMP (рис. 2). Программа принимает на вход два опциональных аргумента. Первый аргумент – путь к конфигурационному файлу; второй аргумент – строка конфигурационных параметров, которые имеют больший приоритет перед конфигурационным файлом. В конфигурационном файле указываются путь к файлу, в котором заданы препятствия, запускаемый алгоритм, параметры шумов, начальная позиция роботов, число роботов, число необходимых расчетов и пр. Сам конфигурационный файл представляет собой INI файл. После чтения параметров считывается и обрабатывается карта, в которой указываются положения всех препятствий. Далее программа распределяет равные количества расчётов по всем выделенным MPI процессам. Внутри каждого расчета алгоритм обрабатывает роботов параллельно через потоки OpenMP . По окончанию работы, программа собирает результаты и выводит их в консоль. Если включить возможность логирования в конфигурации, то на каждый расчёт создается файл с логами. Лог-файл хранит местоположение, направление, размер, значение и место лучшего найденного решения, и значение датчика дальности каждого робота на каждом итерации.

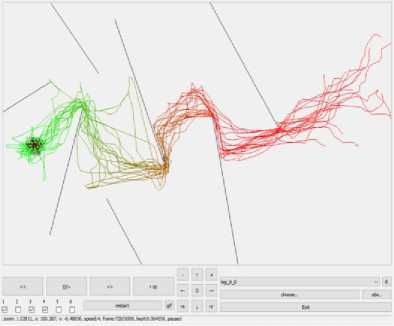
Рис. 3. Пример работы моделирующей программы

В системе реализован графический интерфейс на Qt / C ++ с возможностью визуализации работы моделирующей программы, как показано в рис. 3. Для визуализации используется лог-файл. Программа позволяет просматривать траектории движения роботов, изменять скорость воспроизведения, перемещать камеру (окно просмотра), выбирать способ визуализации роботов и создавать анимированные gif- файлы с выбранными параметрами визуализации.

Численное исследование

Для исследования сходимости алгоритмов в качестве метрики для их сравнения предлагается использовать среднее расстояние от роя до цели. Такая метрика позволяет оценить приближение к решению всем роем, а не его единичными роботами. Каждый расчёт проводился 1000 раз (по 1000 итераций). Исследование проводилось для роев из 20, 50 и 100 роботов, на карте с препятствиями и без, с шумами и без. Запуски проводились на вычислительной системе IBM Polus [10]. Использовался компилятор Spectrum MPI версии 10.1.0, которая использует IBM XL C / C ++ for Linux , V 13.1.6. Из сторонних библиотек использовался inih для чтения конфигурационных файлов.

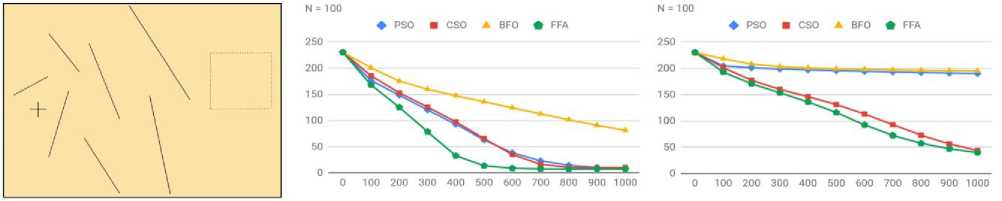
Рис. 4. Карта модели и сходимость алгоритмов без шумов (слева) и с шумом 5% (справа)

На рис. 4 слева показан пример одной из карт препятствий, использовавшихся в численных экспериментах. Справа показаны результаты сравнения эффективности четырех рассмотренных алгоритмов без шума и с шумом 5% при измерении целевой функции. Видно, что лучшим является светлячковый алгоритм. А наиболее устойчивые к зашумленности входного сигнала оказались светлячковый алгоритм и алгоритм конкурентного роя.

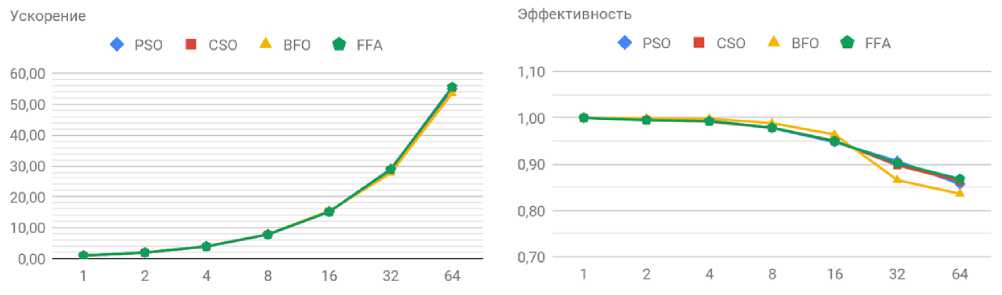
Рис. 5. Эффективность параллельной реализации системы

Также было проведено исследование эффективности параллельной реализации разработанной программной системы. Измерения производились на системе IBM Polus . Для сравнения использовался карта препятствий из рис. 4, а число расчетов было выбрано равным 128. Результаты были усреднены по 10 запускам. Запуски производились с использованием 1, 2, 4, 8, 16, 32 и 64 процессов. Из результатов, показанных на рис. 5 видно, что ускорение по процессам оказывается почти линейным. Благодаря тому, что каждый расчёт является независимым друг от друга, между процессами практически не происходит взаимодействия во время работы. Общение между процессами происходит лишь в начале и в конце работы программы. Вычислительная сложность метода роя частиц, конкурентного метода роя и алгоритма светлячков оказывается примерно одинаковой, а алгоритм бактериального поиска оказался намного легче в плане требуемого объема вычислений.

Заключение

В результате выполненной работы получены следующие результаты:

• -    была формализована модельная поисковая задача.

• -    были выбраны и адаптированы 4 алгоритма роевой оптимизации: метод роя частиц, конкурентный метод роя, алгоритм бактериального поиска и алгоритм светлячков.

• -    реализованы моделирующая система (с возможностью параллельного выполнения расчетов) и пользовательский интерфейс для визуализации ее работы.

• -    проведено численное исследование и сравнение эффективности работы адаптированных алгоритмов при разных конфигурациях препятствий, шумов и числа роботов в рое.

Из рассмотренных четырёх алгоритмов свою применимость в данной задаче лучшие результаты показали конкурентный метод роя и алгоритм светлячков. Были выявлены слабости всех рассмотренных алгоритмов. BFOА показывает сильную чувствительность к шумам в виде сильного замедления работы, однако алгоритм не расходится и всегда стремится к целевой точке. PSO работает хорошо, но только при слабых шумах или при их отсутствии. Свойство роя двигаться плотной группой под управлением метода роя частиц замедляет работу алгоритма, когда роботы теряют согласованность движения из-за влияния шумов. FFA показал себя быстрейшим, однако роботы под его управлением имеют свойство иногда отбиваться от роя, особенно при наличии шумов. Этот недостаток нивелируется увеличением числа роботов, и в случае достаточно большого роя этот алгоритм оказывается лучшим. CSO показывает хорошую устойчивость к шумам и работает хорошо даже при небольшом числе роботов. Хотя он и не имеет явных слабых мест, но работает он немного медленнее, чем алгоритм светлячков. В будущем планируется предпринять дальнейшие попытки модификации алгоритмов для устранения выявленных недостатков, а также рассмотреть другие алгоритмы данного класса.

Работа выполнена при финансовой поддержке РФФИ (грант № 17-07-01562 А).