Adaptation of Induced Fuzzy Cognitive Maps to the Problems Faced by the Power Loom Workers

Study of fuzzy theory in the context of application to the real world problems has become an important one. Still all the techniques used in the statistical analysis of any real data have no capacity to give any form of weightage to the feelings (or) attributes which ought to be associated with the problem in order to get a true situation or understanding of these problems. More so is the case in this study of power loom workers problems.

The Indian textile industry contributes twenty percent of industrial production, nine percent of excise collections, eighteen percent of employment in the industrial sector, nearly twenty percent to the country’s total export earning and four percent to the Gross Domestic Product.

There are more displacement of textile workers in Power looms factory than in Sizing factory and processing factories. Power looms workers are getting wages that many workers have migrated from one place to another place. The workers were facing financial, health, housing, and social, educational and on piece rate system, they have not getting any facilities. To overcome to these problems many workers shifted to their native places. It is in this context the study attempts to examine the socio-economic problems faced by the power loom workers

The strategies of globalization and the subsequent restructuring of economies, including the increased mechanization of labor has had stifling effects on the lives of the Power loom Workers in Avinashi, in Tamil Nadu in India.

This paper has four sections. Introductory part is given in section one. In section two we recall the definition of fuzzy Cognitive Maps, Induced Fuzzy Cognitive Maps and its Properties .Section three is devoted to the adaptation of the Induced Fuzzy cognitive Maps to the Power loom workers. In section four we give the conclusions based on our study.

• II.    FCMS And Induced FCMS

• 2.1    Basic Notions of Fuzzy Cognitive Maps

  Fuzzy Cognitive Maps are techniques that attempt to depict and analyze the cognitive process of human thinking and human behavior on specific domains by creating models. These models are represented as signed directed graphs of concepts and by the various casual relationships that exists between the concepts. In 1976 Axelrod[1] proposed cognitive maps as a formal tool for decision-making. He used the matrix representation of the directed graph to represent and

  study the social scientific knowledge. In 1986 Kosko[2] proposed FCMs based on the cognitive maps structure.

In this section we recall the notion of Fuzzy Cognitive Maps (FCMs), which was introduced by Bart Kosco[2] in the year 1986. FCMs have a major role to play mainly when the data concerned is an unsupervised one. Further this method is most simple and an effective one as it can analyze the data by directed graphs and connection matrices.

Definition2.1.1

An FCM is a directed graph with concepts like policies, events etc. as nodes and causalities as edges. It represents causal relationship between concepts.

If increase (or decrease) in one concept, leads to increase (or decrease) in another, then give the value 1. If there exists no relation between two concepts, then the value 0 is given. If increase (or decrease) in one causalities decreases (or increases) another, then give the value –1. Thus FCMs are described in this way.

Definition 2.1.2

When the nodes of the FCM are fuzzy sets then they are called as fuzzy nodes.

Definition 2.1.3

FCMs with edge weights or causalities from the set {–1, 0, 1}, are called simple FCMs.

Definition 2.1.4

Consider the nodes or concepts C 1 , …, C n of the FCM. Suppose the directed graph is drawn using edge weight e ij e {0, 1, -1}. The matrix E be defined by E = (e ij ), where e ij is the weight of the directed edge C i C j . E is called the adjacency matrix of the FCM, also known as the connection matrix of the FCM.

It is important to note that all matrices associated with an FCM are always square matrices with diagonal entries as zero.

Definition 2.1.5

Let C 1 , C 2 , …, C n be the nodes of an FCM. A = (a 1 , a₂, ..., a n ), where a i ^e {0, 1}. A is called the instantaneous state vector and it denotes the on-off position of the node at an instant.

'0 if a1 is OFF

1 if ai is ON ,where i = 1,2,...,n

Definition 2.1.6

Let C 1 , C 2 , … , C n be the nodes of an FCM. Let

C 1 C 2   C 2 C 3

C i C j …,

be the edges of the

FCM (i ≠ j). Then, the edges form a directed cycle. An FCM is said to be cyclic if it possesses a directed cycle. An FCM is said to be acyclic if it does not possess any directed cycle.

Definition 2.1.7

An FCM with cycles is said to have a feedback.

Definition 2.1.8

When there is a feedback in an FCM, i.e., when the causal relations flow through a cycle in a revolutionary way, the FCM is called a dynamical system.

Definition 2.1.9

CC C C    CiCj

Let 1  2 ,   2  3 , …,      j be a cycle. When Ci is switched ON and if the causality flows through the edges of a cycle and if it again causes Ci, we say that the dynamical system goes round and round. This is true for any node Ci, for i = 1, 2, … , n. The equilibrium state for this dynamical system is called the hidden pattern.

Definition 2.1.10

If the equilibrium state of a dynamical system is a unique state vector, then it is called a fixed point.

Example

Consider a FCM with C₁, C₂, …, C_n as nodes. For example, let us start the dynamical system by switching ON C 1 . Let us assume that the FCM settles down with C1 and Cn ON that is, the state vector remains as (1, 0, 0, …, 0, 1). This state vector (1, 0, 0, …, 0, 1) is called the fixed point.

Definition 2.1.11

If the FCM settles down with a state vector repeating in the form A 1 → A 2 → … → A i … → A 1 , then this equilibrium is called a limit cycle.

Definition 2.1.12

We denote the combined FCM adjacency matrix by E=E1+E2+… +Ep.

Finite number of FCMs can be combined together to produce the joint effect of all the FCMs. Let E 1 , E 2 , … , E p be adjacency matrices of the FCMs with nodes C 1 , C 2 , …, C n , then the combined FCM is got by adding all the adjacency matrices E 1 , …, E p .

Notation

Suppose A=(a₁, …, a_n) is a vector which is passed a ′ , ..., a ′ into a dynamical system E. Then AE = (  ^{1        n} ).

After thresholding and updating the vector suppose we

a′       a′ get (b1, ..., bn), we denote that by (  1’    , n)^(b1, b2, ..., bn). Thus, the symbol ‘^’ means the resultant vector has been threshold and updated.

• 2.2    Algorithmic Approach in Induced Fuzzy Cognitive Maps(IFCMs)

Even though IFCM is an advancement of FCM it follows the foundation of FCM, it has a slight modification only in Algorithmic approaches. To derive an optimistic solution to the problem with an unsupervised data, the following steps to be followed:

Step 1: For the given model (problem), collect the unsupervised data that is in determinant factors called nodes.

Step 2: According to the expert opinion, draw the directed graph.

Step 3: Obtain the connection matrix, M, from the directed graph (FCM). Here the number of rows in the given matrix = number of steps to be performed.

Step 4: Consider the state vector C 1 which is in ON position. Find C 1 ×M.

The state vector is updated and threshold at each stage.

Step 5: Threshold value is calculated by assigning 1 for the values > 1 and 0 for the values < 0. The symbol ‘ ^ ’ represents the threshold value for the product of the result.

Step 6: Now each component in the C 1 vector is taken separately and product of the given matrix is calculated. The vector which has maximum number of one’s is found. The vector with maximum number of one’s which occurs first is considered as C₂.

Step 7: When the same threshold value occurs twice. The value is considered as the fixed point. The iteration gets terminated.

• III.    Adaptation of Induced FCMS to the Problems Faced by the Power Loom Workers in Avinashi in Tamilnadu, India

Now we illustrate the dynamical system by a very simple model from the problem of power loom workers. At the first stage we have taken the following seven arbitrary attributes (S 1 , S 2 ,  , S 7 ). It is not a hard and fast rule we need to consider only these nine attributes but one can increase or decrease the number of attributes according to needs. The following attributes are taken as the main nodes for study.

An expert system spells out the seven major concepts relating to the power loom workers as:

• S 1 =    Illiteracy

• S 2 =    Poor salary

• S 3 =    Bad habits

• S₄ =    Lack of medical centres

• S₅ =    Lack of nutrients

• S 6 =    Poverty

• S 7 =    Cut-Off electricity power.

• 3.1    The Directed Graph Related to the Power Loom Workers

  

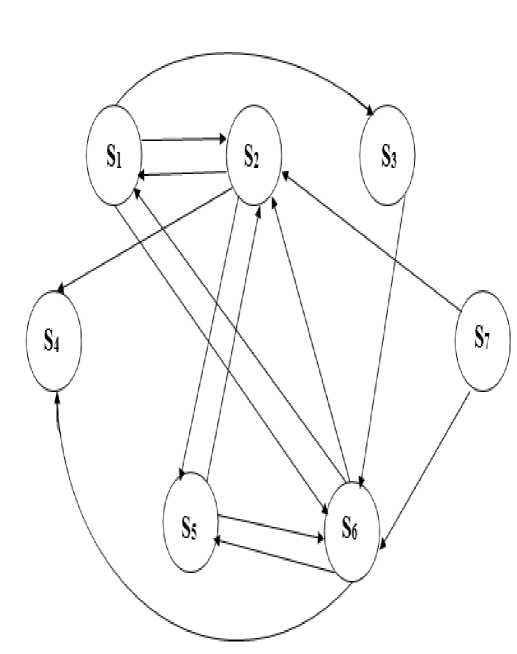
  Figure 3.1: Directed Graph

  
  

• 3.2    Implementation of IFCMs Model to the Study

Based on the expert’s opinion, the directed diagram is drawn and the corresponding connection matrix M is given as

S1		S2	S3	S4	S5	S6	S7
S1	0	1	1	0	0	1	0
S2	1	0	0	1	1	1	0
S M = 3 S4	0	0	0	0	0	1	0
	0	0	0	0	0	0	0
S5	0	1	0	0	0	0	0
S6	1	0	0	1	1	0	0
S7	0	1	0	0	0	1	0

Now using the matrix M we determined the problems. Let us start Illiteracy is taken as the ON state and all the other nodes are in the OFF state.

(i.e) C 1 = (1 0 0 0 0 0 0)

Product of C1 and M is calculated.

C 1 M = (0 1 1 0 0 1 0)

~ ( 1 1 1 0 0 1 0 )

= C 1¹

Threshold value is calculated by assigning 1 for the values >1 and 0 for the values <0. The symbol ‘^’ represents the threshold value for the product of the result.

Now as per Induced Fuzzy Cognitive Map methodology, each component in the C 1 ¹ vector is taken separately and product of the given matrix is calculated. The vector which has the maximum number of one’s which occurs first is considered as C_2.

The symbol ~ denotes the calculation performed with the respective vector, here C 1 ^1.

C 11 x M ~ (1 0 0 0 0 0 0 )x M	When the same threshold value occurs twice, the value is considered as the fixed point. The iteration gets
→ (0 1 1 0 0 1 0)	terminated and the calculation gets terminated.
C 11 x M ~ (0 1 0 0 0 0 0) x M	Likewise any state vector can be taken and its effect can be analyzed.
→ (1 0 0 1 1 1 0)
C 11 x M ~ (0 0 1 0 0 0 0 ) x M	IV. Conclusion
→ (0 0 0 0 0 1 0) C 11 x M ~ (0 0 0 0 0 1 0) x M	In this Section we have summarize the major findings in section three using IFCMs and interviews data.
	•    While analyzing with IFCMs, we observe that
→ (1 0 0 1 1 0 0) Therefore C 2 = (1 0 0 1 1 1 0)	when Illiteracy is taken as the ON state, the resultant vector is (1 0 0 1 1 1 0 ).
	•    While analyzing with IFCMs we observe that
C 2 x M = (1 2 1 1 1 1 0)	Illiteracy, Lack of medical centers, Lack of nutrients, Poverty are the major problems to the
Product of C 2 and M is calculated.	power loom workers.
~ (1 1 1 1 1 1 0)	•    The Cut-off electricity power is also one of the
	problems to the power loom workers.
= C 21	•    The Government should take steps to these
C 21 =(1 1 1 1 1 1 0)	problems.
C 21 x M = (1 0 0 0 0 0 0) x M	FCMs have several advantages as well as some
→ (0 1 1 0 0 1 0)	disadvantages. The main advantage of this method is simple. It functions on expert’s opinion. When the data
C 21 x M = (0 1 0 0 0 0 0) x M	happens to be an unsupervised one the FCM comes handy. This is the only known fuzzy technique that
→ (1 0 0 1 1 1 0)	gives the hidden pattern of the situation.
C 21 x M = (0 0 1 0 0 0 0) x M	Although this research is unique, it has a couple of limitations also. First, the limitation of IFCM. This
→ (0 0 0 0 0 1 0)	model consists of lengthy procedure for calculation which is not suitable for calculation with the matrices
C 21 x M = (0 0 0 1 0 0 0) x M	which has higher number of rows and columns. Second, this manual calculation is fully based on the Expert’s
→ (0 0 0 0 0 0 0)	openion. So, it may lead to personal bias. But to deal with an unsupervised data, the IFCM model predicates
C 21 x M=(0 0 0 0 1 0 0) x M	the accurate results when comparing with FCM model.
→ (0 1 0 0 0 0 0)
C 21 x M = (0 0 0 0 0 1 0) x M	Acknowledgment
→ (1 0 0 1 1 0 0)	The authors would like to heartily thank the anonymous reviewers for their careful reading of this
Therefore  C 3   = (1 0 0 1 1 1 0)	paper and for their helpful comments.
= C 2.
The fixed point is C3 = (1 0 0 1 1 1 0).