Adaptive Cross-layer Resource Allocation by HNN in OFDM-MISO System

Paper[6] proposed a novel algorithm, and used greedy algorithm to solve the problem, but the greedy algorithm is a local sub-optimal algorithm without taking into account the overall various possible situations. The objective of cross-layer formulation[7] is to allow joint determination of power control, frequency-selective OFDM scheduling and multi-hop routing in order to maximize the minimum throughput, but their approach was based on water-filling method which is very complex, thus not practical. In paper[8], HNN has been proven to be successful in solving dynamic resources allocation problems in a short time, but the crosslayer optimization was not taken into account. According to optimal or sub-optimal system capacity schemes, authors[9] proposed intelligent algorithm selected a user combination for a fixed number of users within few generation iterations, but it did not combine OFDM and Multiple-Input Single-Output (MISO) as one system leading to the question too simple.

From above, we propose the HNN and GA methods for the problem which is cross-layer resource allocation optimization problem with the fairness in multi-user OFDM-MISO System.

• 2.    Model and Analysis

First, Assume that a system with a base station equipped with N _T antennas and K mobile users, and each user equipped with one antenna is receiving signals from the base station. Considering information bits allocated on the m th sub-carrier from the K users are first encoded to produce the encoded symbols as U j,'", U_mл^ .The encoded symbols are assumed to have unit variance and are amplified by the respective power gains as ^1 ,...,^^ p _m , _k □ 0 and carried by the П т □ 1 spatial multiplexing weight vectors as ^ w _{m 4},-,w _m , к^ , respectively. The processed signals are fed to the m th inputs in the bank of n _T Inverse-Discrete-Fourier-Transform (IDFT) processors, and the n_T □ n_f outputs of the IDFT are first added with cyclic prefix. The resulting n_Tn_f □ n^ _Ucr b blocks of time-domain samples are transmitted over the n _T transmit antennas column by column. At the receiver of each of the mobile users, there is a corresponding DFT block. So at the m th input of the IDFT block, the n _T □ 1 transmitted signal B m is given by B _m □ □ .nT w _mk m , _k . Without loss of generality, k 1

the П т □ 1 frequency-domain received signal vector of the k th mobile user is given by Y _k □ H _k B □ Z _k , where B is the n_Tn_f □ 1 aggregate transmit vector at the input of IDFT, given by _Bn □ B ⁰ □ , H_k is the n_f □ n_fn_T block □      □

• □ ^B nf -¹ □

• □ H o. k 00 □

diagonal channel matrix aggregated over the П. sub-carriers of user k, given by „  □ n        □, where nm, f                                                             H k □ □ 0          0 □                    ,

• □    о о н □

• □                        nf -1, ^k □

denotes the i n n _T channel matrix between the n _T transmit antennas and the k th mobile user in frequency domain and Z _k presents the n_f □ 1 zero-mean white Gaussian noise with covariance matrix . 2_z .

Hence, considering m th sub-carrier allocated on the k th mobile user, the received signal is given by

Y J H _tB □ Z _t m , k m , k m m , k

（ 1 ）

In the OFDM-MISO system, sub-carriers can be allocated on a user depending on the instantaneous channelstate-information (CSI). So the cross layer scheduling algorithm can be cast into the following optimization problem. Choose the user’s set allocation a_a_; ,•••, A^ and the power allocation P n ^ P_m,:m m n n 0, n_f в 1g, k n A ^ according to the given CSI realization H 1 , , H K , under the conditions of n f 1

n n Pm,k n P0 and |Am| n nT for all mn n0,nf n 1n. Assume that the total transmission power from the base station m 0 k Am is constrained at P0. The objective is to optimize the maximization of the system throughput П k/к -H- , where rk is given by equation:

r_k - H k - n

n n log2 n1 n n m:k=Am      n

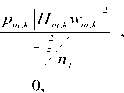
otherwise

m

（2）

• 4.    Steps of Cross-layer Design Algorithm

There are two sets of optimization variables: the active user allocation A and the power allocation P . The former is a discrete variable and the latter is a continuous variable. In our approach algorithm, the sub-carrier with the highest channel gain among the available sub-carriers should be allocated to a node to achieve the best throughput performance. Therefore, the optimization problem can be solved in the following steps.

Step 1: Initialization. For each sub-carrier m n n 0, n_f n 1 n , initialize the active user sets A _m such that |A _m | n n _T .

Step 2: Optimization with respect to A . Let - - 1 ,", - _k - be a discrete decision variable to represent A . If subcarrier n is allocated to use k , -, n 1 , otherwise -, n 0 .

k , n                       k , n

Step 3: Optimization with respect to P . Here we adopt M-QAM modulation, when adopting HNN to solve the problem, the transmit power of c bits per OFDM symbol is given as D D /3nQOn 1 n peПП 2cai , where pe is the P '     0 ПL      4      "       "

required bit-error-rate (BER), and Q-function is defined as

Q ^- * ^-B 72 7 °°

n t ² / 2 ,, e      dt

so from bit matrix c we can

calculate the power allocation P . When we adopt GA to solve the problem, given the active user sets A m , the optimization problem can be written into the following Lagrangian function:

• nf ’1     n n p H w , I          nn

  （ 3 ）

  
  

m , k     m , k m , k

^L - P m , k . < -ⁿn n ⁿ log 2 0 1 0 ----V------¹ 0 / P m , k Ш

• m -0 teA. n     □         - = / n f               Пв

where c is the Lagrange multiplier chosen to satisfy the total transmit power constraint P ₀ . With standard optimization techniques and the Karush-Kuhn-Tucker (KKT) condition, the optimal power allocation is given by

*

P m , k ⁰

D 1

0----1----0

0- ln2 „ c

- = / П/

^Hm , k ^wm , k ²

D

D

D

（4）

• 5.    Optimization Using the GA Method

The main optimization steps with GA for the problem are described as follows:

• (1) .Coding: Basic features of genetic algorithm are that they work on coding space and solution space alternatively.

• (2) .Crossover: Crossover Operates on two chromosomes at a time and generates offspring by combining both chromosomes’ features. For two chromosomes chosen with crossover possibility ^p c , we use arithmetical crossover operators.

• (3) .Fitness function: The particular chromosome can be ranked against all the other chromosomes. fitness function is defined in (2).

• (4) .Mutation: For each chromosome chosen with mutation probability p _m , the method replaces each element with a random value.

• (5) .Optimization process:

• 6.    Optimization Using the HNN Method

• 6.    1 User set allocation

Step1 : Initialize population. Each element in the chromosome is a power allocated to sub-carriers, thus, population is a 2-D array, where the rows represent chromosome numbers and columns of a row represent subcarriers.

Step2 : Evaluate the individual values in population using fitness function.

Step3 : Generate the new population using crossover and mutation probability.

Step4 : Repeat step2 and step3 till the algorithm converges.

The optimization problem is reformulated as:

" K ,   ° pH , k W m , k f n

R °D П - m,k log2 °1 °        

（ 5 ）

m=1 k=1             °         ■ z1 nf°

Subject to ：

• (i)    1 °  °          , n ° ^ 1,2, •••, N ^ , it denotes that the sub-carrier is allocated on each user.

k ° 1

(ii)

N

n, °

k

n °

_T k , n

it denotes the fairness constraint

• (iii)    N °  □   □        , it denotes each sub-carrier is allocated.

. ,     . k, n n ° 1 k ° 1

• (iv)    R. : R ° t : t , it denotes the initial rate of each node constraint.

For the sub-carrier allocation, the energy function proposed by HNN is:

M K          ° p\h w |2 ° n M n K

E D Max D A □□ „ , , , log , ° 1 D ¹  *‘ * ^, k¹ °0- Q_D° ^- , , , D 1 _D D

（ 6 ）

m= 1 k=1              °         - z / nf °    2 *=1D k=1

K M         2     KM         2    K M

• -□ °D -mt° n° ° D°D □ -mt°M° ° -□ °D Rt° nLR° °      m, k     k °        °           m, k       °            °      *, k°

• k=1 ° m=1            °     2 ° k=1 m=1             °     2 k=1 ° m=1

The dynamic equation of the HNN method can be calculated as:

• 0 dUk,n aпц    log ni□ PHAkLппп вОц

  （ 7 ）

  
  

m, k     22                                                 ।।m, k।। dt        0 k            _       - z /nf    __     □ k_

• _             _               □               f□_

• □□   □               □     □                   □        □            nk

• □ C 00 - m, k 0 nk 00 D 00 □ - m, k 0 M 00 F □ 00 Rk, m 0 TT

• _  _ m         _    _ km         _    k _ m

• 0 Vm □ g - Uk,m -0 1 01 □ th □00

• □                   2 _      _ U0

• 6.    2 Bit-loading

From above, we structure the HNN for solving the user set allocation. By the networks， from the initial stateU , after the continuously iterated by the dynamic equation of the networks, we obtain the output of the networks which is the user set allocation matrix ρ .

In order to solve the problem, we divide bit matrix c into three matrixes: sub-carrier allocation matrix ρ , HNN output matrix v , v^ . _ j ),^ for all n , j , and bit allocation matrix l whose elements are denoted the number

•••, M ^. We give the method of calculating c as follows:

of bits allocated on the every sub-carrier, l ^ _ ^0,1,

• 1)    The elements of matrix v are multiplied by the corresponding of the matrix l , then get matrix npn ;

• 2)    Matrix npn is multiplied by matrix kpn     whose elements are all 1s, then get matrix mpn .

  - i _ j ,

• 3)    Extending matrix mpn to k lines, get matrix lpn , and then the elements of matrix lpn are multiplied by the corresponding of the matrix ρ , at last we get matrix c .

The optimization problem is formulated as:

MK

R 0 0 0 - m,k

_ log 2 ^{_ 1} □

_

T - 2^     □ 1 , H m , k W m , k |² _

- d n,         _ f               _

（ 8 ）

where t _ N". _ q- ¹ _ peL __

3 _-Z--    □     □_

_    _ 4 __

For the bit-loading, the energy function proposed by the HNN method is ：

MK

E □ MAX _ A _ _ - m 1 k 1

log₂ ⁰ 1 0

² 0

T _r2 ^m j n14 H mk W mk f - z / П/

^S n □ n ,^D T □ □ □ v m , j ^_ 10 □ ² m-. 1 _ j =1            _

KM

D 0 □ _ R km 0 n y R ² k =1 0 m =1         ^M

C 0 M 2

-0 0 0 v m , j '^{0 M} 0 ⁰

（ 9 ）

2 0 m=1 j =1

02 F 0 nn      D0

0 ⁰  -0 0 0 P m,k ⁰ P total 0

0       2 0 n=1 j =1

• □    dUm ,

• □ mj

• □    dt

n

D

• □    B □□,

• □  □ j

□    A □

k

——

_{T 2} m , kvm , jlm , j _{H   w}

zV n f □ T „ 2 ^ -v-j'-j ^ 1 „ \H„ , - w m,- f

D        m         D

V m , j □ ! □□ C □ □ □ V m , j □ M □□

• □     □ m j

п

• □    D □ □ □ R -m □ n^R □ □ F □ □ □ P m- □ P„ a □

• □    k □ m- 1       M □    □ km           □

• □    V mj □ g ^ U mj . □ |a1 □ th □ U mj □□

• □                    ² □      □ ^U 0 □ □

• 7.    Parameter Setting and Simulation Result

（10）

From above we structure the HNN to solve the bit allocation and obtain the HNN output matrix v then get bit-loading matrix c .

In order to ensure E □ 0 , we add a constant MAX, constants A, B, C, D, and F are the weigh terms of the energy function and the dynamic equation, and their values are selected to obtain a fast convergence of the desired solution.

We do simulation in OFDM/MISO system with 10 transmitting antennas, 10 mobile users, modulation is 64-QAM. The wireless channel is modeled as a frequency-selective channel consisting of 12 independent Rayleigh-multipaths. White noise . _z² □ 10 4 ; Bit error rate ber □ 10- 4 . HNN’ parameters setting: A =100, B =500, C =50, D =10, F =10;

HNN-32

GA-32

Rbest-32

GA-16

HNN-16

Rbest-16

2      3     4      5      6      7      8      9     10    11     12

Total transmission power

Figure 1.Performance comparison of the throughputs

HNN neurons slope is U =0.02, HNN calculation step is 0.0001, the times of iteration is 2000. The parameters of GA for the problem are provided below:

We choose the linear structure coding method, through which a chromosome presents a feasible solution of the power allocation; Population size = 20; Terminal generation number = 100; Crossover probability = 0.6; Mutation probability = 0.1.

Fig.1 plots the throughputs respectively when the number of sub-carriers is 16 or 32. HNN-16, HNN-32 denoted the throughputs when the number of sub-carriers is 16 or 32 adopted by HNN algorithm under the different transmit power constraints; GA-16, GA-32 denoted the throughputs adopted by GA algorithm; and

Rbest-16, Rbest-32 denoted the throughputs when it did not take into account the multi-users option. As is known, in OFDM system as the users’ number increase, the increase of system diversity gain can lead to the increase of system throughput, which is consistent with the simulation results, as shown in Fig.1. Clearly, the general effectiveness based on HNN and GA algorithm is superior to that adopted by Rbest’s algorithm[10], because system resources can be more reasonable distribution after the multi-users selection. HNN and GA algorithm can effectively solve the problem as a global optimization algorithm, but the effect of the former is better than that of the latter when the number of sub-carrier is 32 as shown in the figure, which indicates that HNN algorithm is more suitable to solve this problem in large-scale systems. However, with the increase of users’ number, the number of system’s local sub-optimal solutions sharply increases, which leading to performance degradation of HNN and GA.

Generally, the values of parameters A, B, C, D, F range from 0 to 1000, and their values are not the same when we solve different problems; But their values have a major impact on the effectiveness and level of the network convergence; After several simulations, we obtain that parameters’ values are inversely proportional to the convergence value of the corresponding items in dynamic equations.

• 8.    Conclusion

In this paper, we propose the HNN and GA methods for the problem which is cross-layer resource allocation optimization problem with the fairness in multi-user OFDM-MISO system. At the same time we divide the bitloading matrix into three matrixes, which can simplify the problem in such system. Our approach is to decompose the problem into two steps: user set allocation and bit-loading, by taking HNN’s and GA’s advantages of the inherent parallelism, a real-time running and its global optimum. The simulation results show that our proposed methods by HNN and GA can effectively solve optimization problems in OFDM-MISO system, and the general effectiveness based on HNN is superior to that adopted by GA and traditional methods.

Acknowledgment

This work is supported by the Natural Science Foundation of Shandong Province (No. ZR2010FM040 ).