Adaptive finite-time convergence fuzzy ARX-laguerre system estimation

Published Online May 2019 in MECS

Robotics has become a critical area for industries and academic communities in recent years. Various types of robots have been introduced by robotics research centers around the world. One of the essential industrial applications of robots is robot manipulators. Industrial robot manipulators have been extensively used in two parallel areas: industries and academic applications [1]. These types of robots have three main challenges: modeling, control, and fault diagnosis. The main issue concerning robot manipulators is dynamic behaviors. Such systems are highly nonlinear; the variation of time and coupling are affected between joints and links. Because of these issues, modeling, control, and diagnosis of faults in these systems are significant problems. Newton-Euler (NE) system modeling is one of the critical forward and backward system modeling methods for robot manipulators. Based on the literature [2], various researchers have been using this method for robot modeling and design model-reference controller/fault identification. Despite various advantages of the NE method, accuracy and unknown parameters are two main drawbacks of this technique.

To address these drawbacks, the least square [3] method was introduced to identify unknown parameters in robot manipulators. Various other techniques focus on successful access to identify the unknown parameters, but few consider fast convergence. Fast convergence has played an essential role in accurate modeling of the uncertainties [4].

The first vital part for system analyses is system modeling and estimation. In recent years, system estimation for  linear and nonlinear  systems have expanded significantly. Different techniques for system estimation have been introduced, such as linear and nonlinear system techniques. Linear system estimation (ARX, ARMAX, AR, etc.) has been used in many applications, but for accurate estimation in the presence of noise and uncertainties, these techniques have various problems. To improve the performance of linear estimation techniques, nonlinear techniques for system estimation have been introduced in the literature [5]. Nonlinear estimation techniques can be divided into three main categories. The first nonlinear identification technique is a mathematical parameter identification technique, such as the ARX-Laguerre method. This technique has been used in different systems for estimation, such as bearing and distillation columns [6, 7]. The second type of nonlinear system identification method is intelligent techniques, such as fuzzy logic, neural network, and intelligent adaptive techniques. These techniques have been used in various applications, such as robotics and rotation machinery [8, 9]. The third technique for system identification is the hybrid method. The ARX-intelligent technique and ARX-Laguerre intelligent method are two essential methods included in hybrid system estimation techniques.

In this paper, we developed an adaptive fuzzy method to estimate and model robot manipulator parameters. Inverse dynamic modeling and fast convergence challenges are solved via application of a robust adaptive technique in the fuzzy logic algorithm. Therefore, the main contributions of this research paper are as follows:

• 1)    A robot manipulator is modeled with the minimum error based on the fuzzy logic algorithm.

• 2)    An adaptive technique is used to improve the robustness and increase the convergence speed.

This paper has the following sections. Related work will be presented in Section 2. The paper challenge and proposed method objectives will be presented in Section 3. Section 4 provides the proposed method. The results and discussion will be presented in Section 5. Section 6 concludes this paper.

The application of artificial intelligence in system identification and system estimation is proposed in [14]. In that research, the system is modelled by the system’s data using the neural network technique. The adaptive network-based fuzzy inference system (ANFIS) system estimation technique is proposed in [15]. Based on [15, 16], the neural network method improves the performance of derivative techniques, heuristic methods, and hybrid techniques.

NOMENCLATURE

Γ	Torque
R N	Inertia matrix
R Θ	Nonlinear term
R Ω	Gravity
R Ψ ( q , q )	Uncertain and unknown parameter
R Φ ( q )	Coriolis force
R X ( q )	Centrifugal force
ϖ	Bounding function
R ˆ Ψ ( q , q )	Dynamic model of uncertainty
Δ R Ψ ( q , q )	Bounded uncertainty
I	Identity matrix
em , m	Fuzzy inputs
σ m	Fuzzy outputs
mmm H Γ , He , f	Fuzzy sets
µ H , f	Fuzzy set membership function
δ m	Firing strength part
µ H , f	Non-fuzzy membership definition
∂ ( x )	Adaptive learning function
x , y	Tuning parameters in fuzzy modeling
e	Performance index

• III.    Problem of Robot Inverse Dynamic Modeling

Modeling the dynamics of the system has been used for many applications, such as system behavior understanding and design model-based control algorithms. For robot manipulators to design motion controllers, accurate modeling of the robot manipulator can play an important role. For robot manipulator modeling, we have two essential options: mathematical modeling from the system’s physics and system identification modeling. Regarding the literature [10], the dynamic behavior of the robot manipulator is entirely nonlinear. Based on the NE theory, the general form of the dynamic formulation of the robot manipulator is written as the following equation:

Γ=RN(q)[q]+Rθ(q,q)+RΩ(q)+RΨ(q,q)(1)

Based on [10], the nonlinear effect of the robot manipulator parameters can be defined as follows:

Rθ(q,q)=RΦ(q)[q q]+RX(q)[q]2(2)

In the robot manipulator, the unknown and uncertain parameters can be defined as the following:

RΨ(q,q)=ΔRΦ(q)[q q]+ΔRΧ(q)[q]2 +ΔRΩ(q)

II. Related Work

Modeling of industrial systems such as robot manipulators has an important role in designing modelreference controllers and model-reference fault indicators. Tischler [11] introduced various system identification techniques to control aircraft. A review of various techniques for nonlinear system identification methods is proposed in [12]. In this research, the authors compared seven different system estimation methods, namely: (a) linearization, (b) the time domain method, (c) frequency domain techniques, (d) the time-frequency domain technique, (e) the modal method, (f) the block-box technique, and (g) the numerical model updating method. Based on [12], the numerical model updating method based on the Bayesian method increases the performance in uncertain systems. The application of system modeling and estimation of the system’s dynamic behavior in fault detection and identification (FDI) has been proposed in [13]. In [13], canonical variable analysis is introduced for system estimation, fault detection, and fault identification.

To model the robot manipulator based on the mathematical (physical) algorithm, (1), (2), and (3), the actual angular/prismatic position of the robot manipulator is represented as (4):

∫∫ [ q ] = ∫∫ R N ( q ) ^{- 1}× ( Γ- R Θ ( q , q ))

+ R _Ψ ( q , q )

R Θ ( q , q ) = R Φ ( q )[ q q ] + R Χ ( q )[ q ] ²+ R Ω ( q )         (5)

R _Ψ ( q , q ) = R _N ^{- 1}( q )( Δ R _Φ ( q )[ q q ] +

Δ R Χ ( q )[ q ]² +Δ R Ω ( q ))

According to (3) and (4), the main challenge for mathematical modeling of the robot manipulator for control or fault identification is unknown and uncertain parameters. Based on the robot manipulator dynamic formulation, the mathematical formulation of the robot manipulator is incredibly complicated and uncertain, therefore, the task of modeling is a significant challenge.

To address this challenge, this research proposes the use of an adaptive ARX-Laguerre system estimation technique. A block diagram of the proposed method is depicted in Fig. 1.

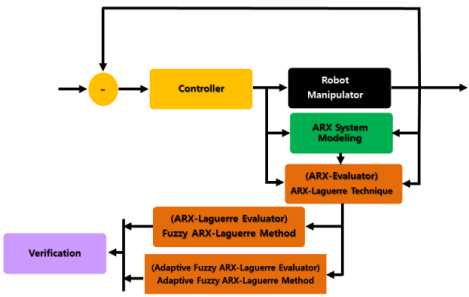
Fig.1. Block diagram of the proposed method for system modeling

The range of frequency response for a six degrees of freedom (DOF) robot manipulator is illustrated in Fig. 2. According to this figure, the resonance frequency for this system is approximately 25.5(Rad) .

sec

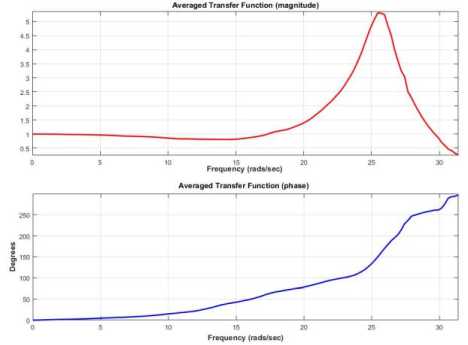
Fig.2. Robot manipulator frequency response

Based on Fig. 1, fuzzy logic is one of the critical methods for system modeling that works in unknown conditions. This technique can be used for systems that have limited mathematical definitions. To reduce the modeling error and improve the modeling accuracy, a proposed system estimation based on adaptive fuzzy algorithm is presented.

• IV.    Proposed Methodology

The proposed method is comprised of four major parts: (a) system modeling based on the ARX technique, (b) evaluation of the ARX system estimation based on the Laguerre technique and design ARX-Laguerre system estimation, (c) evaluation of the performance of the system estimation based on the flexible (fuzzy) technique, and (d) use of the adaptive technique to improve the accuracy of the system estimation performance.

It is known that uncertainty is a significant challenge for control and fault identification. Two essential methods can be used to handle uncertainties. The first one is random modeling based on probability, and the second technique is extracting equations related to the uncertainties and unknown parameters. Based on the second method, the system works in a satisfied condition, however, it has uncertain and unknown parameters. One of the main techniques to solve the uncertainties based on the second technique is the use of intelligent methods. Different techniques have been used for system modeling based on intelligent techniques, such as fuzzy logic, neural network, data-driven, and machine learning. These techniques have been used to improve the performance of the linear system estimator as a hybrid technique. The IF-THEN rules beside the membership function can be used to solve the uncertainties problem as the deterministic technique.

Based on its definition, uncertainty is divided into two main categories. The first type is structure uncertainty, which used when there are inaccuracies in the system’s dynamic parameters. Solving the challenge of structural uncertainties is significant to design a model-reference controller or fault identifier. The second type of uncertainty is unstructured uncertainty while reflecting the error in the unmodelled system’s dynamic. It is imperative to define the band of uncertainties as follows:

Δ R Φ ( q )[ q q ] +Δ R Χ ( q )[ q ]² +Δ R Ω ( q ) ≤ ϖ (7)

Based on (7), if we do not have any information about uncertainties or the bounding function, this type of uncertainty is introduced as unstructured uncertainty. Therefore, the central concept has defined a function for estimation of the system uncertainty.

The next challenge to define the effect of uncertainty is dynamic system uncertainty. When the system’s uncertainty is changed over time (frequency), modeling the uncertainties in this condition is challenging and includes the dynamics of the sensor, system resonance, and noise, which is measured by sensors. In this condition, the adaptive method is recommended to solve the challenge of dynamic uncertainties. The adaptive technique is used to design a robust estimator for dynamic modeling of the robot manipulator. Two techniques can be defined as the uncertainties: the additive method and multiplicative technique, which is defined as follows. Regarding (8) and (9), both techniques are suitable to describe the structure and unstructured uncertainties.

R _Ψ ( q , q ) = R ^ˆ _Ψ ( q , q ) +Δ R _Ψ ( q , q )

→ R _Ψ ( q , q ) - R _Ψ ( q , q ) = Δ R _Ψ ( q , q ) ≤ ϖ

Based on these two equations, two types of uncertainties are lumped into (8) or (9), which caused an increase of modeling accuracy and simplified the design model-reference controller or fault identifier.

R ^ ( q , q) = R у ( q , q )( I + A R _T ( q , q ))

^ | R ^ ⁽ q , q ) ^{- R} ^ ⁽ q , q )|| = ||^{A R} ^ ⁽ q , q ) ^R ^ ⁽ q , q )||

<||^{A R} _T ⁽ q, q )|||| ^R _T ( q, q )||                                   ⁽⁹⁾

>< g|| ^R _T ( q, q )||

Based on the ARX-Laguerre function, (15), the polynomial function is proposed in (16) and (17) .

Based on Fig. 1, the first step to system modeling in this research is the ARX method. This technique is a powerful system identification methods. The ARX technique is defined as the following expressions:

n

д(к) = д0 +Ldiii^iii (к) + и =1

nn

LL^d «л ^д Ai^(к) A i^ ^{(к) +} ...

zz ‘1 = 1 И = 1

The coefficient in the

function is represented as

ARX-Laguerre polynomial

д ( к ) + 1^( к - 1) + 2 ₂ к^к — 2) + ... + w д ( к - n _q ) = a 1 q ( к - 1) + a ₂ q ( к - 2) + ... + a i q ( к - n i ) + e ( к )

А ^{( к )} =

д ( к - гi )

q ^{( к - (} iz ^- n q )

1 < а < nq nn +1 < 1 < nn + n qq

д ( к ) = -l 1 д ( к - 1) - ... - t _q д ( к - n _q ) + a 1 q ( к - 1) + ... + a i q ( к - n i ) + e ( к )

where the coefficient decision is proposed by (19)-(21).

д ( к ) = - ^ ( к ). / + e ( к )

X = Ир..   qq   ^£ 1—  £ ]                             (12)

. G = [ ^- 5 ( ^{к -} 1)...   ^- 5 ^{( к -} nw )   q ^{( к -} 1)...   q ( ^{к -} n, )]

( nn + rr )!

( rr !)( nn !)

^д ( ^{к )} = L X q ^Ф q ( ^к )

q = 1

Regarding (10)-(12), linear modeling of the robot manipulator is defined by

д ( к ) = [ Ф 1 , Ф 2 ,..., Ф q ] x [ q 1 , q ₂,..., q q ]        (20)

d ( k ) = Ф x q = Э x n

д ( к ) = О [ 5 ( к - 1), д ( к - 2),..., д ( к - n w ) , q ( к - 1), q ( к - 2),..., q ( к - n i )]

9 = Ф„

( nn + rr )!

( rr !)( nn !)

- L h=1

(Ф - 9.) ₉

98„.S„9  ’

Q * = argmin^{ fu ( Q , q )}

1k fu (Q, q) = - L (5(к) - ст(к) x)2 k0

This method is accurate for system estimation, but it has some issues concerning accurate system estimation and robustness. Based on Fig. 1, to evaluate the ARX estimation method, a Laguerre extended ARX technique is recommended. The ARX-Laguerre technique has improved the robustness and precision of the system estimation. To modify the performance of the ARX system estimator, a nonlinear mathematical based system estimator (ARX-Laguerre technique) is used as follows:

d m ( к ) = £ ¹ K ,a ( £ (^^^^ ) n *5 ( к ))

0        j = 1 Z - ^Z a Z - S a

N e - '         ”            ²

G n , q ( к ) + L K n , в ( L ^- Z l ₍1_ £ ^) ⁿ *       (15)

0        j=1 Z ze Z bp q (к)У®п , i(к)

д ( к ) = d m ( к )[ д ( к - 1), д ( к - 2),..., д ( к - n q ) , q ( к - 1), q ( к - 2),..., q ( к- n , )]

n =

(5, 9)

99 , 9)

Regarding Fig. 1, to modify the performance of the ARX-Laguerre technique, the fuzzy logic technique is recommended in this research. Based on the bound of the uncertainties, the primary objective is to present a systematic fuzzy algorithm to model the multi-input-multi-output (MIMO) systems in the presence of unknown parameters. Based on the fuzzy algorithm, this technique consists of the following parts: fuzzification, an IF-THEN rule, a reasoning mechanism, and defuzzification. The primary challenge of system modeling based on the fuzzy algorithm is improving the performance of the knowledge base and inference part. The fuzzy IF-THEN rule is defined as the following equation:

Rule (N): If Г _m is H mm and e _m is H mm then a m is f ^m    (22)

The fuzzy sets, H mm ,H mm , and f^m , can be defined by the following types of the membership function:

^ H , f ^{( m} ) = ^ m . ^ H , f         ⁽²³⁾

The membership function is defined by two inputs (error and change of error) and an output (fuzzy function). To improve the ARX-Laguerre performance, five linguistic variables for inputs are defined. The fuzzy rule table is shown in Table 1.

Table 1. Fuzzy rule base for the fuzzy ARX-Laguerre technique

	NB	NS	z	PS	PB
NB	PB	PB	PB	PS	z
NS	PB	PB	PS	z	NS
Z	PB	PS	z	NS	NB
PS	PS	z	NS	NB	NB
PB	z	NS	NB	NB	NB

Based on (22) and (23), the direct fuzzy reasoning (DFR) defuzzification scenario is defined as

Z ^{n .} H H , f •( ^e m ^{) M h} , f ^{( r} m )

" m ^{( Г} m , ^e m ) =     -   / x- /^ x      ⁽²⁴⁾

^Z ^M H , f •( ^e m )"Мн , f ^{( Г} m )

P = max Mf (" m )           (25)

m

According to this part, the system’s estimation output based on the fuzzy ARX-Laguerre technique is more accurate and robust than the ARX-Laguerre and pure ARX techniques. The fuzzy ARX-Laguerre lookup table is illustrated in Table 2.

Table 2. Lookup table for the fuzzy ARX-Laguerre technique

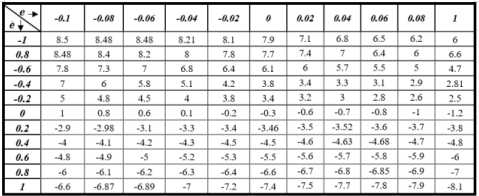
After designing the proposed fuzzy ARX-Laguerre method for system estimation, based on Fig. 1, the adaptive technique is designed based on the following steps. The adaptive system modeling has four main steps: (a) learning the definition, (b) tuning the learning, (c) decreasing the number of rule-bases, and (c) system modeling. The learning part is defined as d (x) = ^al в (x) = O' P( x)

a1 = (a1,a 2,...,am)T(26)

в ( x ) = ( P ¹( x ), P ²( x ),•••, P m ( x )) T

6 ( x ) =

( ^ a l П exP ^{( - (} x ^{a   У в ) 2 )}

L x a _

(SFn

L              xa_

L (a | xa) = aT P( x)(28)

The minimum error is defined to tune the learning techniques as follows:

X = argmin[sup L(a | x) - "(x) ](29)

To obtain the best modeling estimation, the minimum error goes toward zero. The number of rule-bases is one of the main factors in designing the fuzzy algorithm and an online tuner. To reduce the fuzzy rule base and increase the fuzzy performance, we divided the fuzzy system’s modeling into the three sub-fuzzy systems as follows:

^d i⁽ q , q ) = ^a i ^{1 T e (} q , q )

^a\ = ^{( a} L ^a 2 ,..., ^a m ) T

5 2⁽ q , q ) = ^a 2 ^{T e (} q , q )

af = (a2,a22,...,am)T d3(q,q) = a3T e(q,q)

a / = ( a 3 , a 3 ,..., a m ) ^T

After defining the three steps of the learning techniques, the learning part based on the new definition is defined as follows:

a\ =-ex( q, q )• Sap( q, q)(33)

a2 =-d2( q, q). SaP( q, q)(34)

al =-дз( q, q). SaP( q, q)(35)

In the last step, the system is modelled (estimated) by the following equation:

d( q,q,q) = af P( q, q) + a2T P( q, q) + a3T P( q, q)

To minimize the performance index, we defined it as follows:

Z П ( - (

e =

*

^ У в - У в X2

*

У р

N

A block diagram of adaptive fuzzy ARX-Laguerre system estimation is illustrated in Fig. 3. After designing an adaptive fuzzy ARX-Laguerre system estimation, analysis of the system convergences is the next step. Based on (37), to improve the speed of convergence, the system’s error has been rewritten as

(α)2 ϑrr,∂ e =rr ×100%(38)

( ∂,∂

Therefore, we have

( nn + rr )!

( rr !)( nn !)

1-∑  {e}≤α(39)

q = 1

improves the system’s estimation performance in the adaptive fuzzy ARX-Laguerre system estimation technique.

• V.    Results and Discussion

To validate the proposed method, linear system estimation, nonlinear mathematical system estimation, and the proposed method (adaptive fuzzy nonlinear system estimation) are compared. Figure 4 illustrates the estimation performance of the robot manipulator based on the linear (ARX) technique.

Manipulator

^^к-^^к-^^дк-^у а^к-^^к-^-^к-ц)-^

*- 6(,q,q,q')=aYPkq.q'l+afpt.q.q')*^

Fig.3. Block diagram of the adaptive fuzzy ARX-Laguerre system estimation technique

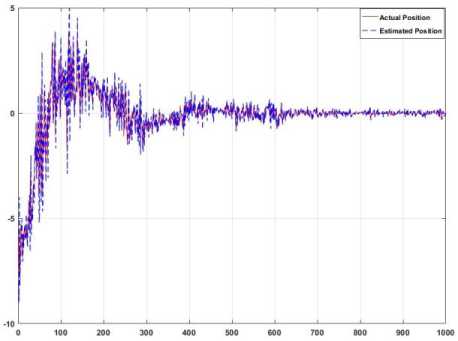
Fig.4. Linear system estimation for the robot manipulator

( n ′ n ′+ r ′ r ′ )!

( r ′ r ′ !)( n ′ n ′ !)

∂n(κ)=  ∑  ∂ Φ (κ)→ h′h′=1

( n ′ n ′+ r ′ r ′ )!

( r ′ r ′ !)( n ′ n ′ !)

∂ _n ( κ ) = ∑ ϑψ4 ( κ ) h ′ h ′= 1

The rate of error for linear system estimation is illustrated in Fig. 5. Based on the figure, the linear estimation technique can estimate with approximately 75% accuracy. The transfer function of linear estimation for the robot manipulator is

S ⁴ + 2 S ³ - 3 S ² - 6 S + 8

S ⁴ + 6 S ³ + 4 S ² - 3 S + 9

( n ′ n ′+ r ′ r ′ )!

( r ′ r ′ !)( n ′ n ′ !)

∂q=Φq-  ∑ q=rr+1

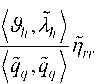
Based on (42), the system’s estimation accuracy is (41) approximately 75%, but this system is modeled to the fifth order. Decreasing the system’s order causes a decrease in convergence speed.

Based on (41), the speed of the convergence is improved compared with other methods. Table 3 illustrates the lookup table performance in the adaptive fuzzy ARX-Laguerre technique for system estimation.

Table 3. Lookup table for the adaptive fuzzy ARX-Laguerre technique

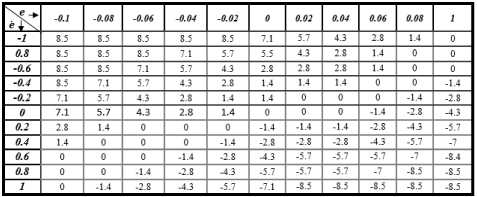
Based on Tables 2 and 3, the adaptive algorithm

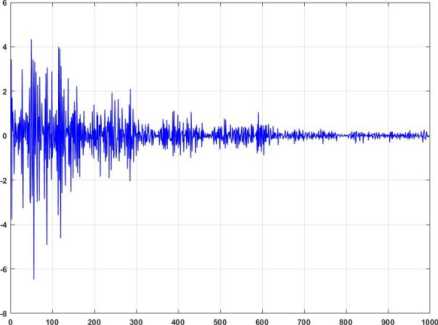
Fig.5. Estimation error (accuracy) for the robot manipulator based on the linear estimation technique

To increase the accuracy and reduce the system’s estimation order, nonlinear mathematical system estimation is presented. Figure 6 demonstrates the estimation accuracy for the robot manipulator based on the nonlinear mathematical based (ARX-Laguerre) method.

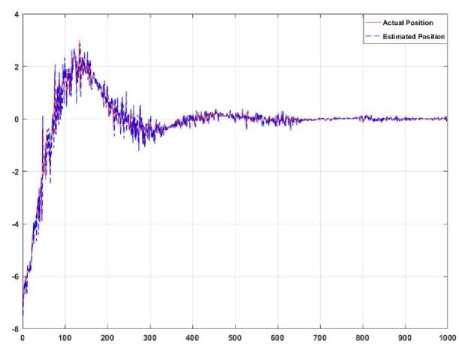
Fig.6. Mathematical nonlinear system estimation for the robot manipulator method estimation and accuracy of the system’s estimation.

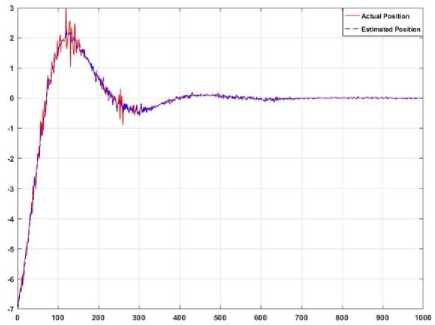
Fig.8. Proposed fuzzy system estimation for the robot manipulator

Based on Fig. 8, the system’s estimation order based on the adaptive fuzzy logic modeling decreases to the second order, and the accuracy also increases to approximately 92%. The transfer function for adaptive fuzzy estimation is calculated as follows

Based on Fig. 6, the transfer function for the ARX-Laguerre robot manipulator system estimation is

12 S ² + 7 S + 2

S ² + 4 S + 19

_н_ 5 S ³ + 2 S ² + 7 S + 12

S3 + 5 S2 + 2 S + 8

The rate of accuracy for this method is approximately 82%. According to (43), the system’s order reduces, which caused an increase in the convergence speed compared with linear system estimation. Figure 7 shows the error of the signal estimated based on the mathematical nonlinear system estimation technique.

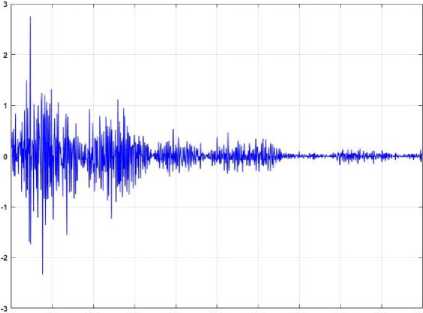
0        100      200      300      400      500      600 TOO 800      900      1000

Fig.7. Estimation error (accuracy) for the robot manipulator based on the mathematical nonlinear technique

Based on Fig. 7, the estimation accuracy compared to linear system estimation (see Fig. 5) is increased; however, the system’s order is decreased. Therefore, the accuracy performance is increased, the system’s order is decreased, and the convergence speed is also increased. Figures 8 and 9 illustrate the power of the proposed

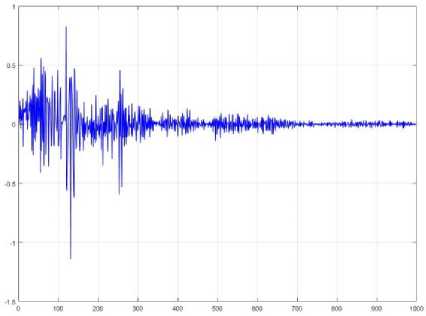
Fig.9. Estimation error (accuracy) for the robot manipulator based on the proposed fuzzy technique

• VI.    Conclusion

Mathematical models are significantly important in the analysis and design of the controller and observer for nonlinear systems (e.g., robot manipulators), but it is impossible to accurately model the physical system by mathematical system estimation. To address this challenge, high speed convergence adaptive fuzzy ARX-Laguerre modeling was presented in this paper. According to the results, the proposed method increased the accuracy from 75% in the linear (ARX) technique to 92%. The proposed method reduced the system’s order for estimation from the fifth order in the linear technique to the second order. Based on the order and accuracy, the convergence speed was sharply increased compared to the linear system modeling. Furthermore, this technique provides a reliable model for the system’s control/observer, system’s analysis, and fault diagnosis of the robot manipulator.

Acknowledgment