Adaptive Observers for Linear Time-Varying Dynamic Objects with Uncertainty Estimation
Автор: Nikolay Karabutov
Журнал: International Journal of Intelligent Systems and Applications(IJISA) @ijisa
Статья в выпуске: 6 vol.9, 2017 года.
Бесплатный доступ
The method for construction adaptive observ-ers (AO) time-varying linear dynamic objects at non-fulfillment of condition excitation constancy (EC) is pro-posed. Synthesis of the adaptive observer is given as the solution of two tasks. The solution first a problem is a choice of the constant matrix decreasing the effect of EC condition. Procedures for obtaining of this matrix are proposed. The matrix specifies restrictions for a vector of parameters AO. The solution of the second problem gives a method of design adaptive multiplicative algorithms in the presence of the obtained restrictions. Procedures for an estimation uncertainty in an object are proposed. They are based on obtaining of static models giving the forecast change of uncertainty. Optimum estimations of the uncertainty are obtained which minimize an error between outputs of the object and AO. An exponential dissipativity of adaptive system is proved. The results of the modeling confirming the effectiveness of designed methods and procedures are presented.
Adaptive observer, identification, uncer-tainty, time-varying system, exponential dissipativity, Lyapunov vector function
Короткий адрес: https://sciup.org/15010935
IDR: 15010935
Текст научной статьи Adaptive Observers for Linear Time-Varying Dynamic Objects with Uncertainty Estimation
Published Online June 2017 in MECS DOI: 10.5815/ijisa.2017.06.01
Construction of adaptive observers (AO) is one of the rapidly developing areas of control theory. The basis of theory AO for the linear class of dynamic systems has been obtained an the end of past century [1-6]. The class of adaptive systems having a special identification representation in space "input-output" was proposed. Despite this, the research in this area continues. In particular, design methods of AO for time-varying objects are proposed. The majority of the approaches are based on the generalization of the results which are obtained for linear time-invariant dynamic systems.
So, problem of combined identification and control of the discrete dynamic system with time-varying parameters is considered in [7]. It is supposed that parameters are piecewise constant, and the modification time is determined by means of the Markov chain. Convergence of adaptive algorithms is proved. The set of criteria allowing minimizing an error of forecasting an output system is applied to improve an efficiency of control. Such approach complicates identification systems. The problem of adaptive identification time-varying nonlinear plant is considered in [8]. It is supposed that the plant state vector is measured and description of a nonlinear part of the system is known. The unknown vector of system parameters approximates Taylor series. The adaptive algorithm of identification is offered. Lüders-Narendra adaptive observer is applied to stabilization of time-varying nonlinear continuous system in [9]. Boundedness of trajectories in an adaptive system is proved.
Methods of adaptive control dynamic systems with variable parameters are proposed in [10]. It is supposed that parameters have the restricted velocity of the change. Boundedness of trajectories in an adaptive system is proved. This approach improves the quality of transients in an adaptive system. It on nonlinear time-varying systems can be generalized.
A multidimensional linear time-varying dynamical system is considered in [11]. Matrixes of state and control are considered as the known functions of time. It is supposed that the linear part of the system depends on an unknown parameter vector. The adaptive Kalman filter for a state estimation and system parameters is offered.
Considered methods and algorithms do not allow ensuring the unbiasedness of obtained estimations [12, 13]. Explain it to that the law of the change parameters is unknown. Therefore, the majority of approaches on the qua-si-stationary hypothesis are based.
The solution of design problem AO can be based an application: (i) different methods of time-varying parameters approximation [8]; (ii) the compensating control influences [9, 14]. Choice of the reference model for AO in [14] is realized on the basis of the analysis the a priori information. The law of parameters objects change under the uncertainty is usually unknown. Therefore, the object as a system with parametric uncertainty is considered.
Adaptive observer application for the control of stationary uncertain objects is given in [3, 15]. The case when uncertainty is a discrepancy of a model to plant (structural disturbances) is studied. Such disturbances are called non-modeling dynamics. Algorithms which ensure robustness to these disturbances are designed.
So, the problem of time-varying systems identification is topical. The condition of the excitation constancy is the basis of the design effective adaptive systems. This condition often is not fulfilled. Stability AO under these conditions was not studied. The second important problem is the parametric disturbances estimation in a system. As a rule, parametric disturbances suppose the restricted. A posteriori method of the parametric uncertainty estimation was not offered.
We propose the method of design AO for a linear timevarying dynamic object at condition EC non-fulfillment. The problem of synthesis the adaptive observer is divided into two subtasks. The solution of the first problem gives a choice of the constant matrix alleviating condition EC. This matrix superimposes restrictions on the parameters vector AO. The method of the matrix construction is proposed. The set (vector) of multiplicative adjusted parameters (MAP) is introduced at the second stage of the problem solution. The method of the dimension choice MAP is proposed. Adaptive identification is reduced to the design problem of algorithms under restriction. The method ф -algorithms [15, 16] is applied to its solution. Next, the problem of uncertainty estimation in the object is considered. Two approaches are offered to the solution of this problem. The first approach allows obtaining static model on the basis which the uncertainty estimation is determined. The adjusted parameter is introduced for raise of an exactitude of the estimation. It allows minimizing a total the prediction error. The second approach is based on the construction of a static model depending on current values of parameters AO. We introduce the adjusted parameter. It raises the exactitude of the uncertainty estimation. Boundedness and exponential dissipativity of trajectories of the adaptive system are proved. Computer modeling AO is fulfilled.
The work has the following structure. Section 2 contains the problem statement. The equation AO is obtained in section 3. The control compensating uncertainty is introduced. Main assumptions concerning properties of the system are considered. Parametrization of the control for increase of identification accuracy is performed. The parametric variable allowing adapting control to the existing uncertainty is introduced. The design of adaptive algorithms at non-performance of excitation constancy condition is proposed in section 4. Multiplicative parameters are introduced for fulfillment EC in a special parametrical space. ф -algorithms of the parametrical variable tuning are designed. Variants of the accounting of a posteriori information on the system are c o nsidered. Section 5 gives the description of a matrix H choice ensuring contraction of parametrical space AO for fulfillment EC. The condition of dom i nation is algorithm basis for the design of the matrix H . The problem of the uncertainty estimation is considered in section 6. The task solution is based on the introduction of a variable estimating uncertainty in the system. The adjusted coefficient ll before this variable raises the estimation accuracy. Properties of the adaptive system are researched in section 7. Boundedness of adaptive system trajectories is proved. Properties of AO with various algorithms for control and adaptation are researched. Obtained results are based on the application of Lyapunov vector functions. The proof of main statements is given in appendices. Results of modeling are presented in section 8. The conclusion contains the short review of obtained results.
-
II. Problem Statement
Consider the object described by the equation
x ( m ) + am(t ) x ( m ) + ...+ ax ( t ) x = b ( t ) r , y = x , (1)
where 0 (t ) = [ a ( t ) a 2 ( t )... am ( t ) b (t ) J T , r e R , y e R are input and output, 0e G6 , Ge c Rm + 1 is restricted and a priori an unknown area.
Components of the vector , ( t ) have the form
, (t) = ^ + A, (t) , i = 1, m +1, where |a, (t)||<, = const > 0, ^ = const.
The laws of change , ( t ) also are unknown.
Assumption 1 . The change velocity A , ( t ) is restricted and unknown.
Assumption 2 . The vector A0 ( t ) = 0 ( t ) -0 ° belongs to set
A0e G , \G^, (2)
where 0 ° = ^ ax ° a ° ... a ° b 0 J .
-
(2) is the condition of uncertainty. The experimental information on an object has the form
Io ={r(t)>y(t) t e J} , where J c R is the specified interval of the time.
The condition EC is not fulfilled for the input r ( t ).
Problem: design for (1) adaptive observer that the condition was satisfied lim y(t)- y(t) < ny,(3)
where y ( t ) is output AO, n - °.
-
III. Equation of Adaptive Observer
Write the equation (1) in the form y = 0TP + f (y, r, A0),(4)
where P e R 2 m is the generalized input representing an output of the auxiliary filter
P1 = [Л + Л] P1 + [iTylTr]T ,(5)
P = [ y PT r PT ] T , P = [ PT PT ] T , P ∈ R 2 m - 2 is the vector of auxiliary signals obtained on the basis of transformation r ( t ) and y ( t ); + is the sign of the direct sum of matrixes; Λ ∈ Rm - 1 is the diagonal matrix with λ < 0 ( i = 1, m - 1 ) ; I ∈ Rm - 1 is unit vector; Θ ∈ R 2 m is a vector corresponding Θ 0 ; f ( y , r , ΔΘ ) ∈ R is a component depending on the parametric disturbance ΔΘ in (1).
Assumption 3. The input r ( t ) does not satisfy a condition of constant excitation.
Assumption 4. f ( y , r , ΔΘ ) <∞ at | r ( t ) | <∞ .
Apply to the object described by the equation (4), adaptive model [17]
y ˆ =- k ( y ˆ - y ) + NTHTP + u , (6)
where H ∈ R 2 m × l is a matrix with constant parameters, N ∈ Rl is a vector of adjusted parameters, u ∈ R is a control, l < 2 m .
Present u ( t )in the form
u(t) =DT(t)P(t) ,(7)
where D ∈ R 2 m is some restricted vector.
Write the vector D as
DT(t) = µ(t)D,(8)
where D ∈ R 2 m , II D ( t ) II ≤ d , d > 0 is some number, µ ( t ) ∈ R is controlled variable.
We suppose that
µ(t)∈Gµ ={µ∈R:I µ(t) I≤1 ∀t≥t0}.(9)
The choice of the vector D ensures fulfillment of the condition (9).
-
IV. Design of Adaptive Algorithms
We propose an approach to the design of the adaptive observer at non-performance EC. The preliminary estimate H of parameter vector the object (4) is obtained. The multiplicative tuned vector N ( t ) at matrix H has introduced that fulfillment of conditions EC and (3) to ensure. Adaptive ϕ -algorithm for vector is obtained. It is based on the accounting of existing restrictions
Go to the design of adaptive algorithms for the vector N(t) and the variable µ(t). Write the equation for an identification error e(t) as e=-ke+NTHTP-ΘTP-f(y,u,ΔΘ)+µz, (10)
where z = DTP .
We see from (10) that the vector HN ( t ) should approximate unknown parameters vector of the object (4). As parametric uncertainty exists, e ( t ) cannot be reduced to zero. Apply control u ( t ) to ensure fulfillment of the condition (3).
Linearize function f ( ⋅ )
f ( y , u , ΔΘ , t ) =ΔΘ T ( t ) P ( t ) , (11)
where ΔΘ ( t ) is some vector.
We assume that on the basis of the made assumptions
| f ( y , u , ΔΘ , t )| ≤ ρ f = const ≥ 0. (12)
Choose dimension l the vector N ( t ) on the basis of frequency properties the input r ( t ) . Designate the approximation error Θ + ΔΘ ( t ) with the vector HN ( t ) as δ N ( t ):
δ ( t ) = HN ( t ) -Θ-ΔΘ ( t ) .
δ ( t ) satisfies (2) and depends on the parametric uncertainty of the object (4). Uncertainty depend from δ ( t ) and satisfies the condition (12). Therefore, the condition is true for Θ ˆ ( t ) = Θ+ ΔΘ ( t )
Θ ˆ( t ) ∈ G k A ⇔ α ˆ θ ≤ Θ ˆ( t ) ≤ α θ .
Then we have
II HN ( t ) II≤ α N , α N <∞ .
We obtain from δ ( t ) inequality
ν=αN -αθ≤ δN(t)≤ αN -αˆθI=ν1.(13)
Then the vector N ( t ) at a corresponding choice of matrix H belongs to set
N∈GN={N∈Rl: ni(t)I ≤1 i=1,l }.(14)
Write (11) as e = -ke+δTP+µz .(15)
Transform the equation (15) to the form e = -ke+σTP-σTP+µz, where aN(t) = HN(t)-0, ^ = A0(t) . Let h^ = ^TP .
Apply the method ф -algorithms [15, 16] to the design of adaptation algorithms. Consider Lyapunov function Ve (t ) = 0.5 e 2( t ) . F- form is true for the derivative X ( t ) = V e ( t )
X = - ke 2 I T N ( N ) Ф N ( e , N , H , F ) + e CT T T F + e ^ z , (16)
Where
Ф N = eF ( I T D (I N ) I ) - 1 ^ N , T N ( N ) = I T D (I N ) I ,
|N | is the absolute value of the vector N ( t ), D (| N |) is diagonal matrix from the vector N , I e Rl is the unit vector.
Obtain from (16) ф -algorithm for adaptation the vector N ( t )
N = - e r p ( N ) H T F , (17)
where Г e Rl x l is a symmetrical positive-definite matrix, P ( N ) is a belonging matrix indicator N e G x .
Various methods of the definition P ( N ) are applicable.
If the indicator P (N)to present in the form f I, N (t) e Gn
P ( N ) = l’ N
[ 0,, N(t) g G„ that multiplicative ф -algorithm for N(t) has the form
^ = I-erHTF, N(t) e Gn , [ 01, N (t) g G n , where It, 0Z unit and zero matrixes l x l.
Matrix H for accuracy raise can be computed on each interval of a quasi-stationary object.
Design the control law for the variable a(t). Let conditions (8), (9) are satisfied. Determine the adjustment law a(t) from the condition min max V (n, SN, t) .(19)
n Sn eN max V(t) on SN (t) is obtained on domain boundary (13), that is at such value SN (t), when ||Sv (t)||=4 • Therefore, transform x(e, A, t) to form
X - -ke2 + Tц (e, A, z) Фa (e, A, z) + |e| ||Sn|| IIPII, where Тд = |e||DTF|, Ф^ = Asgn(e)sgn(DTF).
As a e G^ the adaptive observer is robust to uncertainty h A = F T F , if
||D|| > c(V1),(21)
where c ( v ) > 0 is some number.
Obtain the following tuning ф -algorithms of the variable a ( t ) on the basis (20) and (19):
-
i) static Μ -algorithm
A(t) = -Ys sgn(e(t)) sgn(DTF(t));(22)
-
ii) dynamic Μ -algorithm
A( t) = -Ya, sp(A)sgn (e( t)) sgn (DT F(t));
-
iii) dynamic Μ - algorithm
A(t ) = -Ya P (A) e (t) DTF(t),(24)
where P ( a ) is the belonging indicator a ( t ) e G^ , Y s > 0, Y a > 0, Y a , s > 0.
Other algorithms for a ( t ) can be obtained from the condition x - 0 .
-
V. Choice of Matrix H
Consider the equation (4). Apply the operation of the differentiation to determination y . Designate the obtained variable as yd (t ). Choose time gap Jd c J the change y so that system properties on it were homogeneous. It means that the trajectory y ( t ), and, hence, y ( t ) should not have structural modifications.
Consider on the interval J the equation
Уа = HTF, where H e R2 m, H = HI, I e R2 m.
Apply the least-squares method and obtain the vector H as the problem solution min (y - ya )2 ^ H.
H
Demands to the estimation H .
H1. H ensures the following condition of dominance
У(t) Уа (t) for almost Vt e J c J, where J contains all t, since some t > 4 > t0.
H2. Elements of vector H ensure the performance of the adaptive system.
Condition H2 is very important, as tuning of vector N ( t ) in (6) depends on the elements of the vector H . As l < 2 m we consider only such estimations N ( t ) which ensure minimization of functional
Q ( N ) = ( H ( H ) N ( t ) -0 ) 2 .
Remark 1. The estimation H is obtained from the quasi-stationary condition of change system parameters. This estimation has the approached character, sufficient for implementation of the adaptive system.
Remark 2. If traj e ctories of the adaptive system are not restricted the set H , fulfill one of following operations.
-
1. Obtain the estimation H for t e J^ , where J M # J * .
-
2. Change dimension l of the vector N ( t ). It will lead to the replacement of the vector H by the matrix H .
-
VI. Uncertainty Estimation
Obtaining D in the conditions of uncertainty is the complicated problem. Therefore, apply the following approach. It is based on obtaining of a variable for the estimation h ( t ).
Construct model
У d = H J P (25)
for prediction of the variable y ( t ), and compute values of the error sd (t ) = y ^ ( t ) - yd (t ) . sd ( t ) is the uncertainty estimation in the system.
Remark 3. We have introduced the vector H to distinguish it from the vector H used for the formation of the matrix H in model (6).
Present model (6) and the equation for the identification error (15) in the form
SED : У = - k ( y - y ) + N T H T P + p£^ , e = - ke + r T P + gd , (26)
Me = -Yse^d, where gd = иуу -oTP, lu is the adjusted parameter.
p adjusted level ^ that of disturbance effect to compensate in the adaptive system. Disturbances are a result of the application the model y^ = H T P and the action h д ( t ) .
Remark 4. Demands to the vector H considered in section 5 should be considered, when the variable ^ ( t ) is determined.
Another approach is based on obtaining of the uncertainty estimations on the basis of current adaptation results use. Apply model yd, N = NT HTP, (27)
and determine the error ^ ( t ) = y ^ ^( t ) - yd (t ) . ^ is the current estimation of the uncertainty h ( t ).
Use of the model (27) complicates the adaptation process. But work quality of adaptive system under some conditions improves at the application of the model (27). Here dimension of the vector N ( t ) has the significant effect. Therefore, the compromise necessary to observe between dimension of the vector N ( t ) and properties I .
Write the model (6) and the equation for identification error (15) for the case (27) as
SEN : y = - k ( y - y ) + N T H T P + p^ , e = - ke + ^NP + g N , (28)
Pn = -7Ne£N, where gN = pNeN - a^P, p is the tuned parameter.
-
VII. Properties of Adaptive Systems
Consider properties of the adaptive system ASss which is described by equations (7), (8), (15), (17), (22). Boundedness of trajectories follows from the following assertion.
Theorem 1. Let conditions are satisfied: 1) function Ve (t) = 0,5e2 (t) is positive definite and satisfies the condition inf V (e, t) ^ ^ ; 2) assumptions 1, 2 for the ob-| e| ^да ject (1) are fulfilled; 3) the parameter N(t), p(t) of the model (6) belong to restricted areas G , G . Then all trajectories of system ASss are restricted and fair estimations
t
J ( 2Ve ( r ) - Y s ^ 4 2 V e ( r ) ) d r < V ( t о ) - V ( t ), t 0
V e ( t ) < I ^ P maxl I 5 " ( t )ll + Y s U z I , (29)
t where д = min |^TP|, uP = max||P(t)||2, и = max|z(t)|,
-
V ( t ) = V e ( t ) + ∫ δ N T ( τ ) Γ- 1 Ψ N ( N ) δ N ( τ ) d τ . (30)
t 0
The proof of theorem 1 is given in Appendix A.
The theorem 1 shows that all trajectories of the adaptive system ASss are restricted. Limiting properties ASss -systems depend on the work of the adaptive algorithm (17) and the control law (22) variable µ ( t ). Μ -algorithm ensures fulfillment of the condition (3). The decrease of the error e ( t ) depends on the choice of the parameter γ Μ -algorithm.
Consider ASds -system described by equations (7), (8), (15), (17) and (23).
Theorem 2. Let conditions of the theorem 1 are satisfied. Then all trajectories of the system ASds are restricted and fair estimations (29) with γ 2 = 1 , and
t
∫ 2 V e ( τ ) d τ ≤ V ( t 0 ) - V ( t ). t 0
So, Μ , Μ -algorithms ensure fulfillment of the target condition (3). Specific properties of algorithms do not allow improving the quality of the adaptive system work.
The proof of theorem 2 is given in Appendix B.
Consider ASd -system described by the equations (7), (8), (15), (17) and (24).
Theorem 3. Let conditions of the theorem 1 are satisfied. Then all trajectories of the system ASd are restricted and fair the estimation
Ve ( t ) ≤ υ P 2 max δ N ( t )II2.
The proof of theorem 3 is given in Appendix C.
We see that the condition (3) with π = 0 in ASd -y Nµ system can satisfy. It is possible if the vector HP(t) is constantly excited.
Consider properties of the algorithm (18). The equation for an error writes in the form e = -ke+σTP-σTP+µz, (31)
where
σ N ( t ) = H ( N ( t ) - N Θ ) = H Δ N ( t ), Θ= HN , σ = ΔΘ ( t ).
Definition 1 [18]. The non-positive quadratic form
W ( Y , X ) has M -property or W ( Y , X ) ∈ M , if it is representable as
W(Y,X)=-cyIIY II2 +cxyWxy(Y,X), for any Y∈ Rm , X∈ Rn in limited area
Ω ={Y∈Rm,X ∈RnIIIY II2+ X 2≤α, α≥0}, where IIY II is Euclidean norm of a vector Y , c > 0 , c ≥ 0 , W (Y,X) is some function.
Definition 2 [18]. The non-positive quadratic form
W ( Y , X ) has M + -property or W ( Y , X ) ∈ M + , if it is representable as
W(Y,X)=-cyY2+cxX 2, for any Y∈ Rm , X∈ Rn in the restricted area Ω , where cx ≥ 0.
M + -property is an indication of a constructive completeness of the quadratic form W ( Y , X ) . It allows reducing the analysis of properties W ( Y , X ) to an estimation of characteristics corresponding M -matrix [19].
Definition 3. The vector P ( t ) = HT P ( t ) , P ∈ Rl is constantly excited with level α or has property PE , if
PEα: PH(t)PHT(t)≥αIl for some α > 0 and ∀t≥t on some interval T > 0 .
The system (1) is stable, and the input r ( t ) is restricted. Therefore, property PE for the matrix B ( t ) = P ( t ) PT ( t ) present as
α I ≤ B ( t ) ≤ α I ∀ t ≥ t , (32)
where α > 0 is some number.
Consider Lyapunov function
V N ( t ) = 0.5 Δ T N ( t ) Γ- 1 Ψ N ( N ) Δ N ( t ).
Let the estimation for V ( t ) is right
0.5 λ l - 1( Γ ) Δ N ( t )2 ≤ V N ( t ) ≤ 0.5 λ 1 - 1( Γ ) Δ N ( t )2, (33)
where λ ( Γ ), λ ( Γ ) are the minimum and maximum eigenvalues of the matrix Γ , Γ = Γ T > 0 .
Lemma 1. Function V ( t ) has M + -property, if
■ Зс^Г) 4
У N — N N + е , where 3 > 0 is some number.
The proof of lemma 1 is given in Appendix D.
Ensure the condition Ve g M + .
Lemma 2. Function Ve ( t ) has M + -property, if
V e — " kV e + 2 “^ ' ( Г ) V N + 1 ( U P max |КГ + U z ) , (34)
where || ^ || is the Euclidean norm of the vector aN .
The proof of lemma 2 is given in Appendix E.
Remark 5. M + -property functions Ve and VN are conditions of the exponential dissipativity [20] the adaptive system. Passivity conditions of the adaptive system follow from these properties.
Show the exponential dissipativity of the adaptive system (18), (31). Apply the method of Lyapunov vector functions.
Let such functions sp (t ) > 0 exist that
-
V ( t > t 0 ) & ( V ( t 0 ) — S p ( 1 0 ) ) , p = e, N . (35)
Then we will reduce the analysis of properties the adaptive system to research of the following system of inequalities
V n 4 3 а3Х ( Г )
— 3--
L 3 4
Stability conditions of the matrix A have the form [19]
—m1( AV ) > 0, m2( AV ) > 0, where m, m are diagonal minors of the matrix A . These conditions have the form k > 0,
k> 4 I2aX ( Г )
3 ^aX ( Г )
So, following statement is true.
Theorem 4. Let conditions are satisfied: 1) Lyapunov functions
V n ( t ) = 0.5 Д N ( t ) Г " ’ V N ( N ) Д n ( t ) V e ( t ) = 0.5 e 2( t )
have infinitely big limit at |e(t)| ^ да, IIдn (t)|| ^да;2) the vector P(t) is piecewise continuous restricted and Ph(t) g PE„ ; 3) equality eДNPn = 3(ДN^nДN + e2) with 0 < 3 fair in area Ov (O); 4) V g M+, V, g M+; 5) the estimation (33) is fair for the function V(t); 6) the upper solution for Lyapunov vector function V(t) = [V(t) VN(t)] T satisfies the equation (37); 7) uncertainty aK (t) in (31) is restricted: ||^ (t)|| < ид Vt > t0, where ид > 0 is some number. Then the system (18), (31) is exponentially-dissipative and estimations are fair да
V(t) — eA(•"•0)S(10) + JeAV(t—T)Fv(t)dr , t0
( u p max|| ст д ( t )||2 + и
V ( t ) — ’ ( U p max I Ь д ( t )l|2 + U z ) Z ’ ( t ) I • ^” ,
Obtain for (36) the vector system of comparisons
t where S1 (t) is the first column of the matrix J eAV (t—r) dr, t0
S = AKS + F V , (37)
if
where A g R 2 x 2 is M -matrix of the form
4 2 OZ , ( Г ) >0
3\] aX ( Г ) .
AV
2 a X ( Г )
k
4 3 а3Х ( Г )
— 3--
L 3 4
sN
— U p max kPt
II ^ д ( t )||2 + U )
The theorem 4 shows that the algorithm (18) is identifying if the vector P ( t ) satisfies the condition (32). Dissipative properties of the system depend on an applied control algorithm of the variable д ( t ). The control algorithm properties of the variable ^ ( t ) are considered above.
Consider the properties of the adaptive system with the estimation of uncertainty h ( t ). Designate system SED
and (18) as ASEDNp . Boundedness of the variable ^ ( t ) follows from the method of its obtaining.
Theorem 5. Let conditions 1), 2) theorem 1 are satisfied. Then all trajectories AS - system is restricted and the estimation fair
V e (t ) < 71 2 ( « max I |A N ( t )||2 + max h A ( t ) ) . (38)
The proof of theorem 5 is given in Appendix F.
Consider ASEN -system SEN and (18). Let such number Mn exists that h ( t ) = Mn£n (t ) . Designate ^M n = M n - M *, n .
Theorem 6. Let conditions 1), 2) theorem 1 are satisfied and: (i) dN < г^ < dN , where dN > 0, dN > 0 are some numbers; (ii) positive definite function
V (t) = 0.5/^1 (5mn(t))2 satisfies the condition inf V (e, t) ^^ . Then all trajectories of the system II X ||^<ю
ASEN are restricted with the estimation n M n
t
V ( t ) < V ( 1 0 ) - 2 к J Ve ( t ) d T , t 0
Where
V ( t ) = Ve ( t ) + V m n ( t ) + V ( t ) =
0.5 e 2( t ) + 0.5 Y N ( SM n ( t ) ) 2 + 0.5 ^ 2 ( t )l' V . ( t ).
Let further conditions are satisfied: (iii) M+ - properties for V , V have the form k 2dN
k
U —- ^ N ^ N
A M n
V M N j
a maxiA n Ii2
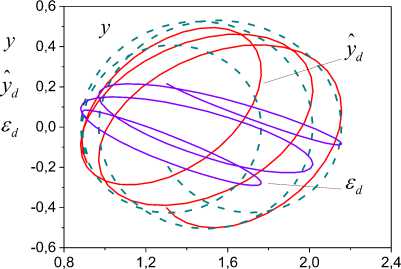
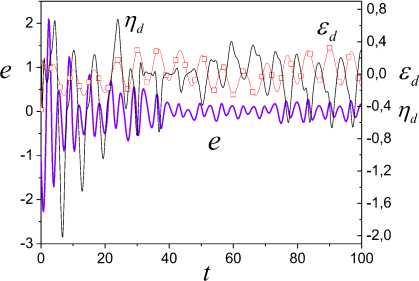
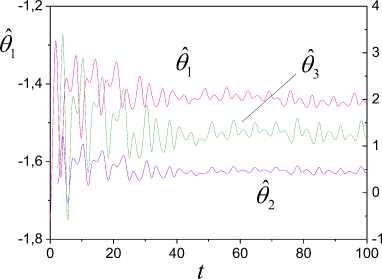
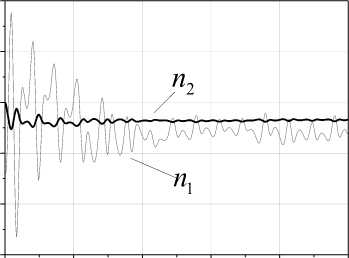
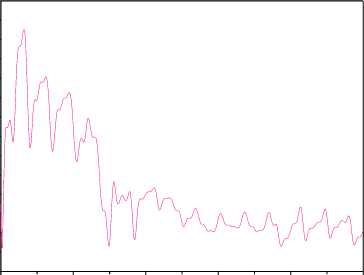
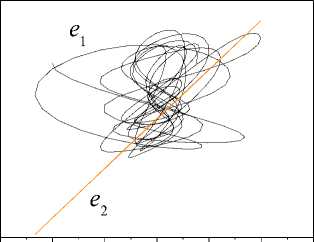
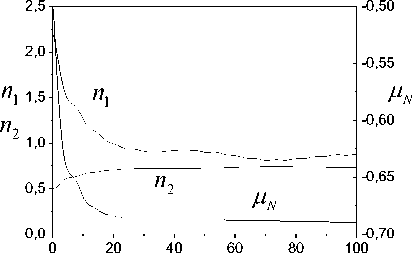
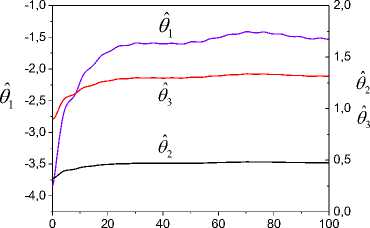
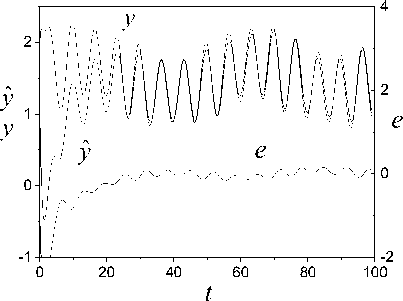
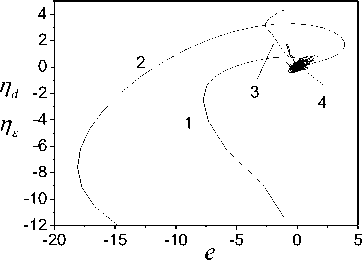
(iv) such functions sp (t) > 0 exist that vp(t) (v) the upper solution of the system (39) satisfies to the vector system of comparison Se,Mn (t) = AMNSe,Mn (t) + FMn , Where Se, Mn =[ sesMN jT ; (vi) uncertainty h (t) = o^ (t)P(t) in (31) is restricted. Then ASEN -system is exponentially-dissipative and estimations are fair t V(t) < eAMN (t-t0)Se,m (10) + J eA™(t-T)Fmn(t) dT , t0 V (t) < a max I iAn 112 ei, m (t) । t ^", If 228 к > 0 , k dNYN > g dN , t where S1 (t) is the first column of the matrix J eAV(t-T) dT . t0 The proof of theorem 6 is given in Appendix H. Theorem 6 shows that properties the ASEN -system depend on the quality of work the adaptive algorithm (18). Therefore, the maximum dimension chooses N(t) for the decrease of the misalignment A^ (t) . Explain it to that quality of the tuning N(t) influences on the magnitude of the error e(t) and г . Consider object (1) second order with parameters av (t) = -2 + 0.3sin(0.04^t) , b = 1.5 a2 (t) = -3 + 0.5 sin(0.09^t) ., r(t) = 2 + sin(0.3^t) . The equation (1) was integrated with the step 0.2s. x(0) = 2, x(0) = 1. The informational set Io is obtained for the object (1). Parameter of the auxiliary filter (5) Л = -1.5, P (0) = 0, Pr (0) = 0. к = 1. Consider SED -system. Apply the following approach to the definition of the variable г. Fulfill segmentation of values the variable y(t) on set J on the basis of observance of a condition structural homogeneity of modification y(t). Apply the method described in section 5, and find the vector Hd on each subinterval J c J . Choose the value H ensuring the maximum of determination coefficient for model ;yd = HTTP. We will obtain the vector Hd =[0.28; - 1.19;0.59]T on the interval [39.2; 79.2] s. Fulfill the prediction of change y(t) by means of the model ya = HTTP and determine ^. Next, use the obtained variable ^ for implementation SED -system. Show change ed in Fig. 1. Fig.3. Change error e , ^ and the uncertainty estimation n . y Fig.1. Uncertainty estimation in object (1) on the basis of application SED -system. Determine the matrix H for implementation SED -systems. Apply the approach described in section 5. The vector H = [-1.75;0.65;1.8]T in (6) is obtained on the time gap [12.2; 19.2]s. The matrix H is obtained on the basis H Changes of the error e(t), ^ , and the calculated current value n = ^A uncertainty are shown in the Fig. 3. Show in the Fig. 4 change of parameters 6 (t) 62 (t) 63 (t) J = HN(t). Tuning of the variable ^ in system (26) is presented in Fig. 5. Parameters of object (1) after reduction of its equation to the form (4) varied in ranges: 6 (t) = [-1.95;-1.25], 6 (t) = [0.4;0.95], 6 = 1.5. -1.75 0.65 1.8 The vector N(t) e R2 is tuned by means of algorithm (18). Matrix Г in (18) has the form Г = diag (0.005; 0.05). Factor yg in (26) ye = 5 . Results of work SED -system are shown in Fig. 2-6. The Fig. 2 represents the process of tuning of the vector N(t). ^ Fig.4. Parameter estimations of the object (4), obtained by means of system (26). 2,0 n1 1,5 n2 1,0 0,5 0,0 -0,5 0 20 40 60 80 100 t Fig.2. Tuning of the vector N(t) by means of the algorithm (18). 4 vs -2 -4 0 20 40 60 80 100 t Fig.5. Change of the parameter ^ the system (26). The analysis of obtained results confirms workability the adaptive SED -systems. Explain such change: (i) application of a static model (SM) for uncertainty identification; (ii) obtaining of parameters SM on the given time gap. This note is true for change of elements of the vector N(t). Work of the adaptive observer is stabilized at the increase of parameters tuning time. We give the comparison of results work SED -system with one and two adjusted parameters (Fig. 6). Designate relative values of errors SED -systems with N∈Rand N∈R2 as e(t) and e(t). Except the initial stage of tuning of the vector N(t) the model (26). The Fig. 6 shows of the framework change described by the function f (e ) : e (t) → e (t) . S shows the comparative position e(t) and e(t), starting t ≥ 19.2 s. We see that an accuracy of the adaptive system with N∈R is lower, than with N∈R2 . The framework S is more informative than change e on t the plane (t, e) . We have made this conclusion on the basis of the theorem 6 for the ASEN -system. It is also true and for ASED - NµN Nµε system. 0,6 0,4 e1 0,2 e20,0 -0,2 -0,4 -0,6 -0,75 -0,50 -0,25 0,00 0,25 0,50 0,75 e2 Fig.6. Comparison of the work quality of the system (26) with one and two adjusted parameters Consider the work of ASEN -system. The matrix NµN H has the form (40), N(t)∈R2 . Matrix Γ in (18): γ=diag(0.004;0.0007) . The factor γN SEN -system is 0.0006. Show results of the work ASED -system in NµN Fig. 7 - 10. The Fig. 7 represents tuning of the vector N(t) the system (28). Compare these results with the parameters tuning of the system (26). We see that adaptation process in the ASEN -system has monotonic character. Explain this the adequate estimation of the uncertainty h(t). Present in the Fig. 8 identification results of the object (4), obtained by means of the system (28). The Fig. 9 contains results of the work ASED -system. We see NµN that the adaptive system is exponentially-dissipative. t Fig.7. Tuning of model parameters, the system (28). t Fig.8. Estimations of parameters the object (4) obtained by means of the system (28). Fig.9. Estimation of adequacy work system (28) Fig.10. Identification results of the uncertainty by means of systems (26), (28) Loop estimation work results of the uncertainty object at different parameters of systems (26), (28) are presented in the Fig. 10. The designations applied in Fig. 10: 1 is systems (26) with N(t) g R and the static law n = 0.9^ of the estimation h^ (t); 2 is systems (28) with N(t) g R2 and the static law n = ^ ; 3 is systems (28) with N(t) g R2 and the algorithm A = -yNesN ; 4 is systems (26) with N(t) g R and the algorithm A = -y£ eed . Results are presented in the form of the frameworks described by functions f : e(t) ^ n (t) , i = d, N . The analysis of the Fig. 10 shows that best performances have the adaptive SEN -system. Remaining variants of the considered systems have the large time tuning and a low accuracy of the uncertainty estimation. The method of construction adaptive observers for time-varying linear dynamic objects is proposed at nonfulfillment of the condition excitation constancy. The problem of synthesis AO is divided into two subtasks. The first problem proposes the procedure to the choice of the constant matrix, allowing decreasing effect the excitation constancy condition. This matrix superimposes restrictions on parameters AO. The solution of the second task gives to the choice of adaptive algorithms on the basis of the obtained matrix. We introduce the set of multiplicative adaptive parameters, allowing identification problem under restrictions to solve. Adaptive algorithms of multiplicative identification are designed. Two methods of an estimation uncertainty are proposed for improvement performance of the adaptive observer. The first method is based on a design of a static model for the uncertainty estimation. We introduce the parameter improving the accuracy of the uncertainty estimation. The second method gives the uncertainty estimation on the basis of parameter current values the adaptive observer. The exponential dissipativity of the adaptive observer is proved. We present the results of the modeling confirming effectiveness of designed methods and procedures. Appendix A. Proof of Theorem 1 Consider Lyapunov function V(t) (30). The choice of the second component in the right part (30) is substantiated in [15]. Find the derivative V(t) on motions ASss -system. Obtain after simple transformations for V(t) the inequality V <-2Ve - ys^V, (A.1) where q = minpJTP . Apply the condition 1) of theorem 1. Then we obtain from (A.1), what V(t) < 0 and the system ASsn is stable. Integrate (A.1) on the time and obtain t V(to) -J(2V(t) + yq42 V(t) )dT > V(t). t0 As V (e,^, a) satisfies the condition 1) theorem 1 then all trajectories of the system ASss belong the area Gt ={(e, N, a) : V(t) < V (t0)} . Then we have the estimation for ASss -system t J(2Ve(t) + rq42Ve(t))dT< V(to) -V(t). t0 Obtain the inequality (29). Consider V(t) Ve =-ke2 +eSNP-Ys |e||H< (A.2) Use the inequality [21] - az1 + bz< —az— + —, a > 0, b > 0, z > 0 22a and transform (A.2) to the form Ve <-k!e ’ + Tk(l^'|И + Y.lz )2. Present (A.3) after simple transformations as Ve<-kVe +11 UP max k V t (A.4) where op = max|p(t)||2, uz = max|z(t)|. From (A.4) we obtain the estimation (29) for V(t). Appendix B. Proof of Theorem 2 Consider Lyapunov function t V(t) = Ve(t) + J^T (t)Г 'TN (N)3N(t)dT t0 . t +J ^vT^rtsT a (Ц)Ц(т ) dT t0 Transform V(t) on motions of the system ASds to the form V<-2Ve . (B.1) V satisfies to the condition 1) theorem 1. Obtain from (B.1) the inequality V(t) < 0 . ASds -system is stable. Integrate (B.1) ∫t2Ve(τ)dτ≤V(t0)-V(t) . (B.2) t0 Obtain from (B.2) the boundedness of trajectories ASNdsµ -system. The estimation for V has the form Ve≤-k2e2+21k(δNIlliPII +IzI)2. Obtain from (A.2) the estimation (29) with γ2= 1 . Consider Lyapunov function Veµ(t)=Ve(t)+γd-1∫tµ(τ)Ψµ(µ)µ(τ)dτ=Ve(t)+Vµ(t). t0 Present V as eµ Ve+Vµ=-ke2+eδNTP≤-ke2+υP max δN(t)II2. Then Ve(t)≤υP2 max δN(t) 2-∫Vµ(τ)dτ. t0 Let Ψ(µ) =1 . Then have Vµ(τ)dτ= 1(µ2(t)-µ2(t0))>0 . t0 2γd So Ve(t)≤υP2 max δN(t) 2. Consider V(t) VN(t)=-eΔTNPH . (D.1) To ensure property V(t)∈M apply the approach [15, 18]. Let for (∀t ≥ t*> t )&(∀(e,Δ )) ∈O (O)) the condition is satisfied O ={0, 0m}⊂R×Rm×J0,∞, where O = {0, 0l} ⊂ R×Rl×J is the equilibrium position of the system, Oν (O) is some neighborhood of the point O , 0l∈ Rl is the zero vector, t∈ [0, ∞] = J, ϑ> 0 is some number. Transform (D.1) to the form [15] VN(t)=-ϑ(ΔTNBHΔN +e2) . Next use (32) and the approach described in [18]. Let Ψ (N)=P(N)=I . Then obtain VN ≤-3aϑΔTNΔN + . 2ϑe2≤-3αϑλ1(Γ)V +4ϑV⇔V∈M+ 3 4 N3eδ Apply (31) and present V as V ≤ -ke2+ IeI δNTPH +σΔTP+µz I . (E.1) We obtain from (E.1) V∈M . Ensure the condition V∈M+. Apply the proof of the theorem 1 and obtain Ve ≤-ke2+ 1(ΔTNPH +σΔTP+µz)2≤ -kV + (2αλ(Γ)V +υ maxIσΔ(t)II2+υz ). kt So, property V∈M+for V has the form Ve ≤-kVe+2αλl(Γ)VN + 1 (υP maxIσΔ(t)II2+υz ). Appendix F. Proof of Theorem 5 Consider Lyapunov function V(t)=Ve(t)+0.5γε-1µ2(t)=Ve(t)+Vµ(t). Write V as Apply the proof scheme of theorems 1, 2 and obtain V<-kVe +1 [amax]|Д.(t)||2 + ®] , (F.1) where maxh2(t) < to, to — 0 is some number. The inequality (38) follows from (F.1). Appendix H. Proof of Theorem 6 Show boundedness of system ASED trajectories. Let such number p лexists that the equality hд (t) = p*,.sN (t) is true. Consider Lyapunov function V (t) = Ve (t) + V^N (t) + V. (t) = 0.5e2(t) + 0.5yN (Sp.(t))2 + 0.5^2 (t |Г V (t), where Sp. = PN - p* .. Write V as V ke + eДNPH+eS/djNSN eSpN^N eДnPh . (H.1) Therefore, we have V< -2kVe. Integrate this inequality and obtain V (t) < V(10) - 2kjVe(t)dT . (H.2) t0 Hence, all trajectories of the system ASED belong area Q = {(e, Д.,SpN): V(t) < V(10)} . Consider Lyapunov functions V(t) and Vpn (t) = 0.5 (dpN(t))2. Transform V to the form Ve = - ke2 + e Д TNPH + eSpN^N. (H.3) The vector P has property PE . Apply the proof scheme of lemma 1 and ensure for Ve property Ve e M+ in the form Ve = -ke2+eДNPH + eSPNsN < - kVe+ a max 1ДN I1 +^VN ■ where s2 < dN, dN — 0 is some number. Ensure the condition V^ e M+. By analogy with (H.4) obtain V Pn = -YNeSPNSN = -U(/NSPNSN + e2 ) = f 1 ^ 2 - UI e + - YNeSPNSN I + UYNeSpNgN - oyNspN,sN + UyNspNsN < (H.5) < — °YnSPn sN + uYn \e5tNSNM | < - -udNYNVPN+ uVe. As и does not influence on properties of the system assume и = 1 . So, we have for Ve and V^ following inequalities Ve V pN - k и 2dN k дUdNYN V PN ] (H.6) a max ||Дn|I2 Let S = [s s 1 , e, pN L e PN ] A = -k 2dN k , F = a max 1д.1 Pn 3 ’ PN u -- UdNYN _ 0 ] Let such functions sp (t) > 0 exist that VP(t) <Sp(t) V(t > t0)&(Vp (t0)<sp (t0)) , p = e, Pn . We obtain the vector system of comparison for (H.6) Se,Pn (t) = ApNSe,д. (t) + FpN - (H.7) Stability conditions of the system (H.7) have the form 228 k > 0 , k dNY. — dN . Hence t V(t) < eAPN(t-t0)Se,PN (10) + JeAPN(t-T)Fpn (t)dT . t0 Limiting properties the ASED -system estimate as V(t) ≤ k mtax IIΔN2Σ1,µ(t)t→∞, where Σ (t) is the first column of the matrix t ∫eAV(t-τ)dτ. t0VIII. Results of Modeling
IX. Conclusion
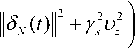
Appendix C. Proof of Theorem 3
Appendix D. Proof of Lemma 1
Appendix E. Proof of Lemma 2
- ke2 + |e| |ДNPH + Зд,^| <
- ke2+1 [||Д ,| П IP,111 * )2s. ]< <H.4)
Список литературы Adaptive Observers for Linear Time-Varying Dynamic Objects with Uncertainty Estimation
- R. L. Carrol, D. P. Lindorff, "An adaptive observer for single-input single-output linear systems," IEEE Trans. Automat. Control, 1973, vol. AC-18, no. 5, pp. 428–435.
- R. L. Carrol, R. V. Monopoli, "Model reference adaptive control estimation and identification using only and output signals," In Processings of IFAC 6th Word congress. Bos-ton, Cembridge, 1975, part 1, pp. 58.3/1-58.3/10.
- G. Kreisselmeier, "A robust indirect adaptive control ap-proach," Int. J. Control, 1986, vol. 43, no. 1, pp. 161–175.
- P. Kudva, K. S.Narendra, "Synthesis of a adaptive ob-server using Lyapunov direct method," Jnt. J. Control, 1973, vol. 18, no. 4, pp. 1201–1216.
- K. S. Narendra, P. Kudva, "Stable adaptive schemes for system: identification and control," IEEE Trans. on Syst., Man and Cybern, 1974, vol. SMC-4, no. 6, pp. 542–560.
- S. Nuyan, R. L. Carrol, "Minimal order arbitrarily fast adaptive observer and identifies," IEEE Trans. Automat. Control, 1979, vol. AC-24, no. 2, pp. 496–499.
- M. J. Feiler, K. S. Narendra, "Simultaneous identification and control of time–varying systems," In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego CA, U.S.A., 2006, pp. 1-7.
- N. Jing, Y. Juan, R. Xuemei and Gu. Yu, "Robust adaptive estimation of nonlinear system with time-varying pa-rameters," International journal of adaptive control and signal processing, 2014, vol. 29, no. 8, pp. 1055–1072.
- G. Bastin, and M. R. Gevers, "Stable adaptive observers for nonlinear time-varying systems. IEEE Trans. Automat. Control, vol. AC-33, no. 7, 1988, pp. 650-658.
- Y. Zhang, B. Fidan, and P.A. Ioannou, "Backstepping control of linear time-varying systems with known and unknown parameters," IEEE Trans. Automat. Contr., 2003, vol. AC-38, no. 11, pp. 1908–1925.
- Q. Zhang, and A. Clavel, "Adaptive observer with expo-nential forgetting factor for linear time varying systems," In Proceedings of the 40th IEEE Conference on Decision and Control (CDC ’01), 2001, vol. 4, pp. 3886–3891.
- V.Ja. Katkovnik, V.Е. Heysin, "Adaptive control static essentially time-varying object," Automation and Remote Control, 1988, vol. 49, no. 4, pp. 465–474.
- I. I. Perel'man, "Methods for sound estimation of linear dynamic plant parameters and feasibility of their imple-mentation on finite samples," Automation and Remote Control, 1981, vol.42, no. 3, pp. 309–313.
- D. Bestle, M. Zeitz, "Canonical form observer design for nonlinear time-variable systems," Int. J. Control, 1983. vol. 38, no. 2, pp. 419–431.
- N.N. Karabutov, Adaptive identification of systems: in-formation synthesis. Moscow: URSS, 2007.
- N.N. Karabutov, "Methods of -algorithms control," In Mathematical models of non-linear phenomena, processes, and systems: from molecular scale to planetary atmos-phere, Ed. Alexey B. Nadykto, Ludmila Uvarova, Anatolii V. Latyshev. Nova Science Publishers Inc, 2013, pp. 359-396.
- N.N. Karabutov, "Construction of adaptive observers of time-varying objects with specified quality of adaptation," In Microprocessor systems of automation: Theses of re-ports of II All-Union scientific and technical conference. Novosibirsk, 1990, pp. 10-11.
- N.N. Karabutov, "Influence of measurement information on the properties of adaptive systems," Measurement Techniques, 2010, vol. 53, no. 9, pp. 956-963.
- F.R. Gantmacher, The Theory of Matrices. AMS Chelsea Publishing: Reprinted by American Mathematical Society, 2000.
- P. V. Pakshin, "Exponential dissipativeness of the random-structure diffusion processes and problems of robust stabi-lization," Automation and Remote Control, 2007, vol. 68, is. 10, pp. 1852–1870.
- E.A. Barbashin, Lyapunov function. Moscow: Nauka, 1970.


