Адаптивное устройство для защиты от дуговых разрядов при электроэрозионной обработке

Электроэрозионная обработка (ЭЭО) широко применяется в машиностроении для получения отверстий и фасонных полостей в заготовках из токопроводящих материалов. Условием стабильного и производительного процесса является равномерное распределение электрических разрядов по обрабатываемой поверхности. Однако при затрудненной эвакуации продуктов эрозии это условие обычно нарушается, и могут возникать «аномальные» дуговые разряды, приводящие к появлению шлаковых наростов на электродах. Поэтому защита от дуговых разрядов является одной из задач управления процессом ЭЭО [I].

Для решения этой задачи целесообразно использовать устройства для защиты от межэлектродных коротких замыканий (МКЗ), которые контролируют мгновенное значение напряжения на промежутке. При выборе порога срабатывания выше напряжения «аномального» разряда такое устройство позволяет прервать дуговой импульс в начальной стадии и, тем самым, снизить вероятность наростообразования. Но при этом возможны и ложные отключения генератора импульсов из-за случайного разброса напряжения на дуге разряда.

В [2] показано, что параметры устройства следует выбирать с учетом характеристик распределения МКЗ по длительности и ограничений по величине порогового напряжения срабатывания С_пор. Верхняя граница порогового напряжения соответствует напряжению на межэлектродном промежутке (МЭП) в конце разряда м, _к, а его нижняя граница определяется напряжением дугового (аномального) импульса и временем задержки срабатывания /_зс. Средние значения этих напряжений зависят от длительности импульсов, свойств рабочей жидкости и материалов электродов [1]. Поэтому для хорошей работы устройства необходимо изменять величину U_nop при изменении режима и условий обработки.

При малом числе варьируемых параметров такая задача может быть решена путем программного управления. Однако при широкой номенклатуре материалов и большом количестве режимов более удобным является задание порогового напряжения с помощью встроенного измерителя напряжения на дуге разряда.

На рис. 1 изображена функциональная схема системы автоподстройки порогового напряжения [/пор.

Питание межэлектродного промежутка МЭП осуществляется от генератора импульсов ГИ, в состав которого входят задающий генератор ЗГ, логический элемент И и транзисторные силовые блоки СБ. В системе используется быстродействующее устройство для зашиты от коротких замыканий УЗК, на входы которого подаются задающие импульсы х_зг и напряжение МЭП u_s(t) [3]. Порог срабатывания устройства задается с помощью следящей измерительной системы ИС, состоящей из компараторов К1,... КЗ, логического устройства ЛУ, реверсивного счетчика РСч и цифро-аналогового преобразователя ЦАП:

(О где С^Ц) - выходное напряжение ЦАП; кс - коэффициент связи.

Рис. 1. Функциональная схема системы автоподстройки

Логические сигналы на выходах компараторов х,= 1 (/=1,... 3) возникают при u^t'y>U_n причем U_x > U₂> U₃. С помощью напряжений Ц и U₃ задаются границы настройки и выявляются импульсы холостого хода и короткого замыкания, которые не должны создавать счетных импульсов для РСч.

Формирование импульсов сложения у, или вычитания у₂ на выходах ЛУ (рис. 2) происходит в моменты окончания импульса ЭДС генератора х_Е = х_зг ■ х_узк и описывается функциями

• У] = Xj ■ х₂ ■ х₃ • dx_E ; у₂ = х_х ■ х₂ ■ х₃ • dx_E,

где х_узк - выходной сигнал УЗК; dx_E - импульсный сигнал, соответствующий заднему фронту⁷ импульса х_Е.

Такая логика обеспечивает контроль напряжения на МЭП в конце разряда и его использование в качестве задающего воздействия для контура настройки напряжения U_nop.

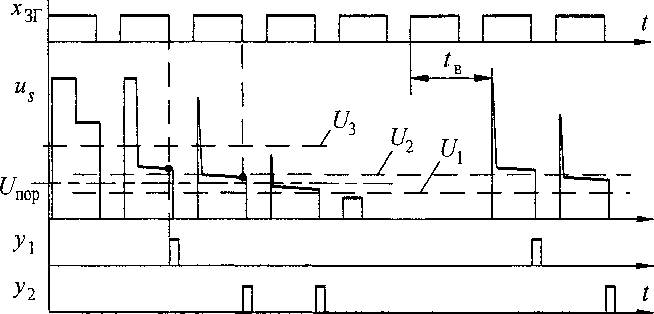
Рис. 2. Диаграмма работы логического устройства

Рассмотрим работу следящей системы с учетом влияния УЗК. Обозначим через u_{s к} случайную величину - напряжение на МЭП в конце импульса, м₂(0 ~ случайный процесс на выходе ЦАП, /(и) - плотность вероятности величины u_SK для всех импульсов, включая холостые и импульсы короткого замыкания. Точками u=U_x nu=U₃ возможные значения напряжения делятся на три интервала, которым соответствуют участки кривой распределения/ь/₂, и/₃, (рис. 3).

Вероятности попадания величины uJK в эти интервалы обозначим через \, \, и \, причем X) + Х2 + Х3 = 1. Вероятность пробоя МЭП л=рКк <из^ = лх + л2

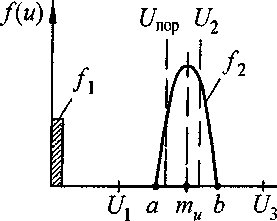
Рис. 3. Плотность распределения напряжения импульсов

Предположим, что на интервале [а, £], соответствующем разрядам, плотность вероятности может быть описана уравнением параболы в виде

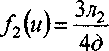
₁ (и-mJ² д²

4d L

где m_u=(a + b)/2 - математическое ожидание контролируемого напряжения для разрядов; 3 = т_и - a = (b - а)/2, v = (и - т„ ^(8.

интегральная функция распределения величины м$к в интервале [C/i, Е73] будет иметь вид:

при U_х< и < a; при a < и < b ; при b < и < U₃.

л1.

F^ = - л_х -vVil^y 3v-v³ +2 ,

Лу 4“ Л 2,

Поскольку выходное напряжение ЦАП изменяется дискретно, а вероятности появления сигналов у_х, ^2, определяющие направление счета, зависят от его текущего значения, случайный процесс м₂0 представляет собой Марковскую цепь с матрицей переходных вероятностей [Лу]. Число состояний этой цепи (£+1) равно числу возможных значений напряжения.

Определим характеристики стационарного случайного процесса, предполагая, что при выбранном шаге квантования h напряжение не выходит за пределы интервала [а, 6]. В этом случае наибольший номер состояния Марковской цепи равен k = (b-a^jh, и некоторому состоянию S, можно поставить в соответствие уровень напряжения

U_2i = a + h-i, i = 0,к . ' (5)

Согласно рис. 3 и уравнениям ЛУ при х_узк = 1 импульсы на входе сложения РСч возникают с вероятностью р,. = X - F\U_2] ), а на входе вычитания - с вероятностью q_t = F^U 2/)-А ■ Вероятность отсутствия этих двух импульсов и сохранения состояния S, равна г = 1 - л + л_х = 1 - л₂. Следовательно, элементы матрицы перехода могут быть описаны общей формулой:

q_t, если7 = z-l;

г, если j = i;

р_х, если 7" = / + !;

О, в стальных случаях.

Технология

Как известно, такая матрица соответствует процессу одномерного случайного блуждания [4, 5 ]. Финальные вероятности {РД, Z = 0, £ состояний процесса вычисляются путем последовательного решения уравнений вида

Д =A_i^_i+^ + ?i+i^+i, которые дополняются условием р0 = 1 - г и условием нормировки У^ Д -1. В результате получаем:

^^ЕЙ—; ^=ро-П—’                      <7> i=l к=0 Чк*\            к=0 Як+1

Заметим, что отношение р_к,Ч_к+\ и, соответственно, финальные вероятности не зависят от величин ли Л;.

С помощью финальных вероятностей можно оценить точность настройки порогового напряжения. Для этого найдем вероятность нахождения величины ы₂(0 ^в заданной полосе значений (m^nh);

P(nh)-P ^u2(t)-m^< ик], п = 0, 1,...

Возьмем нечетное число состояний (£+1), при котором средний уровень напряжения Un, I = к/2 совпадает с математическим ожиданием напряжения разрядов т_и. Тогда получим:

/+и

PW = £д,и = 0,1,...                                                <8> i=l-n

В табл. 1 приведены значения этой вероятности, рассчитанные по формулам (3)...(8) при а=24 В, ш„=25 В для двух значений шага квантования: /г=0,1 В и Л=0,05 В. Как видим, при шаге /г=0,05 В напряжение м20 не выходит за пределы 25+0,5 В с вероятностью 0,99997.

Таблица 1

Вероятность нахождения напряжения ЦАП в интервале т _u±nh

Отклонение и И, В	0	од	0,2	0,3	0,4	0,5
Вероятность Р (и ■ 0,1)	0,213	0,582	0,825	0,944	0,987	0,998
Вероятность Р(п ■ 0,05)	0,152	0,664	0,918	0,9885	0,99914	0,99997

Следует отметить, что ввиду случайных изменений напряжения разряда возможны ложные отключения ГИ при нормальном импульсе напряжения. Вероятность такого события определяется соотношением

Рл~Р Va^SK

Так как это событие может происходить при разных значениях порогового напряжения Цюрг” ^с £Дц Для нахождения величины р_а воспользуемся формулой полной вероятности. Получим:

1=1

Расчетные значения вероятностир_л приведены в табл. 2 для а = 24 В, ш„=25 В, 2= 1, Я] = 0.

Полученные результаты показывают, что снижение шага квантования h и коэффициента к_с приводит к уменьшению вероятности ложного отключения генератора.

Для выбора этих параметров зададимся допустимой долей потерь рабочего времени А / _раб, временем восстановления импульсов после МКЗ t_B (рис. 2) и частотой задающего генератора/_зг

• [2]. По этим параметрам найдем среднюю частоту срабатывания УЗК /_к = Д/рабД, . Очевидно, что должно выполняться условие р_а< /_к/ /_зг . Например, при/_к= 0,1 Гци/_зг=100кГц получаем р_л< 1-Ю^-6, что в табл. 2 соответствует коэффициенту ^_с=0,94 при шаге квантования Л = 0,05 В.

Таблица 2

Вероятность ложного отключения генератора

Шаг квантования h, В	0,05			0,1
Коэффициент кс	0,94	0,95	0,96	0,94	0,95	0,96
Вероятность рП	ЬЮ"8	6-Ю-5	6-10”3	5-Ю-6	6-Ю-4	МО-2

В реальных условиях обработки наблюдается последействие разрядов, и напряжение на МЭП изменяется не так быстро, как при абсолютно случайном процессе. Вследствие этого интервал распределения [а, 6] на небольшом отрезке времени может оказаться более узким по сравнению с принятым в расчете (2 В). При этом математическое ожидание т_и изменяется при изменении межэлектродного зазора и загрязненности рабочей среды.

Время выхода следящей измерительной системы на установившийся режим (время настройки) зависит от начального значения напряжения ЦАП О^_нач, частоты импульсов /_зг, шага квантования h и вероятности возникновения разрядов X'

• ^— ^2 нач

  / >1--------------1.

Например, при \т_и — Г7_2нач[ =2 В,/_зг=1000 Гц, Л=0,05 В и Х=1 получаем t_H « 4Q/f_3V =0,04 с (при отсутствии срабатываний УЗК).

Моделирование работы системы с помощью программы VisSim показало, что предлагаемый способ автоматической настройки УЗК с помощью следящей измерительной системы работоспособен и при достаточно малом шаге квантования позволяет поддерживать стабильное значение порогового напряжения.

Экспериментальная проверка предлагаемого устройства производилась при прошивке квадратного отверстия площадью 1 см² графитовым электродом-инструментом в стальной заготовке. Обработка велась прямоугольными импульсами с частотой 1 кГц, скважностью 1,2 и амплитудой тока 60 А при t7_nOp= 23,5...25 В, шаге квантования Л=0,05 В и времени задержки срабатывания t_3C= 200 мкс. Для очистки МЭП применялась автоматическая релаксация (периодический отвод) электрода-инструмента. В результате глубина обработки 10 мм была достигнута за 20 мин, а глубина 20 мм - за 60 мин.

Таким образом, применение автоматической настройки порогового напряжения и малого времени задержки срабатывания защиты позволяет снизить вероятность наростообразования в МЭП.