Адаптивный фильтр сигнала датчика ускорения

DOI:

При проведении любых измерений всегда возникает проблема отделения полезного сигнала от шума или помехи. Разделение мешающего сигнала на два типа — шум и помеха, как правило, весьма условно. Мы можем считать, что шум возникает в электрических цепях как результат ее работы, например, дробовой шум, обусловленный дискретным характером потока заряженных частиц или потоком фотонов. Помеха, как правило, обусловлена внешним воздействием на датчик. Можно считать, что подобным воздействием являются вибрации [2], создаваемые винтомоторной группой летательного аппарата мультироторного типа, существенно искажающие результаты измерения датчиком компонент ускорения.

Универсальных решений по борьбе с помехами или шумами не существует. Выбор того или иного фильтра для выделения полезной составляющей сигнала, как правило, определяется типом и источником помехи или шума, физическими процессами, определяющими появление и распространение мешающих сигналов. В настоящее время при цифровой обработке сигналов широко применяются фильтры, использующие медианное сглаживание, скользящее среднее, метод Савицкого — Голея, различные линейные алгоритмы [3–5].

Наибольшее распространение при обработке сигнала с датчика ускорения получил фильтр Калмана [7], в основе которого лежит авторегрессионная модель. Фильтр Калмана позволяет получить хорошие результаты, но требует больших вычислительных мощностей в сравнении с остальными методами. Вместе с тем априорная информация о помехе позволяет существенно уменьшить объем вычислений при сохранении качества выделения полезного сигнала. В качестве источника такой информации может выступать акустический сигнал, который, очевидно, коррелирован с вибрациями, создаваемыми винтомоторной группой. Более того, можно считать, что источником акустического сигнала являются вибрации.

Отметим, что датчик ускорения используется для измерения постоянных или сравнительно медленно изменяющихся значений ускорения, обусловленных эволюциями беспилотного аппарата. Так как для измерения звука, коррелированного с помехой, используется микрофон, то полученный сигнал будет ограничен по частоте снизу примерно на уровне 10 Гц из-за конструктивных особенностей микрофонов, то есть сигнал с микрофона не будет содержать данных об ускорении аппарата, а только о помехе. Указанные факты можно использовать для построения адаптивного фильтра.

1.    Описание адаптивного фильтра

На рисунке 1 представлена возможная структурная схема устройства, выполняющая измерение компоненты ускорения с учетом воздействия помехи. На вход системы поступает последовательность отсчетов измеряемого сигнала s (к) с шумом п (к), обусловленным погрешностью квантования и работой электронной схемы. На полезный сигнал накладывается помеха п (к), взаимодействие которой с датчиком моделируется блоком с импульсной характеристикой w (к). Сформированный таким образом сигнал д (к) складывается с полезным, результат s (к) + п (к) + д (к) является моделью сигнала с датчика, измеряющего ускорение. Измеренный сигнал помехи п (к) поступает на вход адаптивного фильтра, выходной сигнал которого у (к) вычитается из измеренного.

Таким образом,

е (к) = s (к) + n (к) + g (к) - у (к) - К (к) ,

здесь К (к) — погрешность измерения помехи. Полученный выходной сигнал также является сигналом ошибки, используемым для корректировки отсчетов коэффициентов адаптивного фильтра.

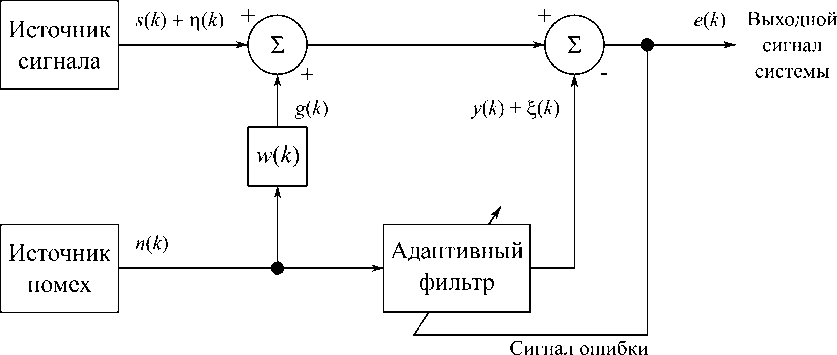
Рис. 1. Структурная схема адаптивного фильтра

Полагая, что коррелированы только сигналы g (к), п (к) и у (к) получим выражение для математического ожидания квадрата ошибки

М { е ² (fc) } = М { s ² (к) } + М { [д (к) - у (к)] ² } + М { [ _п (к) - К (к)] ² } .      (2)

Отсчеты сигнала с выхода адаптивного фильтра связаны с сигналом помехи следующим соотношением

N - 1

у (к) = ^ h ( ⁱ )n (к - 1) = H T n (к) ,                      (3)

i=0

где n ^T (к) = [п (к), п (к - 1), ..., п (к - N - 1)] — отсчеты входного сигнала; H T (п) = = [h ₀ , h 1 , ..., h _N -1 ] — отсчеты импульсной характеристики адаптивного фильтра (весовой вектор). Тогда соотношение (2) запишется в виде

М { е ² (к) } = М { s ² (к) } + М {[ д (к) - H T n (к) ] ² } + М { [n (к) - К (к)] ² } .   (4)

Это выражение описывает стандартную поверхность квадратичной ошибки с одним единственным минимумом.

Найдем значения отсчетов импульсной характеристики, обеспечивающие минимум математического ожидания квадрата ошибки. Для этого вычислим градиент от выражения (4) и, прировняв его к нулю, получим

^{М {} д ^(к) n ^{T (к)}} = ^{М { H}T, t n ^(к) n ^{T (к)}} .

Полагая, что весовой вектор и вектор сигнала не коррелированы, запишем

^М { д ^(к) n ^{T (к)}} = ^{н T} _Pt ^М { n ^(к) n ^{T (к)}} .                     ⁽⁵⁾

Форма полученного выражения совпадает с известным [1], вводя аналогичные обозначения

P = M {g (к) n (к)} , взаимная корреляция между входным сигналом и оцениваемым параметром,

R = M {n (к) nT (к)} , автокорреляционная матрица входной сигнальной последовательности. В результате соотношение (5) запишется в виде:

P T = H T _pf R .

Это уравнение является общеизвестным уравнением Винера — Хопфа [1], которое дает оптимальное (по методу наименьших квадратов) винеровское решение для H _opt :

H _opf = R - 1 P .                                 (6)

В общем случае использование решения (6) для нахождения вектора оптимальных коэффициентов фильтра требует знания всех отсчетов входных сигналов, что, очевидно, не всегда возможно. Поэтому найдем выражение для итерационного процесса определения весового вектора. Выполняя действия, подобные приведенным в работе [6], перепишем выражение для ошибки (1), используя соотношение (3), получим:

е (к) = s (к) + п (к) + g (к) — H T n (к) — ^ (к).                    (7)

В этом случае математическое ожидание квадрата ошибки будет иметь вид (здесь как и прежде полагаем, что коррелированы только сигналы g (к), п (к) и у (к)):

M { е ² (к) } = M { s ² (к) } +M { g ² (к) } — 2 P T H + H T RH + M { п 2 (к) } +M { ^ 2 (к) } .

Вычислим градиент от математического ожидания

V = — 2 P + 2 RH .

Умножив последнее выражение на R - 1 /2 слева, в результате будем иметь:

- 1

—V = — R - 1 P + H .

Используя оптимальное винеровское решение (6), получим выражение для нахождения вектора коэффициентов фильтра за один шаг:

H _opf = H — R^ V .

Можно показать [1], что к полученному решению асимптотически сходится следующий итерационный процесс:

H ,+i = H — ^ V , ,                          (8)

здесь индекс к означает, что градиент вычисляется на шаге к, когда вектор весовых коэффициентов равен H , , ^ — параметр сходимости.

Найдем оценку для градиента, входящего в выражение (8), используя соотношение (7):

V k =

де2 (к) dho де2(к) dh N

= 2e (k)

/ де ( к)\ dh o

. . . де ( к ) dh у

•

— 2e (k) n (k)

Окончательно алгоритм нахождения оптимального вектора коэффициентов примет вид:

H k+i = H k + 2^e (k) n (k).

2.    Результаты моделирования

При проведении моделирования адаптивного фильтра в качестве полезных данных s (k) использовался сигнал, представляющий собой последовательность треугольных импульсов с нулевым средним (отсутствует постоянная составляющая сигнала), имеющий широкий спектр. При этом средняя мощность полезного сигнала примерно составляла 0,13. В качестве помехи п (k) был выбран гаусовский шум также с нулевым средним и дисперсией, равной 0,5. Таким образом, отношение сигнал — шум составило примерно — 2, 8 Дб. В соответствии со структурной схемой устройства (рис. 1), перед добавлением помехи к сигналу она была пропущена через фильтр низких частот первого порядка. Адаптивный фильтр имел всего восемь весов импульсной характеристики, то есть для вычисления нового выходного отсчета требуется выполнить восемь операций сложения и умножения.

На рисунке 2 представлен пример вычисления выходного сигнала системы, хорошо виден процесс адаптации весовых коэффициентов фильтра к оптимальным значениям, при этом среднеквадратичное значение относительной ошибки измерения меньше 0,1 после окончания адаптации. Зависимость значения величины ошибки определения весовых коэффициентов фильтра от номера итерации приведена на рисунке 3. Здесь под ошибкой понимается среднее арифметическое значение квадрата отклонения рассчитанных значений весовых коэффициентов от известных значений. Обучающая кривая усреднена по восьми реализациям.

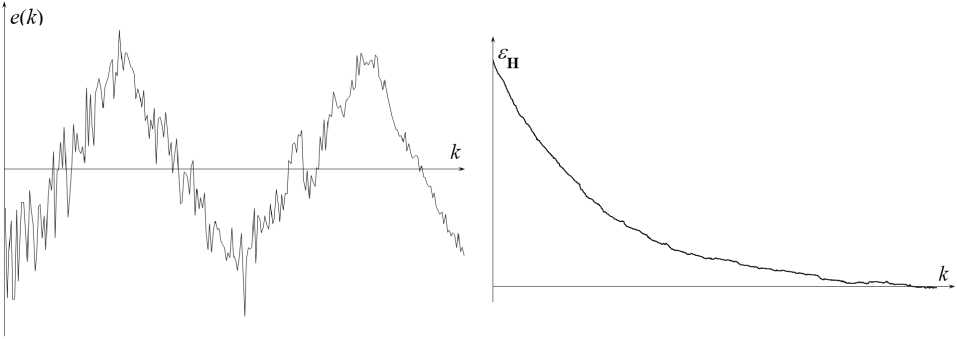
Рис. 2. Выходной сигнал системы

Рис. 3. Обучающая кривая

Заключение

Таким образом, разработанный адаптивный фильтр позволяет на основе априорных данных о внешней помехе существенно улучшить точность измерения полезного сигнала. Как уже упоминалось, в качестве дополнительной информации можно использовать оцифрованный акустический сигнал, создаваемый вибрациями винтомоторной группой летательного аппарата мультироторного типа. Использование предложенного алгоритма при этом существенно сокращает объем вычислений. В работе показано, что достаточно использования восьми весовых коэффициентов фильтра, чтобы относительная ошибка определения измеряемой величины не превосходила 10 %.