Адаптивный итеративный алгоритм для синтеза фокусаторов
Автор: Котляр В.В., Никольский И.В., Сойфер В.А.
Журнал: Компьютерная оптика @computer-optics
Рубрика: Численные методы компьютерной оптики
Статья в выпуске: 12, 1992 года.
Бесплатный доступ
Предложен новый адаптивный вариант итеративного алгоритма Герчберга-Секстона применительно к задаче синтеза фокусаторов. Показано, что применение некоторой подстраивающей процедуры на каждом шаге итераций позволяет существенно уменьшить отклонение получающегося распределения интенсивности света в области фокусировки от заданного распределения, без существенного уменьшения энергетической эффективности.
Короткий адрес: https://sciup.org/14058264
IDR: 14058264
Текст научной статьи Адаптивный итеративный алгоритм для синтеза фокусаторов
Известный итеративный алгоритм Герчберга-Секстона [1] имеет целый ряд интересных приложений для решения задач анализа и синтеза когерентных световых полей.
Так в работе [2] алгоритм Герчберга-Секстона (ГС) использовался для расчета фазового профиля одномерной дифракционной решетки, мультиплицирующей излучение на произвольное число порядков дифракции с заданным распределением энергии по ним. В [3] использовался алгоритм ГС для расчета фазовой функции элементов плоской оптики, фокусирующих когерентное излучение в заданную область пространства с заданным распределением энергии в этой области.
В данной работе предложен и исследуется новый вариант итеративного алгоритма ГС применительно к задачам синтеза фокусаторов. Показано, что применение некоторой адаптивной подстраивающей процедуры на каждом шаге итеративного процесса позволяет существенно сократить среднеквадратичное отклонение полученного распределения интенсивности от заданного. При этом "плата” за точность в виде потерь энергии, попадающей в область фокусировки, составляет не более 20%.
АДАПТИВНЫЙ АЛГОРИТМ
Рассмотрим классический вариант алгоритма ГС применительно к расчету фазовой функции пропускания оптического элемента, фокусирующего когерентное излучение в отрезок прямой с равномерным распределением энергии (интенсивности) вдоль отрезка. На каждом шаге итеративного процесса полученное распределение интенсивности 1П(Е) в частотной плоскости заменяется на требуемое распределение согласно замене
A, Ее [ерЕ2] о, Е$ Кр£2Ь
Распределение интенсивности в области фокусировки представляет собой квадрат модуля преобразования Фурье от фазовой функции пропускания оптического элемента равной
f(x) =
Вехр(^(х)), х е [хрх2]
, х ? [Xj,x2],
где А, В - постоянные. Поэтому интенсивность 1П(Е) должна являться аналитической функцией, имеющей вполне определенные минимальный период модуляции и максимальную величину первой производной. Требование скачкообразного поведения интенсивности (1) в зоне фокусировки и равенства нулю ее вне зоны фокусировки снижает скорость сходимости алгоритма ГС и может приводить к расходимости.
Поэтому не хотелось бы сильно искажать аналитический (плавный) характер распределения интенсивности в Фурье-плоскости и, в то же время, применить некоторую подстраивающую процедуру на каждом шаге, чтобы увеличить скорость сходимости и уменьшить ошибку отклонения полученного распределения интенсивности от требу емого.
Предлагается следующая процедура подстройки. На п шаге итераций в Фурье-плоскости полученная функция интенсивности 1П(Е) заменяется на функцию 1П(Е) равную
«П«) =
W
2^2 - 1„(Е). Е е [ЕР Е21
1„(Е)
, Е $ (ЕР Е2).
где Wn, Wn - энергия света на всей оси Е и в отрезке [Ер Е21, соответственно.
Замена (3), как видно, оставляет без изменения полученную на n-м шаге функцию 1п(|) вне отрезка фокусировки и видоизменяет ее только в отрезке [|j, ?2]. Причем таким образом, что почти не меняет гладкости полученной функции. Замена же заключается в адаптивном выравнивании полученного распределения интенсивности: значения функции 1ПЙ), превышающие средний уровень, становятся на столько же (или с некоторым коэффициентом) ниже среднего, и наоборот, значения интенсивности, которые ниже среднего, становятся на столько же выше.
Наиболее оптимальным оказалось совместное применение алгоритмов ГС и адаптивного, то есть замен (1) и (3). Поскольку в алгоритме (1) быстро, всего за несколько итераций, почти вся энергия света собирается в заданном отрезке фокусировки, то предлагается начинать итеративный поиск фазовой функции фокусатора с алгоритма ГС, а через несколько итераций, например, когда отношение Wn/Wn станет близко к единице, продолжить далее итеративный процесс с адаптивной процедурой (3).
ЧИСЛЕННЫЕ РЕЗУЛЬТАТЫ
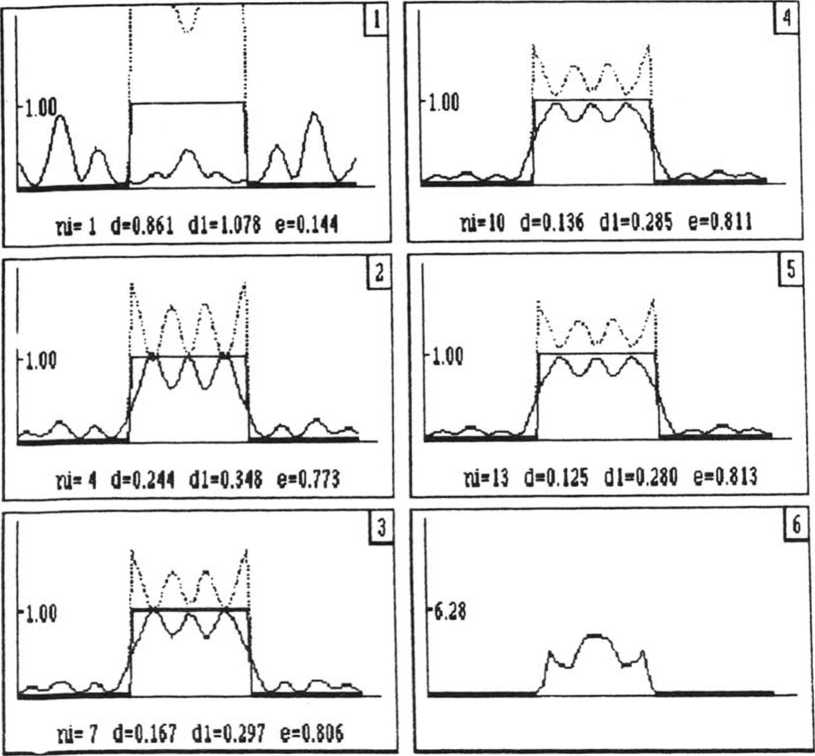
Сравнение алгоритма ГС и его адаптивной модернизации проводилось численно с использованием алгоритма быстрого преобразования Фурье. На рис. 1 показаны результаты работы алгоритма ГС с заменой (1). На рис. 1.1— 1.5 показаны распределения интенсивности в частотной плоскости 1п(£) для итераций с номерами п = 1,4, 7,10,13, соответственно, и на рис. 1.6 показана фаза ф13 (х) фокусатора, формирующего в Фурье-плоскости распределение интенсивности 113(х). При этом: N = 128 - общее число отсчетов, 2N] = 16 - число отсчетов на фокусаторе, 2М = = 32 - число отсчетов в области фокусировки, то есть отрезок из (1) равен [^, $2 ] = [~16Н, 16Н], где Н — диск-

■IX
№ 1 d-0.861 dl-1.078 e-il«
11=128 ni=e 8=16 Hi=13 №=1
Hf=l
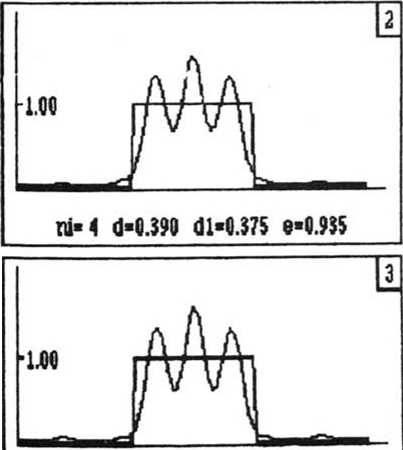
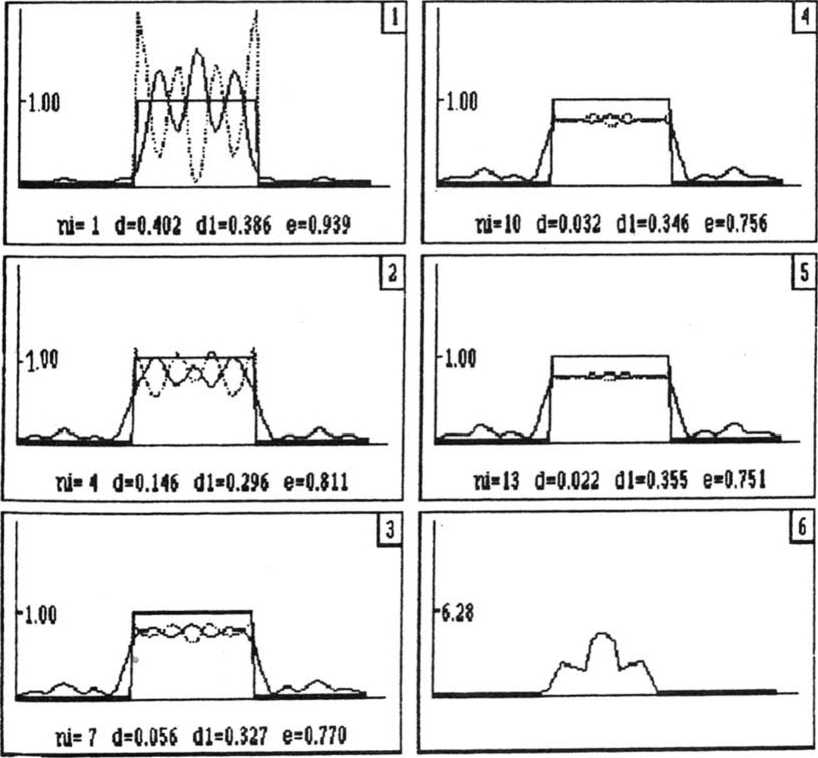
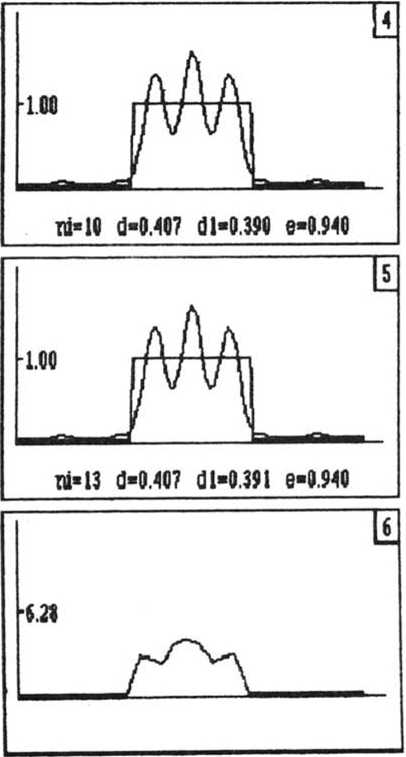
№7 Рис. 1. Результаты применения алгоритма ГС для синтеза фокусатора в отрезок: 1 - 5 - распределения интенсивности В ПЛОСКОСТИ фокусировки, 6 - полученная фаза фокусатора на 13 шаге ретность в частотной плоскости, А = 1, N1 = 13 - общее число итераций. Начальное распределение фазы на фокусато-ре выбиралось чисто случайным с дисперсией равной 2я. Из рис. 1 видно, что при рассматриваемых параметрах фокусировка преобразуется в отрезок, равный двум диаметрам минимального дифракционного пятна. Видно также,что за 13 итераций среднеквадратичная ошибка d отклонения полученного распределения интенсивности от требуемого равномерного распределения в отрезок [Jp $2] составляет 41% и энергия W)3, заключенная в отрезке [{р {21- составляет 94% от полной энергии W|3, то есть е=^— = 0,94 (см. рис. 1.5). W13 На рис. 2 показаны результаты работы адаптивного алгоритма с заменой (3). На рис. 2.1—2.5 показаны полученные распределения интенсивности в частотной плоскости In[$J Для итераций с номерами n = 1,4, 7, 10, 13. и на рис. 2.6 показана фаза Ф13(х). Остальные параметры, относящиеся к рис. 2, такие же как в предыдущем случае. Пунктиром на рис. 2.1-2.5 показаны требуемые распределения интенсивности Тп(!-) из (3) для соответствующих номеров итераций. Из рис. 2.5 видно, что за 13 итераций среднеквадратичная ошибка d отклонения полученной интенсивности от требуемой (равномерной) составила 13% и отношение энергий равнялось е = 81%. Из сравнения рис. 1 и рис. 2 видно, что применение адаптивной процедуры подстройки в алгоритме ГС приводит к уменьшению ошибки почти в 4 раза, а энергетическая эффективность, то есть часть энергии света, попадающая в заданный отрезок, уменьшается всего на 13%. Рис. 2. Результаты применения адаптивного алгоритма для синтеза фокусатора в отрезок: М=128 И1=8 М=16 MU13 Uar=3 Mf=1 Af -6.3800 Sc:d.5000 Sb-8.M 1-S - распределения интенсивности в плоскости фокусировки, сплошные линии - полученная интенсивность, пунктирные линии - требуемая интенсивность, 6 - полученная фаза фокусатора на 13 шаге На рис. 3 показаны результаты совместной работы двух алгоритмов. Первые 5 итераций были проведены с помощью замены (1) (они не показаны на рис. 3), а последующие 13 итераций были проведены с помощью замены (3). На рис. 3.1—3.5 показаны полученные интенсивности 1п[?] в частотной плоскости для номеров итераций п = 6, 9, 12, 15, 18, и на рис. 3.6 показана фаза фокусатора ^^ (х). Пунктиром показаны требуемые распределения интенсивности 1П[£] для соответствующих номеров итераций. Остальные параметры, относящиеся к рис. 3, те же, что и ранее. Из рис. 3 видно, что совместное применение алгоритма ГС и адаптивного алгоритма приводит к существенному уменьшению ошибки d (за 15 итераций ошибка уменьшилась до 3%, рис. 3.4) и при этом энергетическая эффективность осталась на высоком уровне - 76%. Рис. 3. Результаты применения совместно алгоритма ГС и адаптивного: 1 -5 - интенсивность в плоскости фокусировки, сплошные линии - полученная интенсивность, пунктирные - требуемая интенсивность, 6 - полученная фаза на 18 шаге H=12fi М1=8 М=1Ь ики Uar=3 Hf=2 Af=l.B№0 Sc=1.5000 Sb =0.0000 Заметим в заключение, что продолжение итераций в ситуации, применительной к рис. 1, приводило к слабому росту отклонения d, а в случае, относящемуся к рис. 3, продолжение итераций приводило к дальнейшему уменьшению ошибки.