Адаптивный модуль как эффективное средство обучения математике первокурсников с разным уровнем школьной математической подготовки

DOI:

Некоторые российские и европейские вузы решают проблему повышения качества математической подготовки поступивших к ним студентов, организуя для них в первом семестре дополнительные выравнивающие ( корректирующие , адаптационные ) курсы [Гридчина, Осипова, 2018; Кочеткова, Кытманов, 2016; Мамае-

ва, 2011; Степкина, Байгушева, 2016; Bardelle, Di Martino, 2012]. Как правило, таким курсам предшествует входное тестирование.

Во многих американских вузах выравнивающий курс математики рекомендуется в первом семестре студентам, показавшим низкие результаты при входном тестировании [Reddy, Harper, 2013;

¹ Исследование выполнено при поддержке РФФИ, проект № 18-013-00654.

Rueda, Sokolowski, 2004]. В зависимости от политики, проводимой университетом, такой курс может являться обязательным, и только после его завершения студент может приступить к изучению дисциплин высшей математики [Hsu, Bressoud, 2015].

В некоторых случаях корректировка уровня подготовленности первокурсников к обучению в вузе осуществляется с использованием электронных образовательных ресурсов [Макаров и др., 2017; Bardelle, Di Martino, 2012; Goonatilake, Chappa, 2010; Reddy, Harper, 2013].

В Сибирском федеральном университете (СФУ, Красноярск) начиная с 2013/14 учебного года все студенты первого курса инженерных направлений подготовки в начале сентября проходят входное тестирование по разделам школьной математики. После этого для указанных студентов организуется так называемый дополнительный адаптационный курс , призванный восполнить пробелы в знаниях элементарной математики и обеспечить необходимую базу математической подготовки будущего инженера [Кочеткова, Кытманов, 2016].

Цель исследования – анализ результатов входного тестирования по математике первокурсников СФУ за период с 2015 по 2018 г., описание структуры и компонентов адаптивного электронного обучающего ресурса (АЭОР) , созданного для web-поддержки изучения модуля математической дисциплины, а также оценка эффективности использования АЭОР студентами с разным уровнем школьной подготовки. Эмпирической базой исследования послужили результаты студентов направления подготовки 09.03.01 Информатика и вычислительная техника, которые обучаются в институте космических и информационных технологий СФУ.

Входное тестирование проводится в компьютерном классе в формате интернет-тестирования. Используются тесты, разработанные Научноисследовательским институтом мониторинга качества образования (НИИ МКО, Йошкар-Ола). Каждый тест включает в себя 21 задачу по школьному курсу математики. Более точно представлены задания по следующим темам.

• 1.    Степени и корни.

• 2.    Тождественные преобразования алгебраических выражений.

• 3.    Преобразования тригонометрических выражений.

• 4.    Тождественные преобразования логарифмических выражений.

• 5.    Задачи из практической деятельности и повседневной жизни.

• 6.    Текстовая задача.

• 7.    Уравнения с переменной под знаком модуля.

• 8.    Иррациональные уравнения.

• 9.    Логарифмические уравнения.

• 10.    Тригонометрические уравнения.

• 11.    Системы линейных уравнений.

• 12.    Квадратные неравенства.

• 13.    Показательные неравенства.

• 14.    Область определения функции.

• 15.    Графики элементарных функций.

• 16.    Производная функции.

• 17.    Наименьшее и наибольшее значения функции.

• 18.    Геометрический смысл определенного интеграла.

• 19.    Элементы комбинаторики, статистики и теории вероятностей.

• 20.    Решение прямоугольных треугольников.

• 21.    Применение геометрических знаний для решения практических задач.

В 2015 и 2016 гг. во входном тестировании приняли участие соответственно 113 и 102 человека, а в 2017 и 2018 гг. количество студентов, прошедших входной тест, составило 79 и 100 человек соответственно. Результаты входного тестирования представлены на рис. 1–4.

В таблице приведены средневзвешенные проценты правильно выполненных заданий за четыре года. Как мы видим, студенты лучше всего справились с задачами 5–6, 11 и 19. Напротив, наибольшие трудности вызвало решение задач 2-3, 8-10, 14, 16-18 и 21; при этом, за исключением задач 2 и 14, низкие результаты стабильны и повторяются на протяжении всех четырех лет. Отметим также, что абсолютное большинство ошибок студенты совершили при выполнении заданий 3 и 10, связанных с тригонометрией.

Средневзвешенные результаты входного тестирования в период с 2015 по 2018 г.

Weighted average results of preliminary testing from 2015 to 2018

№ задачи	1	2	3	4	5	6	7	8	9	10	11
Количество студентов, правильно выполнивших задание, %	68	52	42	66	90	80	71	49	45	44	86
№ задачи	12	13	14	15	16	17	18	19	20	21
Количество студентов, правильно выполнивших задание, %	64	60	55	77	48	49	48	85	76	52

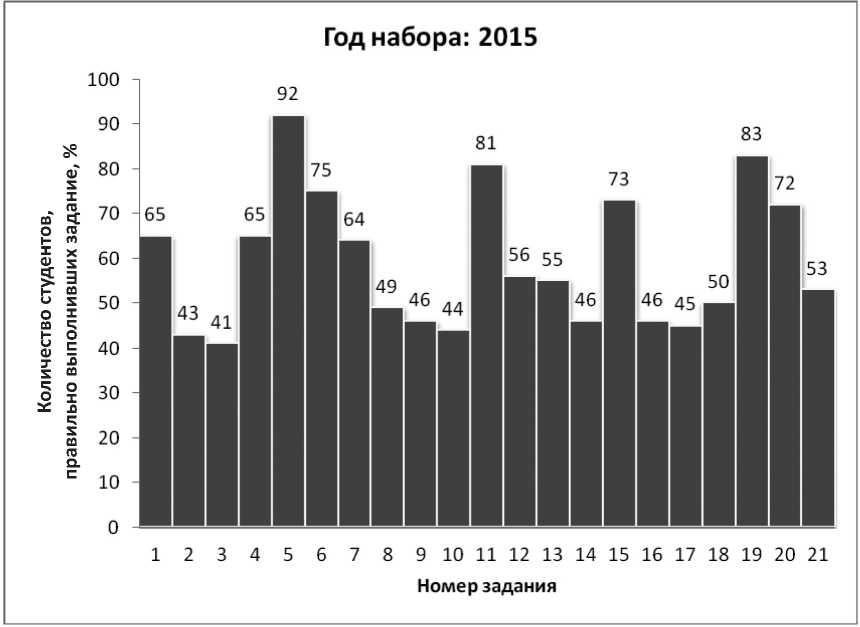
Рис. 1. Результаты входного тестирования студентов, 2015 г.

Fig. 1. Student placement testing results of 2015

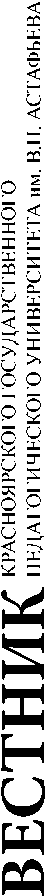
Рис. 2. Результаты входного тестирования студентов, 2016 г.

Fig. 2. Student placement testing results of 2016

Год набора: 2017

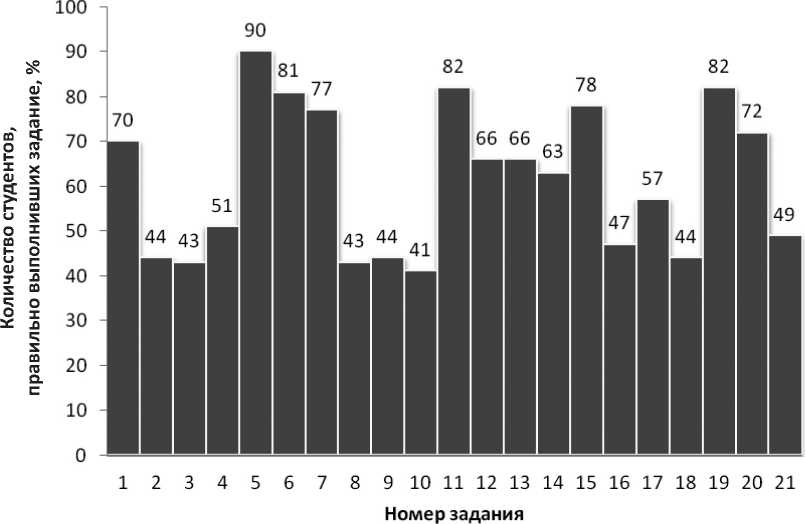
Рис. 3. Результаты входного тестирования студентов, 2017 г.

Fig. 3. Student placement testing results of 2017

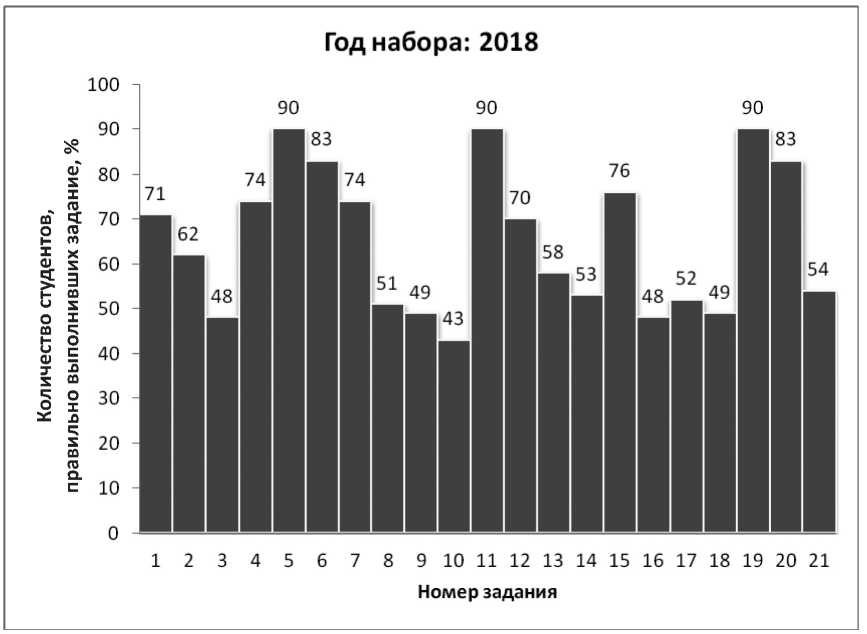
Рис. 4. Результаты входного тестирования студентов, 2018 г.

Fig. 4. Student placement testing results of 2018

Обращает на себя внимание тот факт, что больше половины первокурсников допустили ошибки в задачах 16–18, относящихся к высшей математике. В связи с этим возникает вопрос, насколько целесообразно включать в курс школьной математики элементы дифференциального и интегрального исчислений? Среди российских и зарубежных ученых нет однозначного мнения на этот счет [Гладкий, 2009; Sadler, Sonnert, 2018].

Анализ результатов входного тестирования первокурсников выявил ряд тем школьного курса математики, уровень остаточных знаний по которым ниже среднего. При этом указанная тенденция сохраняется на протяжении нескольких лет. Речь идет о таких темах, как преобразование тригонометрических выражений, решение иррациональных, логарифмических и тригонометрических уравнений, применение геометрических знаний для решения практических задач, а также производная и определенный интеграл.

Результат входного тестирования первокурсников является веским основанием для организации дополнительного адаптационного курса по математике в СФУ для студентов инженерных направлений подготовки. Продолжительность курса составляет 3 месяца, и по его завершении студенты проходят повторное тестирование.

В 2018 г. в повторном тестировании приняли участие 88 студентов направления подготовки Информатика и вычислительная техника. Результаты тестирования приведены на рис. 5. На диаграмме темным цветом изображены результаты входного тестирования, а более светлым - прирост результатов при повторном тестировании. Как мы видим, самый значительный рост (36 %) достигнут при решении задачи 16 (вычисление производной функции), что вполне закономерно, поскольку студенты изучали эту тему также и в курсе математического анализа.

Вместе с тем для задач 19 и 20 результаты остались на том же уровне, что и при входном тестировании, а для задач 6 и 21 они улучшились не более чем на 5 %. Это может быть обусловлено, в частности, низкой мотивацией первокурсников при повторении указанных тем, поскольку они слабо связаны с разделами математики, которые изучаются в первом семестре (алгебра и аналитическая геометрия, математический анализ).

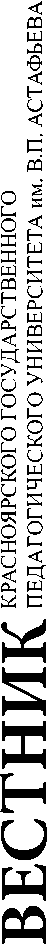
Год набора: 2018 (повторное тестирование)

ф'

га со

ф со

О

ф

о в га а в

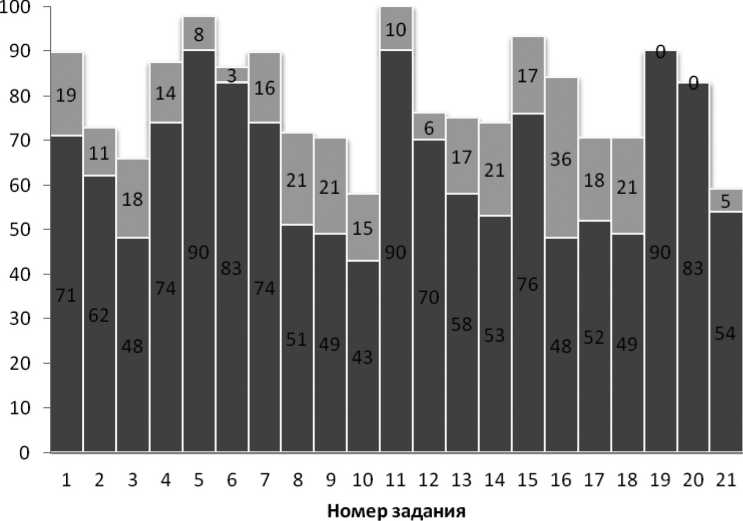
Рис. 5. Результаты повторного тестирования студентов, 2018 г.

Fig. 5. Student retesting results of 2018

Отметим, что существует ряд факторов, которые снижают эффективность адаптационного курса. В частности, такой курс, как правило, слабо персонализирован, то есть если и учитывает индивидуальные потребности обучающихся, то в очень малой степени. Кроме того, многие студенты не имеют достаточной мотивации для посещения таких занятий, поскольку не вполне осознают, каким образом повторение школьной математики поможет им в освоении программы первого курса университета, или же считают уровень своей подготовки достаточным для успешного обучения в вузе.

Очевидно, уровень школьной математической подготовки влияет на результаты обучения первокурсников [Agustin, Agustin, 2009; Madison et al., 2015; Reddy, Harper, 2013]. Студенты могут уверенно оперировать новыми понятиями и применять методы дифференциального и интегрального исчислений, но при этом часто допускают ошибки в действиях, относящихся к элементарной математике. Как показывает опыт авторов настоящей статьи, особенно часто сегодняшние студенты ошибаются, выполняя упро щение выражений, сокращение дробей, извлечение корня из суммы или разности величин, а также при проведении тригонометрических вычислений.

Вместе с тем в последние годы появились эмпирические исследования, которые не подтверждают, что результаты входного тестирования, а также прохождение выравнивающего курса школьной математики позволяют предсказать, будет ли обучающийся успешен при освоении математических дисциплин на первом курсе [Hsu, Bressoud, 2015; Medhanie et al., 2012].

Исследуем вопрос, насколько результаты повторного тестирования по школьной математике первокурсников 2018 г. набора коррелируют с их результатами освоения модуля «Интегралы функций нескольких переменных (Интегралы ФНП)» дисциплины «Математический анализ». Модуль изучается во втором семестре первого курса и включает в себя двойные, тройные, криволинейные и поверхностные интегралы, а также элементы теории поля.

Для web-поддержки изучения указанного модуля нами разработан адаптивный электрон- ный обучающий ресурс, функционирующий на базе системы управления обучением Moodle и размещенный на платформе электронного обучения СФУ.

АЭОР спроектирован в соответствии с концепцией адаптивного обучения в электронной среде [Шершнева, Вайнштейн, Кочеткова, 2018; Brusilovsky, 1999]. Обучающий ресурс рассматривается нами в качестве организационнопедагогического средства, способствующего приобретению обучающимися знаний и опыта, выработке умений, что в результате приводит к формированию компонент их профессиональной компетентности [Shershneva et al., 2016].

При разработке образовательного контента АЭОР применяется стратегия микрообучения, которая состоит в том, что весь учебный материал структурируется небольшими порциями [Шершнева, Вайнштейн, Кочеткова, 2018; Buchem, Hamelmann, 2010; Lindner, 2006; Schmidt, 2007]. Минимальную порцию учебного материала мы называем юнитом . Адаптация учебного контента осуществляется за счет нескольких редакций изложения материала каждого юнита, которые отличаются степенью детализации и формой представления: текст с рисунками, видеоматериалы, интерактивные ресурсы.

Для оценивания результатов обучения разработаны 11 тестов к юнитам, три теста-тренажера, а также задачи для самостоятельного решения с ответами. Тесты к юнитам предназначены для проверки знания и понимания текущего материала, умения применять свойства интегралов ФНП, а также анализировать взаимосвязи между ними. Что касается тестов-тренажеров, то они помогают обучающемуся выработать умения, связанные с вычислением различных типов интегралов ФНП.

Для прохождения тестов к юнитам предусмотрены две попытки без ограничения времени, но с установленными проходными баллами. По окончании первой попытки студент получает немедленный отзыв на свое решение и доступ к материалу, изложенному в другой редакции. Изучив его, обучающийся может пройти повторное тестирование. Если в обеих попытках ему не уда- ется набрать проходной балл, то он обращается за консультацией к преподавателю, после которой получает дополнительную попытку для выполнения теста. В тестах-тренажерах количество попыток не ограничено, а проходные баллы не установлены. Во всех тестах в зачет идет лучшая попытка.

Навигация по элементам АЭОР автоматизирована. Обучающийся получает доступ к следующему элементу только после успешного завершения предыдущего. При этом изучение материала следующего юнита начинается с редакции того типа, который обеспечил студенту лучший результат при освоении предыдущего.

Из 88 первокурсников, прошедших повторное тестирование по курсу школьной математики, 44 человека изучали модуль «Интегралы ФНП» с помощью АЭОР (далее – адаптивный модуль ). Отметим тот факт, что все студенты, изучавшие адаптивный модуль, смогли получить положительную оценку (отлично, хорошо или удовлетворительно), в то время как этого сделать не удалось трети студентов, изучавших модуль без использования АЭОР и имеющих при этом высокие баллы тестирования по школьной математике.

Рассмотрим две случайные величины: Х = {баллы, набранные студентом при повторном тестировании по школьной математике} и Y = {баллы, набранные студентом при освоении адаптивного модуля}. Все результаты фиксируются по 100-балльной шкале. Выборочный коэффициент корреляции величин Х и Y равен r в = 0,22. Для оценки его значимости используем критерий Стьюдента. В качестве основной рассматриваем гипотезу H ₀: r в = 0 при альтернативной гипотезе H 1 : r _в * 0, уровень значимости а = 0,05. Вычисляем наблюдаемое и критическое значения статистики. Поскольку гипотеза H ₀ принимается, то с вероятностью 0,95 величины Х и Y некоррелированы.

Итак, не установлено значимой корреляции между уровнем школьной подготовки первокурсников по математике и результатами изучения модуля математического анализа. Другими словами, высокие баллы входного тестирова-

ния не являются гарантией такого же успешного освоения студентом дисциплин университетской математики. Вместе с тем студенты, имеющие значительные пробелы в школьной подготовке, смогли успешно справиться с изучением адаптивного модуля. Использование АЭОР при освоении дисциплины позволило каждому студенту построить индивидуальную образовательную траекторию, тем самым повысив результативность обучения.

Таким образом, мы убедились, что изучение модуля математической дисциплины с применением адаптивного электронного обучающего ресурса позволяет достичь положительного результата всем студентам, независимо от уровня их школьной математической подготовки.