Агент-ориентированная модель инновационного процесса появления, отбора и реализации инновационных идей

На современном этапе в Российской Федерации наметилась тенденция перехода от бюджетного обеспечения компаний по производству благ, близких к общественным (например, газовое и энергообеспечение, услуги ЖКХ), к автономным образованиям с бюджетными дотациями. В результате обострилась проблема эффективного регулирования рыночного сектора экономики с высокой степенью монополизации. Именно к нему относятся указанные компании. Данная проблема важна на уровне как Федерации, так и любого административно-территориального образования.

Наиболее эффективным способом регулирования таких рынков является тарифное регулирование. На данный момент тарифы формируются исключительно затратным методом, что не позволяет монополиям получать сверхприбыли, но при этом никак не регулируется конкурентная составляющая рынка [12]. Суть тарифного регулирования монопольных рынков предполагает включение в тариф составляющей, которая отражает реакцию государства на естественную монополию. Это позволит ограничить монопольную власть и не затронуть само существование таких монопо- лий, так как они производят блага высокой общественной полезности. Таким образом, влияние на монополизированный рынок, а также адаптация к изменению ситуаций на нем является важной характеристикой эффективности деятельности государства.

Основная сложность при разработке способов регулирования монополизированных рынков, особенно рынков естественных монополий, обусловлена нестабильностью, связанной с противоборством интересов государства, как защитника свободного конкурентного рынка, и естественного монополиста как гаранта снабжения населения жизнеобеспечивающими благами. Эта ситуация требует динамического государственного вмешательства с целью обеспечения баланса интересов монополии и общества.

Эффективность системы управления, мобильность реакции на внешние изменения зависит от адаптивности. Под адаптивностью понимается основное свойство, обеспечивающее устойчивость деятельности и способность системы управления не только реагировать на внешние изменения, но также прогнозировать их.

Наиболее глубокое исследование в области адаптивности именно государства принадлежит В.А. Мау, который в цикле статей «Логика российской модернизации» [6] указывает на то, что проблемы оценки и повышения адаптивности целесообразно решать не только в сфере стратегического управления предприятиями, но и в сфере государственного управления.

Общий подход к решению задачи

Решение проблемы происходит пошагово. После установления государством определенных условий ситуация на рынке становится на определенное время стационарной. Рынок на каждом шаге рассматривается как замкнутая система, государство (внешние условия) на него не влияет, после выбора способа влияния на конкретном шаге и изменения условий на рынке начинается новый шаг. Для того чтобы выбрать оптимальную стратегию, государство рассматривает замкнутый рынок, в результате чего у него есть возможность получить крайние варианты интересующих характеристик рынка и затем из вариантов определяется один, подходящий для государства, и исходя из него избирается новая стратегия государства. Скорость, эффективность, оптимальность выбора корректирующего варианта государственной политики, момента его выбора характеризует адаптивность государства.

Исходя из этого на каждом шаге решается 2 вопроса:

• 1.    Построение модели взаимодействия монополиста и покупателя при заданных корректирующих государственных регуляторах (налоги, акцизы, дотации, гранты и т.п.), представленных матрицей A.

• 2.    Построение модели взаимодействия государства с рынком и оценка характеристик адаптивности государства.

Поскольку изменение внешних условий работы объекта управления далеко не всегда поддается прогнозированию, то для анализа процессов адаптации используют аппарат теории принятия решений в условиях риска и неопределенности. Процесс функционирования в нестабильной среде представляют в виде динамической стохастической игры государства и рынка . В данном случае рынок – игрок, хотя и действующий сознательно, но имеющий не связанную с игрой цель. Состояния рынка, в свою очередь, можно рассматривать как результат игры продавцов с покупателями с учетом правил функционирования рынка. Первым этапом исследования является решение задачи поиска этих состояний.

Построение модели рыночного окружения государства

Несмотря на специфику монополизированного рынка, взаимодействие каждого конкретного покупателя с монополистом и всех покупателей с монополистом следует рассматривать как конфликты. Для определения ситуации на рынке, т. е. для разрешения конфликта, применяется аппарат теории игр.

Однако монополизированный рынок имеет характеристики, которые вносят особенности в формализацию игры и, следовательно, ее решение. Для того чтобы определиться со способом решения, необходимо определить вид решаемой игры. Анализ экономической сущности монопольного рынка показывает невозможность отнесения рассматриваемого вида конкуренции к одному из следующих классов игр [9]:

• 1.    Антагонистические игры – предполагают абсолютную противоположность интересов участников, тогда как при монопольной конкуренции у монополиста и покупателей различные, но не противоположные цели.

• 2.    Коалиционные (кооперативных) игры - рассматривают вопросы взаимодействия групповых игроков. При монополии потребители могут рассматриваться как коалиция, но действующая без координации действий своих участников. Монополист представляет собой одного единственного субъекта М.

• 3.    Рассмотрение взаимодействия монополиста и множества отдельных потребителей, как это реализуется в бескоалиционных играх, может привести к существенному усложнению расчетов, если множество потребителей достаточно велико. Поскольку на рынке естественной монополии все потребители характеризуются сходными свойствами (невозможность единолично влиять на рынок, невозможность в чистом виде создавать значимые коалиции и т.д.) и одинаковой целью (максимизация потребительской полезности), то будем рассматривать всю совокупность потребителей как единого игрока П.

Исходя из проведенного анализа монополизированные рынки будем рассматривать в виде бескоалиционной игры двух лиц: монополиста M и обобщенного потребителя П.

Игровой процесс заключается в следующем [11]. Игрок M предлагает потребителям товар, пытаясь максимизировать прибыль (рис. 1) за счет увеличения ценовых характеристик товара. Игрок П, сравнивая неценовые характеристики и потребительскую выгоду от них с запрошенной ценой, формирует величину потребности в каждом из товаров. Уменьшение потребности игрока П в товаре влияет на величину получаемой прибыли от реализации этого товара игроком М.

ВЕСТНИК ПЕРМСКОГО УНИВЕРСИТЕТА

ЭКОНОМИКА             Спец. выпуск

Игрок М: монополист

цель: максимизация

Ценовые

Неценовые

характеристики

характеристики

цель: максимизация

Игрок П: потребители

Рис. 1. Связь интересов игроков и характеристик товара

С позиции теоретико-игрового подхода игровой процесс на рынке в общей форме можно            выразить            кортежем

Г= М,П , XM,Xn , HM,Hn  , где    М    –    предприятие-монополист,

I = i =1,2,..., П - множество стратегий монополиста; S i – предложение монополиста покупателям с использованием технологии i = 1, П (определяется товар и его цена Pi );

П – множество предприятий-потребителей, J = j = 1,2,..., m - множество стратегий потребителей; D – рыночный спрос потребителя на товары с потребительскими свойствами j = 1, m (определяются группы потребителей и объемы их потребления V j );

H     P^TV        – матрица выигрышей     игры     монополиста,     где

P ( i ) V ( j )-A м ( i , j ) — прибыль монополиста при наступлении ситуации i , j , P ( i ) -цена, установленная монополистом, V ^{( j} ) - ^объ ем, который согласны купить потребители при объявленной цене;

H      PTV        – матрица выигрышей игры Г покупателей, где - P (i )V (j ) + An( i, j ) – совокупная полезность ситуации i, J для потребителей.

Формализовано цель монополиста можно выразить: P^TV — А_м —> max , а цель потребителя: —P^TV + Д _п —> max . При этом и – матрицы государственного воздействия соответственно на монополиста и потребителя. Воздействие на игроков со стороны государства не обязательно одинаковое ( А_м ( i , j ) ^ А_п ( i , j ) ), но рассматривается замкнутая система и предполагается, что все средства, полученные от монополиста, перераспределяются между потребителями

X ^ЛМ ⁽ i , ^j > Z ^ЛП⁽ i , ^j ) .

iel , jeJ iel , jeJ

На данном этапе исследования важно сделать следующее допущение: государство действует на основе только неценовых рычагов, например налоговое регулирование, тарифное регулирование и т.д., но не непосредственным установлением цены. Государство может воздействовать на платежные матрицы, корректировать их на выбранные и , но не может полностью устранить конфликт между покупателем и монополистом путем задания цены на рынке. Рынок принимает вид двух платежных матриц (рис.2).

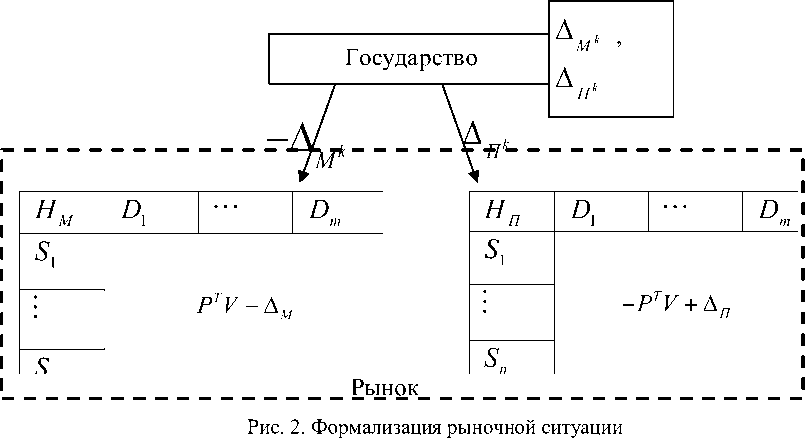
В реальных рыночных ситуациях, как правило, число участников рынка достаточно большое, при этом существует огромное количество возможных стратегий каждого игрока. Так как игрок П имеет составную структуру, а потребность в каждом товаре формируется независимо каждым из потребителей, то разумным является рассмотрение смешанного расширения сформулированной выше биматричной игры в терминах интенсивностей использования игроками своих чистых стратегий.

Применение модели адаптации государства к изменениям природы не имеет строгих ограничений, однако демонстрация использования модели была начата с идеализированной ситуации, чтобы количество возможных явлений природы было наименьшим: рассматривался частный пример рынка с высокой монопольной властью – монопольно-монопсонический рынок [5], а затем сделано обобщение на классический монопольный рынок.

Приведем конкретный пример монополь-но-монопсонического рынка – рынок нефтяного попутного газа (НПГ) в Западно-Сибирском регионе [12]. Несмотря на то, что переработка НПГ технологически жестко связана с его добычей, две фазы единого технологического процесса выполняют различные независимые фирмы на основе рыночных отношений. Цель государства – с помощью неценовых рычагов управления не дать надолго установиться цене на НПГ, так как это влечет за собой доминирование одной из сторон и разорение другой. Государство должно постоянно адаптироваться к изменяющимся ценам. Анализ рынка позволяет формализовать задачу в виде игры, результаты которой зависят в конкретном примере от величины штрафа (политики государства) и издержек на транспортировку, которые составляют основную часть затрат компаний. По результатам решения игры получены формулы для расчета цен на НПГ, отражающие состояния на рынке – состояния природного окружения государства.

Следующим этапом стало обобщение модели адаптивности государства на классический монопольный рынок. В качестве примера рынка односторонней монополии рассматривается рынок, образованный продавцом услуг по обеспечению газопроводов, в частности, Златоустовским филиалом ООО «Челябинскрегионгаз». Данное предприятие хоть и не является чистым монополистом, но его единственный конкурент на рынке данных услуг занимает лишь около 13–15 % рыночного сбыта, сам рынок обладает всеми признаками монополистического.

Нахождение вариантов рыночного окружения государства

Для антагонистических игр принципы минимакса, максимина и равновесия совпадают (если они реализуемы). В таком случае они определяют единое понятие оптимальности и решения игры. В теории неантагонистических игр нет единого подхода к выработке принципов оптимальности. Имеется множество принципов оптимальности, каждый из которых основывается на некоторых дополнительных предположениях о поведении игроков и структуре игры.

При моделировании монополизированного рынка эффективно использовать равновесие по Штакельбергу. Монополист – лидер, может объявлять цены, покупатель – ведомый. В чистых стратегиях поиск равновесия, по Штакельбергу является простой задачей за исключением случаев, когда существует несколько вариантов с равными выигрышами для ведомого и разными для лидера. В таком случае прогнозирование поведения ведомого практически невозможно. Однако в рассматриваемом примере – исключить заведомо неэффективные для общества стратегии и варианты игры – является задачей государства и ограничение таких случаев входит в матрицу A.

В чистых стратегиях ситуация i, j 11 J J, называется М-равновесием по

Штакельбергу в игре двух лиц Г, а H , называется M-выигрышем, если j i Z i , Z^ i = arg max Hn i, j   и выполня- jJ ется равенство  HM =max Hn i, j (i) .

i

Понятие равновесия можно интерпретировать следующим образом. Игрок М (лидер) знает функции выигрыша обоих игроков, а следовательно, и множество наилучших ответов игрока П (ведомого) на любую стратегию игрока M. Тогда он, обладая этой информацией, максимизирует свой выигрыш,         выбирает         стратегию

i*= arg max HM i, j(i) . Таким образом, iI

H – выигрыш М игрока, действующего опти-м мально в качестве лидера в игре Г.

Необходимо отметить, что равновесие по Штакельбергу в чистых стратегиях не отражает некоторых особенностей моделирования реальной монопольной рыночной ситуации, а именно не отражает доли мнения каждого отдельного покупателя в формировании совокупного спроса на товар и доли каждой технологии в общем технологическом процессе монополиста (монополист имеет возможность использовать в производстве не одну стратегию, а несколько одновременно в разных долях). Следовательно, наиболее близкой к реальным условиям является нахождении равновесия по Штакельбергу в смешанных стратегиях [8].

В смешанных стратегиях выигрыш монополиста         задается         выражением qT PTV       s , выигрыш потребителей qTPTV       s , где q – распределение общего объема производства (реализации) товара монополистом по различным технологиям, а s – распределение общего объема потребления товара потребителями по различным группам, обладающим различным спросом.

„              *   *

Ситуация q , S называется ситуаци- ей равновесия по Штакельбергу, если:

s* = arg max |^q*T ppVp + An s^,

s q = argmax qqT -PTF + An s],

q = arg max qq P V — AM s q J.

В результате игры монополиста и покупателей получаем ситуацию равновесия на рынке ( q ^k , s^k ) при заданной политике государства

(т.е. матрицах k , k ). По прошествии неко- торого времени из-за нестационарности матрицы

P V текущее равновесие на рынке может перестать удовлетворять потребности государства. Цель установить на рынке новое, «справедливое», положение равновесия (q , s ) государство дос- тигает за счет изменения матриц k и k на

А к +1    ж к +1

и         .

к+1

Решение задачи построения матриц

к+1

и      нетривиально. Для построения таких мат- риц в некоторых условных дискретных шкалах величин q и s предлагается построить матрицы к+1               к+1

Ам i, j и Ап i, j для всех возможных равновесия     (q , s

вариантов равновесия в чистых стратегиях, а затем найти требуемую для установления положения

*

А к ;¹ = £ A * ;¹ i , j q * s * .

i^I , JJ

Корректирующие            матрицы а к+1 •* •*           а к+1 •* •*

AM i , j и An i , j можно найти

*4*

для каждой пары i , j как решение задачи смесь    матриц

линейного программирования

У un (i, J) + uM (i, J) ->max

IJJ                          ^u ’^A

• -u, (i, J )^An(i, J) ^un (i, J), w. T . T\        -uM(i,JM<(i,J)^uM(i,J)>

v I E 1 , J EJ \

• -p(i)V(J) + An(i,J)<-p(i)V(J ) + Дп(i,J ), p (i )V (J )-Дм( i, J )< p (i V (J )-Дм( i ’, J)

(i,J)=      ^n(i,JX  uM,un -°.

iel , JeJ                  iel , JeJ

Нужно отметить, что, несмотря на опти- А к +1     А к +1

мальность матриц      и      , переход к ним не всегда при конкретных внешних условиях эффективен. Например, в случае если переход к новой стратегии требует слишком высоких финансовых затрат или длительной временной задержки, которая повлечет критическую ситуацию на рынке. Такие ситуации не исключаются, так как кроме

А к +1      А к +1

замкнутости системы на       и       другие ограничения в условиях рассматриваемой задачи не накладываются.

Построение модели адаптивности го- сударства к рыночному окружению

Второй функциональный блок исследования посвящен построению игровой модели адаптации государства к изменениям на рынке. Модель представлена в форме стохастической игры. В качестве состояния рынка выступают сочетания параметров P и V, а стратегий активного игрока – принимаемые государством политиче- ские решения, на основе которых строятся матри-

A k +1 цы ^м и

д ^{k +1} ^п

Далее будем использовать аналитические методы количественной оценки адаптивности, предложенные в статье «Методы анализа адап- тивности производственных программ и организационных структур предприятий» [2]. При построении модели взаимодействия государства с рынком и оценке адаптивности государства используется следующая система показателей:

– цена полной информации ( Аv ), ожидаемый выигрыш при идеальной (мгновенной, без затрат), но недостижимой адаптации государства к новым условиям ;

– интегральная стоимостная оценка степени адаптивности государства ( C     ), ожи даемый поток затрат и потерь государства, связанных с адаптацией к меняющимся условиям;

– относительная мера адаптивности ( 0 ), доля потенциально возможного выигрыша от адаптации, которая теряется из-за ненулевых затрат времени и средств на осуществление перехода;

– относительная мера чувствительности государства к изменению условий рынка ( Y ).

На основе системы показателей производится анализ степени адаптивности управляющей системы и целесообразность адаптации к изменениям с учетом необходимости проведения дополнительных затрат.

Расчет показателей адаптивности государства

Адаптивность государства определяют конечные затраты времени и средств, связанные с переключением на новую политику. Обозначим с+ непосредственные затраты на переход государства от политики лклк + 1, tk,k1 – среднюю продолжительность перехода. Матрицы затрат средств и времени на смену стратегии C и T квадратные, размерностью ll, имеют нулевую главную диагональ, поскольку при отсутствии смены стратегии затраты средств и времени на переключение отсутствуют.

Примем предположение, что переключение всегда происходит оптимальным образом, т.е. государство рассматривает переход именно на стратегию Л к ₊ , которая будет оптимальной в новых условиях. V – матрица условных выигрышей государства от выбора стратегии k +1 при состоянии рынка l .

В решаемой в работе задаче у природы небольшое количество состояний, что сужает область возможных ее изменений во времени. Поэтому в качестве показателя изменения удобнее использовать не новое состояние, в котором окажется рынок, а сам факт перехода к другому состоянию, а именно вероятность такого перехода. Рынок может переходить из состояния l в l с некоторой интенсивностью л . Интенсивность – это вероятность того, что рынок, будучи изначально в состоянии l , перейдет в l в течение единицы времени. Случайный процесс смены состояний рынка описывается переходной матрицей

A , состоящей из элементов

. Их оценка

осуществляется экспертным путем.

По прошествии достаточно длительного времени, превышающего по порядку величину 1

, произойдет статистическая стабилиза- min л l,lll ция состояний рынка и каждому состоянию будет соответствовать некоторая финальная вероятность p . Ее физический смысл – средняя доля времени пребывания рынка в состоянии l . Финальные вероятности можно вычислить как компоненты собственного вектора транспонированной переходной матрицы, которому соответствует собственное число, равное 1. Так вектор (столбец) финальных вероятностей удовлетворяет условию AT p   p . При этом частота переходов рынка из одного состояния в другое, т.е. среднее число переходов в единицу времени, равна hllplл II f . Элементы h ' II составляют матрицу частот переходов H .

Если известны вероятности состояний рынка, задача выбора предприятием оптимальной стратегии становится задачей принятия решений в условиях риска. Если избрать какую-либо стратегию k в качестве стационарной, т.е. постоянно придерживаться ее при всех изменениях состояний рынка, ожидаемый выигрыш составит

n vk =2vlkpl.

l 1

Оптимальной стационарной стратегией stat k    в данной игре является такая стратегия, которая обеспечивает максимальный ожидае-

stat мый выигрыш k

Если бы в предприятие могло

argmax v .

k каждом состоянии рынка придерживаться стратегии,

оптимальной именно для данного состояния, т.е. kpt = arg max v_lk\l , то ожидаемый выигрыш повысился бы до уровня

%% предприятие вынуждено придерживаться стратегии , которая уже не является оптимальной в новых условиях. Z – матрица полных стоимостей переходов. Ожидаемый поток затрат и потерь государства, непосредственно связанных с его адаптацией к меняющимся условиям, равен

V max

l

, opt

p_l       max v_lk l p_l .

l 1 ^k

В теории статистических игр разность

v  vmax  max vk      max vlk k             l1k

l pl max    vlk pl k       l1

называется ценой полной информации. v

–

это ожидаемый выигрыш при идеальной, но недостижимой в реальности адаптации государства к новым условиям, т.е. происходящей мгновенно и без затрат.

На основании матриц C , T и платежной матрицы V можно составить матрицы затрат средств и времени на смену стратегии предприятия при каждом переходе рынка из одного состояния в другое, имеющие размерность ll . Элементы матрицы затрат средств C равны непосредственным затратам на смену стратегии, оптимальной в состоянии рынка l , на стратегию, оптимальную в состоянии l :

^Садапт   е е   ^hll zll у^.

l = 1 l ^ 1

Величину С     можно считать инте гральной стоимостной оценкой степени адаптивности государства. Данная оценка является скалярной, а не векторной величиной, что упрощает моделирование поведения игрока и процесс принятия решений. Однако само по себе абсолютное значение С      недостаточно информативно. Наиболее наглядной экономической оценкой степени адаптивности предприятия, в рамках предлагаемой модели, следует считать отношение показателя интегральной стоимостной оценки к цене полной информации

b _ ^Садапт

.

ў

opt , opt

Аналогично, матрица затрат времени

T составлена из элементов II % ,11 :

D v

Эта величина является относительной мерой адаптивности и показывает, какая доля потенциально возможного выигрыша от адаптации государства к меняющимся условиям теряется за счет ненулевых затрат времени и средств, связанных с изменением стратегии. Если Ь < 1 , то гибкое переключение стратегий является целесообразным и стратегия неэффективна.

Отношение цены полной информации к ожидаемому выигрышу при оптимальной ста-

ционарной стратегии _ D v

max v kk

.

ll ў ll ^ў . k opt , k opt

Время, необходимое для переключения на новую стратегию, по порядку величины должно быть много меньше характерного времени непрерывного пребывания рынка в том или ином состоянии – иначе переключение заведомо бессмысленно. Кроме того, выполнение данного ограничения позволяет свести два параметра – время и стоимость переключения – только к стоимости следующим образом:

zu у   % + %% ( ^{( v}iyo^

—

^Vl ,k k ept ),

^{где f}lfy^(vl ><

—

^vl ў, k o^lpt

) - упущенная

Данная величина может служить относительной мерой чувствительности государства на изменения условий на рынке и наряду с b определяет целесообразность адаптации к этим изменениям g > 1 говорит о целесообразности гибкого изменения стратегий государства.

Разработка программы для расчета показателей адаптивности:

Итогом исследования стала структура программы для расчета рассмотренных показателей адаптивности государства. Программа разработана на языке C#, реализованном на платформе Visual Studio 2005. Схема расчета оценки адаптивности отражена на рис. 3 .

выгода вследствие того, что в течение времени

вход ввод данных об объемах поставок N потребителям решение игры взаимодействия монополиста с покупателями результат: возможные состояния рынка ввод платежной матрицы V – условные выигрыши госу-дарства от выбора стратегии k при состоянии рынка l преобразование матрицы V : исключение стратегий, которые при любом l не л чше хотя бы 1 из оставшихся k ввод матрицы интенсивности изменений на рынке A расчет вектора финальных вероятностей p методом Жордана – Гаусса из СЛАУ Aґp =O расчет матрицы частот переходов H =A.ґp расчет ожидаемого выигрыша v =е V .ґp

MS Excel

выигрыш при идеальной адаптивности v

=max V ґp

k

l

D v = v max

-

max v kk

Цена полной информации

Интерфейс

ввод матриц материальных ( C ) и временных ( T ) затрат расчет непосредственных затрат на смену стратегий C\ T (используем V , C , T ): % = ckl к1 ? , %1у = til   ?

kopt ,kopt               kopt ,kopt расчет матрицы полных стоимостей переходов Z

——Z^ck+tv^v^^

C_адапт = ее h_{ll ў}Ч z_l

l

l ў

ll ў

Ожидаемый поток затрат и потерь от адаптации

адапт

D v

D v g =---— max v kk

Доля потенциального выигрыша от адаптации, теряющаяся из-за ненуле вых затрат

Относительная мера чувствительности к изменениям на рынке выход

Рис. 3. Схема программы для расчета показателей адаптивности государства

Из схемы программы видно, что в качестве исходных данных программы поступают 4 потока. Потоки являются автономными. Из всех исходных данных информация об объеме поставок товара монополистом потребителям (для расчета возможных состояний рыночного окружения государства) является статистической информацией.

Ведение бухгалтерской и налоговой отчетности во многих российских компаниях осуществляется посредствам ППП 1С: Бухгалтерия. Реализована косвенная опосредованная связь программы с 1С. Пакеты фирмы 1С имеет функцию экспорта данных в MS Word и MS Excel. В то же время ориентированность языка С# на пакеты Microsoft дает возможность достаточно свободно взаимодействовать с MS Excel. Это позволило реализовать следующую схему (рис. 4).

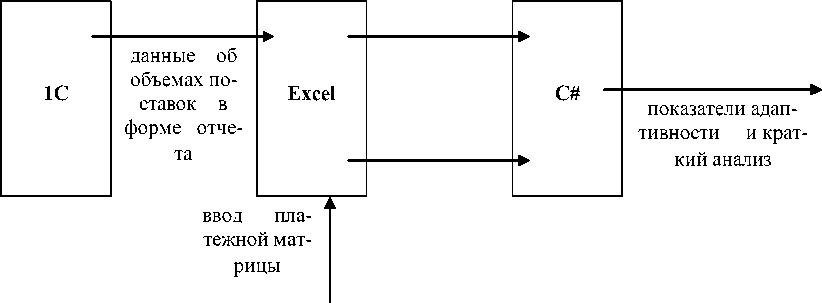
Рис.4. Схема экспорта – импорта данных

Платежная матрица, матрица интенсивности изменений на рынке и матрицы затрат на адаптацию являются «труднооцениваемыми» показателями, их оценку по ряду причин невозможно осуществить ни одним из точных методов. В частности, субъективный характер показателей и отсутствие достаточной статистической базы определяет возможность их приблизительной оценки только с использованием опросных методов.

Для оценки указанных параметров был выбран метод, совмещающий черты статистического опроса и метода экспертных оценок, – экспертный опрос, который оптимально подходит для исследования по ряду причин:

– массовый опрос респондентов неэффективен по причине некомпетентности источников информации, которая в данном случае является определяющим фактором;

– в сравнении с методом экспертных оценок метод экспертного опроса характеризуется бюджетностью и относительной простотой проведения;

– отсутствие проблемы доминирования мнения наиболее авторитетного эксперта, наблюдаемого в методе экспертных оценок;

– возможность осуществить в условиях текущего исследования.

Оптимальная форма исследования, отвечающая всем требованиям и возможностям, – заочное конфиденциальное неанонимное анкетирование с особенностями, учитываемыми при разработке бланков анкет [3]. Отсутствие дискуссионного момента в процессе исследования порождает опас- ность упущения важных идей и увеличивает вес типичных ответов. Один из путей решения проблемы – приведение к каждому из задаваемых вопросов краткого материала в защиту крайних противоположных мнений. Критика или доказательство противоположных точек зрения должны быть равномерными, чтобы не склонить на свою сторону, а стимулировать более глубокий анализ ситуации.

Формирование группы экспертов предлагается проводить методом «шара». Отсутствие узкой направленности рассматриваемых в исследовании вопросов исследования значительно осложняет выбор группы экспертов. Принципиальное значение имеет возможность обеспечения «равноправия» ученых-специалистов различных направлений (экономическая теория и макроэкономика; практическая деятельность в нефтегазовой отрасли, на примере которой проводится исследование; право; аналитика и статистика) с учетом специфики исследуемой проблемы. Метод «шара» необходимо модернизировать с учетом широкой направленности вопросов и заочного способа проведения. Предлагается включить в анкету для каждого из поставленных вопросов дополнительный вопрос о наиболее компетентном специалисте именно в данном вопросе. Конфиденциальность опроса позволит получать пересекающиеся результаты и на основе этого произвести ранжирование мнения каждого специалиста по конкретному вопросу (по статистической частости появления автора мнения в рекомендациях других экспертов). Кроме того, это расширит экспертный круг и позволит получить компетентный результат с экономической, статистической, юридической, математической сторон.

Обработку данных опроса предлагается осуществлять на основе репрезентативной теории измерений. Данная теория направлена на осуществление измерений в качественных шкалах (в которых представляется мнение экспертов) В соответствии с теорией при математическом моделировании реального процесса следует прежде всего установить, в каких типах шкал измерены те или иные переменные. Тип шкалы задает группу допустимых преобразований [7]. Важное значение придается проверке согласованности мнений экспертов и классификации экспертных мнений.

Вычислительный эксперимент

Программа протестирована на практическом примере [5]. Исходные данные для вычислительного эксперимента – данные об объемах предоставленных услуг по обслуживанию газопроводов Златоустовским филиалом ООО «Челябинскрегионгаз» группы потребителей за период с 1 декабря 2006г. по 30 ноября 2009 [1]. Источником статистических данных является «Книга продаж» предприятия. Количество контрагентов предприятия большое, рассматриваются только 3 крупных потребителя:

• •    население Кусы;

• •    население Сатки;

• •    население Златоуста.

Необходимо отметить особенности составления игровых матриц. Стратегии монополиста, как и любой компании, формируются Бюджетом доходов и расходов, который принимается и утверждается в текущем году на будущий. Таким образом, группировку данных для описания стратегий ЗФ ООО «Челябинскреги-онгаз» необходимо проводить по годам (2007– 2009 гг.). Стратегии же потребителей зависят в первую очередь от климатических условий и носят сезонный характер, поэтому группировку данных целесообразно проводить по сезонам года (01.12–28/29.02, 01.03–31.05, 01.06–31.08, 01.09–30.11). На пересечении стратегий игроков расположены выигрыши сторон, а именно – финансовая характеристика объема предоставленных услуг (выручка). Предполагается, что статистика за прошлые периоды содержит в себе информацию о выигрышах сторон при различных стратегиях в ряде аналогичных данной игровых ситуациях и может быть использована для составления текущей платежной матрицы.

По указанным данным с использованием программы были рассчитаны показатели адаптивности (см. рис. 3), на основании которых был сделан вывод о целесообразности гибкого переключения стратегий: оптимальная стационарная стратегия – неэффективна, вложение средств в повышение адаптивности – эффективно.

Заключение

Исследование методов оценки степени адаптивности государства и их программная реализация являются важнейшим этапом разработки методики учета показателей адаптивности при формировании тарифной и налоговой политики государства [10]. На данном этапе важнейшими практическими результатами стали построение системы показателей для оценки степени адаптивности государства и разработка программа для автоматизированного их расчета. Дальнейшая работа с моделью перспективна. Например по результатам аналогичной оценки затрат временных ресурсов можно дать рекомендации по оптимизации срока пересмотра количественных параметров тарифного регулирования по отраслям, налогового законодательства, антимонопольного, земельного законодательства и т.д., указать общее направление этих изменений [4].