Агрегированная модель мультипликативной динамики макроэкономических показателей региона

Исследования в области моделирования макроэкономических процессов на региональном уровне широко представлены в научных трудах. Значительный вклад в развитие направлений, связанных с построением моделей экономического роста, внесли М. Моришима, Р. Столерю, А. Г. Гранберг, А. О. Баранов, Т. Пу, Н. П. Дементьев [1–6]. Значительный вклад в изучение мультипликативных процессов в странах и регионах внесли В. Леонтьев, Р. Миллер, А. А. Широв, А. А. Янтовский, А. С. Булдаев, З. Б.-Д. Дондоков [7–11]. Экспериментальные исследования проводились в области анализа и прогнозирования экономического развития Республики Бурятия [12].

Между тем остаются актуальными исследования в области построения системных мультипликативных моделей регионов с отражением техноло-29

гических факторов в виде влияния коэффициентов материалоемкости и капиталоемкости. Особое значение имеет выявление роли потребительского поведения на динамику основных макроэкономических показателей. Несмотря на ограниченность информационной базы, экспериментальные и методические исследования в этих областях продолжаются.

Для анализа и динамического моделирования регионального воспроизводственного процесса достаточно располагать набором агрегированных показателей валового выпуска, промежуточной и конечной продукции , отраслевые значения которых могут быть получены из данных статического межотраслевого баланса региона, разрабатываемого периодически для определённой территории. Совокупный конечный продукт региона, или валовой региональный продукт, по величине равен объёму валового регионального дохода, используемого на производственное накопление и непроизводственное потребление.

1 Постановка задачи

Рассмотрим статическую линейную модель межотраслевого баланса в разрезе «чистых» отраслей, в каждой из которых производится только один вид продукта или услуги:

X = AX + Y , (1) где X = ( x i ), Y = ( y i ), i = 1, n — векторы валовых выпусков и конечного спроса (конечного продукта) в регионе, n — число «чистых» отраслей или, по терминологии системы национального счетоводства, число видов экономической деятельности; A = ( a ij ), i , j = 1,2,..., n — матрица коэффициентов прямых производственных затрат.

Полагаем, что система (1) продуктивна в силу продуктивности матрицы A , и тогда для любого положительного вектора конечного спроса Y имеется положительное решение, равное

X = ( E - A ) ^{- 1} Y .

На основе данных регионального статического межотраслевого балан -са (1) путем агрегирования можно определять суммарные показатели конечного продукта, равного по стоимости объему валового регионального дохода ( y ), а также валового выпуска ( x ):

nn y= Е y., x=Х x. i=1 i=1

С введением фактора времени t получаем следующие соотношения:

x ( t ) = ax ( t ) + y ( t ) ^ x ( t ) = g • y ( t ), (2) где a — материалоёмкость валового выпуска, g = (1 - a ) ^-1— мультипликатор валового выпуска .

Величины материалоемкости и мультипликатора также могут быть функциями времени: a = a(t), g = g(t). Для простоты в нашем анализе рассмотрим ситуацию, когда данные показатели являются постоянными на всем протяжении прогнозируемого периода (a,g - const). Они равны их расчетным значениям в начальном периоде на основе отчетных данных межотраслевого баланса:

x (0)      g - 1 x (0) - y (0)

g -, a --.

y (0)        g       X (0)

Основными частями регионального конечного продукта, используемыми за определенный период времени, являются накопление основных производственных фондов ( и ) и непроизводственное потребление ( c ):

у ( t ) - и ( t ) + c ( t ).

В свою очередь,

и ( t ) - s ( t ) • у ( t ), c ( t ) - у ( t ) - и ( t ) - у ( t ) - s ( t ) • у ( t );

c(t)- (1 - s (t)) • у(tb где s(t) — норма сбережений (или норма накопления) в периоде t.

Динамика конечного продукта, следовательно, и регионального дохода, определяется характером динамики производственного накопления и непроизводственного потребления .

Исходя из содержательных понятий динамика совокупного производственного накопления представляется следующим образом:

, ,    , dx ( t )

и (t) - b—, dt где b — капиталоёмкость валового выпуска (предельное отношение производственного накопления к приросту валового выпуска). Тогда

, , , dx ( t )      , ,

у ⁽ t ) ^{- b} j ^{+ c (} t ^).

dt

Ы                           dx ( t )      dy ( t )

.

Из условия (2) следует: —— - g dt dt

, dy ( t )      b dy ( t )

.

Соответственно и(t) - bg ---— dt 1 - a dt

Обозначим: в - bg - b(1 - a) 1, тогда и(t) - в dy^t!, dt где p — капиталоемкость валового регионального дохода.

В результате получаем агрегированные модели динамики регионального дохода и валового выпуска в виде линейных неоднородных дифференциальных уравнений первого порядка:

у ( t ) = в dyp- + c ( t ), dt

, ,      1 (, dx ( t )      , .^ _nXx ( t )         , ,

x ⁽ t ) = -—I b—^{1 + c (} t ) 1 = ^в~— ⁺ g • c ⁽ t )•

1 - a ^ Xt J Xt

2 Вывод уравнений динамики макропоказателей

На первом этапе решаем однородное уравнение у ( t ) - в

Xy ( t ) dt

= 0 ме

тодом разделения переменных:

Xy ( t ) У ⁽ t )

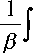
1 t

Xt ^ у ( t ) = у (0) e ^в •

Обозначим: 8 = — =---• Коэффициент 8 есть темп технологическо- в b го прироста — максимально допустимый темп прироста, определяемый коэффициентами материалоемкости (a) и капиталоемкости (b) валового выпуска.

В результате получаем уравнение динамики регионального дохода при гипотетическом отсутствии потребления

у ( t ) = у (0) e ^{8 t} •

На втором этапе ищем частное решение уравнения (4), допуская естественное предположение о наличии непроизводственного потребления. Используя метод вариации произвольной постоянной, после преобразований получим следующее уравнение динамики регионального дохода:

у ( t ) = ( -8 j c ( t ) e ^{-8 t}Xt ) e ^{8 t} .                                (5)

Зададим характер динамики непроизводственного потребления. Предположим, что непроизводственное потребление увеличивается с некоторым непрерывным темпом прироста r :

c ( t ) = c (0) e r •

Подставим эту функцию в уравнение (5) и после преобразований получим следующее уравнение:

у ( t ) = ⁽ у (0) -       c (0) ] e ^{8 t} + ⁸ c (0) e^rt •                              (6)

^      8 - r J 8 - r

Соответственно получаем уравнение производственного накопления: u (t) = У (t) — c (t) или u (t) = 1 У(0) -

8 - r

c (0) I e ^{8 t} +

r

8 - r

c (0) e r .

Темп прироста непроизводственного потребления r как экзогенная величина может задаваться для проведения сценарных прогнозных расчетов, играя роль управляющего параметра для мультипликативной модели динамики основных макропоказателей. Для более наглядной демонстрации влияния темпа прироста r на макроэкономическую динамику преобразуем первый сомножитель в выражениях (6) и (7) с учетом (3) для t = 0 :

у (0) - ⁸ c (0) = у (0) ^[ 1 - ^{8 8} ] = у (0) [ 1 - ⁸ (1 - s (0)) ¹ =

8 - r ^ 8 - ry(0) J 8 - r J

= ^ rу (0).

8 - r

Обозначим: r = 8 • s (0) . Тогда вместо (6) и (7) получаем следующие уравнения:

У (t) = —У (0) e8t + — c (0) er = —у( t) + — c (t),(8)

8 - r        8 - r        8 - r

• u (t) = —у (0) e8t + —c (0) er = —у( t) + —c (t).(9)

8 - r        8 - r        8 - r

Таким образом, динамические функции основных макропоказателей определяются, с одной стороны, макроэкономическими технологически-

• <             [е 1 - a I„

ми факторами I 8 =----I, с другой стороны, поведенческими предпочте-\ b J ниями совокупного потребителя, то есть величиной нормы сбережений в базовом периоде s(0) и темпом прироста непроизводственного потребления r.

3 Функции абсолютного и относительногоприроста макропоказателей

Рассмотрим непрерывные функции абсолютного прироста основных макропоказателей:

dy ( t )   ef r - r

------= о I ------ dt ^ 0 - r

У (0) e ° +

—o (0) e r 1 = 0 • u ( t ), о - r )

y '( t ) = 0 • u ( t );

du ( t ) dt

= u'(t) = (y (t) - o (t))' = y'(t) - o'(t) = 0 • u (t) - r • o (0) er, u'(t) = 0 • u (t) - r • o (t), а также непрерывные функции относительного прироста основных макропоказателей:

P y ⁽ t ) =

t ^: = 0 ^ = 0 • s ( t ), y ⁽ t )       y ⁽ t )

P u ⁽ t ) =

u '( t ) u ( t )

⁰ • ^{u (} t ) ^{- r} • ^{o (} t )        °C ⁽ t )       J ^- s ⁽ t )

-------------= 0 - r ---= 0 - r------ u ( t )                  u ( t )             s ( t )

Очевидно, что темпы прироста региональных доходов и накоплений прямо пропорциональны динамике нормы сбережений, для которой допускаем реальные экономические ограничения: 0 <  s ( t ) <  1 ^ p _y ( t ) <  0 . Отметим, что с повышением нормы сбережений удельный вес потребительских расходов в общем региональном доходе при этом неуклонно па -дает.

Рассмотрим подробнее характер динамики макропоказателей. Для начального периода времени предполагаем, что

0 <  s (0) <  1, y (0) >  o (0) >  0.

В дальнейшем темпы прироста макропоказателей зависят от значений темпа прироста потребительских расходов p _o ( t ) = r . Прежде всего предположим, что непроизводственное потребление со временем не снижается, то есть r >  0. При этом возможны различные случаи:

• 1)    r = 0 ^ o ( t ) = o (0) = oonst . Динамика макропоказателей в этом случае определяется формулами:

u (t) = s (0) • y (0) est = s (0) • y( t) = u (0) e°, y (t) = s (0) • y (0) e0t + o (0) = u (t) + o (0);

du(t) dy(t)    _    . .    _                 ~ x

-j— = —;— = ⁰ • ^{u (} t ) = ⁰ • ^{s (0)} • y ⁽ t ) = ^r • y ⁽ t );

dt dt

/ \ р \ е 1 — a

P c ( t ) = r , P u ( t ) = 3 - b

P, ( t ) = 3 ^ = r^ . y          y ( t ) y ( t )

При постоянном темпе прироста производственного накопления ожидается монотонно возрастающая динамика регионального дохода. В любом случае при малых значениях r или при r ^ 0 доля потребления в региональном доходе при t ^» уменьшается до нуля, соответственно норма сбережения s ( t ) ^ 1, а фактические темпы прироста регионального дохода и производственного накопления увеличиваются, приближаясь к значению технологического темпа прироста: p _y ( t ) ^ 3 , p _u ( t ) ^ 3 .

• 2)    r = r = 3 s (0) ^ c ( t ) = c (0) • e^{3s (0) t} . Ожидается следующая динамика макропоказателей:

  У ⁽ t ) =

  
  
  
  

  3 - r

  
  

  c (0) e r =      \_йc (0) e^rt = c “’’ e^r t = y (0) e^{s (0)} t ,

  3 ( 1 - s (0) )           1 - s (0)

  
  

u ( t ) =        c (0) e^rt = s ^⁰)- c (0) e^t = u (0) e ⁽⁰⁾ t ;

3 - r 1 - s (0)

, _y   u ( t )    u (0) e^r t     u (0)

s(t) =      = v ’ ■ =      = s(0);

y ( t )    y (0) e^r t    y (0)

1 — a

P c ( t ) = P y ( t ) = P u ( t ) = 3 • s (0) = — s (0) = r. b

В данном случае экономическая динамика происходит с постоянной нормой накопления, равной ее первоначальному значению, а непрерывные темпы прироста для всех показателей одинаковые и определяются постоянными значениями материалоемкости, капиталоемкости и нормы сбережений.

При отклонениях r от r наблюдается разная динамика всех показателей (таблица 1). Причём в случаях r >  r существует максимальный временной период ( t = t *), до которого происходит экономический рост; после этого момента времени начинаются спад объёмов производства и последующая деградация экономической жизни региона.

. dy ( t ) _Л _

Значение t определяется путем решения уравнения:----= 0 или dt

3 | y (0) -

c(0) |e3t + r '' c(0)er = 0, 3 - r )      3 - r откуда

*      1 , r - r • s (0)

t =---In-----—

5 - r r - 5 • s (0)

1 _ln r ( 1 - s (0) )

5 - r r - r

Таблица 1

Динамика основных макроэкономических показателей: рост ( Z ) , снижение ( ] ) .

Макропоказатели	Темпы прироста непроизводственного потребления: P c ( t ) = r .
	r = 0 ( t ^» )	0 <  r <  'r	r = r	r >  r ( t <  t *)
У ( t )	Z	Z	Z	Z
и ( t )	Z	Z	Z	> 0, ]
c ( t )	= c (0)	Z	Z	Z
P y ( t )	= 5 u ( t ) У ( t )	Z	= r	> 0, ]
P u ( t )	= 5	Z	= r	< 0
P c ( t )	= 0	= r	= r	= r
S ( t )	Z	Z	= s (0)	]
С ( t ) u ( t )	]	]	= c (0) = 1 - s (0) = u (0) = s (0)	Z

4 Пример расчета динамики макропоказателей

Рассмотрим пример, основанный на расчетных данных реальной экономической системы одного из сибирских регионов (в условных денежных единицах).

Дано:

X (0) = £ x (0) = 2881; y (0) = £ y (0) = 1406; b = 1.627; s (0) = 0.214 . i = 1                                                  i = 1

Расчетные коэффициенты b , s (0) являются результатами статистических исследований.

Вычисление коэффициентов и макропоказателей:

g = x ^ * 2.049, a = g 1 * 0.512; в = — * 3.334; 5 = — * 0.3(30%);

y(0)              g              1 - a             в r = 5 • s(0) * 0.0642(6.42%);

ax (0) * 1475; x (0) = ax (0) + y (0) * 2881;

u (0) = s (0) • y (0) * 301; c (0) = (1 - s (0)) • y (0) = 0.786 y (0) * 1105.

y (0) = u (0) + c (0) = 1406.

Уравнения динамики y ( t ), u ( t ), c ( t ) имеют вид:

y ( t ) = y (0) • e °,³ t * 1406 - 1,35 t , c ( t ) = c (0) • e r = 1105 • e r ,

0 064 —r.03

y (t) = 006--1406-1,35t + -0.3--1105 - ert,(8')

0.3 - r               0.3 - r

u(t) = 0.064 r -1406 -1,35t + —--1105 - ert.(9')

0.3 - r                0.3 - r

Темпы прироста макропоказателей: pc (t) = r (задается для сценарных расчетов), p (t) = 0,3 u^- = 0,3 - s(t), pu (t) = 0,3 - r cQ = 0,3 - r ^st).

^y           y ( t )                    u                 u ( t )               s ( t )

Характер динамики всех макропоказателей зависит от значений темпа прироста непроизводственного потребления.

Рассмотрим два предельных случая: r = r ; r >  r.

• 1)    r = r = 0.0642. Следует ожидать монотонный рост всех трех макропоказателей с темпом прироста, равным 6.42%, постоянной нормой сбережений и постоянным соотношением потребления и накопления:

c ( t ) = c (0) e ⁰’^{0642 1} * 1105 - 1.0663 ^t ,

y ( t ) = y (0) e^0.0642t * 1406 - 1.0663 t , u ( t ) = u (0) e^0.0642t * 301 - 1.0663 t ,

s ( t ) = u^ = u⁰- = s (0) * 0.214, ct ) = c ⁰- = 1- s (°- * 3.673, У ( t ) У (0)                    u ( t ) u (0) s (0)

,, u ( t ) u (0) e r‘    u (0)

s (t) = -— = ——— =    = s (0);

y ( t ) y (0) e^rt y (0)

P c ( t ) = P y ( t ) = P u ( t ) = r * 0.0642.

• 2)    r = 0.08(8%) >  r. Рассчитаем предельный срок экономического роста

  *

  t

  
  

1 _ln°»⁷⁴ (1 - ^0.214

------------In------------------ * 7.88. 0.3 - 0.074   0.074 - 0.0624

В период t <  t* ожидается замедляющийся рост выпуска и регионального дохода с падением темпов прироста, рост потребительских расходов, сопровождающийся неуклонным снижением объемов производственного накопления и нормы сбережений. В дальнейшем при t >  t * начнется снижение объемов производства, а продолжающийся рост непроизводственного потребления будет вызывать «проедание» накоплений (отрицательные значения нормы сбережений) и отсутствие экономических перспектив.

Заключение

Для моделирования региональных воспроизводственных процессов достаточно иметь сводные макроэкономические показатели, определяемые на основе данных отчётных межотраслевых балансов, периодически разрабатываемых в регионах. Агрегированная модель макроэкономической динамики формируется в виде дифференциального уравнения, учитывающего как процессы производственного накопления, так и рост непроизводственного потребления, темп которого является управляющим параметром. В конечном счёте характер динамических процессов в региональной экономической системе в значительной степени зависит от технологических значений материалоёмкости и капиталоёмкости, нормы сбережений и темпа роста непроизводственного потребления.