Агрегированная производственная функция с учетом научно-технического прогресса для экономики России

Автор: Гребнев М.И.

Журнал: Вестник Пермского университета. Серия: Экономика @economics-psu

Рубрика: Экономико-математическое моделирование

Статья в выпуске: 4 (27), 2015 года.

Бесплатный доступ

Рассматривается проблема агрегирования производственных функций как моделей производственных процессов на региональном и национальном уровнях экономики России. Проблема агрегирования была впервые сформулирована в 40-е гг. XX в. на страницах журнала Econometrica, однако остается нерешенной до сих пор. Данная задача является частной в рамках более широкого направления исследований, связанного с изучением «мостов» между микро- и макроэкономикой. Развивается статистический метод агрегирования производственных функций, предложенный пермской школой иерархического анализа экономики. Цель работы состоит в адаптации данного метода агрегирования для экономики России. Предлагается модификация метода для случая неравномерности распределения ресурсов между элементами экономики. В работе представлены оценки параметров «инвестиционной» производственной функции Кобба - Дугласа для всех регионов России. На основе региональных производственных функций осуществлен синтез агрегированной производственной функции для экономики России. При построении агрегированной производственной функции учитывается фактор научно-технического прогресса. Оценки параметров агрегированной производственной функции для экономики России получены на базе программного комплекса «ПРОГНОЗ. СБСП СЭР». Установлено, что выведенная производственная функция обеспечивает более точные прогнозы по сравнению с традиционной макроэкономической производственной функцией Кобба - Дугласа. На основании агрегированной производственной функции получена оценка ВВП России на 2015 г., построен прогноз на 2016-2018 гг. и проведен анализ производственных процессов в экономике России: рассчитаны коэффициенты эластичности по факторам производства, предельная норма замещения и эластичность замещения между факторами производства. Согласно полученному прогнозу в 2015 г. по базовому сценарию в России ожидается спад экономики на 2,6%, в 2016-2018 гг. экономика начнет восстанавливаться, темпы экономического роста составят 2-2,5% в год.

Еще

Производственная функция, статистический метод агрегирования, региональный и национальный уровни экономики

Короткий адрес: https://sciup.org/147201504

IDR: 147201504

Текст научной статьи Агрегированная производственная функция с учетом научно-технического прогресса для экономики России

Публикации Л. Кляйна [10; 11] в журнале Econometrica в 1946 г. породили серию статей, касающихся проблемы агрегирования производственных функций. Шу Шан Пу четко сформулировал основную проблему агрегирования производственных функций – необходимо найти такую функцию, в которой совокупный выпуск зависел бы только от совокупных затрат факторов производства, но не от их распределения между фирмами [15] . По мнению Л. Кляйна, агрегированная производственная функция отражает технологические процессы. Другой точки зрения придерживался К. Мэй: агрегированная производственная функция отражает процессы принятия решений [12; 13] .

А . Натаф сформулировал условия агрегирования производственных функций [14] : агрегированная производственная функция существует только тогда, когда ПФ является аддитивносепарабельной, то есть когда представима в виде f(k,l) = ф(к) + ф(Г).

Ф. Фишер [9] отметил, что условия А. Натафа очень жесткие. Опираясь на аргументы К. Мэя и интерпретируя производственную функцию как максимально возможный объем производства при заданных затратах ресурсов, он сформулировал собственные условия существования агрегированной производственной функции – одинаковые для всех фирм пропорции выпуска продукции.

В данной работе предложен краткий обзор методов агрегирования производственных функций, более полный обзор представлен в работе [1] .

В 2000-х гг. в г. Перми под руководством профессора Ю.К. Перского была создана научная школа иерархического анализа экономики. В 2008 г. Д.Н. Шульцем был предложен статистический метод агрегирования ПФ [6] . Уникальность метода и его практическая значимость была подтверждена членом-корреспондентом РАН Г.Б. Клейнером после представления результатов на семинаре «Проблемы моделирования производственных систем» в Центральном экономикоматематическом институте РАН.

Результаты построения агрегированной производственной функции для экономики России на основании отраслевых производственных функций представлены в работе [3] .

Теоретические положения и выводы, содержащиеся в работе, вносят вклад в исследование актуальных вопросов теории агрегирования производственных функций.

Практическая значимость работы заключается в возможности использования результатов исследования органами исполнительной власти РФ для построения агрегированных производственных функций, расчета краткосрочных и среднесрочных прогнозов ВВП России, оценки чувствительности объема ВВП России к изменению объемов факторов производства.

С точки зрения статистического метода агрегирования каждая микроэкономическая производственная функция рассматривается как случайная реализация статистической модели

Yt = f^.x), (1)

где i = 1, ...,n , n – количество элементов в экономической системе, X – объем затраченных ресурсов, ^i – технологические параметры. Они являются независимыми и одинаково распределенными случайными величинами.

Макроэкономическая производственная функция определяется как математическое ожидание данной реализации:

- для случая интенсивных факторов (*1 = *2 = - = X_n ):

P f ~

Y ^nM[y} = n f(a,x)g(a)da = nF(x), (2)

где Y = ^_1У1 , g(a) – функция плотности распределения параметра CL , F – «средняя» производственная функция;

- для случая экстенсивных факторов ( x = Z"=1 Xi ):

Y ~ n ^ f ^a,—^ g(a)da = nF (—). (3)

Данный функционал предполагает равномерное распределение ресурсов между элементами экономики, в случае высокого уровня неравномерности распределения ресурсов предлагается использовать следующее выражение:

У(Х) ^{= n} $ f(a,wX)g(d)g(w)dadw, (4)

где w – весовые коэффициенты, Xi = w_tX ;

gM – функция плотности распределения параметра w .

Для вывода функциональной формы агрегированной производственной функции с учетом научно-технического прогресса (НТП) для экономики России на региональном уровне будем использовать «инвестиционную» производственную функцию Кобба – Дугласа с учетом НТП:

у = Ае^лЧ^аР, (5)

где У – валовой региональный продукт (ВРП) в ценах 1998 г., млн руб.;

i – инвестиции в основной капитал по региону в ценах 1998 г., млн руб.;

l – фонд оплаты труда по региону в ценах 1998 г., млн руб;

t – время.

Использовать инвестиции в качестве основного фактора производства для случая переходной экономики России предложил В.А. Бессонов в работе «Анализ динамики российской переходной экономики» [2] . По мнению В.А. Бессонова, «инвестиции являются дефицитным фактором в переходной экономике» и «применительно к ним не существует проблемы выделения эффективно используемой части, в отличие от данных по фондам и труду» [2, с. 50]. Высокую точность аппроксимации «инвестиционной» производственной функцией отмечает И.Г. Поспелов [7, c. 141].

Для оценки параметров линеаризуем производственную функцию Кобба – Дугласа с помощью логарифмического преобразования:

Ln(y) = ln(A) + At + aln(i) + pin(l\ (6)

Оценки параметров региональных производственных функций по 83 субъектам РФ представлены в табл. 1. Для получения оценок использовались данные Федеральной службы государственной статистики. Оценки получены с помощью платформы бизнес-аналитики PrognozPlatform7 [5] .

Таблица 1

Оценки параметров региональных производственных функций (с учетом НТП)

Субъект РФ	In^A)	A	a	p	A -\- cc -\- p
Белгородская область	8.11	0.050	0.12	0.11	0.28
Брянская область	7.55	0.024	0.04	0.25	0.31
Владимирская область	7.78	0.015	0.11	0.16	0.29
Воронежская область	8.23	0.022	0.11	0.14	0.27
Ивановская область	7.64	0.012	0.09	0.15	0.25
Калужская область	7.20	0.032	0.16	0.13	0.29
Костромская область	7.43	0.016	0.09	0.18	0.28

Продолжение табл. 1

Субъект РФ	IntA)	Л	a	p	A + ot + fi
Курская область	7.33	0.021	0.11	0.25	0.38
Липецкая область	7.60	0.011	0.10	0.23	0.34
Московская область	7.81	0.028	0.22	0.17	0.42
Орловская область	6.72	0.004	0.12	0.28	0.41
Рязанская область	7.92	0.020	0.13	0.10	0.23
Смоленская область	6.77	0.019	0.20	0.20	0.42
Тамбовская область	7.74	0.023	0.10	0.14	0.27
Тверская область	8.07	0.020	0.01	0.26	0.29
Тульская область	7.09	0.013	0.13	0.26	0.40
Ярославская область	7.43	0.018	0.11	0.27	0.39
г. Москва	5.34	0.021	0.59	0.10	0.69
Республика Карелия	7.03	0.00	0.18	0.17	0.35
Республика Коми	8.21	0.006	0.09	0.20	0.29
Архангельская область	7.23	0.025	0.12	0.29	0.43
Ненецкий АО	6.65	0.038	0.13	0.43	0.60
Вологодская область	8.21	0.001	0.13	0.15	0.27
Калининградская область	6.84	0.030	0.12	0.23	0.38
Ленинградская область	6.02	0.020	0.18	0.38	0.59
Мурманская область	9.39	0.00	0.00	0.11	0.11
Новгородская область	7.91	0.022	0.08	0.12	0.22
Псковская область	7.53	0.014	0.14	0.07	0.22
г. Санкт-Петербург	8.15	0.034	0.15	0.22	0.41
Республика Адыгея	6.46	0.038	0.16	0.11	0.27
Республика Калмыкия	5.63	0.003	0.23	0.08	0.32
Краснодарский край	8.05	0.022	0.14	0.21	0.37
Астраханская область	6.46	0.012	0.21	0.21	0.43
Волгоградская область	7.41	0.0003	0.20	0.19	0.39
Ростовская область	6.93	0.024	0.23	0.23	0.49
Республика Дагестан	6.30	0.043	0.15	0.29	0.48
Республика Ингушетия	5.76	0.008	0.11	0.16	0.28
Кабардино-Балкарская Республика	7.06	0.029	0.00	0.34	0.37
Карачаево-Черкесская Республика	6.66	0.030	0.05	0.23	0.31
Республика Северная Осетия-Алания	6.62	0.021	0.14	0.17	0.33
Чеченская Республика	4.23	0.00	0.33	0.36	0.70
Ставропольский край	7.79	0.024	0.10	0.25	0.38
Республика Башкортостан	8.77	0.038	0.09	0.18	0.30
Республика Марий Эл	7.41	0.025	0.14	0.05	0.22
Республика Мордовия	6.65	0.020	0.19	0.19	0.40
Республика Татарстан	7.82	0.020	0.20	0.19	0.41
Удмуртская Республика	7.84	0.010	0.11	0.19	0.30
Чувашская Республика	6.65	0.001	0.24	0.15	0.39
Пермский край	7.73	0.019	0.25	0.12	0.39
Кировская область	8.91	0.011	0.07	0.04	0.12
Нижегородская область	8.62	0.018	0.08	0.21	0.31
Оренбургская область	7.46	0.019	0.19	0.17	0.39
Пензенская область	7.82	0.026	0.14	0.07	0.24
Самарская область	7.86	0.001	0.21	0.19	0.40
Саратовская область	7.65	0.025	0.20	0.13	0.36
Ульяновская область	8.19	0.017	0.10	0.12	0.23
Курганская область	7.12	0.009	0.14	0.19	0.34
Свердловская область	7.68	0.019	0.20	0.22	0.44
Тюменская область	8.71	0.020	0.01	0.39	0.42
Ханты-Мансийский АО	10.24	0.028	0.00	0.33	0.35
Ямало-Ненецкий АО	9.70	0.011	0.09	0.15	0.25
Челябинская область	6.84	0.011	0.32	0.13	0.47
Республика Алтай	6.08	0.011	0.15	0.14	0.30
Республика Бурятия	7.71	0.015	0.07	0.19	0.28
Республика Тыва	6.99	0.019	0.005	0.14	0.17
Республика Хакасия	8.58	0.019	0.01	0.06	0.09
Алтайский край	7.27	0.013	0.19	0.18	0.39
Забайкальский край	7.96	0.032	0.12	0.09	0.25
Красноярский край	9.18	0.021	0.06	0.19	0.27
Иркутская область	8.82	0.031	0.14	0.10	0.27
Кемеровская область	8.36	0.007	0.10	0.20	0.31
Новосибирская область	7.58	0.013	0.19	0.20	0.40
Омская область	7.26	0.020	0.25	0.14	0.41

Окончание табл. 1

Субъект РФ	ln(A)	A	a	p	A + ot + fi
Томская область	7.85	0.011	0.03	0.31	0.35
Республика Саха (Якутия)	8.97	0.018	0.08	0.12	0.21
Камчатский край	8.84	0.014	0.02	0.05	0.08
Приморский край	8.57	0.017	0.12	0.12	0.25
Хабаровский край	7.73	0.005	0.14	0.22	0.36
Амурская область	8.45	0.021	0.10	0.05	0.18
Магаданская область	8.38	0.000	0.00	0.09	0.09
Сахалинская область	6.82	0.050	0.06	0.33	0.44
Еврейская АО	6.09	0.029	0.08	0.18	0.29
Чукотский АО	4.66	0.014	0.14	0.53	0.68

На основании критерия согласия Колмогорова – Смирнова можно сделать вывод о том, что для параметров л, а , Р производственной функции у = Ае^лЧ^а10 характерен нормальный закон распределения

(Л: К - S р - value ¹ = 0,57; а: К - S р - value = 0,22; 0: К - S р - value = 0,47).

При построении агрегированной производственной функции с учетом НТП будем предполагать региональную структуру экономики России однородной на периоде моделирования. Поэтому в качестве весовых коэффициентов ( Wj и W^ ) будем брать их средние значения на временном периоде

( 2012 ч

^ wi[t] у 15;

t=1998

\t=1998 /

На основании критерия согласия Колмогорова – Смирнова можно сделать вывод о том, что для параметров Wf и W^ наиболее подходящей является функция логнормального распределения ( wp К - S p - value = 0,98; w_L: К - S p - value = 0,75):

W^LogN^— 0.3 661,1.0644);

Таким образом, агрегированная производственная функция с учетом НТП будет иметь следующую функциональную форму:

Yapf_ntp

= nM[A]eMWt+la2Wt2;

* J LogN(p[w;],a[^^^ , (9)

* J LogN(p[wMw^^^^

где ^APFUTP – валовой внутренний продукт (ВВП) в ценах 1998 г., млн руб.;

I – инвестиции в основной капитал по России в ценах 1998 г., млн руб.;

L – фонд оплаты труда по России в ценах 1998 г., млн руб.

В качестве оценок параметров Wj , ^L возьмем значения параметров из полученных теоретических функций распределения (8).

Для оценки параметров МЩ , <т[л] , M[a] , c[«], A^ E^^ ] , a[p] функции (9) использовался метод наименьших квадратов:

Вероятность ошибки при отклонении нулевой гипотезы о виде закона распределения параметра (ошибки первого рода) по критерию Колмогорова – Смирнова.

2012 z 4 ?

\ 1 (---—» W /

A mt-ii rt-i/ t=1999 x L J 7

В результате были получены следующие оценки параметров: ri = 79 2; M[A] = 3412,47; ^M = —0,3661; a[w_z] = 1,0644; ^[w_L] =

-0,2810; a[wl] = 1,0124; М[Л] = 0,0118; сг[Л] — 0,0063; M[a] = 0,1985; cr[a] = 0,0901; M[0] = 0,0802 ; = 0,0112. Оценки параметров были получены с помощью программного комплекса «ПРОГНОЗ. СБСП СЭР – система балансировки стратегических прогнозов социальноэкономического развития Российской Федерации, ее регионов и отраслей» [4] .

Графики агрегированной производственной функции с учетом НТП (при фиксированном значении t =15, 2012 г.) и ее линий уровня (изоквант) представлены на рисунках ниже (рис. 1, 2).

Рассчитаем ключевые характеристики для полученной агрегированной производственной функции с учетом НТП:

- Коэффициенты эластичности ВВП по факторам производства:

eO',!') = 0,27; ₍₁₁₎

e(Y, L) = 0,08.

Эластичность ВВП по инвестициям показывает, что при изменении объема инвестиций в основной капитал на 1% объем ВВП изменится на 0,27%. Эластичность ВВП по фонду оплаты труда показывает, что при изменении фонда оплаты труда на 1% объем ВВП изменится на 0,08%.

- Предельная норма замещения агрегированной производственной функции:

^s^t^^u- (12)

Данное значение предельной нормы замещения s говорит о том, что объем инвестиций в основной капитал I необходимо увеличить на 2,1 млн руб. при уменьшении фонда оплаты труда L на 1 млн руб., чтобы при этом величина ВРП осталось неизменной.

- Эластичность замещения агрегированной производственной функции с учетом НТП:

e(I,L) = 0,189 . (13)

² При построении агрегированной производственной функции не учитывались Ненецкий автономный округ, Ханты-Мансийский автономный округ, Ямало-Ненецкий автономный округ, так как данные регионы входят в состав областей, и Чеченская Республика, по которой отсутствуют статистические данные на период 1998–2004 гг.

Данное значение эластичности замещения говорит о том, что для увеличения предельной нормы замещения s на 1% необходимо увеличить

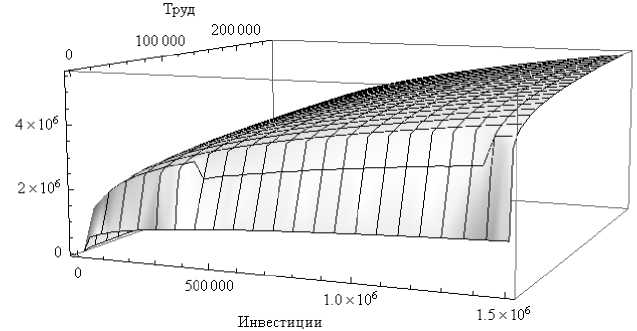
Рис. 1. Агрегированная производственная функция с учетом НТП для экономики России

отношение между инвестициями в основной капитал и фондом оплаты труда U/L) на 0,189%.

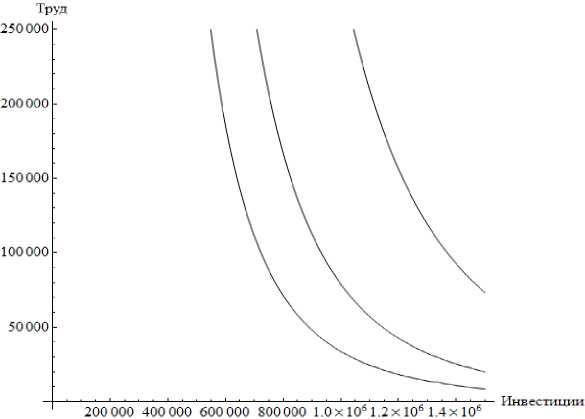
Рис. 2. Изокванты агрегированной производственной функции с учетом НТП для экономики России

График фактической динамики ВВП Рос-

сии и модельной динамики представлен на рис. 3.

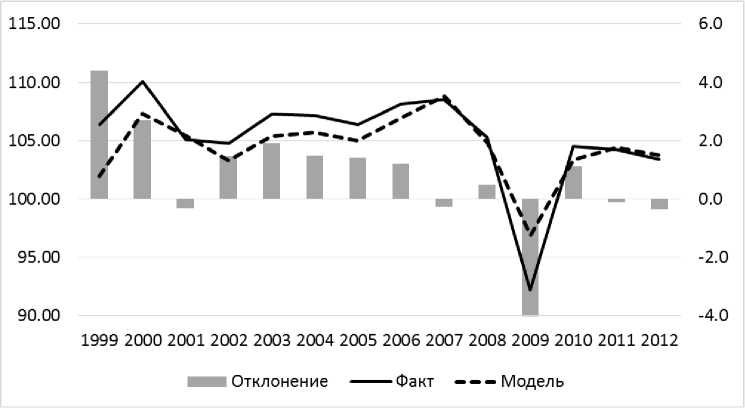
Рис. 3. Модельный ( Yapf_ntp ) и фактический ряд

Сравним качество агрегированной производственной функции, полученной с помощью статистического метода агрегирования (9), с качеством регрессионной модели в форме производственной функции Кобба – Дугласа:

Ycd_ntp ⁼ Ae^ l^a L^ £ , (14)

где £ – случайный член. Так как между факторами имеет место Для этого оценим параметры модели (14) в сильная корреляция (табл. 2), для получения оце- линеаризованной форме: нок использовалась ридж-регрессия. Статистиче- Iti^Ycd ntp^) ~ Iti(A') “h At “H ccIti^T) “H ^ItiXIj') ские характеристики и оценки параметров модели E ⁽¹⁵⁾ (15) представлены в табл. 3. Таблица 2 Коэффициенты корреляции
Показатель		I		L		t
I		1,00		0,99		0,98
L		0,99		1,00		0,97
t		0,98		0,97		1,00
Таблица 3 Результаты оценивания производственной функции Кобба – Дугласа с учетом НТП для экономики России
Коэффициент регуляризации ridge = 0,05. Коэффициент детерминации R² = 0,984. Скорректированный коэффициент детерминации AdjustedR² = 0,959. F -статистика F = 110,69. p -значение p = 0,00 I
Показатель	Коэффициенты		Стандартная ошибка		t-статистика	p-значение	VIF*
ln(Aj	9,84		1,05		9,32	0,00
Л	0,01		0,01		1,34	0,21	3,18
a	0,26		0,10		2,71	0,02	2,46
p	0,15		0,08		1,78	0,10	2,78
*VIF ( variance inflation factor) – коэффициент возрастания дисперсии.

Результаты сравнения качества аппрокси- средней ошибки аппроксимации (E± и ^2 ) представ- мации моделей (9) и (14) на основании скорректи- лены в табл. 4.

рованного коэффициента детерминации ( Adj R² ) и

Таблица 4

Сравнение моделей (9) и (14) 3

Год		Y[t] Hr-if¹⁰⁰		YcdntpW . v--- *CD NTp\t ^— 1J	YapfntpW . v-------iT * 100 *APF NTP\1 ^— 1J
1999		106,4		98,8	102,0
2000		110,0		108,6	107,3
2001		105,1		106,6	105,4
2002		104,7		104,3	103,3
2003		107,3		106,0	105,4
2004		107,2		106,2	105,7
2005		106,4		105,7	105,0
2006		108,2		107,6	107,0
2007		108,5		109,7	108,8
2008		105,2		105,3	104,8
2009		92,2		96,7	96,9
2010		104,5		103,6	103,4
2011		104,3		104,3	104,4
2012		103,4		104,1	103,8
Adj R²				0,52	0,66
n i = l	Yj-Yt Yi		* 100%	1,514	1,507
1 Я? ⁼ - * у A	n			2,39	1,99

³ – ВВП в ценах 1998 г. в текущем периоде, млн руб. (факт);

Y[t-1] – ВВП в ценах 1998 г. в предыдущем периоде, млн руб. (факт);

Ycd_ntp [^f] – ВВП в ценах 1998 г. в текущем периоде, млн руб. (модель (14)) ;

Ycd_ntp [^{f —} 1] – ВВП в ценах 1998 г. в предыдущем периоде, млн руб. (модель (14)) ;

Yapf_ntp И – ВВП в ценах 1998 г. в текущем периоде, млн руб. (модель (9)) ;

Yapf_ntp [^{f —} 1] – ВВП в ценах 1998 г. в предыдущем периоде, млн руб. (модел ь(9)) .

Средняя ошибка аппроксимации агрегированной производственной функции ниже, чем у регрессионной модели в форме производственной функции Кобба – Дугласа ( ниже на 0,007%, ниже на 0,4%), а значение скорректированного коэффициента детерминации выше.

Результаты верификации моделей (9) и (14) на временном отрезке 2013–2014 гг. представлены в таблицах ниже (табл. 5, 6) .

Таблица 5

Верификация модели (9)

Показатель	2013 г.	2014 г.
Y[t]/Y[t - 1]	101,3	100,6
Yapp ntpN/W ntp[^ ^— 1]	101,9	100,6
(Y[t]/Y[t — 1]) — (Y_APF__NTp[t]/Y_App__NTp[t — 1])	–0,6	0,0

Таблица 6

Верификация модели (14)

Показатель	2013 г.	2014 г.
Y\t~\/Y\t-1]	101,3	100.6
YcD NTp{Y]/YcD NTp[t ^— 1]	102,1	100,6
(X[t]/Y[t — 1]) — (Y_CDNTp[t]/Y_CD__NTP[t — 1])	–0,8	0,0

Точность прогноза, полученного с помощью агрегированной производственной функции на 2013 г. выше точности прогноза, полученного с помощью регрессионной модели в форме производственной функции Кобба – Дугласа, на 2014 г.; модели (9) и (14) имеют одинаковую точность прогнозирования.

Результаты верификации и статистические характеристики моделей (9) и (14) свидетельствуют о том, что агрегированная производственная функция с учетом НТП имеет высокую точность, срав- нимую с точностью регрессионной модели в форме производственной функции Кобба – Дугласа.

Согласно агрегированной производственной функции с учетом НТП по базовому сценарию в 2015 г. ожидается сокращение ВВП России на 2,6%, а начиная с 2016 г. экономический рост восстановится и на периоде 2016–2018 гг. будет составлять 2–2,5% (табл. 7) . По оптимистическому сценарию спад ВВП в 2015 г. составит 2%, а на периоде 2016–2018 гг. темпы роста будут находиться в районе 3% (табл. 7) .

Таблица 7

Прогноз ВВП России на основании агрегированной производственной функции с учетом НТП

Показатель	Факт	Оценка	Прогноз
Показатель	2014 г.	2015 г.	2016 г.	2017 г.	2018 г.
ИФО ВВП ( )
Вариант 1	100,6	97,4	102,3	102,2	102,5
Вариант 2	100,6	98,0	102,8	102,7	103,0
ВВП, млрд руб.
Вариант 1	71406.4	74905,2	82834,9	91091,2	99717,5
Вариант 2	71406.4	75716.5	83985.6	93239.8	103239.7

При построении среднесрочного прогноза ВВП России использовались прогнозы сценарных условий и основных макроэкономических параметров Министерства экономического развития Российской Федерации на 2016 г. и на плановый период 2017 и 2018 гг. в составе двух вариантов – вариант 1 (базовый сценарий) и вариант 2 (оптимистический сценарий) [8] .

Список литературы Агрегированная производственная функция с учетом научно-технического прогресса для экономики России

Андрианов Д.Л., Гребнев М.И. Обзор методов агрегирования производственных функций//Управление экономическими системами: электронный научный журнал. 2015. №1. URL: http://uecs.ru/uecs-73-732015/item/3307-2015-01-12-13-07-45 (дата обращения: 22.10.2015).
Бессонов В.А., Цухло С.В. Анализ динамики российской переходной экономики. М.: Институт экономики переходного периода, 2002. С. 589.
Гребнев М.И. Построение агрегированной производственной функции для экономики России//European Social Science Journal. 2013. №12 (Т. 1). С. 438-445.
Гребнев М.И., Андрианов Д.Л., Шульц Д.Н. Свидетельство о государственной регистрации программы для ЭВМ №2015619466. ПРОГНОЗ. Система балансировки стратегических прогнозов социально-экономического развития Российской Федерации, ее регионов и отраслей (ПРОГНОЗ. СБСП СЭР РФ). Заявка № 2015616036, дата поступления 30 июня 2015 г., дата государственной регистрации в Реестре программ для ЭВМ 04 сентября 2015 г.
Официальный сайт ЗАО «ПРОГНОЗ». URL: http://www.prognoz.ru/(дата обращения: 22.10.2015).
Перский Ю.К., Шульц Д.Н. Иерархический анализ экономики: методы и модели. Екатеринбург: Институт экономики УрО РАН, 2008. 225 с.
Поспелов И.Г., Поспелова И.И., Хохлов М.А., Шипулина Г.Е. Новые принципы и методы разработки макромоделей экономики и модель современной экономики России. М.: ВЦ РАН, 2006. 239 с.
Сценарные условия, основные параметры прогноза социально-экономического развития Российской Федерации и предельные уровни цен (тарифов) на услуги компаний инфраструктурного сектора на 2016 год и на плановый период 2017 и 2018 гг./Министерство экономического развития Российской Федерации. Москва, май, 2015. URL: http://economy. gov.ru/(дата обращения: 08.07.2015).
Felipe J., Fisher F.M. Aggregation in production functions: What Applied Economists should know//Metroeconomica. Vol. 54, №3. 2003. P. 208262.
Klein Lawrence R. Macroeconomics and the theory of rational behavior//Econometrica. 1946. Vol. 14, № 2. P. 93-108.
Klein Lawrence R. Remarks on the theory of aggregation//Econometrica. 1946. Vol. 14, № 4. P. 303-312.
May K. The aggregation problem for a one-industry model//Econometrica. 1946. Vol. 14, № 4. P. 285-298.
May K. Technological change and aggregation//Econometrica. 1947. Vol. 15, №1. P. 51-63.
Nataf A. Sur la Possibilite de Construction de certainsMacromodeles//Econometrica. 1950. Vol. 16. P. 232-244.
Shou Shan Pu. A Note on Macroeconomics//Econometrica. 1946. Vol. 14, №4. P. 299-302.

Еще

Статья научная