Ахроматизированные дифракционно-рефракционные объективы EUV-диапазона

Одной из явно выраженных тенденций современной инструментальной оптики является проникновение в коротковолновую часть электромагнитного спектра. Это, прежде всего, обусловлено стремлением за счёт уменьшения длины волны по высить разрешение оптической системы. Например, в оптической литографии начиная с 70-х годов прошлого века наблюдается последовательный переход от коротковолновой части видимого диапазона (436 нм, 70-е годы) к ближнему вакуумному ультафиолету (248 нм, 90-е годы), далее к глубокому ультрафиолету (193 нм и 157 нм, начало века) и, наконец, к экстремальному ультрафиолетовому (EUV) излучению в настоящее время и, по всей вероятности, в ближайшем будущем [1, 2].

В EUV-диапазоне, охватываю щем длины волн от 10 до 50 нм, сегодня исследуются и разрабатываются, в частности, нанолитографические оптические системы, ориентированные на длины волн (12 ,…, 14 нм), примыкающие к границе мягкого рентгеновского диапазона [3]. При этом исследуются и создаются системы на основе зеркал нормального падения. Системы на основе таких зеркал в отличие от систем с зеркалами скользящего падения, использовавши хся на первых этапах освоения излучения EUV- и рентгеновского диапазонов, имеют более низкий уровень полевых аберраций, что обеспечивает высокое разрешение в пределах полей изображения, которые в ряде случаев оказываются приемлемыми. Зеркала нормального падения этого диапазона многослойны [4]. Например, на длине волны λ=13,5 нм многослойное покрытие зеркала представляет собой чередую щиеся слои кремния и молибдена с толщинами 4,14 нм и 2,76 нм, соответственно. Покрытие из сорока пар таких слоёв обеспечивает коэффициент отражения не ниже 65% при углах падения излучения до 10° [5].

Ограничения, присущие всем зеркальным системам, и, прежде всего, центральное экранирование, а также сравнительно невысокий коэффициент отра- жения, ограничивающий количество используемых в системе зеркал и, в конечном счёте, размер полезного поля изображения, вынуждают искать альтернативные пути построения оптических систем. При этом традиционные рефракционно-линзовые системы приходится исключить, поскольку сегодня не существует материалов, имеющих приемлемое пропускание в диапазоне от 100 нм вплоть до жёсткого рентгеновского излучения. Даже в так называемых «окнах прозрачности» материалов излучение проникает в них на глубину не более десятка микрометров [6].

Проблематично использование и систем, со-стоящи х только из дифракционных оптических элементов, поскольку для обеспечения высокого разрешения они требуют квазимонохроматических источников излучения со спектральной полосой, не превышаю щей десятых, а то и сотых долей пикометра. Причём если в оптическом диапазоне проблема ахроматизации изображающих дифракционно-линзовых систем практически неразрешима (в силу того, что в этом диапазоне коэффициент дисперсии дифракционной линзы (ДЛ) существенно меньше коэффициента дисперсии любого оптического материала [7]), то в EUV- и рентгеновском диапазонах решение проблемы ахроматизации возможно благодаря специфике дисперсионных свойств материалов в этих диапазонах. Это решение предполагает введение в дифракционно-линзовую систему оптически слабой рефракционной линзы (РЛ). Причём снизить до приемлемого уровня по-гло щение излучения материалом РЛ можно, уменьшив его толщину в результате перехода к рефракционной линзе Френеля (РЛФ) [8-11].

Дисперсионная модель кремния

При длинах волн электромагнитного излучения короче 50 нм выражения для диэлектрической проницаемости г и показателя преломления вещества n записывают в виде [12]

г = 1 - 2 8+ i р (1) и n = 1 -8 . (2)

Здесь δ – оптическая константа вещества, называемая декрементом показателя преломления и отвечающая за рефракцию, β – оптическая константа ве щества, описываю щая его погло щательную способность и связанная с линейным коэффициентом поглощения µ , входящим в закон Бугера-Ламберта, соотношением [13]

β= ( λ I 2 π ) µ , (3) где λ – длина волны излучения.

Одним из наиболее пер спективных материало в для оптических элементов в EUV-диапазоне является кремний, у которого за L-краем погло щения в сторон у увеличения длин волн имеется област ь примерно от 12,4 до 15,4 нм, в пределах котор ой β практически постоянна и не п ревышает 0,002, что обеспечивает глубину проникновения более 0,5 мкм. Напомним, что под глубиной проникновения понимают глубину, на которой интенсивность излучения в ве ществе падает примерно на 64% от первоначального значения, т.е. уменьшается в e раз.

В табл. 1 представлены значения показателя преломления кремния для набора длин волн за L-краем поглощения от 12,42 до 12,58 нм. Эти значения приведены в [14] и получены на основе работы [15], опирающейся на исследования, проведённые в Центре рентгеновской оптики Берклеевской лаборатории им. Лоуренса (Lawrence Berkeley Lab, Ctr Xray Opt). Выбор длинноволновой границы обусловлен неуклонным приближением показателя преломления кремния к единице при дальнейшем увеличении длины волны.

Таблица 1. Показатель преломления кремния в диапазоне от 12,4175 до 12,580 нм

λ , нм	n	λ , нм	n	λ , нм	n
12,4175	1,013116	12,4575	1,010611	12,525	1,008802
12,4225	1,012619	12,4625	1,010343	12,535	1,008578
12,4275	1,012215	12,4675	1,010082	12,545	1,008353
12,4325	1,011943	12,475	1,009917	12,555	1,008127
12,4375	1,011677	12,485	1,009695	12,565	1,007901
12,4425	1,011411	12,495	1,009473	12,575	1,007674
12,4475	1,011145	12,505	1,009250	12,580	1,007561
12,4525	1,010877	12,515	1,009026

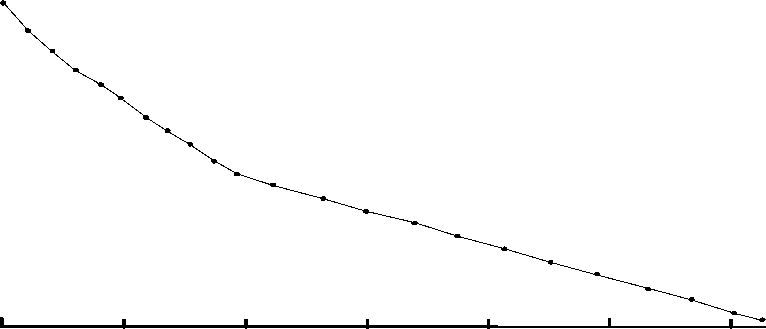
Аппроксимация данных табл. 1 ни одной из дисперсионных формул, общепринятых при описании оптических материалов, не даёт удовлетворительного результата. С другой стороны, если обратиться к рис. 1, на котором данные этой таблицы представлены графически, то видно, что в выделенном спектральном диапазоне имеются две области (назовем их условно «коротковолной» и «длинноволновой»). В «коротковолновой» области (от 12,4175 до 12,4675 нм) показатель преломления

1,012525

1,011816

1,011107

1,010397

1,009688

1,0089 79

1,0082 70

1,007561

12,45'5       12.4435       12,4695       12,4955       12,5215       12,5475       12,5735 x, им

Рис. 1. Графическое представление табличных значений показателя преломления кремния

Исследования, проведённые с использ ование м программы оптического проектирования «ZEMAX» [16], показа ли, что из набора, включаю ще го диспер сионные формулы Шотта, Герц-бергера, Конради и Зельмейера, наименьшее сред- относительно высок и достаточно сильно изменяется с длиной волны по ярко выраженному нелинейному закону. В «длинноволновой» области (от 12,4675 до 12,58 нм), наоборот, показатель преломления относительно мал (т.е. ненамного превышает единицу) и относительно слабо изменяется с длиной волны по закону, близкому к линейному. Поэтому представляется целесообразным для каждой из выделенных областей использовать свою дисперсионную формулу.

неквадратиче ское откл онение обеспечивает одна и та же дисперсионная формула Шотта с отличающимися коэффициентами для каждой из выделенных спектральных областей . Значения коэффициентов a0, …, a5 формулы Шотта n2 = a 0+a1%2 + a2% 2 + a3%-4 + a4% 6 + a5% 8 (4) для выделенных «коротковолновой» и «длинноволновой» областей представлены в табл. 2.

Благодаря использованию индивидуальных наборов коэффициентов a ₀ , …, a ₅ для каждой из выделенных спектральных областей удалось понизить среденеквадратическое отклонение показателя преломления, даваемого формулой Шотта, от табличных значений, доведя их для «коротковолновой» области до 6,7 10^-5 и для «длинноволновой» области до

1,4 10-7. Для визуализации достигнутого результата на рис. 2 представлены дисперсионные кривые, построенные по формуле Шотта для двух выделенных областей, и точки, соответствующие табличным значениям показателя преломления кремния. Плавность и монотонность этих кривых (с учётом приведённых значений среднеквадратических отклонений и практически достижимых на сегодняшний день точностей определения оптических констант материалов вблизи краёв поглощения) позволяет считать представленную аппроксимацию вполне приемлемой.

Таблица 2. Коэффициенты дисперсионной формулы Шотта для кремния

Спектральная область	Значения коэффициентов, соответствующие длине волны, измеренной в микрометрах
	a 0 х 10 5	a 1 х 10 5	a 2 х 106	a 3 х 10 7	a 4 х 1010	a 5 х 1014
« коротковолновая»	1,056509027	2,726280901	3,411640067	7,42296530	-2,5120554	1,28104688
« длинноволновая»	0,1760536166	0,4605080034	0,5608589056	1,90937156	-0,2278502	0,12577152

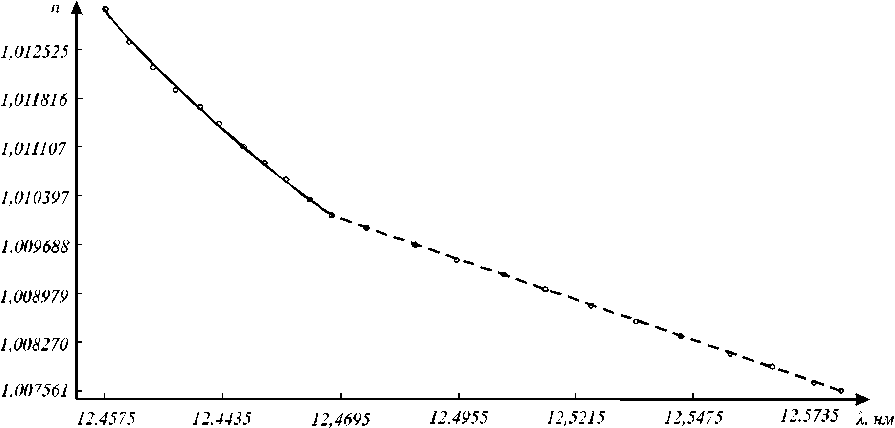
Рис.2. Дисперсионные кривые для двух выделенных спектральных областей и точки, соответствующие табличным значениям показателя преломления кремния

Компоновка и расчёт объективов

Компоновку, порядок расчёта и анализ возможностей ахроматизированных дифракционнорефракционных объективов EUV-диапазона продемонстрируем на примере конфокального объектива с телецентрическим ходом лучей, который может быть использован, в частности, в нанолитографии. Исходя из требования минимизации числа элементов в объективе, в силу их весьма невысокой энергетической эффективности в этой области спектра, в качестве исходной выберем схему объектива, состоящего из трёх ДЛ, одна из которых, размещённая в плоскости апертурной диафрагмы, имеет нулевую оптическую силу, т.е. является дифракционной асферикой [17, 18]. Кроме того, что этот объектив является конфокальным, в нём осуществляется пропорциональный (подобный) ход лучей, что обеспечивается расположением предмета и изображения в фокальных плоскостях передней и задней ДЛ, а промежуточное изображение в пространстве между этими ДЛ – в беско- нечности. Выбор данной исходной схемы обусловлен также и тем, что у этого объектива число одновременно устранимых аберраций многократно превышает число коррекционных параметров. В результате он может быть свободным от всех монохроматических аберраций третьего и пятого порядков, за исключением второй комы пятого порядка. При этом сферическая аберрация и дисторсия отсутствуют во всех порядках аберрационного разложения. В результате апертура объектива не ограничивается аберрациями и разрешение, по крайней мере, на оптической оси, может быть соизмеримо с длиной волной. При этом благодаря отсутствию дисторсии изображение, формируемое объективом, остаётся ортоскопическим.

Габарит системы L , т.е. расстояние от плоскости предмета до плоскости изображения, линейное увеличение M и числовую апертур у в пространстве изображений А' выберем, исходя из требований, предъявляемых к литографическим объективам в EUV-области спектра, а также с учётом сегодняш- них возможностей изготовления ДЛ. Как показано в [19], ДЛ сравнительно большого диаметра (до D =10 мм) могут изготавливаться с числом зон до 50000 и минимальной шириной зоны до bmin =30 нм. Поэтому увеличение и числовая апертура были приняты равными M =-0,25 и Α′ =0,2, а в качестве предельного значения габарита было принято L =150 мм. Этим параметрам соответствуют следую щие значения конструктивных параметров длиннофокусной (обращённой к плоскости предмета) и короткофокусной (обращённой к плоскости изображения) ДЛ объектива. Для длиннофокусной ДЛ D =10 мм и bmin =75 нм, для короткофокусной ДЛ D =7 мм и bmin =30 нм.

Оптимизация выбранной исходной схемы при фиксированных значениях L , M и Α′ привела к небольшом у изменению всех конструктивных параметров объектива: переднего и заднего отрезков, расстояний между ДЛ и значений коэффициентов, определяющи х вид зависимостей пространственных частот микроструктур ДЛ. В результате при использовании монохроматического излучения объектив оказался способным формировать высококачественное изображение по полю 2 y ′ =1,2 мм. Практическое совпадение качества изображения с дифракционно-ограниченным гарантируется тем, что в пределах всего указанного поля нормированная интенсивность в дифракционном фокусе, т.е. интенсивность Штреля I _S ≥ 0,999, а среднеквадратическая величина волновой аберрации не превышает 0,004λ. Сразу же отметим, что эти результаты могут быть получены при оптимизации на любой длине волны из выбранного выше спектрального диапазона, т. е. от 12,42 нм до 12,58 нм.

Ширина спектрального диапазона этого чисто дифракционного объектива, оценённая по весьма мягкому для фотолитографических объективов критерию Марешаля ( I _S ≥ 0,8) [20], составляет всего ∆ λ = ± 0,13 пм. Расширить спектральный диапазон удалось путём ахроматизации, выполненной за счёт замены относительно оптически слабой ДЛ, расположенной в плоскости апертурной диафрагмы на рефракционно-дифракционный корректор (ДРК), имеющий ту же оптическую сил у, что и заменяемая ДЛ и включающий помимо ДЛ кремниевую РЛ.

Напомним, что ахроматизация предполагает устранение хроматизма положения для крайних длин волн выбранного спектрального диапазона, т.е. достижение равенства задних отрезков на этих длинах волн ( s _λ′ _min = s _λ′ _max ). Эффективность же ахроматиза-ции оценивается по вторичному спектру, т.е. по максимальной разнице значений заднего отрезка объектива в пределах спектрального диапазона ах-роматизации. Обычно за величину вторичного спектра принимают

∆s′ = s′ - s′ , (5)

λ λmax где sλ′ - задний отрезок оптической системы на центральной длине волны λ этого диапазона.

Поскольку рассматриваемый объектив является конфокальным, а ДРК, размещённый в плоскости его апертурной диафрамы практически афокален, то высоты падения апертурного параксиального луча на все элементы объектива можно считать одинаковыми. В этом случае условие ахроматизма сводится к уравнению [21]

^{φ R} + ¹ ∑ ^J φ D j = 0 , ν Si ν D j = 1

откуда требуемая для ахроматизации величина оптической силы РЛ определяется выражением

φ R =-^{ν Si} ∑ ^J φ D j .                               (7)

ν D j = 1

Что же касается величины вторичного спектра, то при выполненном условии ахроматизма он может быть оценён по формуле

∆ s ′= s λ ′ ²( ^{γ D -γ Si}) ∑ ^J φ D j .                        (8)

ν D      j = 1

В формула х (6)-(8) φ _R и φ _{D j} - оптические силы РЛ и ДЛ объектива на длине волны λ ; ν _Si , γ _Si и ν _D , γ _D - коэффициенты дисперсии и относительные частные дисперсии кремния и ДЛ, соответственно. Последние рассчитываются с помощью уравнений

νSi =(nλ-1)I(nλmin - nλmin ),(9)

γSi=(nλmin-nλ)/(nλmin-nλmax),(10)

νD =λ/(λmin -λmax),(11)

γD =(λmin-λ)/(λmin-λmax).(12)

Учитывая предполагаемую замену в дифракционно-рефракционном конфокальном объективе РЛ на РЛФ (см. рис. 3), при расчётах РЛ полагалась тонкой плоско-выпу к лой линзой. Её оптическая сила на длине волны λ связана с радиусом кривизны выпуклой поверхности r соотношением

φ _R = - ( n _λ - 1)/ r = δ_λ / r .                        (13)

Оптические характеристики кремния n _λ , δ _λ , ν _Si и γ Si в «коротковолновой» и «длинноволновой» областях спектра существенно отличаются. В табл. 3 представлены оптические и сопоставительные характеристики кремния и ДЛ, вычисленные для середины каждой из указанных областей в пределах достаточно узких спектральных участков одинаковой ширины ( ∆ λ = ± 5 пм). Из результатов расчётов, выполненных по формулам (7) и (13) с учётом данных табл. 3, следует, что ахроматизация в «коротковолновой» области достигается при радиусе кривизны вып уклой поверхности кремниевой линзы примерно в три раза большем, чем в «длинноволновой»

области. Это обусловлено тем, что для этих областей отношения νD I νSi , определяю щие оптическую силу кремниевой линзы, отличаются примерно в два раза, а δλ - примерно в полтора раза.

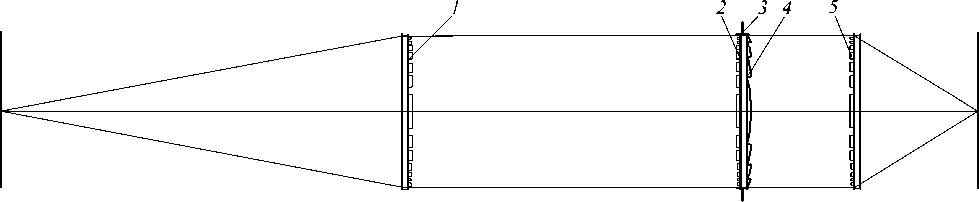
Рис.3. Оптическая схема дифракционно-рефракционного конфокального объектива:

1, 2, 5 – ДЛ, 3 - апертурная диафрагма, 4 - РЛФ

Таблица 3. Оптические и сопоставительные характеристики кремния и ДЛ

Спектральная область	λ , нм	n	δ λ	ν DL / ν Si	1 γ Si -γ DL
«коротковолновая»	12,435	1,011842	-0,011534	64,6	0,0145
	12,440	1,011534
	12,445	1,011243
«длинноволновая»	12,525	1,008802	-0,008690	32,4	0,0003
	12,530	1,008690
	12,535	1,008578

Что же касается величины вторичного спектра, то она в «коротковолновой» области примерно на два порядка больше, чем в «длинноволновой» области. Это обстоятельство, а также то, что большая кривизна преломляющей поверхности, как правило, приводит к значительному уровню полевых монохроматических аберраций, даёт все основания предполагать, что объектив, рассчитанный на «коротковолновую» спектральную область, будет формировать высококачественное изображение большего диаметра, но в более узком спектральном интервале.

Действительно, объектив, работающий с увеличением M =-0,25 и рассчитанный на квазимонохрома-тическое излучение с шириной линии ∆ λ = ± 5 пм в «коротковолновой» области спектра ( λ =12,42 нм) при числовой апертуре в пространстве изображений Α′ =0,2 и габарите L =115 мм, обеспечивает высококачественное плоское изображение диаметром 2y′ =1 мм. Объектив, работающий с тем же увеличением, но рассчитанный на полихроматическое излучение с шириной полосы ∆ λ = ± 50 пм в «длинноволновой» области спектра ( λ =12,527 нм), при числовой апертуре в пространстве изображений Α′ =0,2 и габарите L =123 мм обеспечивает высококачественное изображение диаметром 2y′=0,125 мм. Изображения, формируемые обоими объективами, орто-скопичны (дисторсия по всему полю изображения не превышает 6 пм) и практически не отличаются от дифракционно-ограниченного в пределах приведённых полей, поскольку среднеквадратическая величина волновой аберрации не превышает 0,054λ , а интенсивность Штреля IS ≥ 0,9. При регистрации изображения, формируемого этими объективами, EUV- резистом [4], благодаря низкому уровню остаточных аберраций разрешение будет превышать релеевское и составлять величину порядка 34 нм.

Заключение

Световые диаметры и минимальные размеры элементов квазипериодических микроструктур ДЛ рассчитанных дифракционно-рефракционных объективов соответствуют сегодняшним возможностям их изготовления и не превышают приведённые выше значения для ДЛ чисто дифракционного объектива. Что же касается ДРК, то он может быть выполнен в виде единого элемента, на одной стороне которого микроструктура ДЛ, а на другой – РЛФ. Толщина такого элемента составляет несколько десятых долей микрометра, а жёсткость конструкции обеспечивается, например, радиальными спицами. В настоящее время предложено несколько вариантов подобных конструкций. Одна из них описана в работе [22].

Результаты, представленные в данной статье, позволяют сделать вывод о том, что ахроматизированные дифракционно-рефракционные объективы по совокупности характеристик, включающих размер плоского поля высококачественного изображения при на порядок меньшем габарите, технологически реализуемые световые диаметры и минимальные размеры элементов квазипериодических микроструктур являются конкурентоспособными по отношению к зеркальным объективам, которые ещё совсем недавно в EUV-диапазоне считались безальтернативными.

Работа выполнена при поддержке Министерства образования и науки РФ в рамках федеральной целевой программы «На учные и научно-педагогичес- кие кадры инновационной России» на 2009–2013 годы (Госконтракт 16.740.11.0145).