Аэродинамика самолёта в возмущённой атмосфере

Для моделирования вихревого следа, за. самолётом со стреловидным крылом типа. Су-27 [1] решается краевая задача, для осреднённых по Рейнольдсу уравнений Навье-Стокса. Из полученного поля скоростей извлекается начальная вихревая структура, эволюция и стохастика которой моделируются дискретными вихрями с ядром вихря Рэнкина. Учёт затухания циркуляции производится на. основании экспериментальных данных и расчётов в рамках прямого численного моделирования больших вихрей (LES) [2-3]. Для вычисления приращения сил и моментов, возникающих на. последующем самолёте написана, компьютерная программа, на. базе панельного метода. [4].

Вихревые структуры за. тонкими стреловидными крыльями с наплывом малого удлинения имеют особенности по сравнению с вихревым следом за. самолётом с крылом большого удлинения малой стреловидности с профилями большой относительной толщины. Когерентные структуры за. крыльями истребителей формируются быстрее, они более подвижны из-за. малого размаха, вихрей и возможного взрыва, вихря [5], возникающего при больших углах атаки, с последующим его восстановлением.

Для верификации сеточных методов расчета стационарных течений в работе [6] предложены два критерия, основанные на принципе максимума давления [7], согласно которому поверхности Q = 0.5(РуРу — StjStj ) = 0 разделяют область течения на подобласти, где Q >  0, в которых не может быть локального максимума давления, и Q < 0, где не может быть локального минимума. Здесь ^tj = 0.5(уу¹ — уу^) - тензор завихренности, Stj = 0.5(ду¹ + ^у²") ~ симметричный тензор скоростей деформации.

Так как в ядре вихря имеется разрежение и область отрыва характеризуется пониженным давлением, то Q < 0 в этих областях свидетельствует о нарушении принципа максимума давления. На основании этого в [6, 8] предложены критерии, требующие положительности Q в ядрах вихрей и областях отрыва потока. С целью верификации полученных результатов следует проверять, чтобы внутри вихревых и отрывных зон выполнялось условие Q >  0. В данной работе эти критерии применены для оценки качества расчёта (достаточности размеров расчётной области, густоты сетки, числа итераций) конкретной реализации метода на имеющейся вычислительной технике.

2.    Постановка задачи

Решается краевая задача (КЗ) для осреднённых по Рейнольдсу уравнений Навье-Стокса (RANS) с двухпараметрической к — ш SST моделью замыкания. Рассматривается горизонтальный полёт самолёта типа Су-27 [1] со скоростью 280 м/с под углом атаки 4°, без скольжения. Расчёт выполнен для половины пространства с продольной вертикальной плоскостью симметрии. Параметры атмосферы: температура воздуха 300 К, атмосферное давление 101 325 Па, плотность воздуха 1.225 кг/м3. Расчёт ведётся при среднем уровне турбулентности с шагом по времени: dt = 0.0005 с.

Вид расчётной области и поверхности самолёта показан на рис. 1.

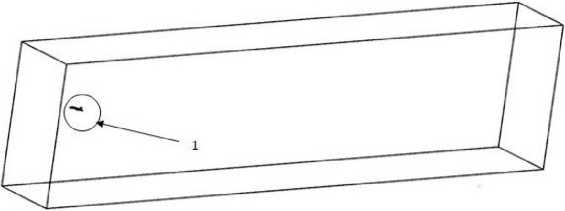
Рис. 1. Вид расчётной области и самолёта. (1)

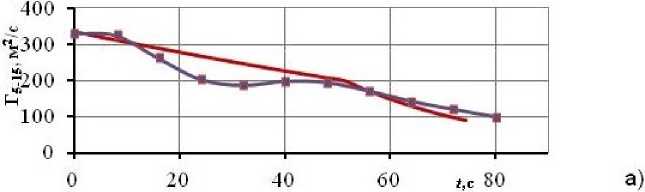
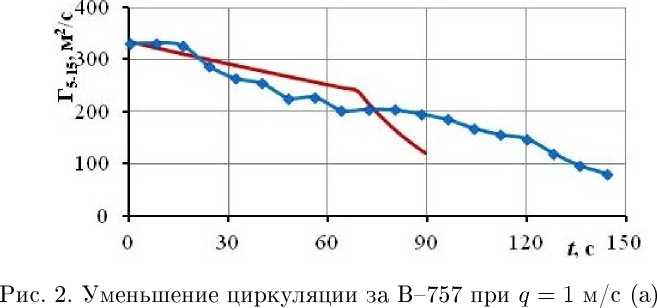
Расчёт выполнен на. сетке, имеющей 10 021 942 узлов, с помощью программного пакета. ANSYS FLUENT (лицензия МФТИ № 1079611). На выходной границе расчётной области формируется когерентная вихревая структура, динамика и стохастика которой в области дальнего следа, моделируется дискретными вихрями, начальное положение ядер которых и величина, циркуляции определяются из решения краевой задачи для RANS. В ходе методических расчётов получена, инженерная оценка, скорости спадания циркуляции при разных уровнях атмосферной турбулентности [2-3]. На рис. 2 приведены результаты уменьшения циркуляции вихря за. самолётом В-757 по времени при двух уровнях атмосферной турбулентности. Вихревой след за. самолётом В-757 отличается очень плотным ядром с максимальной тангенциальной скоростью на. границе ядра, порядка. 100 м/с. На рисунках наряду с результатами расчёта, методом прямого численного моделирования крупных вихрей (LES), помеченных маркерами, приведены данные по инженерной модели ЦАГИ [9].

3.    Результаты численного моделирования

Распределение давления и температуры на. поверхности самолета, приведено на. рис. 3-4.

б)

и 0.5 (б)

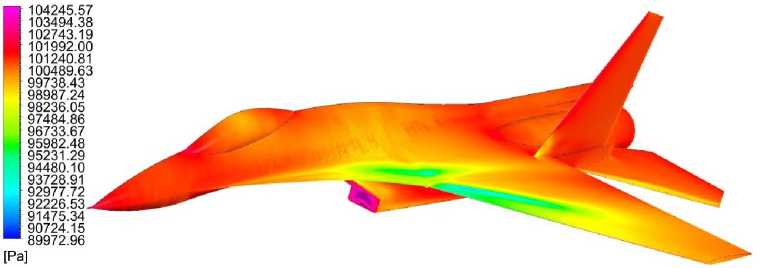
Рис. 3. Распределение давления по поверхности самолёта

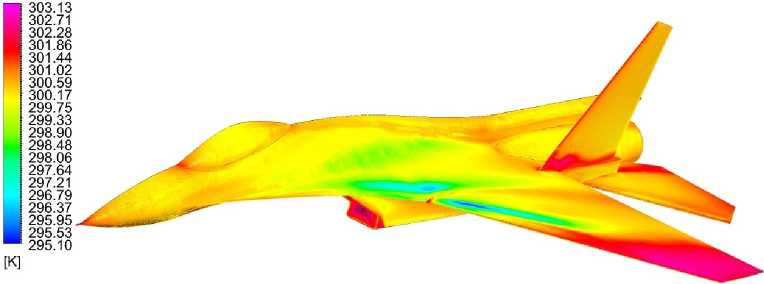
Рис. 4. Распределение температуры по поверхности самолёта

Результаты расчёта, представленные в виде поверхности Q = 0 (рис. 5) и поля Q = соnst > 0 (рис. 6), демонстрируют положительность инварианта Q в ядрах вихрей, что может служить подтверждением высокого качества полученного решения.

Рис. 5. Поверхности Q = 0 при расчёте обтекания самолёта

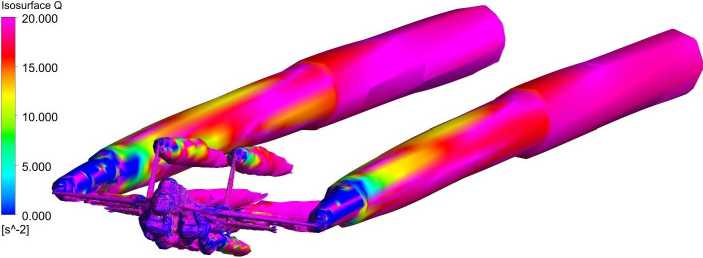
Рис. 6. Поле 0  20

На рис. 7 приведены поля продольной компоненты завихренности в поперечных сечениях следа ж = 0.5 и ж = 6. В сечении ж = 0.5 вихревая структура сформировалась в виде двух пар вихрей. Это начальное поле выбрано для последующего моделирования.

Динамика и стохастика следа моделируются в компьютерном коде COSMA (Coherent vortex Structure of Mounting Airport). На рис. 8 приведены начальные поля компонент скорости v и w в сечении ж = 0.5.

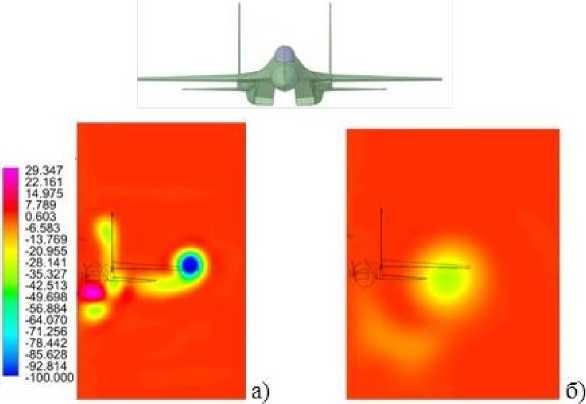
Рис. 7. Поле продольной компоненты завихренности в сечении ж = 0.5 (а), ж = 6 (б) при виде спереди

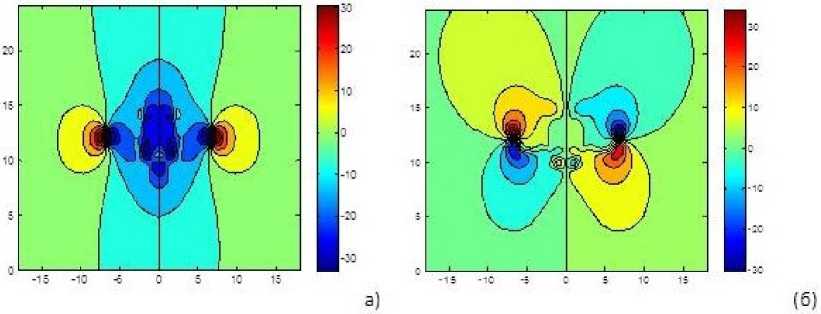
Рис. 8. Поля v (а)

и w (б) в сечении ж = 0.5

С помощью численного дифференцирования находятся производные компонент скорости v и w по у и д (рис. 9) и формируется продольная компонента вектора завихренности ш(ж) (рис. 10). Определяется положение максимумов в поле завихренности, вычисляется циркуляция в окрестности экстремумов в пределах заданных радиусов вихрей и полная циркуляция вихрей.

Задается фоновый уровень циркуляции, ниже которого вихри не рассматриваются, формируется когерентная структура следа (рис. 11). Наблюдаются один сильный вихрь у = 12.05 а I. д = 6.75 м, Гі = -247 м²/с.

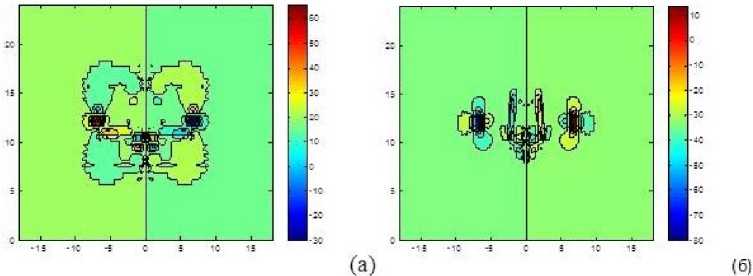
Рис. 9. Производные ^^ (^а) и |^ (б) в сечеиии х = 0.5

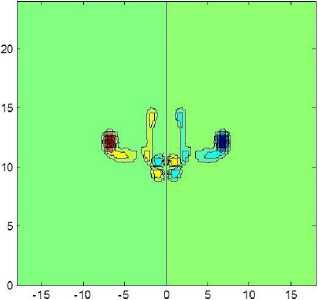
Рис. 10. Поле продольной компоненты завихренности в сечении х = 0.5

-20

-40

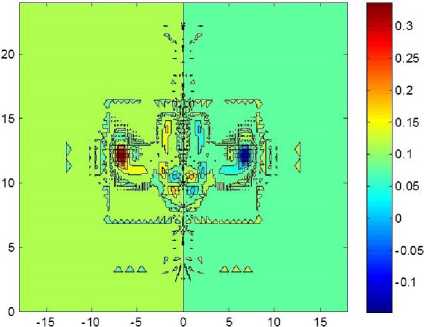
Рис. 11. Когерентная структура следа в сечении х = 0.5

Для моделирования вихревого следа использованы вихри с профилем скорости вихря

Рэнкина (рис. 12):

V (р) =

Г (^0/2) • р, р <  а,

((шо • а²/2)/р,    р >  а.

В качестве совершающего полёт в условиях роторной турбулентности самолёта рассматривается двухдвигательный легкий транспортный самолет с повышенным уровнем несущих свойств крыла. Аэродинамическая компоновка (рис. 13) выполнена по схеме «высокоплан» с «палубным» расположением хвостового оперения [10]. Рассматривается ситуация, когда атмосферная турбулентность мала, а пилот последующего самолёта, вопреки существующим правилам (или ввиду малости видимого размера предшествующего самолёта), не выдерживает безопасной дистанции между самолётами.

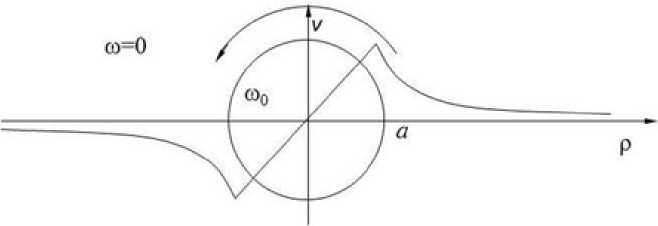
Рис. 12. Профиль скорости в вихре Рэнкина.

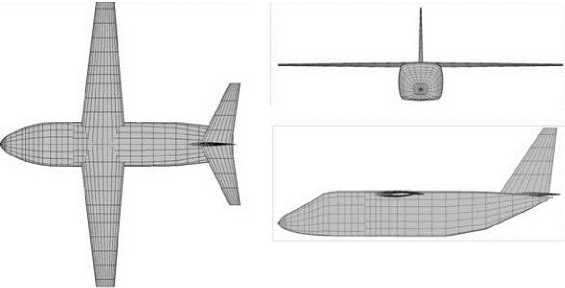
Рис. 13. Самолёт «Битюг»

В табл. 1 приведены результаты расчёта, когда, плоскость симметрии последующего самолёта. параллельна, плоскости симметрии генератора, следа. В первом примере они совпадают Дг = 0 (рис. 14а), а положение носовой оконечности фюзеляжа находится на уровне вихрей, или в плоскости, проходящей через центр одного из вихрей (рис. 14 б-в).

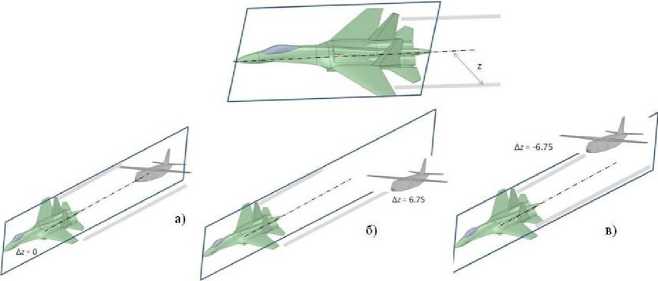
Рис. 14. Схема, расположения самолётов при численном моделировании

Максимальные величины индуцированного момента крена при Дг = +/ — 6.75, у = 12.05, Дт_х = +/ — 0.1195 превышают располагаемые управляющие значения при отклонении элеронов на максимальные углы (|Дт_жэл._расп| = 0.055). Располагаемое значение момента рыскания при отклонении руля направления на угол 25° (|Дт_урн. _расп 1 = 0-045) примерно в 3 раза, превышает максимальную индуцированную величину путевого момента. Дт-_д = —/ + 0.0127 пр и Дг = +/ — 6.75, у = 0.

Для валидации полученных результатов использованы экспенриментальные данные, полученные в АДТ Т-103. Модель изготовлена, в масштабе 1:6.5 по отношению к натурному самолету. Её основные геометрические параметры даны в таблице 2. Бортовое сечение крыла, установлено под нулевым углом относительно строительной горизонтали фюзеляжа.

Испытания модели самолета проведены при скорости потока V = 50 м/с (М ~ 0.15), соответствующей числу Re ~ 1 х 106, по средней аэродинамической хорде крыла. При вычислении коэффициентов аэродинамических сил и моментов в качестве характерных размеров приняты площадь, средняя аэродинамическая хорда и размах крыла модели.

Т а б л и ц а 1

Результаты расчёта приращений сил и моментов, действующих на самолёт, под действием спутной турбулентности

△ z = 0
У	△ с	△ Су	△ с	△ тж	△ ту	△ т^
0	-0.0186	0.7878	-0.0005	0.00003	-0.00005	-0.1431
12.05	-0.0344	1.4907	0.00005	0.0001	0.00002	-0.2466
△ z = 6.75
0	-0.0151	0.6244	-0.0430	0.0322	-0.0128	-0.1131
12.05	-0.0204	0.8446	0.0170	0.1195	0.0047	-0.1529
△ z = -6.75
0	-0.0150	0.6262	0.0425	-0.0321	0.0127	-0.1149
12.05	-0.0202	0.8339	-0.0170	-0.1195	-0.0047	-0.1480

Таблица2

Основные геометрические параметры модели

Площадь крыла, м2	0.71
Размах крыла, м	2.49
Относительное удлинение	8.76
Сужение крыла	2.56
Средняя аэродинамическая хорда, м	0.303
Относительная площадь миделя фюзеляжа	0.161

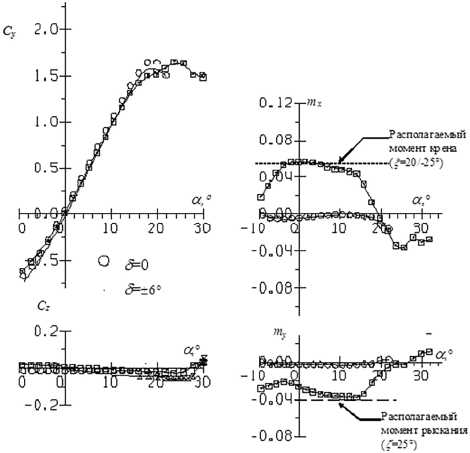
Рис. 15. АДХ модели в крейсерской конфигурации

На рис. 15 приведены аэродинамические характеристики (АДХ) модели в завихренном потоке. Интенсивность завихренности регулировалась изменением угла установки секций крыла имитатора скосов потока (5 = ±6°). Для сравнения даны аналогичные характеристики в равномерном потоке. Видно, что модель в завихренном потоке испытывает су- щественные изменения в величинах и поведении моментов крена mxa, и рыскания mga а также коэффициента подъёмной силы Сда.

Приведенные экспериментальные результаты удовлетворительно согласуются с результатами расчёта.

4.    Выводы

В качестве генератора когерентных вихревых структур может быть рассмотрен горный ландшафт, архитектурные сооружения (путепроводы, мосты), надстройки авианесущих кораблей и т.д.

Созданный метод может быть использован для поиска аэродинамических средств повышения уровня безопасности полета на режимах взлёта и посадки в условиях орографической турбулентности, а также выработки мер по повышению боевых возможностей фронтовой авиации при выполнении полётов в горной местности.