Актуаторная функция мышцы: модель генерации силы при изометрическом возбуждении

Ранее авторами [3] была разработана методика описания механического поведения мышечного моноволокна при реализации сократительной функции. Использование гипотезы «скользящих нитей» [1] и соотношений теории упругости позволяет определить распределение напряжений и деформаций по моноволокну при изотоническом и изометрическом возбуждении. Для этого составляется и решается система нелинейных дифференциальных уравнений в частных производных. Прямое и непосредственное использование данной методики при переходе от моноволокна к мышце представляется достаточно трудоемкой задачей. Поэтому при описании механического поведения мышцы приходится использовать ряд упрощений. Целью настоящей работы является адекватное описание деформирования всей скелетной мышцы на основе упрощенной модели мышечного моноволокна.

Упрощенная модель мышечного моноволокна

Известно [7], что моноволокна в скелетной мышце непрямолинейны. Данное обстоятельство обусловливает практически нулевую жесткость мышцы на сжатие и растяжение при малых деформациях. При этом градиенты напряжений в активном состоянии прямолинейного моноволокна для мышцы в целом будут пренебрежимо

малы. Данное обстоятельство позволяет считать распределение напряжений и деформаций в мышце однородным по длине и исследовать только временные зависимости параметров напряженно-деформированного состояния.

Нулевая жесткость на сжатие мышцы, находящейся в пассивном состоянии, позволяет при описании реализации сократительной функции учитывать только актиномиозиновое взаимодействие между нитями саркомера [6]. Данное взаимодействие описывается на основе гипотезы «скользящих нитей», которую можно сформулировать в виде двух дифференциальных уравнений nd         nd

n = k (α-n-m)+ ε; m = - ε-k m.

¹               2 δ             2 δ ²

Здесь n , m – количество «тянущих» и «тормозящих» поперечных актиномиозиновых мостиков, соответственно; k 1 , k 2 – временные константы образования и разрыва мостика, соответственно; α – общее число мостиков на половине длины саркомера; δ – расстояние между положениями равновесия тянущего и тормозящего мостика; d ≈ 2,2 мкм – длина саркомера; ε – продольная деформация мышечного моноволокна. Для адекватного описания функционирования мышечной ткани необходимо учитывать зависимость общего числа актиномиозиновых мостиков α от текущей длины саркомера при деформировании. Данная зависимость имеет сложный вид [10]. Не нарушая общности дальнейших выкладок, будем использовать следующую аппроксимацию данной зависимости

α ( ε ) =α _max(1 - 4 ε ²).

Актиномиозиновое взаимодействие создает в моноволокне осевое напряжение f

σ = S (n - m) . Здесь S – площадь поперечного сечения мышечного моноволокна; f – сила, генерируемая одним поперечным мостиком. Так как относительное скольжение нитей саркомера сопровождается перемещением массы, то при описании сократительной активности необходимо учитывать инерционные силы. Для осевого напряжения можно записать

f

σ = S (n - m) + kε .

Здесь k – коэффициент, характеризующий инерционность подвижных элементов саркомера. Значение k определяется экспериментально. Но приближенную оценку коэффициента k можно получить, зная длину моноволокна L и его плотность ρ . Для этого определим осевое напряжение σ ин , обусловленное только инертностью нитей саркомера:

ин _S ин

= mu . S^C

Здесь m = р SL - масса моноволокна; UC - ускорение центра масс. Используя допущение об однородном распределении деформации и напряжения по длине моноволокна, для ускорения центра масс можно записать:

uC

L =ε .

Подставив выражения для массы и ускорения центра масс, получим приближенную оценку коэффициента k .

k = ¹ L ² ρ .

Используя формулы (1) и (2), для описания процесса сокращения мышечного моноволокна составим два дифференциальных уравнения

— ( о- к e) = k a ( e ) - n (2 k_x - k ₂) + ^— ( о- k e ) (k_x - k ₂) + nd- e ;

f                                     f δ

n = к 1

S

a ( e ) - 2 n + у ( о- k e )

nd .

+    ε.

2δ

При решении системы (4) следует учитывать, что входящее в него напряжение σ обусловлено только актиномиозиновым взаимодействием. До активизации сократительной функции оно равно нулю. Если на моноволокно действует внешняя нагрузка, то процесс сокращения начнется только в тот момент, когда напряжение σ уравновесит эту нагрузку.

Сопоставим результаты использования системы (4) с данными, полученными на основе более сложной модели моноволокна. Подробная модель деформирования мышечной ткани, разработанная в [3], позволяет учесть сопротивление моноволокна на сжатие и описать неоднородное распределение деформаций и напряжений по длине. В соответствии с данной моделью при описании процесса активизации сократительной функции мышечного моноволокна составляется и решается система четырех дифференциальных уравнений в частных производных dd n = k (α-n-m)+n   u , m = -k m-n u ,

¹                   2 δ ^{,            2}       2 δ ^,

σ′ u=   ,

ρ

1    Hf

0 = — о + EU. + u +—

τ          τS

^{d     1}

k ₁ ( α - n - m ) + k ₂ m + n u + ( n - m ) .

5    т

В системе (5) E – мгновенный модуль упругости материала моноволокна; H – длительный модуль упругости; τ – время релаксации. Штрихами при перемещении и напряжении обозначена производная по координате x , отсчитываемой вдоль длины моноволокна. Математическую модель (5) в дальнейшем будем называть моделью вязкоупругого стержня».

В качестве примера использования систем (4) и (5) рассмотрим свободное изотоническое сокращение моноволокна при следующих значениях параметров: длина L = 0,07 м; площадь поперечного сечения S = 5 ⋅ 10 ^–9 м²; условная плотность материала ρ = 1000 кг / м³; время релаксации τ = 1 мс. Параметры актиномиозинового взаимодействия примем следующими: k 1 = 160 с^–1; k 2 = 88,9 с^–1; δ = 8 ⋅ 10^–9 м; f = 3 ⋅ 10^–12 Н; α max = 2 ⋅ 10⁶. Данные значения параметров, как было показано в работе [4], соответствуют портняжной мышце лягушки при температуре 0°С.

На рис. 1 представлены временные зависимости скорости свободного сокращения, рассчитанные на основе модели работы [3] и упрощенной системы (4). Видно, что через некоторый промежуток времени t уст ≈ 50 мс после начала активации мышечного моноволокна свободное сокращение является стационарным, т.е. при t >  t уст скорость сокращения изменяется со временем незначительно. При этом расчетные оценки значения t уст , полученные на основе точной (5) и упрощенной (4) моделей, практически совпадают.

v , см/с

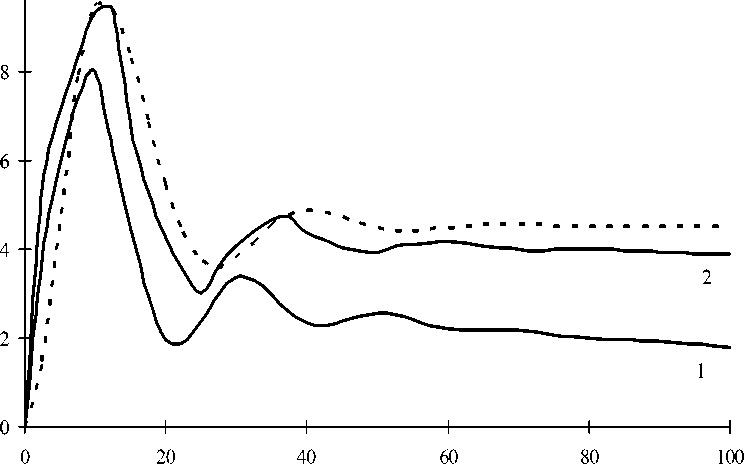
Временная зависимость скорости свободного сокращения. Сплошные кривые -

t , мс

Рис. 1.

использование математической модели (5); пунктирная - использование упрощенной модели (4). Кривая 1 построена для E = 10⁵ Па, H = 10⁴ Па; кривая 2 - E = 10⁴ Па, H = 10³ Па

Следует отметить, что при использовании подробной модели (5) скорость сжатия моноволокна для t >  t _уст несколько уменьшается со временем. Нарушение стационарности обусловлено жесткостью прямолинейного моноволокна на сжатие. В соответствии с моделью (5) характер зависимости v ( t ) скорости при t >  t _уст определяется вязкоупругими характеристиками ( E , H , т ) материала моноволокна. При использовании предложенной упрощенной модели (4) стационарность свободного сокращения не нарушается. В соответствии с системой (4) скорость свободного сокращения моноволокна в стационарном режиме определяется следующим образом:

v уст = ^{- L} ek, = ^{2 8 k} 2 L .

^J               t > t уст               d

Если сокращение моноволокна осуществляется при наличии ненулевого постоянного напряжения о ₀, то установившаяся скорость определяется по формуле

уст

2 3 Lk 1 k ₂( f a- S о ₀)

d ( к 1 + k ₂) ( S о ₀ + f a k 1 /( k 1 + k ₂) )

Введя обозначения:

flk, ,    28 Lk,k, „    , „ „

a = ——L, b =-----L^-, P = fa, P = Sо0, k 1+k 2      d (k 1 + k 2) 0               0

выражение (6) можно переписать в форме, аналогичной уравнению Хилла [8].

v = bP

- P

.

P + a

Известные экспериментальные данные [8, 9] о механическом поведении мышц свидетельствуют о неизменности скорости свободного изотонического сокращения в стационарном режиме вплоть до прекращения процесса активации. Значение скорости изотонического сокращения определяется по уравнению Хилла и зависит только от параметров актиномиозинового взаимодействия. Таким образом, предложенная упрощенная методика (4), являясь менее подробной по сравнению с моделью (4), позволяет, однако, более адекватно отразить известные особенности деформирования мышечной ткани. Важным преимуществом системы (4) является относительная простота расчетов, что существенно упрощает переход от отдельного моноволокна к скелетной мышце в целом.

Описание активного состояния мышцы

При переходе от отдельного мышечного моноволокна к мышце необходимо учитывать сложный характер взаимного расположения и ориентации волокон. Для описания структуры скелетной мышцы используем функцию L ( r ), которая определяет зависимость длины моноволокна L от расстояния до оси симметрии мышцы. При рассмотрении мышцы как крученой нити [5] длиной L 0 , радиусом R и углом крутки 0 функция L ( r ) будет иметь вид:

L ( r ) = L о

^{1 + tg} 2 ( R )

Если перед активацией сократительной функции мышце длиной L 0 было придано удлинение u , то функция L ( r ) позволяет определить начальную продольную деформацию каждого моноволокна

El

t = 0

77т ⁽ u ⁺ L о ^- L ⁽ r )), L ⁽ r ) <  L о ⁺ u ; <  L ⁽ r )

О, L (r ) >  L 0 + u.

При описании сокращения первоначально растянутой мышцы все моноволокна можно подразделить на две группы: 1) моноволокна, длина которых совпадает с заданной длиной мышцы L 0 + u ; 2) моноволокна, длина которые превышает длину мышцы. Волокна, относящиеся к первой группе, находится в изометрических условиях. При описании сократительной активности этих волокон в системе (4) следует положить:

^{E ( t} ) = ^EI t = 0

-1- ( u + L 0 - L ( r ) ), E ( t ) = i :( t ) = E( t ) = 0, „ I L ( r )

t = 0

= " t = 0 = ⁰.

В этом случае система (3) позволяет определить две функции времени: „ ( t ), а ( t ). При описании процесса генерации напряжения в изометрических условиях система (4) может быть решена аналитически

а ( t ) = ^и ( t ) = а S + Ce "  * 1 ^t .

Здесь C – константа, определяемая из начального условия.

Моноволокна второй группы находятся в условиях свободного сокращения:

^{с ( t} ) = ⁰, " I t = 0 = ^EI t = 0 = ^EI t = 0 =i i| t = 0 = °.

Для этих моноволокон система (4) позволяет вычислить n ( t ) и е ( t ). В ходе свободного сокращения длина моноволокна уменьшается. Как только величина L ( r ) [ 1 + е ( t ) ] сравняется с длиной мышцы L 0 + u , моноволокно, первоначально относящееся ко второй группе, перейдет в первую.

Численная реализация методики позволяет при заданном удлинении u определить временную зависимость осевого напряжения о во всех моноволокнах мышцы. Проинтегрировав напряжение о по площади поперечного сечения мышцы, вычислим общую сжимающую силу P , которая генерируется мышцей при активации сократительной функции.

Если длина мышцы L 0 + u поддерживается постоянной, сила P , обусловленная актиномиозиновым взаимодействием, возрастает от нуля до максимально возможного при данном удлинении u значения P max и в дальнейшем остается неизменной до завершения процесса активации. Данный режим функционирования мышцы называют изометрическим возбуждением [3]. Если поддерживается постоянной внешняя растягивающая сила Q , вызвавшая удлинение мышцы в пассивном состоянии, то генерируемая мышцей сила P перестанет изменяться, достигнув значения Q . С этого момента начнется уменьшение общей длины мышцы. Данный процесс называют изотоническим сокращением.

Пример расчета

В качестве примера использования разработанной методики рассмотрим изометрическое возбуждение мышцы, моделируемой крученой нитью длины L 0 = 0,1 м и радиусом R = 1 см. Площадь поперечного сечения и параметры актиномиозинового взаимодействия моноволокон, образующих данную мышцу, те же, что и для ранее рассмотренного моноволокна (см. рис. 1). Моделируемую мышцу удлиним на u и активируем сократительную функцию в изометрических условиях.

На рис. 2 представлены расчетные временные зависимости силы P , генерируемой мышцей в рассматриваемых условиях. Зависимости на рис. 2 позволяют сделать вывод о том, что увеличение угла крутки 6 при малых начальных удлинениях приводит к росту промежутка времени t P , необходимого для достижения силой P максимального значения P max . Само значение P max практически не зависит от угла крутки. При больших удлинениях (относительное удлинение более 10%) влияние угла крутки на промежуток времени t_P весьма незначительно, но увеличение 6 приводит к некоторому увеличению максимальной силы P max .

Предложенная методика позволяет определить на только интегральную силу P , но и осевое напряжение о в каждом моноволокне. Так, для рассматриваемой мышцы ( 6 = 30°, и = 10 мм) были получены распределения напряжения по площади поперечного сечения (рис. 3) на различных стадиях изометрического возбуждения. Момент времени 5 мс соответствует достижению 1/3 от максимального значения силы P . В момент времени 100 мс увеличение силы P практически прекращается ( t P = 100 мс).

Кроме того, на рис. 3 представлено распределение по площади поперечного сечения мышцы напряжения о _п, обусловленного вязкоупругим сопротивлением материала моноволокон на сжатие. Это напряжение определяется начальной растягивающей деформацией моноволокон (7) о _п = H е| t = 0 . Использование в последнем равенстве длительного модуля упругости ( H = 10⁴ Па) связано с тем, что активизация

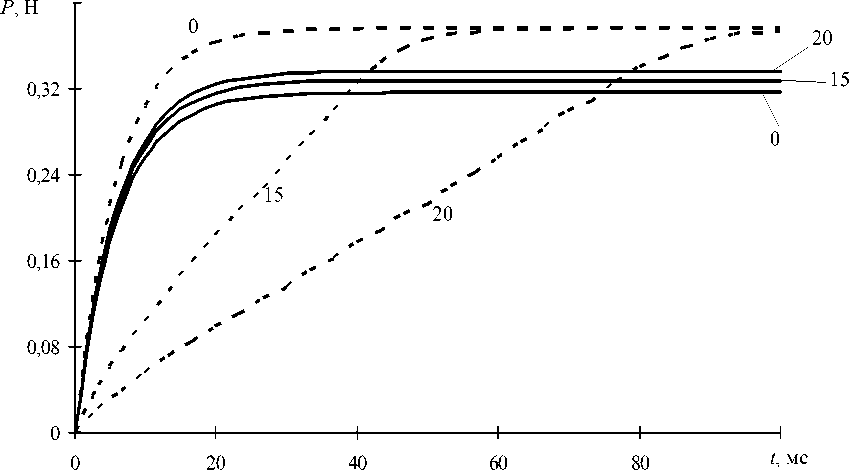
Рис. 2. Временные зависимости генерируемой мышцей силы P в изометрических условиях. Числа у кривых соответствуют значению угла крутки в градусах. Сплошные кривые построены при удлинении мышцы на u = 20 мм; пунктирные – u = 1 мм

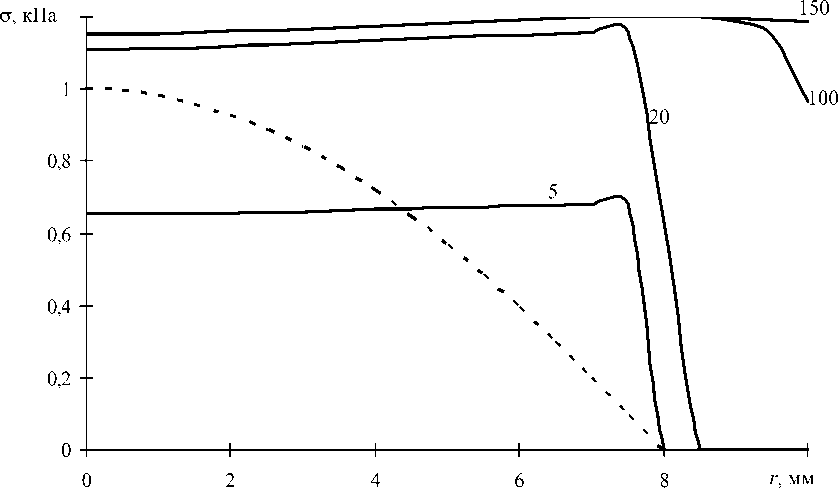
Рис. 3. Зависимость осевого напряжения σ в моноволокнах от расстояния r до оси симметрии мышцы. Числа у кривых соответствуют моменту времени в мс. Пунктиром показано напряжение σп до начала активации сократительной функции осуществляется после прекращения процесса релаксации напряжений.

Графики на рис. 3 свидетельствуют о том, что для всех моноволокон, находящихся в изометрических условиях (первая группа моноволокон), напряжение σ практически мгновенно выравнивается. Процесс завершения роста силы P приближенно соответствует распространению одинакового напряжения σ по всей площади поперечного сечения мышцы.

Заключение

Установлено, что разработанная упрощенная математическая модель сокращения мышечного моноволокна точнее по сравнению с ранее предложенной моделью «вязкоупругого стержня», описывает известные особенности деформирования мышечных тканей. Эта модель позволила выявить влияние параметров внутренней структуры (в частности, угла крутки) на процесс генерации сжимающей силы в условиях изометрического возбуждения скелетной мышцы.