Algebraic Gestalt-archetypes of Probabilities in Genomic DNAs, Cyclic Gray Codes, Quantum Bioinformatics

The concept of "gestalt" (that is, holistic form), long used in psychology, is historically known, first of all, in connection with the innate ability of a person to perceive the surrounding world as ordered holistic configurations, and not as separate fragments [1]. Due to this ability, important for survival in a changing world, the organism perceives the surrounding holistic structures constantly when the conditions of their presentation change (change in the projection of the object under consideration on the retina when changing the angle of view, change in the illumination of objects, etc.). For example, we recognize a musical melody, even if performed on different instruments and by various voices. The primary data of gestalt psychology are holistic structures (gestalt), which cannot be derived from the components that form them. It is desirable to endow robots with artificial intelligence with similar abilities of constant holistic (gestalt) perception of objects for their adequate operation, for example, on Mars in conditions of changes in the surrounding world.

The problem of holistic structures in biology is not limited to psychology. In particular, the genetically inherited human body is the holistic structure (gestalt), despite the constant cyclic renewal of its cells, proteins, etc. [2]. For example, our body's proteins are engaged in continuous life-death cycles of assembling and disassembling them into amino acids; for instance, the half-life of the hormone insulin is 6-9 minutes. In other words, parts of our body cyclically die and are reborn again while maintaining the holistic of the body's shape. For this reason, the famous physiologist A.G. Gurvich pointed out that the main problem of biology is maintaining shape under constant renewal of the substrate [3]. In other words, the problem of gestalt (the holisticy under component change) of genetically inherited structures is the main problem of biology, the study of the genetic foundations of which is the subject of the presented work.

A good example of the holisticy of the human body scheme is provided by the physiology of the so-called phantom sensations of those body parts (e.g. limbs) that are absent in some people from birth. In such cases, people, who have no personal experience of using these missing body parts, feel them as existing with phantom pains in them [4, 5]. These facts indicate that an individual's idea of the spatial scheme of his body is not at all conditioned by his life experience of using his body but is innate. This example of an innate idea of the scheme of the human body is useful to remember when discussing the innate abilities and settings of our body. Such facts of innate spatial knowledge in living organisms cannot in principle be explained based on the widespread understanding of the genetic informatics system, according to which it only determines the sequence of amino acids in proteins using the sequence of triplets in DNA and RNA molecules. When analyzing the problem of biological gestalts, it is also necessary to take into account that each living organism is a genetically encoded multilayered ensemble of coordinated cyclic processes at all its levels, and its molecular-genetic coding system is structurally linked to Gray's cyclic codes according to the data of work [2] (a brief reminder of Gray's codes is given in Appendix 1).

In the cells of an organism, individual molecules interact stochastically, and many processes in living bodies are also stochastic. It is not without reason that one of the founders of quantum mechanics and the author of the first article on quantum biology, P. Jordan, claimed that the laws of living organisms that science has missed are the laws of probability [6]. Genetics as a science began precisely with the statistical analysis of data on the inheritance of alternative traits when crossing organisms, undertaken by G. Mendel, as a result, he formulated the genetic rules of segregation (splitting) of inheritance. It can be assumed that the biological problem of inherited gestalt (i.e. the main problem of biology according to A.G. Gurvich) is somehow connected with the statistical features of genetic informatics.

The purpose of this article is to present the results of the author's study of the statistical (probabilistic) organization of nucleotide sequences in single-stranded genomic DNAs of higher and lower organisms, as well as the supposed connection of this organization with the genetic inheritance of many coordinated cyclic processes in organisms. In the course of this study, many mutually coordinated gestalt-like probabilistic rules were discovered in genomic DNAs, associated with cyclic Gray codes and the so-called genetic Karnaugh matrices. These statistical rules were identified by the author on the materials of a representative set of genomic DNAs and are therefore called gestalt archetypes of genomic probabilities. They are directly related to Jordan's assertion that the laws of living organisms missed by science are laws of probability [6]. All initial data on genomic DNAs were taken by the author from the publicly available GenBank website.

2.    Related Works

In bioinformatics, two Chargaff rules on statistical regularities in long DNA are known [7, 8]. The first rule states that the sums (or percentages) of purines and pyrimidines in the double helix of long DNA are practically equal, with the sum of G nucleotides equal to the sum of C nucleotides, and the sum of A nucleotides equal to the sum of T nucleotides. This rule was used to confirm the theoretical model of the DNA double helix by Crick and Watson [9]. The second Chargaff rule states that the same approximate equalities between the quantities (or percentages) of the specified types of nucleotides are fulfilled in long single-stranded DNAs; the study of the statistical regularities of such single-stranded genomic DNAs is continued in our article in connection with a new concept of the structural organization of the genetic coding system based on cyclic Gray codes and genetic Karnaugh matrices from Boolean logic algebra [2, 10]. Many authors have verified the fulfillment of this second Chargaff rule on the long single-stranded DNA of different organisms. For example, the work [11] confirmed the fulfillment of this rule in the analysis of long chromosomes of eukaryotes, bacteria, and archaea. In the work [12] the second Chargaff's rule was generalized to the case of triplet sequences. Useful reviews of the research and discussions of the second Chargaff's rule in connection with the ideas of genetic grammar are in the works [13-17].

A large number of works by various authors are also devoted to other phenomena of symmetry in the molecular system of genetic coding (in addition to the Chargaff rules), as well as to the supposed connections of genetic informatics with the formalisms of quantum informatics, new data on which are presented in this article in connection with Gray codes and genetic Karnaugh matrices. A review of these phenomena, connections, and models is available in the books [18-21].

The topic of genetic inheritance of biological patterns and structures is associated with the ancient concept of archetypes, especially known in connection with the works of the founder of analytical psychology C. Jung, and his concept of the collective unconscious. Physicist W. Pauli, the author of the "Pauli exclusion principle" in quantum mechanics, wrote an article in honor of Jung with the characteristic title "The Influence of Archetypal Ideas on the Formation of Kepler's Scientific Theories" [22]. As Pauli noted, "the process of cognition of nature ... is based, apparently, on the correspondence, the coincidence of pre-existing, internal images of human thought and external things and their essences ... These prototypes, which the soul perceives with the help of innate instinct, Kepler called archetypes. Kepler's prototypes largely coincide with the "elemental images" or archetypes introduced into modern psychology by C. G. Jung, acting as "instinctive representations" [22, p. 138]. Kepler himself, addressing his favorite author Proclus, believed: "To know means to compare what is perceived from the outside with internal ideas and to judge how much the two coincide. Proclus expressed this perfectly with the word "awakening", as if from sleep" [22, p. 145].

3.    Proposed Approach

To detect hidden statistical rules in the nucleotide sequence of any single-stranded genomic DNA, the author used his special method “Hierarchy of multilayer statistics”. According to the author’s method, such DNA is first considered as a sequence of single nucleotides C (cytosine), A (adenine), T (Timin), G (guanine), where percentages are calculated for each type of nucleotide (%C, %A, %T, %G). After this, the DNA sequence is considered as a sequence of pairs of nucleotides (that is, genetic duplets), for example, CA-TT-GA-..., where the percentage of each of the 16 types of duplets is calculated (%CC, %CA, %CG, ...). After this, the genomic sequence is considered as a sequence of triplets, then of tetraplets, etc., where percentages are calculated for each of 64 kinds of triplets (%CCC, %CGA, ...), for each of the 256 kinds of tetraplets (%CCCC, %ACCC, ...), etc. Thus, the nucleotide sequence of each genomic DNA is considered a multilayer system of layers of n-plets. In this article, the results of statistical analysis are presented only for values n = 1, 2, 3, 4.

The obtained values of the probabilities of each type of n-plets in the studied genomic DNA are inserted into (2n∙2n)-matrices (Fig. 1), called genetic Karnaugh matrices. The numberings of columns and rows in them are numbered by numbers (that is, code words) of cyclic n-bit Gray codes according to [2, 10, 23] due to the structural correspondence of the molecular system of genetic coding to the algorithmic family of cyclic Gray codes. The genetic (2n∙2n)-Karnaugh matrix is briefly referred to below as the n-bit Karnaugh matrix. In this case, a 2-bit Karnaugh matrix represents in its cells a complete alphabet of 16 duplets, a 3-bit Karnaugh matrix – a complete alphabet of 64 triplets, etc. These matrices are constructed by analogy with Karnaugh maps from Boolean algebra of logics, which use Gray codes to number columns and rows and which are an effective means of simplifying Boolean algebra expressions to minimize the number of logic gates in logical constructions []. The cells in Karnaugh maps of Boolean logic are known as minters, and each cell value represents the corresponding output value of a Boolean function. The author's appeal to genetic Karnaugh matrices provides an interesting opportunity to interpret genetic n-plets (duplets, triplets, tetraplets, etc.) as output values of Boolean functions [2, 10].

0		1		00	00	01	11	10
					сс 0.0541	СА 0.0727	АА 0.0950	АС 0.0503	0.2722
	с	А			0000	0001	ООН	0010
0	0.2085	0.2910 01	0.4995	01	СТ	CG	AG	АТ	0.2273
	Т	G			0.0713	0.0103	0.0714	0.0743
1	0.2918	0.2087	0.5005		0100	0101	0111	ОНО
	10				ТТ	TG	GG	GT
	0.5003	0.4997		и	0.0957	0.0729	0.0542	0.0505	0.2732
						1101		1110
					ТС	ТА	GA	GC
				10	0.0601	0.0631	0.0601	0.0440	0.2273
					1000		1011
					0.2812	0.2190	0.2807	0.2191

ООО 001       011       010 ПО 111       101       100

ООО	ссс 0.0138 000 000	CCA 0.0188 000001	САА 0.0186	САС 0.0152 000010	AAC 0.0145	AAA 0.0369 000111	АСА 0.0198 000101	ACC 0.0118 000100	0.1495
001	сст 0.0185 001000	CCG 0.0029 001001	CAG 0.0210 001011	CAT 0.0179 001010	AAT 0.0238 001110	AAG 0.0199 001111	ACG 0.0025 001101	ACT 0.0162 001100	0.1228
011	стт 0.0201 011000	CTG 0.0209 011001	CGG 0.0029 011011	CGT 0.0026 011010	AGT 0.0161 011110	AGG 0.0185 011111	ATG 0.0178 011101	ATT 0.0239 011100	0.1228
010	СТС 0.0176 010000	СТА 0.0127	CGA 0.0023 010011	CGC 0.0025	AGC 0.0144 010110	AGA 0.0224	ATA 0.0194 010101	АТС 0.0132	0.1045
по	ттс| 0.0197 110000	ТТА 0.0198 110001	TGA 0.0195 [110011	TGC 0.0146 110010	GGC 0.0126 110110	GGA 0.0160 110111	GTA 0.0112 110101	GTC 0.0096 110100	0.1228
111	ттт 0.0372 111000	TTG 0.0188 111001	TGG 0.0190 111011	TGT 0.0199 111010	GGT 0.0119 111110	GGG 0.0138 111111	GTG 0.0153 111101	GTT 0.0145 1111	0.1504
101	тст 0.0223 101000	TCG 0.0023 101001	TAG 0.0128 101011	TAT 0.0194 101010	GAT 0.0133 101110	GAG 0.0176 101111	GCG 0.0025 101101	GCT 0.0144 101100	0.1046
100	тсс 0.0159 100000	ТСА 0.0196	TAA 0.0199 100011	TAC 0.0110	GAC 0.0096 100110	GAA 0.0196	GCA 0.0146 100101	GCC 0.0125	0.1227
	0.1652	0.1159	0.1160	0.1031	0.1161	0.1646	0.1031	0.1160

Fig.1. The location of nucleotides, their duplets, and triplets in genetic (2n*2n)-matrices of Karnaugh (they are given in bold frames with the numbers of their columns and rows according to n-bit Gray's codes). The percentage of each n-plet in the n-plet layers of the DNA first human chromosome is shown. On the right and below each matrix, the sums of all percentages of n-plets in each row and column are shown. Cells with even numbers are highlighted in black color (explanation in the text).

The construction of genetic Karnaugh matrices uses the phenomenological fact that the DNA alphabet of 4 nucleotides C, A, T, and G is the carrier of the system of binary-oppositional features: 1) two of these nucleotides are purines (A and G), having 2 rings in their molecule, and the other two nucleotides (C and T) are pyrimidines with 1 ring in the molecule, which gives the representation C = T = 0, A = G = 1; 2) two of these nucleotides are keto-molecules (T and G), and the other two (C and A) are amino-molecules, which gives the representation C = A = 0, T = G = 1. Due to this, DNA alphabets of 4 nucleotides, 16 duplets, 64 triplets, etc. are represented in the form of a family of square matrices, the columns of which are numbered by the opposition features “purine or pyrimidine” (C = T = 0, A = G = 1), and the rows - by the opposition features “amino or keto” (C=A=0, T=G=1), and the numberings are ordered by members of n-bit Gray codes (Fig. 1). Each member of these DNA alphabets occupies a strictly defined cell in the family of square matrices.

The numbers of each cell in these matrices with a certain n-plet in it are formed by concatenating those numbers of the corresponding n-bit Gray code, which numbers the row and column of this cell (correspondingly the numbers of cells become numbers of the 2n-bit Gray code). A pair of columns (rows) in genetic n-bit Karnaugh matrices is called complementary in the sense of their Gray code numbers if their numbers transform into each other when the symbols 0↔1 are mutually replaced (the complementarity operation about numbers of Gray codes). For example, in a 3-bit Karnaugh matrix, columns with numbers 001 and 110 are complementary.

In Fig. 1, each matrix cell shows the symbol of the corresponding n-plet, its number from 2n-bit Gray code, and its percentage (accurate to the fourth decimal place) in the corresponding n-plet layer of the nucleotide sequence of singlestranded DNA of human chromosome №1. This human chromosomal DNA, used in the data in Fig. 1 as an example of the genomic DNAs, contains approximately 250 million nucleotides. Its original characteristics are taken from the GenBank website . Cells with Gray code numbers that correspond to even decimal numbers are highlighted in black in contrast to cells of odd decimal numbers highlighted by white; in genetic Karnaugh matrices, it defines a mosaic of a chessboard type.

4.    Computational Experiment

At first glance, these genetic matrices of Karnaugh in Fig. 1 contain a chaotic set of percent of n-plets. However, the analysis conducted by the author revealed a whole series (or a web) of regular fractal-like interrelationships in this multilayer probability system, which are also realized on many other genomic DNAs analyzed by the author. Some of such interrelations are associated with the concept of complementary columns (rows) in the genetic matrices of Karnaugh: any pair of columns (or rows), whose numberings in these matrices pass into each other under a mutual replacement of 0↔1, are called complementary about Gray code numbers. For example, columns with numbers 100 and 011 from the Gray code complement each other. We proceed to describe the identified rules of the stochastic-deterministic organization of nucleotide sequences in genomic DNAs.

Rule 1. (about the algebraic gestalt-archetype of equality of the summary probabilities in some pairs of n-plet groupings in the n-plet layer of genomic DNA). The first identified genomic rule of probabilities in the n-plet layer of the genomic DNA is that, in the corresponding n-bit Karnaugh matrix, the summary probabilities of the n-plets in the columns (rows), which are complementary in the relation of Gray code numbers, are practically equal (Table 1), although the sets of probabilities of individual n-plets in their composition are different. For example, in DNA human chromosome №1, in the genetic 4-bit Karnaugh matrix for duplets (Fig. 1), complementary rows with Gray numbers 01 and 10, containing 4 different duplets with different probabilities for each, have practically equal sums of probabilities 0.2273 of their four duplets (1):

(The row 01): %CT+%CG+%AG+%AT = 0.0713+0.0103+0.0714+0.0743 = 0.2273,

(The row 10): %TC+%TA+%GA+%GC = 0.0601+0.0631+0.0601+0.0440 = 0.2273 (1)

Similarly, in the 6-bit Karnaugh matrix for triplets (Fig. 1), the complementary columns with Gray numbers 001 and 100, containing 8 different triplets with different probabilities for each, have the same sum of probabilities 0.1160 of their 8 triplets (2):

(The column 011): %CAC+%CAG+%CGG+%CGA+%TGA+%TGG+%TAG+%TAA = = 0.0186+0.0210+0.0029+0.0023+0.0195+0.0190+0.0128+0.0199 = 0.1160;

(The column 100): %ACC+%ACT+%ATT+%ATC+%GTC+%GTT+%GCT+%GCC =

= 0.0118+0.0162+0.0239+0.0132+0.0096+0.0145+0.0144+0.0145 = 0.1160 (2)

Each genetic n-bit Karnaugh matrix is a set of such gestalt-archetypal relations between complementary columns, as well as between complementary rows (in the sense of n-bit Gray code). This unexpected equality of genomic probabilities in such complementary columns (rows) is called by the author the term "gestalt of probabilities", meaning the overall holistic structure of summary probabilities with a significant difference in the probabilities of terms of the sum. The use of this term (known primarily in psychology and biology), along with or instead of the simple term "numerical regularity", expands the significance of statistical regularities revealed in genomic informatics. The term links these statistical regularities with extensive factual materials of gestalt psychology and other long-studied sciences of consciousness, which have not yet been associated with the statistical features of genomic DNAs.

This rule works for different genomic DNAs studied by the author:

• •    all 24 types of human chromosomes;

• •    all chromosomes of Drosophila, mice, worms, and many plants;

• •    19 genomes of bacteria and archaea;

• •    many extremophiles live in extreme conditions, such as radiation levels 1000 times higher than the lethal level for humans (a list of genomes studied by the author in connection with different problems of matrix genetics is given in [24]).

Therefore, we speak of algebraic gestalt archetypes of probabilities in genomic DNAs, briefly calling them in the case of Rule 1 "gestalt-archetypes of complementarity of genomic probabilities".

Table 1 shows the gestalts of complementarity of probabilities for different types of binary oppositions "purines-pyrimidines" and "amino-keto" that determine the numbering of columns and rows. In it, the symbols, for example, %100 and %011 denote the sums of percentages of all triplets in complementary columns numbered with Gray numbers 100 and 011 and containing all triplets of the type "pyrimidine-purine-purine" and "purine-pyrimidine-pyrimidine". The symbols %100 and %011 denote the sums of percentages of all triplets in complementary rows numbered with the same Gray numbers and containing, respectively, all triplets of the type "keto-amino-amino" and "amino-keto-keto".

Table 1. Practical equality of the values of summary probabilities of n-plets in pairs of complementary rows and complementary columns of n-bit karnaugh matrices from fig. 1

n	Sums of probabilities in complementary columns	Sums of probabilities in complementary rows
1	%0 (= 0.5003 ) ≈ %1 (= 0.4997 )	%0 (= 0.4995 ) ≈ %1 (= 0.5005 )
2	%00 (= 0.2812 ) ≈ %11 (= 0.2807 );	%00 (= 0.2722 ) ≈ %11 (= 0.2732 );
	%01 (= 0.2190 ) ≈ %10 (= 0.2191 );	%01 (= 0.2273 ) ≈ %10 (= 0.2273 )
	%000 (= 0.1652 ) ≈ %111 (= 0.1646 );	%000 (= 0.1495 ) ≈ %111 (= 0.1504 );
3	%001 (= 0.1159 ) ≈ %110 (= 0.1161 );	%001 (= 0.1228 ) ≈ %110 (= 0.1228 );
	%011 (= 0.1160 ) ≈ %100 (= 0.1160 );	%011 (= 0.1228 ) ≈ %100 (= 0.1227 );
	%010 (= 0.1031 ) ≈ %101 (= 0.1031 )	%010 (= 0.1045 ) ≈ %101 (= 0.1046 )
	%0000 (= 0.0982 ) ≈ %1111 (= 0.0977 );	%0000 (= 0.0830 ) ≈ %1111 (= 0.0838 );
	%0001 (= 0.0669 ) ≈ %1110 (= 0.0669 );	%0001 (= 0.0664 ) ≈ %1110 (= 0.0666 );
	%0011 (= 0.0605 ) ≈ %1100 (= 0.0604 );	%0011 (= 0.0659 ) ≈ %1100 (= 0.0648 );
4	%0010 (= 0.0555 ) ≈ %1101 (= 0.0556 );	%0010 (= 0.0569 ) ≈ %1101 (= 0.0580 );
	%0110 (= 0.0490 ) ≈ %1001 (= 0.0490 );	%0110 (= 0.0563 ) ≈ %1001 (= 0.0563 );
	%0111 (= 0.0669 ) ≈ %1000 (= 0.0670 );	%0111 (= 0.0666 ) ≈ %1000 (= 0.0664 );
	%0101 (= 0.0475 ) ≈ %1010 (= 0.0476 );	%0101 (= 0.0466 ) ≈ %1010 (= 0.0476 );
	%0100 (= 0.0556 ) ≈ %1011 (= 0.0555 )	%0100 (= 0.0579 ) ≈ %1011 (= 0.0570 )

Regarding decimal equivalents of Gray code numbers, the numberings in each pair of Gray complementary columns (rows) of Karnaugh matrices correspond to a pair of decimal digits, one of which is even and the other odd. Taking this into account, one can note the existence of the following corollary to Rule 1:

• •    in genetic n-bit Karnaugh matrices for genomic DNAs, the sums of the probabilities of n-plets in all columns (rows) with decimal even numbers and with decimal odd numbers are practically equal. This can be considered a gestalt archetype of genomic probabilities of the "even-odd" type, echoing the long-standing theme of the difference in the functions of the two hemispheres of the brain, as well as the "even-odd" binary of the basic codes of human culture and the theory of dialogue, described in the book translated into many languages [25].

When moving from an n-plet layer to the next (n+1)-plet layer in genomic DNAs, the number of polyplet kinds in the columns (and rows) doubles (Fig. 1). In this case, in genomic DNAs, between the n-bit Karnaugh matrix and the (n+1)-bit Karnaugh matrix, regular dichotomous relationships of the total probabilities of the polyplets of the columns (and rows) are realized, expressed by the following two rules.

Rule 2. For genomic DNA in its Karnaugh (2n∙2n)-matrix, each column (row) has such a total probability of all its n-plets, which is practically equal to the sum of the total probabilities of two columns (rows) in the Karnaugh (2n+1∙2n+1)-matrix. For example, in Fig. 1 in the Karnaugh matrix for duplets, column number 01 has a probability of 0.2190, and in the Karnaugh matrix for triplets, two columns with numbers 010 and 011 have almost the same sum of their total probabilities 0.2191 (= 0.1160+0.1031).

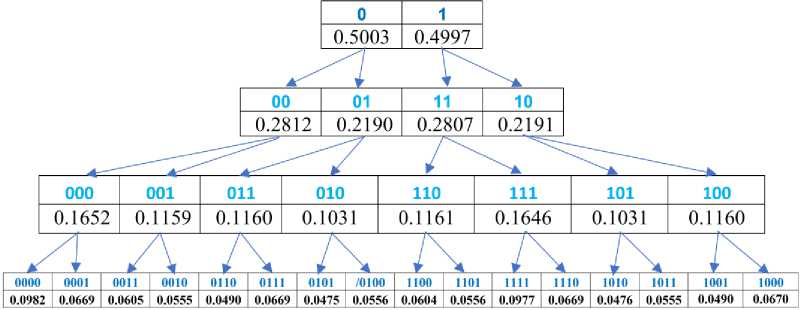
Fig.2. Graphical illustration of Rule 2 on the dichotomous relationship between the sums of probabilities in columns and rows of the n-bit and (n+1)-bit Karnaugh matrices (n = 1, 2, 3, 4). The top line illustrates this dichotomy for columns and the middle line for rows of the Karnaugh matrices. The bottom row shows a fractal dichotomous tree of this interrelationship. Percentage values are given for the case of DNA of human chromosome № 1

Rule 3. In genomic DNAs and their genetic Karnaugh matrices, any pair of complementary columns (rows) in its n-plet layer corresponds to two pairs of complementary columns (rows) in the (n+1)-plet layer with practically equal summary probabilities of (n+1)-plets in each of them. For example as Fig. 1 shows, a pair of complementary columns with Gray numberings 01 and 10 (they have practically equal summary probabilities 0.2190 and 0.2191) in the Karnaugh matrix for duplets corresponds - in the Karnaugh matrix for triplets - to two pairs of complementary columns with numberings 011 and 100 (they have practically equal summary probabilities of 0.1160, although the percentages of individual triplets in them are different) and numberings 010 and 101 (they also have practically equal summary probabilities of 0.1031, although the percentages of individual triplets in them are different). Briefly, we call this algebraic regularity the "gestalt archetype of segregation of complementary summary probabilities." This dichotomous segregation of sums of probabilities in complementary columns and rows is accompanied by the formation of two dichotomous fractal trees of probabilities, in which each column and each row serves as the beginning of its fractal tree.

Another genomic archetypal gestalt of probabilities in the family of genetic n-bit Karnaugh matrices, corresponding to the multilayer system of n-plet layers of genomic DNAs, is associated with the equality of the sums of probabilities of n-plets in those of their groupings that are characterized by the location of a certain nucleotide, called attributive, at a certain position in n-plets (under a fixed value of n). For example, if cytosine C acts as an attribute, then the TCA triplet has an attribute nucleotide in the second position, and the GTC triplet in the third position. In genomic DNAs, the following rule expresses the regular relationship between the sums of probabilities in those n-plet groupings, which are determined by the feature of the same attribute nucleotide at the same position of n-plets.

Rule 4. In genomic DNAs, the percentage of each of the nucleotide’s C, G, A, and T is practically equal to the sum of the percentages of all those duplets, as well as triplets and tetraplets, in which the attributive nucleotide is located at the same fixed position (at first, or second, or third, or fourth), though the numbers of n-plets and the probability values of individual n-plets are significantly different. The author calls this algebraic regularity of genomic DNAs the "archetypal gestalt of the summary probabilities of n-plets with a positioned attribute."

Table 2 shows a numerical example of the implementation of this rule in the case of genetic n-bit Karnaugh matrices for the DNA of the human chromosome № 1. The symbols used in the Table can be explained by using the example of the symbol ∑NCNN: it denotes a grouping of all 4 tetraplets in which the attributive nucleotide C is located in the second position, and all other positions are occupied by some of the 4 types of nucleotides C, G, A, T.

Table 2. Percentages of nucleotides C, G, A, T and sums Σ of percentages of all n-plets with these nucleotides at indicated positions in genetic n-bit Karnaugh matrices for the case of DNA of the human chromosome № 1 (Fig. 1). The symbol N denotes any of these nucleotides

%C = 0.2085	%G = 0.2087	%A = 0.2910	“AT = 0.2918
PACN= 0.2085	S%GN = 0.2088	E%AN = 0.2910	PATN»0.2917
PANC ~ 0.2085	PANG = 0.2087	PANA» 0.2910	PANT = 0.2918
S%CNN «0.2084	S%GNN « 0.2088	Z%ANN « 0.2910	S%TNN « 0.2917
S%NCN « 0.2085	S%NGN « 0.2088	Z%NAN == 0.2910	E%NTN « 0.2917
S%NNC « 0.2085	S%NNG « 0.2087	PANNA» 0.2910	Z%NNT « 0.2918
£%CNNN » 0.2085	S%GNNN * 0.2088	S%ANNN » 0.2910	£%TNNN » 0.2917
2%NCNN « 0.2085	£%NGNN « 0.2087	Z%NANN » 0.2910	S%NTNN » 0.2918
S%NNCN « 0.2085	S%NNGN « 0.2088	Z%NNAN « 0.2910	E%NNTN * 0.2918
E%NNNC = 0.2085	PANNNG = 0.2087	PANNNA = 0.2910	PANNNT = 0.2918

Knowing the percentages of %A, %T, %C, and %G nucleotides in a 1-bit genetic Karnaugh matrix (i.e., in a 1-bit text representation of a genomic DNA), one can predict with impressive accuracy the sums of the percentages of n-plets in n-bit Karnaugh matrices for n = 2, 3, 4, …, i.e., percetages in the groupings shown in Table 2: in 4 groupings of duplets (4 duplets per each of the groupings), 4 groupings of triplets (16 triplets per each of the groupings), 4 groupings of tetraplets (64 tetraplets per each of the groupings), etc. The possibility of such predictions is realized not only for the considered DNA of the human chromosome № 1 but also for many genomic DNAs of eukaryotes and prokaryotes that have been analyzed in the author's laboratory to date. Note that the nucleotide percentages of %A, %T, %C, and %G can vary greatly may differ in different genomes when the same archetypal rules of summary probabilities are fulfilled in the above-indicated cooperative parts of the genomes as a whole. For example, the genomic DNA of the bacterium Bradyrhizobium japonicum contains %A≈0.1819, %T≈0.1815, %C≈0.3184, and %G≈0.3182, unlike the DNA of the human chromosome № 1 considered above. This demonstrates the universal cooperative organization of the probabilistic compositions of n-plet groupings in genomic DNA texts, which are associated with genetic n-plet Karnaugh matrices and cyclic Gray codes.

In the Karnaugh matrices in Fig. 1, n-plets, having a certain attributive nucleotide in the first position, are placed in each of the 4 quadrants. For example, in the left upper quadrant of each matrix, all n-plets with the nucleotide C in the first position are placed. However, if we perform cyclic shifts of digital positions in the members of cyclic Gray codes (that identify the rows and columns of the Karnaugh matrices) then such rearrangement of the arrangement of n-plets in the matrices occurs that in each quadrant of the matrices, all its n-plets have the same attributive nucleotide, but in shifted position, for example, in the second position, etc. This opportunity of regular repositions of the cyclic kind for n-plet ensembles additionally emphasizes the structural connection of the genetic coding system with cyclic Gray codes and the genetic family of n-bit Karnaugh matrices.

• 4.1.    Questions of Quantum Bioinformatics

The rules of probability segregation in the statistical organization of information sequences of genomic DNAs of higher and lower organisms that we have discovered and presented above allow us to make significant progress in modeling and understanding the features of genetic informatics from the standpoint of quantum informatics formalisms (this line of research is aimed, among other things, at developing the foundations of genetic statistical biomechanics). Let us present this in more detail.

The key concept of quantum information science is the concept of a qubit [26]. It is considered as a quantummechanical system whose state is described by vectors of a 2-dimensional Hilbert space in the form (3):

|Ψ> = α|0> + β|1> (3)

where the vectors |0> and |1> form an orthonormal basis and are called computational basis quantum states. The coefficients at them are called their probability amplitudes (they are equal to the square root of the probability of these states), satisfying the condition |α|2 + |β|2 = 1. In quantum computing, n-qubit systems are also used for values of n = 2, 3, and more. Engineers all over the world are striving to create quantum computers with an increased number of qubits, overcoming significant technical difficulties. While a classical computer can be in exactly one of the states |0>, |1>, …, |n-1> (these are Dirac notations), a quantum processor is simultaneously in all of these basis states at any given moment, which provides certain computational advantages. A system of n qubits has a correspondingly increased number 2n of basis quantum states, equal to the number of members in the dyadic n-bit group of binary numbers or in the n-bit Gray code. Since Gray code numbers and binary numbers are algorithmically converted into each other at the same bit depth, below we will continue to use Gray code numbers in the model representation of the statistical features of nucleotide sequences of genomic DNA in the form of 22n-qubit systems (since n-bit Karnaugh matrix has 22n cells).

22n-member sets of probabilities of n-plets in genetic Karnaugh matrices (n = 1, 2, 3, …) can be formally written as corresponding 22n-qubit systems of quantum information science. In each such system, the sequence of computational basis states can be written in the order of terms of n-bit Gray codes, considering the known works on similar applications of Gray codes in quantum computing. According to works [27, 28], such use of Gray codes in quantum information science gives certain advantages due to the following. Optimal implementation of quantum gates is crucial for designing a quantum computer. Work [27] considers the matrix representation of an arbitrary multi-qubit gate using Gray codes. Ordering the basis vectors using the Gray code allows one to construct a quantum circuit that is optimal in the sense of fully controllable single-qubit gates and at the same time equivalent to a multi-qubit gate. In this case, the second stage of optimization removes unnecessary control bits, which ultimately leads to a smaller total number of elementary gates. The work [28] reveals the potential of using Gray codes in quantum computing applications for modeling a variety of quantum systems in physics and chemistry. The results and procedures described therein are aimed at modeling a wide class of Hamiltonians on digital quantum computers based on qubits.

In our work, for example, the systems of 4 nucleotides, 16 duplets and 64 triplets with the indicated probabilities in the nucleotide sequence of the studied single-stranded DNA (shown in Fig. 1 in the Karnaugh matrices) are characterized by quantum states that are written in the form of the system (4), where, for the computational base states, the probability amplitudes of the corresponding n-plets of this DNA are indicated, and these states themselves are shown in accordance with the order of the 2-bit Gray code:

|Ψ 2 > = √%C |00 > + √ %A |01> + √%G |11> + √% T |10>,

|Ψ 4 > = √% СС |0000> + √% CA |0001> + √%AA |0011> + √% AC |0010> +

√ % AT |0110> + √ %AG |0111> + √ %CG |0101> + √ %CT |0100> + √ %TT | 1100> + √ %TG | 1101> + √ %GG | 1111> + √ %GT | 1110> + √%GC |1010> + √%GA |1011> + √%TA |1001> + √%TC |1000>                   (4)

These quantum information vectors of the Hilbert spaces |Ψ 2 > and |Ψ 4 >, whose coordinates are the probability amplitudes, have unit length since it represents the total probability of the corresponding n-plets.

The states of single-stranded DNAs, considered as state vectors of their sequences of triplets of 64 types |Ψ 6 >, of tetraplets of 256 types |Ψ 8 >, etc., are written similarly. In the case of genomic DNAs, all these states |Ψ 2 >, |Ψ 4 >, |Ψ 6 >, |Ψ 8 >, etc. turn out to be interconnected due to the rules of genomic probabilities (archetypal gestalts of probabilities) identified and described above. In other words, in our model approach, the information sequence of nucleotides of each genomic DNA appears as a holistic multilayer network (or web) of quantum-information ensembles, where each n-th text layer is represented by its 2²ⁿ-qubit system, and different n-plets layers are interconnected by universal rules of segregation of genomic n-plets probabilities. Changes in the state of one layer of this multilayer web affect the state of all other layers connected to it. This is associated with a powerful collectivism in the organization of a genetically inherited living body consisting of many interconnected parts. This may be one of the reasons for the amazing noise immunity of the genetic coding system.

Such a multilayer genomic quantum information network, having fractal-like structures and regular internal connections between n-plet layers, is fundamentally different from single-layer n-qubit systems traditionally used in modern quantum computing. Therefore, the author suggests using the short name "fractal quantum bioinformatics" for such genomic multilayer quantum informatics. It can be assumed that the development of engineering schemes of quantum computing will eventually come to the wide use of the principles of this fractal quantum bioinformatics for artificial intelligence systems and other digital computer technologies. At the same time, the tradition of scientific and technological progress will be continued, when the properties of bio-organisms served as prototypes of engineering solutions (for example, the ability of birds to fly served as a prototype of airplanes).

The rules of probability segregation in the stochastic-deterministic organization of information sequences of genomic DNAs of higher and lower organisms, discovered by the author and presented above, allow for significant advances in modeling and understanding the features of genetic informatics from the standpoint of formalisms of quantum informatics (this area of research is also aimed at developing the foundations of genetic statistical biomechanics).

• 4.2.    Genetic Karnaugh Matrices and Hydrogen Bonds

Single-stranded DNAs are linked into a DNA double helix by hydrogen bonds in complementary base pairs: nucleotides C and G are connected by three hydrogen bonds, and nucleotides A and T by two hydrogen bonds. Due to this, we have the following numerical representation of these nucleotides: C=G=3, A=T=2. Of all the chemical bonds of biomolecules for living bodies, the most important type is the hydrogen bond. In particular, two-time Nobel laureate L. Pauling believed that with further application of the methods of structural chemistry to physiological problems, it would be discovered that the significance of the hydrogen bonds for physiology is greater than the significance of any other individual structural feature [29]. Hydrogen bonds arising between carbonyl and amino groups >C=O---H-N< determine the structure of proteins, nucleic acids, and other biologically important molecules. The author believes that the stochastic-deterministic protosystem of biological regulation is built to a high degree on systems of hydrogen bonds and their associations with soliton-like structures [30, 31]. Hydrogen bonds determine many properties of water and ice. The wealth of emergent properties of hydrogen bond systems can be illustrated by the example of jellyfish, which are 98% water, representing, figuratively speaking, a complex-shaped bag with a water substrate of hydrogen bonds. At the same time, jellyfish are the most ancient multicellular animals on Earth with a huge evolutionary diversity of species and functional capabilities, including the ability to reproduce sexually and asexually. We will add that hydrogen is the most common element in the Universe: it accounts for about 88.6% of all atoms.

Let us now show that the named system of hydrogen bonds of complementary DNA bases is algebraically related to the family of genetic n-bit Karnaugh matrices and to Gray codes. Each nucleotide n-plet of DNA, when each of its letter symbols is replaced by its inherent number of hydrogen bonds (C = G = 3, A = T = 2), receives a "hydrogen index" in the form of a binary n-plet consisting of the numbers of its hydrogen bonds of two types - 2 and 3 -, written in the sequence of nucleotides of a given n-plet. For example, the nucleotide duplet CA is represented by a duplet index of 32 hydrogen bonds, and the triplet TGC - by a triplet hydrogen index of 233. In such a hydrogen-numerical binary representation, various DNA n-plets are combined into separate equivalence classes by identical hydrogen indices. For example, the equivalence class of duplets with the hydrogen index 32 contains 4 duplets CA, CT, GA, GT, and the equivalence class of triplets with the hydrogen index 333 contains 8 triplets CCC, CCG, CGG, CGC, GCC, GGC, GCG, GGG. In genomic DNA, each of these n-plets equivalence classes by hydrogen index has a certain percentage (probability) of occurrence of the n-plets included in it. This percentage is equal to the sum of the percentages of all n-plets included in this class. For example, the equivalence class with the hydrogen index 32 has a percentage of %32 = %CA+%CT+%GA+%GT. The set of n-plets for a fixed n consists of 2^n equivalence classes by hydrogen indices. For example, the set of 16 duplets consists of 22 = 4 equivalence classes with hydrogen indices 33, 32, 22, 23, and the set of 64 triplets consists of 23 = 8 equivalence classes with hydrogen indices 333, 332, 322, 323, 223, 222, 232, 233. In Fig. 3, the indices of these hydrogen equivalence classes are listed in such an order that the Hamming distance between adjacent members of their sequence is 1, i.e., each of these numbered sequences of hydrogen n-plet indices represents an analog of cyclic n-bit Gray code. This becomes especially clear if (in the binary notations of the indices) the symbol 3 is replaced by the binary symbol 0, and the symbol 2 by the binary symbol 1; then, for example, the sequence of 2-bit hydrogen indices 33, 32, 22, 23 is transformed into the 2-bit Gray code 00, 01, 11, 10. The use of such a sequence shows below in Fig. 3 the regular relationship of genomic probabilities between sets of n-plet hydrogen equivalence classes with different values n.

In single-stranded genomic DNA, the percentage of each equivalence class of n-plets with the same hydrogen index is equal to the sum of the probabilities of the n-plets that make it up. For example, for duplets with a hydrogen index of 32, their hydrogen equivalence class has a percentage of %32, which is equal to the sum of the percentages in this DNA of all 4 duplets that make it up: %32 = %CA+%CT+%GA+%GT. The author has found that there is a regular dichotomous relationship between the percentages of different n-plet equivalence classes, which is graphically presented in Fig. 3 and forms the basis of the Rule 5 on the gestalt-archetype of genomic probabilities for hydrogen bonds.

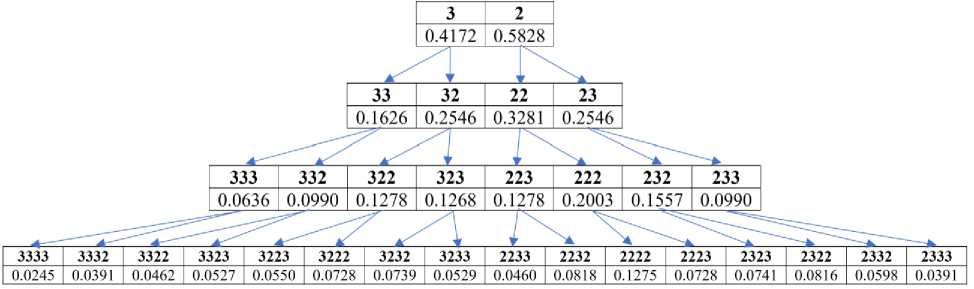
Fig.3. Illustration of the genomic gestalt-archetype of the dichotomous relationship of probabilities between classes of n-plets equivalent in hydrogen bond indices. The top line of each row shows the hydrogen indices of the n-plet equivalence classes, and below it is the probabilities of the corresponding class in the DNA of the human chromosome № 1 (values rounded to the fourth decimal place). In each sequence of hydrogen indices, the Hamming distance between adjacent members is 1 (see text for explanation)

From Fig. 3, using the example of DNA of the human chromosome № 1, it can be seen that the genomic probability of each class of hydrogen equivalence of n-plets (called the initial) is equal with high accuracy to the sum of the probabilities of two classes of hydrogen equivalence of (n+1)-plets, the hydrogen index of which is obtained by adding the suffixes 3 and 2 to the hydrogen index of the initial n-plet class. For example, the probability of the equivalence class of monoplets with the hydrogen index 3, i.e. %3 = 0.4172, coincides with the sum of the probabilities of two equivalence classes of duplets 33 and 32: %33+%32 = 0.1626+0.2546 = 0.4172. The probability of the equivalence class of duplets with the hydrogen index 32, i.e. %32 = 0.2546, coincides with the sum of the probabilities of two equivalence classes of triplets with hydrogen indices 322 and 323: %322+%323 = 0.1278+0.1268 = 0.2546, and so on. As a result, there is a fractal dichotomous tree of probabilities of such equivalence classes by hydrogen index. In this dichotomous tree, the probability of each class is the vertex of its fractal tree (the author systematically checked this for different genomic DNAs under values n = 1, 2, 3, 4, and also selectively and fragmentarily under n = 5, 6 and more).

Rule 5. (on the genomic gestalt-archetype of the dichotomous relationship of genomic probabilities in the case of equivalence classes by hydrogen indices). In genomic DNA, the probability of each equivalence class of n-plets by hydrogen index is practically equal to the sum of the probabilities of two equivalence classes of (n+1)-plets, the hydrogen indices of which differ from the hydrogen index of the initial class using additional suffixes 3 and 2 to it.

The data in Fig. 3 draw attention to another regularity: two equivalence classes, whose hydrogen indices pass into each other when the direction of their reading is reversed (from right to left and from left to right), have practically identical genomic probabilities (this can be interpreted as a special type of complementarity). Expressions (5) explain this.

%32=0.2546 я %23=0.2546; %332=0.0990 г %233=0.0990; %322=0.1278 г %223=0.1278;

%3332=0.0391 г %2333=0.0391; %3322=0.0462 г %2233=0.0460;

%3323=0.0527 г %3233=0.0529; %3222=0.0728 г %2223=0.0728;

%3232=0.0739 г %2323=0.0741; %2232=0.0818 г %2322=0.0816 (5)

This regularity can be represented as the following gestalt-archetype of genomic probabilities.

Rule 6. (on the gestalt-archetype of genomic probabilities for equivalence classes of n-plets by hydrogen bond indices). In genomic DNA, two equivalence classes of n-plets by hydrogen bond indices have practically the same probabilities if their probability indices are transformed into each other when reversing their reading (from right to left and from left to right).

Representing each n-plet by its hydrogen bond index in the genetic n-bit Karnaugh matrices in Fig. 1 (for example, each of the 4 doublets CA, CT, GA, GT is represented by the hydrogen index 32 or the percentage %32 of the equivalence class of doublets with this index), we obtain the bisymmetric n-bit Karnaugh matrices of hydrogen equivalence classes in Fig. 4. Each cell shows the hydrogen equivalence class and its percentage in the considered DNA of the human chromosome № 1. Each row and each column of these (2n-2n) matrices represents the entire set of 2n equivalence classes, and the sum of the probabilities of such a set is equal to 1.0 (i.e. 100%).

0	1
%3 = 0.4172	%2 = 0.5828
%2 = 0.5828	%3 = 0.4172

	00	01	11	10
00	%33= 0.1626	%32= 0.2546	%22= 0.3281	%23= 0.2546
01	%32= 0.2546	%33= 0.1626	%23= 0.2546	%22= 0.3281
11	%22= 0.3281	%23= 0.2546	%33= 0.1626	%32= 0.2546
10	%23= 0.2546	%22= 0.3281	%32= 0.2546	%33= 0.1626

	000	001	Oil	010	110	111	101	100
000	%333= 0.0636	%332= 0.0990	%322= 0.1278	%323= 0.1268	%223= 0.1278	%222= 0.2003	%232= 0.1557	%233= 0.0990
001	%332= 0.0990	%333= 0.0636	%323= 0.1268	%322= 0.1278	%222= 0.2003	%223= 0.1278	%233= 0.0990	%232= 0.1557
Oil	%322= 0.1278	%323= 0.1268	%333= 0.0636	%332= 0.0990	%232= 0.1557	%233= 0.0990	%223= 0.1278	%222= 0.2003
010	%323= 0.1268	%322= 0.1278	%332= 0.0990	%333= 0.0636	%233= 0.0990	%232= 0.1557	%222= 0.2003	%223= 0.1278
110	%223= 0.1278	%222= 0.2003	%232= 0.1557	%233= 0.0990	%333= 0.0636	%332= 0.0990	%322= 0.1278	%323= 0.1268
111	%222= 0.2003	%223= 0.1278	%233= 0.0990	%232= 0.1557	%332= 0.0990	%333= 0.0636	%323= 0.1268	%322= 0.1278
101	%232= 0.1557	%233= 0.0990	%223= 0.1278	%222= 0.2003	%322= 0.1278	%323= 0.1268	%333= 0.0636	%332= 0.0990
100	%233= 0.0990	%232= 0.1557	%222= 0.2003	%223= 0.1278	%323= 0.1268	%322= 0.1278	%332= 0.0990	%333= 0.0636

Fig.4. Example of genetic n-bit Karnaugh matrices of genomic probabilities in the case of equivalence classes of n-plets, having the same hydrogen bond index. In each cell, the percentage of the corresponding equivalence class in the DNA of the human chromosome № 1 is indicated

Dyadic-shift decompositions of each of the Karnaugh matrices in Fig. 4 reveal the following. The 2-bit Karnaugh matrix for two nucleotide equivalence classes with hydrogen indices 3 (this is the class of nucleotides C and G) and hydrogen index 2 (this is the class of nucleotides A and T) is the sum of two sparse matrices: 0.4172^[1, 0; 0, 1] + 0.5828^[0, 1; 1, 0]. The set of these two matrices e 0 = [1, 0; 0, 1] and e 1 = [0, 1; 1, 0] is closed under multiplication and corresponds to the multiplication table of basic elements of the algebra of 2-dimensional hyperbolic numbers [32]. Thus, this 2-bit Karnaugh matrix in the considered example of DNA of the human chromosome № 1 is a matrix representation of the 2dimensional hyperbolic number 0.4172e 0 + 0.5828e 1 . For other genomic DNAs, the corresponding 2-dimensional hyperbolic number will have other coordinates and different genomic DNAs can be compared by these hyperbolic numbers.

The 4-bit Karnaugh matrix for four equivalence classes of nucleotides with hydrogen indices 33, 32, 22, 23 is the sum of four sparse matrices:

0.1626∙[1,0,0,0; 0,1,0,0; 0,0,1,0; 0,0,0,1] + 0.2546∙[0,1,0,0; 1,0,0,0,0; 0,0,0,1; 0,0,1,0] + +0.3281∙[0,0,1,0; 0,0,0,1; 1,0,0,0; 0,1,0,0] + 0.2546∙[0,0,0,1; 0,0,1,0; 0,1,0,0; 1,0,0,0]. (6)

The four sparse matrices, shown in parentheses in (5), form a multiplication-closed set of matrices defining the multiplication table of the basic elements of the algebra of 4-dimensional hyperbolic numbers. Thus, this 4-bit Karnaugh matrix in the considered example of DNA of the human chromosome № 1 is a matrix representation of a 4-dimensional hyperbolic number. For other genomic DNAs, the corresponding 4-dimensional hyperbolic number will have different coordinates.

Similarly, the 3-bit Karnaugh matrix of probabilities of hydrogen equivalence classes (Fig. 4) is related to the algebra of 8-dimensional hyperbolic numbers and is a matrix representation of an 8-dimensional hyperbolic number. These algebraic facts further confirm the connection of the genetic coding system and genetic informatics with cyclic n-bit Gray codes, n-bit Karnaugh matrices, and functions of the Boolean algebra of logic (let me repeat that analogs of these Karnaugh matrices with the numbering of their columns and rows by Gray codes have long been used in applications of the Boolean algebra of logic).

The fact of conjugation of genetic Karnaugh matrices of hydrogen equivalence classes in genomic DNAs with algebras of 2ⁿ-dimensional hyperbolic numbers is important, in particular, because they are related to the hyperbolic geometry of Lobachevsky, which is actively used in deep neural networks of artificial intelligence [36]. Many biological phenomena are also related to hyperbolic geometry and hyperbolic rotations [34-36]. In particular, the basic psychophysical Weber-Fechner law, which governs all types of our sensory perception of the world - visual, auditory, olfactory, tactile, gustatory, etc. -, is also related to hyperbolic geometry [34, 35]. Significantly, the genetically inherited Weber-Fechner law is a law not only of the nervous system. It is also valid for lower organisms that do not have nerve cells: “ This law applies to chemo-tropical, helio-tropical and geo-tropical movements of bacteria, fungi, and antherozoids of ferns, mosses, and phanerogams... The Weber-Fechner law, therefore, is not the law of the nervous system and its centers, but the law of protoplasm in general and its ability to respond to stimuli ” [37, p. 126]. Note that the Weber-Fechner law, in essence, pertains to the topic of gestalt archetypes of probabilities, since in living bodies all processes are essentially stochastic-deterministic and since the most diverse sensory flows of biological information (visual, auditory, tactile, olfactory, etc.) are represented by this general archetypal law, genetically transmitted from generation to generation.

The genetic Karnaugh matrices of genomic probabilities of n-plets (like those shown in Fig. 4) are bisymmetric with real values and therefore have real eigenvalues, eigenvectors, and characteristic polynomials. These polynomials of the genetic Karnaugh matrices of probabilities bring algebraic genetics closer to algebraic geometry, one of the central branches of mathematics, and focuses on polynomial functions. From the presented point of view, the statistical organization of the binary sequence of strong and weak hydrogen bonds of DNA of any genomes and genes can be additionally characterized by the corresponding family of characteristic polynomials of (2n×2n) probability matrices for comparative analysis of different DNAs, as well as for identifying information patents of living nature in the field of genetics.

Identifying universal rules of stochastic-deterministic organization of sequences of hydrogen bonds 2 and 3 in genomic DNAs provides additional grounds for increased interest in hydrogen medicine, which has been intensively developed in many countries since 2007 [38]. Work on hydrogen medicine can be supplemented with the use of bioactivating acoustic and vibration effects in medicine, plant growth, and veterinary science. To date, among more than 1000 publications worldwide on the impact of hydrogen on the human body, there is not a single one about its harmful or side effects. Here it can be recalled that up to 12 liters of gaseous hydrogen are produced daily in the human intestine.

The nucleus of the most common hydrogen isotope, protium, consists of only one proton. There is evidence of the important role of protons in the numerical and functional characteristics of the genetic coding system, associated with a specific "bio-arithmetic of protons" and presented in the works [18, 19]. The author believes that biomolecular structured sets of protons determine much of the genetic inheritance of cyclic ensembles in living bodies. The above-described genetic Karnaugh matrices and cyclic Gray codes are now used to analyze this problem.

• 4.3.    Multidimensional Gray Codes and Karnaugh "Chessboard" Matrices

Along with the one-dimensional Gray codes described in Appendix 1, there are multidimensional Gray codes, primarily 2D- and 3D-Gray codes. In technologies, they are used, for example, in quadrature amplitude modulation, which is applied to transmit color signals in the PAL and NTSC television standards, in stereophonic radio broadcasting (AM stereo), in software-defined radio (SDR) systems [39, 40]. In a 2D-Gray code, the Hamming distance between adjacent terms (code words) is 2 (but not 1 as in the 1D-Gray code). Accordingly, in a 3D-Gray code, the Hamming distance between adjacent terms is 3.

The 2D-Gray code splits the sequence of members of the 1D Gray code into two halves, one of which contains even terms (in decimal equivalents) and the other contains odd terms. This can be associated with the problem of the “oddeven” numbers in the long-standing topic of the difference in the functions of the two inherited hemispheres of the brain, as well as the “odd-even” binary of the basic codes of human culture and dialogue theory [25]. For example, the sequence of the 3-bit 1D-Gray code 000, 001, 011, 010, 110, 111, 101, 100 is split by the 2D-Gray code into two cyclic subsequences, between the terms in each of which the Hamming distance is 2: more precisely, the subsequence of even numbers 000, 011, 110, 101 and the subsequence of odd numbers 001, 010, 111, 100.

In genetic n-bit Karnaugh matrices (Fig. 1), adjacent cells with a Hamming distance of 2 between them are located diagonally. Accordingly, the n-bit 2D-Gray code divides the entire set of cells of the n-bit Karnaugh matrices into two subsets with even and odd numberings, which is reflected in the diagonal mosaic of black and white cells representing these numerical subsets (Fig. 1). Note that in the case of the genetic vertebrate mitochondria code, which is considered the most ancient and symmetrical among all dialects of the genetic code, the entire natural set of amino acids and stopcodons in black-and-white Karnaugh matrices for triplets is structured in a very regular way: this set is divided into two subsets of absolutely identical composition, one of which occupies all the black cells, i.e. cells with even numbers according to the 6-bit Gray code, and the second of which occupies all the white cells, i.e. cells with odd numbers of the 6-bit Gray code (see [2, Fig. 2.2]). Note also that cyclic shifts in the numberings by Gray codes (i.e. cyclic shifts of bits in the corresponding Gray codes) of the columns and rows of these Karnaugh matrices in Fig. 1 change the arrangement of many n-plets in them, but the black-and-white mosaic of these matrices is conserved as invariant since the previous and new cells in the arrangement of each n-plet always have the same color (it is a feature of the migration of matrix cells within their color community under such cyclic shifts).

Genetically inherited locomotion of humans, many vertebrates, insects, centipedes, etc. corresponds to such a diagonal pattern (resembling the pattern of the 2D-Gray code on the genetic Karnaugh map) of alternating symmetrical left and right halves of their musculoskeletal system during locomotion. According to the author, Karnaugh matrices can be used for algebraic modeling of these algorithmically organized and genetically inherited locomotor movements within the framework of cyclic genetic biomechanics.

The black-and-white mosaic of genetic Karnaugh matrices that arises from the algorithms of n-bit 2D-Gray codes resembles the diagonal mosaic of a chessboard, which has been used since ancient times in checkers and chess, popular all over the world. In this regard, we consider a chessboard with its 64 cells as an overlay on a genetic 3-bit Karnaugh matrix for 64 triplets (Fig. 1), which can be its genetic prototype and have structural connections with the algorithmic rules of moves in checkers and chess.

In this case, each square of the chessboard receives a corresponding number from the 6-bit Gray code (this numbering of all 64 squares is shown in Fig. 1). Then, in checkers and chess, the algorithmic moves of checkers and chess pieces appear as transitions between numbers (code words) of the 6-bit Gray code at the 3-bit Karnaugh matrix. In this case, the historically established algorithmic move of each checker to an adjacent square along the diagonal, used in checkers, corresponds to its transition to a square of the same color, the number of which differs from the Gray number of the original square by the Hamming distance of 2, that is, it is carried out according to the algorithm of the 2D-Gray code. A game similar to checkers was widespread in Ancient Egypt and the first mentions of it date back to 1600 BC, i.e. more than 3000 years ago; the ancient Egyptians believed that checkers were invented by the god of wisdom Thoth .

In chess, the algorithmic moves of all pawns and pieces (except the knight) specified by the rules can be represented as moves to adjacent cells along a straight line or diagonally corresponding to the algorithms of the 1D- and 2D-Gray codes (with possible multiple repetitions of moves in the case of chess rooks and bishops). And the moves of the chess knight turn out to correspond to the 3D-Gray code, since the knight’s move always takes it to a cell whose number, according to the 6-bit Gray code, differs by exactly three bits from a number of the original cell (that is, Hamming distance between them is 3). The routes of the knight on the chessboard have been the subject of the works of many mathematicians, starting at least in the 18th century. The most famous of these are the works of L. Euler [41] and his followers on the question of whether a knight can go around all 64 cells of a chessboard without stepping on any cell twice. By now it is known that such a knight’s route exists in many variations, but nowhere is the connection of the knight’s movements with Gray codes mentioned (as far as the author knows). The website provides examples of knight’s routes, including a cyclic type, in which the knight moves from the last cell #64 of the route to cell #1 of the route, which can be infinitely cyclically repeated. It is also indicated that there are more than 26 trillion (26,534,728,821,064) such cyclically closed routes. In addition, there are still unclosed routes, i.e. those in which it is impossible to move the knight from cell #64 to cell #1. From a mathematical point of view, in our opinion, it is interesting to continue studying these unclosed knight’s routes on extended chess-like genetic n-bit Karnaugh matrices for n = 4, 5, etc. (with their size 16x16, 32x32, …).

Thus, a connection has been discovered between the algorithmic organization of chess and checkers and genetic Karnaugh matrices, cyclic Gray codes, and the theme of the cyclic nature of living organisms. In particular, this connection is interesting in light of historical data on the significance of the images of a chessboard and 64 cells of the Vastu Mandala in ancient Indian philosophy; the Agni-Purana speaks of a plan of 64 cells as a mystical diagram of the Vedas, a model of the world . It is not without reason that India is considered the birthplace of chess. The discovered connection testifies in favor of the genetic archetypal nature of the attraction of people to chess and checkers, as well as the genetic basis of several ideas in ancient Indian philosophy.

But the 3-bit Karnaugh matrix for 64 triplets is associated not only with the algorithms of moves in checkers and chess but also with the amino acids that are encoded by these triplets (Fig. 1). This allows us to formally match the routes of checkers and chess pieces (including the chess knight) with amino acid sequences in proteins, etc. For example, a particular route of a knight on such a genetic board corresponds to a certain sequence of n-plets and amino acids, which can be matched with real sequences of n-plets in genomes and genes, as well as amino acid sequences in proteins. In this case, each cell of the board has a certain probability of the corresponding triplet in the considered DNA of the genome. Therefore, it is possible to build selective routes of the knight based on the principle of, for example, the next move of the knight to the cell with the maximum (or minimum) probability. For different genomes, there may be various routes of the knight, since the probabilities of triplets in the DNA of different genomes are different. Stop-codon cells in this sequence of moves may not be taken into account, since they do not encode amino acids. Could there be benefits from developing such a kind of "chess genetics", in which genetic sequences are matched to the algorithmic paths of checkers and chess pieces? This is a question for future study.

5. Some Concluding Remarks

One can assume that the universal rules of genomic DNAs, revealed by the author, are connected with the quantum and physical mechanisms of oscillatory (vibrational and cyclic) interaction of components in huge inherited ensembles of vibrational and cyclic processes of living matter. These mechanisms should be studied by science. No wonder the structural organization of the genetic coding system is associated with matrix formalisms of the theory of resonances of oscillatory systems with many degrees of freedom, which is reflected in the concept of poly-resonance genetics [34]. Resonance interactions have long been considered in science as one of the key mechanisms of self-organization. The theme of oscillatory processes in living bodies is extensive. For example, progress in the microphone measurement technique made it possible to establish that individual body cells vibrate, making sounds in the acoustic range, which served as the development of the scientific direction of “sonocytology” [42].

As noted above, processes in living bodies are largely stochastic, since already in the cell the interactions of molecules are stochastic. Even genetically identical cells in one tissue have different levels of protein expression, sizes, and structure due to the stochastic nature of the energy interaction of individual molecules in cells. The stochastic nature of the inheritance of traits in the “small regions” is radically different from the deterministic inheritance of the traits in the “large regions” (the topic of gestalt-biology). For example, prints of the fingertips of all people are different even though the fingers in the “whole” are practically determined in shape and structure (3 phalanxes, etc.). Thus, biological phenomena are associated with fundamental dualism "stochastics-and-determinism". According to the law of Mendel of independent inheritance of traits, information from the level of DNA molecules dictates the macrostructure of living bodies on many independent channels despite severe noises. For example, the colors of the hair, eyes, and skin are inherited independently of each other. Accordingly, each organism is a machine of multi-channel noise-resistant coding. The author believes that the future of biology is associated with the study of the deep and logical system of segregated genetic probabilities.

The numerous dichotomic fractal trees of probabilities, described in this article about the statistical organization of genomic DNAs, resemble the well-known dichotomic and fractal structures in configurations of living bodies. But in genomic DNAs, unlike morphological structures, we meet fundamentally another type of dichotomies: dichotomies of statistical (probabilistic) characteristics in the information sequences of DNA. Extensive dichotomic fractal networks of genomic DNA probabilities are the soil from which living bodies and genetic intelligence grow. The morphological structures of living bodies do not arise from scratch, but, as one can think, have structural prototypes in the logical system of genomic gestalt-archetypes of probabilities, the examples of which are presented in this article.

As noted above, our brain, containing 86 billion nerve cells and one quadrillion interneuronal contacts, operates on probabilistic principles, since the transmission of each impulse from neuron to neuron can be influenced by an immense number of factors (tens of types of neurotransmitters, etc.). But based on statistical information from the flows of neural impulses in the brain, we obtain a deterministic holistic (gestalt) representation of specific objects in the surrounding world. Uncovering the secrets of this relationship between stochastics and determinism in living things is a fundamental task of science. Since the brain is inherited through the system of genetic coding, it can be assumed that by learning universal gestalt archetypes of genomic probabilities in genetics using algebraic and algebraic-logical methods, we also indirectly learn the probabilistic principles of brain operation, the algorithms of quantum bioinformatics, and the possible foundations of genomorphic systems of artificial intelligence. The presented results indicate that the implementation of inherited gestalt-archetypes of probabilities in genetics and physiology is structurally connected with cyclic Gray codes, genetic Karnaugh matrices, and inherited sets of coordinated cyclic bioprocesses.

The rules of gestalt archetypes of genomic probabilities described in the article were revealed using the effective author's method of "hierarchies of multilayered statistics", according to which the textual sequence of any genomic DNA is represented as a regular multilayered configuration of a set of n-plet texts. This textual multilayeredness of genomic DNAs can be associated with multilayeredness in the embryology of multicellular organisms. We are talking about germ layers, that is, layers of the body of the embryo of multicellular organisms formed in the process of gastrulation and giving rise to various organs and tissues [43]. In all animals, homologous organs are obtained from the same germ layer. An important conclusion follows: in all animals, the main organ systems have a common origin and can be compared. Germ layers are one of the pieces of evidence of the common origin and unity of the entire animal world. Note that after fertilization the egg cell is successively divided into 2, 4, 8, 16 cells, etc., which corresponds to the number 2n members in n-bit Gray codes. These data support the idea that the regular holistic organization of genetically inherited morphological configurations (morphogenesis gestalts) is realized through multilayered structures, examples of which in the multilayered stochastic-deterministic organization of genomic DNAs are described above.

The genetic system's regularities are actively used worldwide in mechanical engineering and other fields of science and technology in connection with the so-called genetic algorithms [44-46]. Many monographs, articles, conferences, hundreds of patents, etc. are devoted to genetic algorithms of search and optimization that imitate natural genetic processes using fitness functions. They are used in very different problems from the design of space antennas and bridges to computer programming, artificial intelligence problems, protein structure recognition, and financial forecasting. In genetic algorithms, in particular, Gray codes are used [47]. The above-presented rules of gestalt-archetypes of probabilities in the multilayer stochastic-deterministic organization of genomic DNAs, associated with Gray codes and genetic Karnaugh matrices, can be used to introduce new types of fitness functions to create, based on such algorithms, multilayer structures, in which statistical characteristics and holistic images (gestalts) in different layers will be related to each other according to the genomic DNA rules found.

The genomic gestalt archetypes, presented in this article, can be compared with the well-known teaching of the founder of analytical psychology, C. Jung, about the human archetypes of the collective unconscious [48, 49]. Jung developed this teaching in connection with his psychological studies of consciousness in people without reference to any mathematical formalisms and structures of the genetic coding system. The learning developed by the author of this article about the genomic gestalt-archetypes of probabilities related to all organisms and their genetically inherited physiological characteristics (and not only to humans and their consciousness) has the following main differences from Jung's teaching: 1) it is based on data on the lawful statistical organization of the genomic DNA of higher and lower organisms; 2) it is algebraic since it is based on the algebraic formalisms of cyclic Gray codes, genetic Karnaugh matrices, Boolean logic algebra, Walsh-Hadamard functions, fractal Hilbert curves, dichotomous fractal trees, and tensor-unitary transformations [50]. One can think that some of the archetypes of the collective unconscious in people are consequences or appearance of general biological genomic archetypes. These studies are ongoing.

As was shown at the beginning of the article, the binary opposition characteristics of 4 nucleotides C, A, T, and G, giving the numerical representations C = T = 0, A = G= 1 and C = A = 0, T = G = 1, were used in genetic (2n∙2n)-Karnaugh matrices (Fig. 1) when numbering their columns and rows in the order of members of n-bit Gray codes. But these same numerical representations can be used for numbering the columns and rows of genetic (2n∙2n)-matrices in a different order, namely, in the order of members of dyadic groups of n-bit binary numbers (for example, the sequence of numbers in a dyadic group of 3-bit binary numbers is: 000, 001, 010, 011, 100, 101, 110, 111). In this case, instead of the family of genetic Karnaugh matrices (Fig. 1), a tensor family of genetic (2n∙2n)-matrices automatically arises, the members of which are interconnected by the tensor (Kronecker) product of matrices, which was previously described by the author in books [18, 19, 21]. Thus, genetic n-bit Karnaugh matrices turn out to be indirectly connected with the tensor product of matrices, which plays an important role in quantum information science [26]. The n-plet compositions of columns, rows, and quadrants in the genetic matrices of the tensorial family and the corresponding genetic Karnaugh matrices are similar up to a permutation of some n-plets. In this case, the mentioned permutation of n-plets is such that for the columns, rows, and quadrants of the matrices of the tensorial family, genomic gestalt-archetypes of total probabilities are also fulfilled by analogy the genomic gestalt-archetypes of the family of genetic Karnaugh matrices presented above. It can also be emphasized that the genetic matrices of the tensor family have deep analogies with the tables of the ancient Chinese "Book of Cyclic Changes" (I-Ching), as noted by the author in the works [18, 19].

Appendix 1. On Cyclic Gray Codes

The Gray code is cyclic since cyclic shifts of each code word yield another word that belongs to it [51-53]. Gray codes find application in all areas of mathematics where there is a need for a quick enumeration of all subsets [54]. Gray codes for four or more bits are not unique and even allow for a permutation or inversion of bits. The most typical type of Gray code used in digital systems is the symmetrically reflected Gray code. This name is associated with the following algorithm for constructing a hierarchy of such reflected n-bit Gray codes. Let Gn be a sequence of terms of an n-bit Gray code, and let the sequence GnR have an order inverse to the order of the sequence Gn. Then the sequence Gn+1 of the reflected (n+1)-bit Gray code is obtained by assigning the symbol 0 from the left to each term of the sequence Gn and the symbol 1 from the left to each term of the sequence GnR and combining them in the final step. For example, for n = 2, we have Gn: 00, 01, 11, 10; GnR: 10, 11, 01, 00. After the specified assignment of 0 on the left to the members of Gn and 1 on the left to the members of GnR, we obtain 3-bit sequences 000, 001, 011, 010 and 110, 111, 101, 100. Rewriting these two sequences one after the other, we receive the reflected 3-bit Gray code G3: 000, 001, 011, 010, 110, 111, 101, 100. If we ignore the first bit in the members of the resulting 3-bit Gray code, then its left and right halves are mirror-symmetrical. There is an online calculator of reflected n-bit Gray codes up to n=16 on the Internet . Any n-bit Gray code corresponds to a Hamiltonian cycle on an n-dimensional hypercube.

Gray codes are widely used in engineering technologies: rotary and optical encoders, including the encoding of track numbers on computer hard disks; error detection systems; Karnaugh maps, which are associated with Boolean functions and logical operations; the theory of genetic algorithms, etc. Many literary sources and Internet sites are devoted to Gray codes and their applications.

In this paper, we regard Gray codes in the wide sense as sequences of n-bit codewords (or binary strings) in which any two adjacent codewords differ by exactly one-bit position, including the same difference between its last and first codewords, which are interpreted as adjacent codewords (the Hamming distance between them is 1). In this approach, cyclic sequences in Gray codes can often be viewed as hypercycles containing cyclic subsequences of Gray codewords (or truncated cyclic Gray codes) within them. For example, the 3-bit Gray code 000, 001, 011, 010, 110, 111, 101, 100 contains cyclic subsequences, each of which can be viewed as a cyclic Gray code in the wide sense:

• •    any pair of adjacent codewords in this cyclic sequence of 8 codewords is a separate cyclic subsequence (e.g., 000, 001, or 010, 110);

• •    the first four codewords (000, 001, 011, 010) are a cyclic subsequence with unit Hamming distance between adjacent terms. The same is true for the subsequence of the last four codewords (110, 111, 101, 100);

• •    symmetrical cutting of the same number of code words from both ends of the Gray code sequence generates a cyclic subsequence (for example, by removing one term from both ends of the sequence under consideration, we obtain the cyclic subsequence 001, 011, 010, 110, 111, 101, and by removing 2 terms from both ends, we obtain another cyclic subsequence 011, 010, 110, 111). Each of these subsequences, being a cyclic Gray code in the extended sense, can serve as a basis for the formation of Gray codes of increased bit capacity using the algorithm for constructing a symmetrically reflected Gray code described above. For example, using this algorithm, a cyclic subsequence of 3-bit codewords 000, 001 generates a cyclic sequence of 4-bit codewords 0000, 0001, 1001, 1000, which creates, using the same algorithm, a cyclic sequence of 5-bit code words. 00000, 00001, 01001, 01000, 11000, 11001, 10001, 10000 and so on. This property of cyclic Gray codes, considered in a broad sense, can be called the property of regeneration of multi-bit families of Gray codes from truncated (fragmented) Gray codes. The property of regeneration of families of Gray codes evokes associations with the well-known regenerative and holographic properties of living organisms, described, for example, in [55, 56]. For example, as is known in embryology, by separating the blastomeres of sea urchin eggs from each other, normal (albeit reduced) larvae with all their organs can be grown from one embryonic cell (blastomere). Similar bio-holographic phenomena of distributed information have been repeatedly confirmed by biologists in many taxonomic groups of multicellular organisms - from sponges to mammals.

Acknowledgments

The author is grateful to A.A. Koblyakov, S.Ya. Kotkovsky, Yu.I. Manin, M.M. Puchkov, E.G. Rajan, V. Rosenfeld, V.I. Svirin, I.S. Soshinsky, I.V. Stepanyan, G.K. Tolokonnikov, E. Fimmel, V.I. Chernoivanov, S.V. Shushardzhan, M. He, and Z.B. Hu for discussion of the results and cooperation.