Алгоритм анализа тонкого электрического вибратора

1. Распределение тока по вибратору

Рассмотрим симметричный вибратор. Будем исходить из интегрального уравнения Халлена [1].

N

I z ( z ) = £ I n f ( z ), n = 1

l

J I z ( z ') G ( z - z ') dz' =

- 1

C cos kz - ^n^ sin k | z |,

где I_z ( z ') — неизвестное распределение тока; C — неизвестная постоянная; U – напряжение в зазоре вибратора; G ( z - z ') — функция Грина:

G ( z - z ') =

- ikR e

R

exp ( - ik^j ( z - z ')² + a ² )

V( z - z ')² + aa

где I_n – коэффициенты разложения, подлежащие определению. Функции f_n ( z ) называются базисными; они должны быть линейно независимы. В случае точного решения уравнения Халлена они должны составлять полную систему функций и суммирование в (2) должно быть бесконечным. Удобно функции f_n ( z ) выбирать так, чтобы удовлетворялись граничные условия для тока на концах вибратора, т. е.

f n (± l ) = 0 .

Существует много методов решения интегрального уравнения Халлена; рассмотрим один из них. Решение уравнения (1) можно представить в виде разложения искомой функции в ряд по некоторой системе функций f ₁( z ), f ₂( z ), f ₃( z ), … :

Для сравнительно коротких вибраторов, представляющих наибольший практический интерес, оказывается достаточным с инженерной точки зрения ограничиваться несколькими членами ряда (2). Подставляя (2) в уравнение (1),

получим

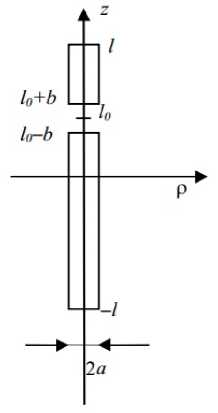
Рис. 1. Геометрия вибратора

l

^ I n J f n ( z ‘) G ( z - z ‘) dz' = n - l

= C cos kz - ^^Л^ sin k | z | .

Z

Для решения уравнения (3) относительно неизвестных коэффициентов I_n необходимо свести его к системе линейных алгебраических уравнений. Это можно сделать, например, методом согласования в точках. Для этой цели умножим левую и правую часть уравнения (3) на дельтафункции 5( z - z p ), где p = 1, 2, 3, ^ — номера точек разбиения интервала - 1 ^ l на отрезки. Затем проинтегрируем полученное выражение по z от - 1 до l и получим следующую систему уравнений:

l

У I n J f n ( z ') G ( Z p - z ') dz ‘ = n - 1

= C cos kz p

-

i 2n U

Z

sin k | z_p

Рассмотрим случай, когда вибратор находится в вакууме. С учетом того, что k = k o = 2п / X, Z = Z o = 120п, перейдем в уравнениях (5) к безразмерным величинам t ‘ = z' / l , t = z / l:

p = 1, N .

Таким образом, интегральное уравнение Хал-лена (1) сведено к системе линейных алгебраических уравнений относительно неизвестных постоянных I n ( n = 1, N ). Переход от (1) к (4) означает, что интегральное уравнение Халле на (1) удовлетворяется только в N точках Z p ( p = 1, N ).

Для коротких вибраторов оказывается удобным выбирать базисные функции в виде простых степенных выражений:

n fn (z) = 11 - I ; n = 1- N,

N

EI F (t ) - C cos 2n xt = nn p         p n=1

i 2n U

-

Z 0

sin 2n x | t p

|,

где

t p = ( p -1) - N -; p = 1,2,3, - N + 1,

Fn (t) = l            exp (-i2л5(t - t')2 + y2 )

= J (1- 1 1' ^b n ----- /      , 2     2         dt ^

- 1                 tt ^- t ) ⁺ y

5 = l / X, y = a / 1 .

и, следовательно, представить разложение (2) в

Выражение (6) перепишем в следующем виде:

виде полиномов.

Поскольку в уравнениях (4) содержится неизвестная постоянная C , порядок системы этих уравнений должен быть на единицу больше порядка полинома N . Таким образом, задача сводится к решению на ПЭВМ следующей системы линейных алгебраических уравнений:

N

У InFn(zp) - C cos kzp = n=1

N

I z ( t ) = ^ I n (1-| t |) n .

n = 1

2. Определение диаграммы направленности вибратора

Нормированная характеристика направленности имеет вид:

F ₆ (6, Ф) =

i 2n U

= - — sin k | z p |;                             (5)

p = 1,2,3 ... N + 1;

где

E ₆ О, Ф)

| E 6 max ⁽⁶, ^ф) |

l

F n

( ^{z )}= J

- l

-

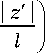
exp ( - ik J ( z - z ')² + a ² ) ------dz '.

( z - z ')² + a ²

Зная распределения тока вдоль вибратора, можно найти составляющую поля E 6 :

iZ 5 exp (- ikR )

E 6 =--;

2 r

N l(9)

х У In J (1- 1 1' |) ⁿexp ( i 2n5 1' cos 6) dt '.

n=1

Значения функции F_n ( z ) можно найти методами численного интегрирования.

Выбор координат точек разбиения zp удобно производить по правилу zp = (p - 1)N p = 1,2,3,...N + 1

и определять, таким образом, в (5) значения коэффициентов только по точкам z_p одного плеча вибратора. Для симметричного вибратора этого вполне достаточно. После определения коэффициентов I_n находится распределение токов в вибраторе по формуле

Nn

L (z) = У L, | 1 - I . zn n=1   ^ z

На рис. 1 показаны: l – длина половины вибратора; a - радиус провода; 5 = l / X — отношение половины длины вибратора к длине волны.

3. Пример численного расчета тонкого электрического вибратора

Все вычисления и построения произведены в системе MathCad 15 для следующих параметров: 5 = l / X = 7/10, y = a / 1 = 1/ 400.

В качестве аппроксимации функции (6), описывающей распределение тока по вибратору, использовался полином 5-го порядка. Для определения коэффициентов I_n необходимо решить систему из 6 линейных уравнений:

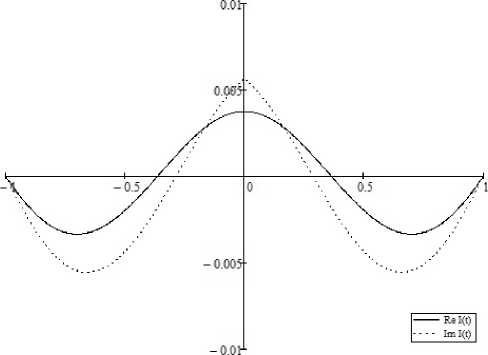
Рис. 2. Распределение тока вдоль вибратора с параметрами l / X = 7/10, a / l = 1/400

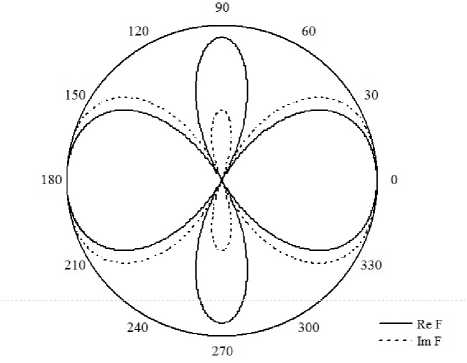
Рис. 3. Нормированная характеристика направленности с параметрами l / X = 7/10, a / l = 1/ 400

EbF (t„) - C cos2n51„ = nn pp n=1

_ — г2л17 sin2n§ |t |.(10)

Z0

P = 1,6, где tp = (p - 1) / 5. Систему алгебраических уравнений (10) будем решать методом LU-разложения (функция lsolve).

Вычисляем коэффициенты I_n для параметров 5 = l / X = 7/10, y = a / l = 1/400:

I 1 = -0.02 - i 0.027;

• 1 ₂    = 0.017 + i 6.821 ■ 10 ^{- 3};

• 1 ₃    = 0.068 + i 0.112;

• 1 ₄    = -0.087 - i 0.118;

• 1 ₅    = 0.026 + i 0.032.

Подставив найденные коэффициенты в формулу (7), построим графики распределения тока вдоль вибратора (рис. 2). Сп л ошной л инией показана действительная часть тока, а штриховой – мнимая часть составляющей.

Подставляя эти коэффициенты в (9), определяем зависимость компоненты поля E g от угла 9. Подставляя эти значения в (8), находим нормированную характеристику направленности вибратора (рис. 3).