Алгоритм быстрого построения дескрипторов изображения, основанных на технике гистограмм ориентированных градиентов

Описание изображения является промежуточным, но крайне важным этапом решения задач компьютерного зрения. В процессе описания изображения производится преобразование визуальных данных, содержащихся на. изображении, в приемлемую для алгоритма, классификации форму.

Так как в визуальных данных обычно содержится много излишней информации, то задача описания помимо прочего состоит в исключении как можно большего количества неинформативных признаков при сохранении данных обо всех существенных для задачи распознавания характеристиках исследуемого фрагмента, изображения.

В данной статье исследуется описание изображений в задаче распознавания, и представлена реализация быстрого алгоритма построения класса дескрипторов, основанных на технике гистограмм ориентированных градиентов (HOG - histogram of oriented gradients).

HOG дескрипторы используются классификаторами SVM, Random Forest, Boosting и многими другими.

2.    Гистограмма ориентированных градиентов

В основе данного метода, лежит предположение, что вид распределения градиентов интенсивности изображения позволяет достаточно точно определить наличие и форму присутствующих на нем объектов.

При описании фрагмента, изображения оно разбивается на. несколько небольших участков, далее называемых ячейками. В ячейках вычисляются гистограммы h направленных градиентов внутренних точек. Обычно они объединяются в одну гистограмму һ = / (hi,..., һ^ ), после чего она нормализуется по яркости (L2 ил и Li норма):

^һь2 = _х, ^hL1 = іһТ+^, = ^¹

где е — некоторая малая константа.

Рис. 1. Скользящее окно

Таким образом, данный описатель содержит пространственную информацию о фрагменте и инвариантен к освещению.

При вычислении градиентов производится свертка изображения с ядрами [—1, 0,1] и [—1, 0,1]^т, в результате чего образуются две матрицы D_x и Dy производных вдоль осей ж и у соответственно. Эти матрицы используются для вычисления углов и величин (модулей) градиентов в каждой точке изображения.

Пусть множество углов (—тг,тг] разбивается на п равных интервалов вида ( — ^-¹ тг, ^тг], где к = {1,...,п}. Каждому интервалу ставится в соответствие бин гистограммы. Тогда гистограмма, ячейки заполняется так, что величина, градиента, в каждой внутренней его точке добавляется к величине бина, соответсвующего интервалу, содержащему угол данного градиента.

Обычно ячейки, так же, как и сами фрагменты, имеют прямоугольную форму (рис. 1), которая позволяет применять технику интегральных изображений.

3.    Вспомогательные техники

Алгоритм построения дескрипторов удобно рассматривать как систему, состоящую из нескольких вспомогательных техник:

• 1)    интегральное представление изображений;

• 2)    интегральные градиенты;

• 3)    прореживание;

• 4)    имитация алгоритма, скольжения;

• 5)    вспомогательные дескрипторы.

3.1.    Интегральное представление изображений

Рассмотрим их более подробно.

Во многих задачах обработки изображений, таких как построение гистограмм ориентированных градиентов и фильтры Хаара, необходимо вычислять суммарную яркость прямоугольных участков изображения. Техника, интегральных изображений позволяет существенно ускорить данную операцию. При этом время вычисления суммы яркости прямоугольника. не зависит от его площади.

Пусть имеется отображение I из множества матриц R^mxn в R^(m+1)x(n+1)_j такое что

VX Е Rmxn

ЗУ _е R^(m+1)x(n+1), у = I ( X )

x - 1 ,y - 1

У (ж, у) = <

У^ X ( i,j ), при ж >  0 и у >  0;

0, при ж = 0 ил и у = 0.

Расчет матрицы У = I ( X ) занимает линейное время, пропорциональное числу пикселей в исходном изображении:

^у(ж,у) = ^X(ж - 1, у - 1) - ^{у (ж} - 1 ,у - 1) ^{+ у(ж,}у - 1) ^{+ у (ж} - 1, у^).

Время ее вычисления можно немного уменьшить, если сначала проинтегрировать столбцы матрицы X, а потом строки. При этом время вычисления интегрального изображения размером 500 х 500 уменьшается с 1, 242 мс до 1,108 мс.

По интегральной матрице (рис. 2) всего за 4 обращения можно вычислить сумму интенсивностей пикселей внутри произвольного прямоугольника ABCD исходного изображения X. Суммарная интенсивность в прямоугольнике ABCD вычисляется по формуле

S_x ( ABCD) = У ( Ax, A_y ) + У ( Cx, C_y ) - У ( Bx, B_y ) - У ( Dx , D_y ).

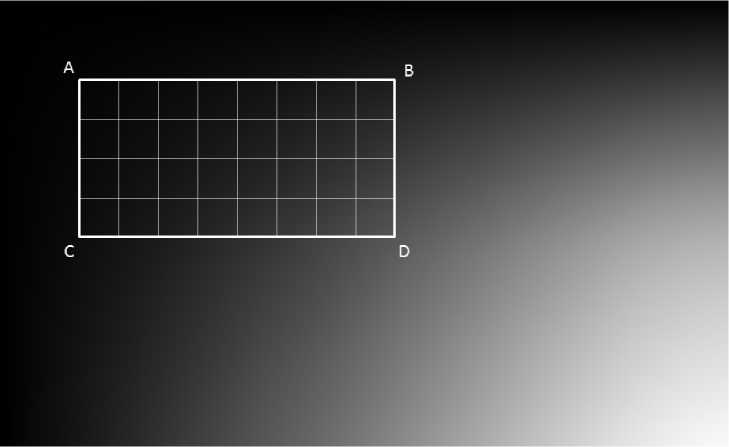
Рис. 2. Интегральное изображение

Более эффективно совершать подобное вычисление сразу для всего изображения. Пусть имеется матрица X Е R^mxn, тогда суммирование S_w^ изображения X по множеству всех прямоугольников размером w х Һ задается следующим образом:

VX Е R ^mxn А Е R ^(m-«⁺¹W-h⁺¹\ z = s_wh ( X ) :

Z (ж,у) =У (ж + w,y + Һ) + У (ж,у) - У (ж,у + Һ) - У (ж + w,y), где У = I(X), ж Е {0,..., m - w}, у Е {0,..., п - Һ}.

В статье техника интегральных изображений используется для построения интегральных градиентов изображения, с помощью которых вычисляются HOG дескрипторы.

3.2.    Интегральные градиенты

Пусть имеется две разностные матрицы D_x вдоль осей ж и у соответственно:

и Dy исходного изображения X € R^mxn

D_x ( ж,у' ) = X(ж, у) - X(ж + 1,у),ж € {0,... ,т - 1}, у € {0, ...,п},

Dy (ж, у ) = X ( ж,у) - X (ж, у + 1), ж € {0,..., т}, у € {0,..., п - 1}.

С их помощью вычисляются матрицы углов И и модулей V градиентов:

П(ж, у) = arctan

Д^у)

Dy (ж,у)

V (ж,у) = V D^(ж,у)2 + Dy (ж,у)2,

где ж € {0,..., т - 1}, у € {0,..., п - 1}.

Для построения гистограммы из п бинов эти матрицы приводятся к дискретному виду:

п ,

Аг^у) = [Дуу^],

^(ж,у) =

( V(ж,у), если Пп(ж,у) = г; | 0, если Пп(ж,у) = г, где п — количество бинов, г = {0,..., п-1}, [ж] — целая часть ж. Тогда бинами интегральных градиентов изображения B(X) будет называться множество матриц I(V).

Экспериментально было выявлено [1], что оптимальное качество распознавания достигается при количестве бинов порядка, восьми.

3.3.    Прореживание

Вычисление дескрипторов осуществляется в процессе сканирования изображения на. разных масштабах некоторым скользящим окном U (рис. 1). Пусть U = ( U_x,Uy ) - его текущие размеры, dU = ( dU_x,dUy ) - шаг скольжения, V = (Vc, V/) - размер ячеек, из которых оно состоит, a dV = (dV^, dVy ) - расстояние между ними.

Введем также понятие единицы длины Е = ( Е_х,Еу ), как вектор наибольшей длины, которому кратны векторы U, dU, V и dV. При Е = (1,1), не влияя на окончательный результат, интегральное изображение может быть прорежено так, чтобы новая единица, длины стала равна единичному вектору. Прореженная матрица Т (У) интегрального изображения У = I (X) вычисляется следующим образом:

уу € R(m+1)x(n+1) ЗУ € R(1+lm/E=:])x(1+[n/Ei' 1), У = Т(У) :

У(п,г) =У(n •Еу,г •Еу).

При прореживании все параметры скольжения сохраняют свои значения при всех масштабах скользящего окна, меняется только единица длины Е. При этом имеют постоянные dU значения отношения цу и "и ’ П0ЭТ0МУ качество распознавания инвариантно к размеру скользящего окна.

В статье прореживание применяется к бинам интегральных градиентов.

3.4.    Имитация алгоритма скольжения

Однотипные операции сразу со всеми элементами изображения, имеющими представление в виде числовой матрицы, поддаются оптимизации, поэтому скорость их выполнения может в несколько раз превосходить скорость поэлементного вычисления. Именно на. этом основана техника имитации алгоритма скольжения.

Пусть рабочая матрица X имеет размеры т хп. Тогда у скользящего окна U, размером w х Һ. имеется сопряженное скользящее окно U‘ (рис. 3). размером ( т -w + 1) х (п-Һ + 1).

Рис. 3. Сопряженное скользящее окно (зеленый прямоугольник). Клетка, в правом нижнем его углу соответствует извлекаемому элементу данных с координатами как в белом прямоугольнике

Таким образом, сканирование матрицы X скользящим окном U можно заменить сканированном окном U '.

Пусть шаг скольжения dU = (1,1), тогда сопряженное окно будет скользить с шагом dU ' = dV. Положение окна U ' может быть вычислено по формуле

U'Ди, г) = и • dU'х, U'у(и, г) = г • dU'у, где и G {0,..., [w/dU'ж]}, г G {0,..., [h/dU'у]}.

В каждом своем положении ( и, г) окно U ' покрывает некоторую подматрицу X_uu матрицы X:

Xu- (ж,у) = X (ж + U 'Ди, г), у + U 'у (и, г)), где ж G {0,..., m — w + 1}, у G {0,..., n — h + 1}.

Подматрица X_uu вытягивается в строчку и добавляется в матрицу искомых дескрипторов D.

Введем операцию R_mn перевода матрицы размера m х n в матрицу размером ( m + n) х 1, такую что

VX G R ^mxn ЗУ G R^(m+"^)x1,

У = Rmn(X ),У (и,г) = X (ж,у), где ж = и — у • m, у = [и/m], и = {0,..., (m + n) — 1}, г = 0. Тогда

DC^-W- + и )= Rmn ( Xuu ).

dU (£

Аналогично задается обратная операция Rmn:

Vy G R^(m+^n)x1 3X G R^mxn,

X = Rm1„(y),X (ж,у) = У (и, г), где и = ж + у • т,г = 0, ж = {0,..., m — 1}, у = {0,..., n — 1}.

Дескрипторы будут содержаться в столбцах матрицы D. При этом по номеру столбца можно однозначно определить размер и положение описываемого им фрагмента, изображения.

Пусть теперь dU = (1,1), тогда матрица X делится на dU_xdUy одинаковые части Xtj, размером ( m/dU_x) х ( n/dU_y ) каждая:

Xtj (ж, у) = X(ж • dUx + г,у • dUy + j )

где г = {0,..., dU_x — 1}, j = {0,..., dUy — 1}. Тогда окно U ' будет скользить по множеству матриц Xtj. Выбор матрицы из этого множества ( i,j ) зависит от положения окна (и, г):

г = (и • dV_x ) mod dU_x,j = (г • dV_y ) mod dU_y .

Остальные параметры скольжения изменятся следующим образом:

dU 'x = [dVx/dUx],dU 'у = [dVy/dUy ],w' = [w/dUx], h' = [h/dUy ],m' = [m/dUx],d = [n/dUy ].

3.5.    Вспомогательные дескрипторы

В более общем случае вычисление дескрипторов производится в несколько этапов скольжения. Пусть полученные на промежуточном этапе скольжения дескрипторы D преобразуются в матрицу D некоторым оператором F:

VD G R^(m+"^)x^ 3D' G R^(m+ⁿ)

^xh‘ , D' = F (D).

Из строк матрицы D' составляются матрицы D-, по которым совершается независимое скольжение:

D- G R^mxn, d - = B_m¹_n(D'(^, г)),г = {1,..., h'}.

Когда, все этапы скольжения пройдены, эти матрицы дескрипторов объединяются в одну итоговую матрицу.

4.    Конкретные описатели

Рассмотрим особенности реализации нескольких основных типов описания изображений, основанных на. технике гистограмм ориентированных градиентов.

4.1.    Характеристика SHOG

SHOG (simple histogram of oriented gradients) описатель является наиболее простым из HOG описателей. Если X - исходное изображение, то алгоритм его построения записывается следующим образом:

4.2.    Характеристика PHOG

Описатель PHOG (pyramid histogram of oriented gradients) [2] отличается от простого тем, что состоит из нескольких независимых этапов скольжения с разным размером ячеек V скользящего окна. Каждому размеру его ячеек соответствует так называемый уровень пирамиды. Обычно размеры ячеек на разных уровнях соотносятся как степень двойки:

V = U_x/2\ V = U_y/ 2 ^і,г = {0,..., L}, L < [log min ( U_x, U_y )].

Рассмотрим отдельно k-й уровень пирамиды. Вклад, который он внесет в квадрат модуля вектора дескриптора по отношению к нулевому уровню, составит величину порядка ^4=1 (4^-fc)² = 4^-fc. Чтобы вклад каждого уровня был одного порядка, необходимо умножить все элементы k-ro уровня на 2^к.

В силу резкого роста вычислительных затрат и падения важности элементов дескриптора с увеличением номера уровня пирамиды в большинстве прикладных задач имеет смысл использовать уровни не выше третьего.

4.3.    Характеристика OHOG

Описатель OHOG (original histogram of oriented gradients) был предложен в одной из первых статей [1], в которой изложена техника гистограмм ориентированных градиентов. В нем учитывается локальная зависимость нескольких соседних ячеек друг от друга. Иначе говоря, используется техника вспомогательных дескрипторов, которые нормируются по L2 норме.

4.4.    Характеристика GHOG

Можно объединить преимущества нескольких дескрипторов, например, OHOG и PHOG, создав из них композицию. В этом и состоит суть GHOG (general histogram of oriented gradients) описателя. Пусть d - GHOG дескриптор, d_i - PHOG дескриптор длины m, d2 ^ OHOG дескриптор длины n. Тогда

m

n        m+n

d = 2(dii,..

. , dim, d21, . . . , d2m), £ di, = 1, £ d2, = 1, £ d, = 1. i=i          i=ii=i

Аналогичным образом создаются композиции произвольного числа к нормированных на единицу дескрипторов:

Пі1

du = (d,i,...,dim),^dij = 1,d = —(dii,... ,dini,... ,dki,... ,dkrik). j=i

5.    Экспериментальные результаты

В вычислительном эксперименте тестовое изображение имело размер 1000x500, начальное значение единицы длины было равно 10 x 10, пропорции скользящего окна 4 x 4, шаг скольжения 1 x 1 (в единицах длины). В таблице 1 приведено потраченное на составление дескрипторов время. Результаты получены на процессоре Intel Core г7, 2.8 GHz. В случае многомасштабного скольжения с коэффициентом роста масштаба 1, 2 время скольжения увеличивается примерно в 3 раза.

Таблица!

Время построения дескрипторов всего изображения

Тип описателя	Параметры скольжения	Время скольжения (мс)	Время многомасштабного скольжения (мс)
SHOG	L = 3	23,7	66,2
PHOG	L = {1,2,3}	44,2	119,0
OHOG	C = 2 x 2,dC = 1 x 1	11,3	27,5
GHOG	L = {1, 2, 3}, V = 2 x 2,dV = 1 x 1	55,1	147,3

6.    Вывод

Таким образом, в работе был приведен алгоритм быстрого описания всего изображения, основанного на технике гистограмм ориентированных градиентов, инвариантного к геометрическим и фотометрическим искажениям, к степени освещенности и к размеру скользящего окна. При этом время построения дескрипторов — порядка 100 мс. Этой скорости вполне достаточно, чтобы использовать алгоритм как часть многих прикладных задач в распознавании образов и компьютерном зрении.