Алгоритм численного интегрирования на бесконечном интервале в задачах распространения электромагнитных импульсов

Численное интегрирование сложных функций на бесконечном интервале актуально и применяется в том случае, когда аналитическое вычисление невозможно. Проблема усложняется, если результатом расчетов должна быть функция, параметры которой описывают какой-либо физический процесс во времени или в пространстве. Классическим примером такой задачи является вычисление прямого и обратного преобразований Фурье, где результатом вычислений являются функции, связывающие временные и частотные описания физического процесса [1]. Известные численные методы вычисления несобственных интегралов имеют ряд недостатков, связанных с тем, что точность и скорость вычислений напрямую зависит от величины шага приращения и значений пределов интегрирования, которые при численных решениях всегда конечны. Невозможность получения конечной последовательности значений в общем случае не позволяет применить быстрое преобразование Фурье [2] для численного решения поставленной задачи.

Существующие методы численного вычисления несобственных интегралов требуют доработки. В частности, для точного и быстрого получения результата необходимо непрерывно оценивать текущее значение вычисляемой величины, на основе чего менять шаг приращений, и ограничить промежуток интегрирования, оценив получаемую погрешность.

Одной из таких задач, при решении которой эффективно применение рассматриваемого подхода, является анализ распространения импульсного электромагнитного сигнала в однородных поглощающих средах. В частности, процесс распространения по координате x прямоугольного электромагнитного импульса с амплитудой A и длительностью Д t описывается выражением, полученным на основе анализа работ [3, 4]:

1 м Д p ⁽ x ^, t )=^ П^Ле 2^я -M t

^j ( ⁽ t ^^{) to-} ( ^k X ⁽ ® ) - ^jk' x ⁽. ® ) ) x )

d r d to =

. м

=Are Я J

-м

,^{- k} X ^{( to );}

to

Ш1А1                      toAt sin ---- cos to-k (to)x--dto+ 2x2

. . м - k"(to): jA f e x ^{( )}

я ^J to

-м

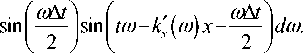
Здесь k X ( to ) и k'" ( to ) — параметры волнового вектора:

kX (to) =

k»=

^« ₀ to ( ² + e 2 s 2 to ² + 66 0 to

2      2 2 2

^ + e ^e ^ to ^L

ee ₀ to )

,

ц₀ = 1.256637-10 - ⁶ Гн/м, e ₀ = 8,85416Л0 - ¹² Ф/м, ст, м, e - удельная электрическая проводимость, относительные магнитная и диэлектрическая проницаемости среды соответственно.

В процессе распространения в поглощающей среде импульс изменяет свою форму и может появиться в точке пространства в определенный

момент времени, зависящей от скорости, определяемой свойствами среды. Целью расчетов является определение формы импульса в заданной точке среды в произвольный момент времени.

Рассмотрим вычисление действительной части выражения (1):

^kX ^{( m )} =

дд ₀ ® ( ² + e ² £ ^m + ee₀m

^

f. ⁽ t ⁾=I

—^

e—k X(m) x to sin

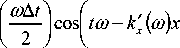
mN t ) , — I ^{d m} .(3)

^^ 0 ^7 ,m

Приближенное вычисление значения интеграла в выражении (3) осуществляется по методу трапеций. Обозначим подынтегральную функцию как:

Фх (t, m) = -

—

-k^{x ( m ) x} . л mN t )     (      ., г x     mN t )

------sin l-----I cos l t m — k ,( m ) x I m ( 2 Ik              2 I . (4)

Оценка значения функции (4) в точке to = 0 определяется через предел:

а            e ^{— kx m x} .(mN t )   Г , х    mN t )

Ф х ⁽ t ^{,0 )} = J im ® ^81П| “I ^Cos | t ® ^{— k}x ^{( m )} x27 I . (5)

Учитывая, что k X ( 0 ) = 0 и k X " ( 0 ) = 0 , выражение (5) приводится к виду:

a ( e0 . mN t фх (t ,0) = lim —sin----cos0

^xV’     m ^ 0

k

I

A t

₂ . (6)

Таким образом, приближенно интеграл (1) вычисляется по формуле:

fx (t ) "

Г.        ПЦ,                       ^

Фx (t,0) + Е(Фх (t, iNm) + Фх (t,—i Am)) — i=1

Фх (t, nА®) + Фх (t,— nNm} k 2                    )

Из условий допустимой погрешности интегрирования найдем значения n и Am . Величина шага интегрирования Am определяет погреш-

ность численного вычисления интегралов периодических тригонометрических функций. Например, для обеспечения погрешности вычисления Л< 1% тригонометрической функции с периодом Т достаточно, чтобы шаг интегрирования был равен A m = Т/20 .

п               Г mNt

Период функции sinl--- k 2

Т sin

4 л Ntt .

mj^u₀££₀ , m

a

££0 '

a

££ ₀

.

Таким образом, оценить период можно для обоих случаев:

T cos ( m )

2 л

t

N t

, m

a

t

X.

2 л

N t

MM 0 ^CT

2 m

, m

^££ 0

,

^a_ . (10)

x V ц^ 0 ££ 0

^££ 0

Из формулы (9) видно, что шаг интегрирования в общем случае является функцией от частоты:

N m ( m ) = min [ ^{T si} 2₀ ^{T cos ( m )}^ .       (11)

Таким образом, выражение (7) преобразуется к новому виду, что означает переход к интегрированию с переменным шагом:

f x ^{( t} , ^{n ) = A} л

Г^ф x ^{( t ,0 ) +}

n

+ 2

I - = 1

Ф х ^{( t , m} i — 1 ^{+N m} ( m -— 1 )) + ⁺ Ф х ^{( t , m} i — i ^—NmV^m i—^ ),

^{N m} ( m — 1 ⁾

I

. (12)

Следующим действием является определение n или границ интегрирования. Для этого необходимо вычислить значение n , после которого вычислением оставшейся части интеграла (1) можно пренебречь. При вычислении значения функции (11) значение n можно не задавать заранее, а определить его по ходу выполнения вычислений.

При достаточно больших значениях m составляющая волнового вектора k X ( m ) практически не меняется:

^k X ^{( m )} =

^u ₀ m\7 a ² + e ²e 2 m ² — ee ₀ m

Период функции cos ^^ tm — k"_х ( m ) x —

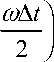
ди ₀ ££ ₀ Q a ²/ e ²e ₀ ² m ² +1 — 1) al^^ d 2                 2 ee ₀

определяется через приближенное значение параметра k X ( m ) :

Обозначим N m _T приращение частоты, соответствующее периоду T _sin • T _cos ( m ) и, подставив их, рассмотрим следующий интеграл:

у +Д у

I X ( t ) - j

У

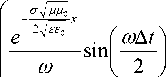
• cos I y | t - x ■Jauee III

d m . (14)

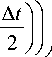
При бесконечном увеличении значения у интеграл (13) стремится к 0, поэтому ряд (12) сходится при n ^ ^ и может быть вычислен с заданным требованием точности. Если значения функции (11) практически не отличаются при n и n + ДУ _т / Ду , то интеграл (1) можно считать вычисленным.

Общий алгоритм вычисления формы результирующего импульсного сигнала, прошедшего через среду при зондировании её сигналом с заданными характеристиками имеет следующий вид.

Шаг 1 . Задание границ отображения графика t l и t r , определение количества точек m на графике, вычисление шага приращения ^Д t ^{- (t}r ^- U И m ^- 1 ) .

Шаг 2 . Начальная точка графика t — t_l .

Шаг 3. По формуле (11) вычисляется значение результирующего сигнала в точке t .

Шаг 3.1 . Задается начальное значение n _— 0 .

Шаг 3.2. По формулам (7) и (9) определяются периоды, вычисляется приращение Ду по формуле (10).

Шаг 3.3. Рассчитывается значение функции f_x ( t, n ) по формуле (11).

Шаг 3.4. Увеличивается приближение n — n + 1 , соответственно у — у + Д у .

f_x ( t , n /2 ) - f_x ( t , n ) xx

Шаг 3.5. Если                  меньше

I f x ( t , n )

некоего наперед заданного e , то приближенное вычисление точки считается завершенным. В противном случае возвращаемся к шагу 3.2.

Шаг 4. Аналогично шагу 3 вычисляется значение мнимой части в точке t .

Шаг 5. На графиках отмечаются вещественная и мнимая точки, а также величина модуля сигнала в точке t .

Шаг 6. t — t + Д t . Если t >  t_r , то алгоритм завершается, иначе переходим к шагу 3.

Следуя этим шагам и применяя интегрирование с переменным шагом, мы имеем возможность численно определить значение интеграла вида (1) на бесконечном промежутке за конечное число операций. Аналогично можно вычислить мнимую составляющую формулы 1.

Обобщая разработанный алгоритм на вычисление несобственных интегралов от функции произвольного вида, следует определить некоторые требования к подынтегральной функции: она должна быть колебательно-затухающей и обладать возможностью оценки своего значения при значениях аргумента, стремящихся к ^ .

Для иллюстрации приведенных расчетов разработана программа ЭВМ, реализующая указанный алгоритм. На рис. 1 приведены результаты расчета распространения прямоугольного электромагнитного импульса длительностью Дt = 10^-7 с, амплитуды A = 1, через среду с проводимостью о = 10^-17 Сим, относительной диэлектрической проницаемостью e = 2, магнитной проницаемостью Ц = 1 для точек контроля, находящихся на расстоянии 1 м, 50 м и 100 м от точки излучения. Графики иллюстрируют время прихода импульса в заданную точку, затухание и искажение его формы в зависимости от

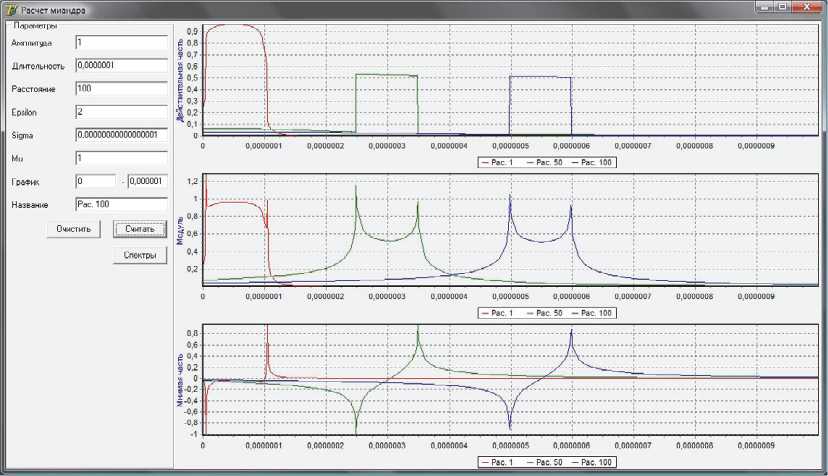
Рис. 1. Результаты расчета распространения прямоугольного электромагнитного импульса в поглощающей среде

расстояния. При этом действительная часть импульса соответствует его физическому содержанию, которое наблюдается на экране осциллографа. Мнимая часть позволяет с высокой точностью фиксировать временные параметры импульса (момент прихода и длительность), так как на фронтах импульса его мнимая составляющая имеет острый, явно выраженный экстремум. Причем минимум на переднем фронте, максимум – на заднем. Это дает возможность идентифицировать “тело” импульса при периодических импульсных облучениях. Модуль позволяет с высокой точностью определить энергетические характеристики, вычислить полные, активные и реактивные потери, обусловленные движением импульса в среде.

Программа, реализующая разработанный алгоритм, с высокой скоростью вычисляет несоб- ственные интегралы от сложных функций с заранее заданной погрешностью, что позволяет использовать их в управляющих информационно-аналитических системах, работающих в реальном времени.