Алгоритм численного решения задачи коши для уравнений пластичности треска

B.D. Annin, V.V. Alyokhin and V.V. Ostapenko

Lavrentyev Institute of Hydrodynamics SB RAS, Novosibirsk, 630090, Russia

The problem of propagation of plastic zones in an unbounded medium from the boundary of a convex surface under normal pressure, tangential forces and given velocities is studied. When the medium is in the state of full plasticity, the system of quasistatic ideal plasticity Tresca equations describing the stress-strain state is hyperbolic. The difference scheme applied to hyperbolic systems of equations is proposed for the numerical solution of this system.

В случае полной пластичности квазистатические уравнения идеальной пластичности Треска для определения напряжений имеют вид [1]

d t d t ₂ d t ₃ „

⁺w, = ^{0 ;}

t 1 ^{— (} ° 11 ’ ° 12 ’ ° 13 ) ’   t 2 ^{— (} ° 21 ’ ° 22 ’ ° 23 ) ’ t 3 ^{— (} ° 31 ’ ° 32 ’ ° 33 ) ’                            ⁽²⁾

° ij = °⁶ i j ^{+ 2} k ^£

n i n j

- ¹ ^.

₃ ij

° = 3 ° ij ⁵ ij ’ ^{e =± 1} ’

П\ + П 2 + П3 — 1’ где oij — компоненты симметричного тензора напряжений в декартовой системе координат (x1,x2,x3) с базисом e1,e2,e3; ° — среднее напряжение; 3ij — символ Кронекера; к — предел текучести при чистом сдвиге; n — niei — единичный собственный вектор, соответствующий главному напряжению

а = а +— k e, 1₃

два других главных напряжения совпадают:

а 2 = а з = а - —k e.

По повторяющимся индексам проводится суммирование от 1 до 3.

Определяемый равенствами (2) с учетом (3) тензор напряжений удовлетворяет условию пластичности Треска:

max( | а 1 - а ₂ |,| а ₂ - а ₃ |,| а ₃ - а 1 | ) = 2 к .

Зависящие от x1, x2, x3 функции а, n1, n2, n3 определяются из системы уравнений первого порядка, получаемой путем подстановки выражений (2) и (3) в (1). Эта система является гиперболической и имеет вид д n    д n    д n    _ n ^-1 + n2 —1 + n3 —1 + nxu = дx 2     дx3

д х 1

д p д x 1

д n2    д n    д n    _    дp n1 —2 + n 2 —2 + n3 —2 + n 2V =--, д x1      дx 2     д x3           дx 2

д n3     д n3     д n3     _     дp n1--+ n 2--+ n3--+ n 3U =--, дx1     дx 2     д x3           дx3

n , + n 2 + П з = 1 ,

^д n i    ^д n 2    ^д n 3

V =11, д x 1   д x ₂    д x ₃

а 1

.

2 k e 3

Свойства системы (6) рассмотрены в работах [2–4].

Поле скоростей перемещений u = ( u 1 , u ₂ , u ₃)^т в случае полной пластичности определяется из системы соотношений, включающей в себя условие несжимаемости среды

e ll ⁺ e 22 ⁺ e 33 = 0

и условие, что единичный собственный вектор n = n i e i , соответствующий главному напряжению (4), также является собственным вектором тензора скоростей деформаций ( e_ij )

e ll	e 12	e i3		n ,	= Л	n 1	1	Г д u д ui ) i эГ d x" < j        i 7
e 21	e 22	e 23	■	n 2		n 2	’ ij 2
, e 31	e 32	e 33 .		. n 3 .		. n 3 .

где Л — собственное значение тензора скоростей деформации ( e ij ).

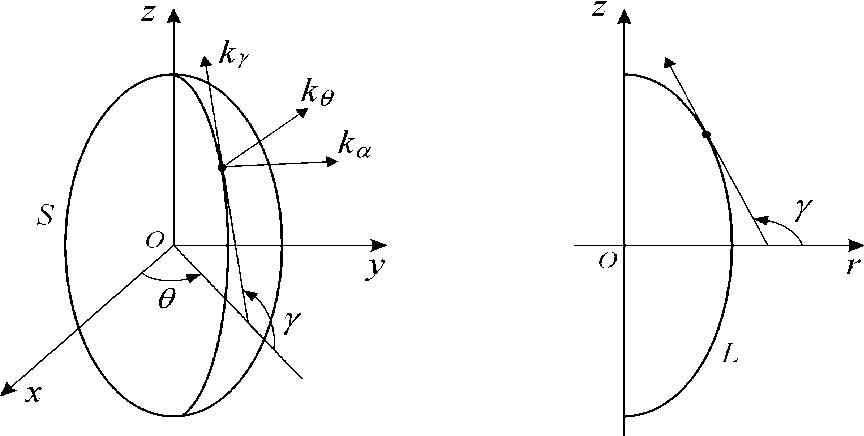
а                                         б

Ортогональная криволинейная система координат ( а, 9, у ): а — координатная поверхность S ( а = 0) и базисные векторы k _а , k ₉ , k _Y ; б — образующая L координатной поверхности

Для решения задачи о распространении зон пластического состояния от границы выпуклой поверхности, на которой действуют нормальное давление, касательные усилия и заданны скорости перемещений, используем численные алгоритмы гидромеханики [5-7].

Пусть S — достаточно гладкая замкнутая выпуклая поверхность, причем начало координат системы ( x , y , z ) лежит внутри S (Рис., а). Поверхность S образована вращением выпуклой кривой L (см. рисунок, б ), расположенной в плоскости ( r , z ) , где r = ( x ² + y 2 )^{1 1 2}, причем кривая L пересекает ось z под прямыми углами, а радиус кривизны р кривой L в любой ее точке не меньше р * >  0 .

Уравнения кривой L запишем в параметрическом виде:

z х dF(y)        _ х . z х dF(y) ._ r (y) =       cos Y + F (Y)sin Y, z (Y) =       sm Y - F (Y)cos Y-(9)

dY

Здесь Y — угол между касательной и осью r; F ( y) — опорная функция контура L. Очевидно, что r(y) ^ 0 при 0 < Y ^ п. Радиус кривизны кривой L вычисляется по формуле р = P(Y> = ^^dr^p) = F(Y) + d F(J) ^ P* > 0-cos y dY

Уравнения поверхности S запишем в виде

X s ( 9, Y ) =

y s ( 9, Y ) =

dF ( Y ) d Y

cos y + F ( Y )sin Y

dF ( Y ) d Y

cos y + F ( Y )sin Y

cos 9 ,

sin 9 ,

dF ( γ )

z ( θ , γ ) =       sin γ - F ( γ )cos γ .

S         _{d γ}

Введем ортогональную криволинейную систему координат ( α , θ , γ ) :

x (a,9, Y) = dF(Y)             . cos Y + (F (Y) + a)sin y _ dY                       J cosθ, y(α,θ,γ) = "dF(Y)                        " cosγ+(F(γ)+α)sinγ L dY sin 9, dF(γ)

z(α,θ,γ) =      sinγ-(F(γ) +α)cosγ, dγ

α ≥ 0 , 0 ≤ γ ≤ π , 0 ≤ θ ≤ 2 π .

Якобиан преобразования координат J ( α , θ , γ ) неотрицателен:

J ( α , θ , γ ) = ^{D ( x , y , z )} = ( ρ ( γ ) + α )( r ( γ ) + α sin γ ) ≥ 0 .

D ( α , θ , γ )

Из (12) следует, что поверхность α = const представляет собой поверхность, равноудаленную от поверхности S . Выражения для единичных векторов координатных линий (Рис., а) имеют вид

kα= (sinγcosθ,sinγsinθ, -cosγ)т, kθ= (-sinθ, cosθ, 0)т, kγ= (cosγcosθ, cosγsinθ, sinγ)т.

Запишем уравнения равновесия (1)–(3) в ортогональной системе координат ( α , θ , γ ) . Напряжения σ_αα , σ_αθ , σ_αγ , σ_θθ , σ_θγ , σ_γγ удовлетворяют уравнениям

∂ t ∂ t ∂ t

^α + ^θ + ^γ = 0

∂ α ∂ θ ∂ γ

где

t _α = H _θ H _γ ( σ_αα k _α + σ_αθ k _θ + σ_αγ k _γ ) , t _θ = H _α H _γ ( σ_αθ k _α + σ_θθ k _θ + σ_θγ k _γ ) , t _γ = H _α H _θ ( σ_αγ k _α + σ_θγ k _θ + σ_γγ k _γ );

H _α = 1 , H _θ = r ( γ ) + α sin γ , H _γ = ρ ( γ ) + α .

Исключая из системы (14) с учетом (15) базисные векторы (13), запишем ее в форме неоднородной системы законов сохранения

∂ u ∂ v ∂ w

+   +    = f ,

∂ α ∂ θ ∂ γ

где

u = H ₉ H _y u * , v = H _y v * , w = H ₉ w * ;

^u * = ( ^C aa , ^ «9 , ^C ay ) т , v * = ^(c« 9 , ^ 99 , ^C 9y ) т , w * = ( ^C ay , ^C 9y , ^ уу ) т ;

f =

^H y ^C 99 Sin Y ⁺ HC yy

^- H y ( C y cos y + о „9 sin y ) d Hg

-^99 ^- H 9 ^ ay

^ cycy — P + Псу ,   ^ суА — ПууПд ,   Cv — ПсуП-v;

aa г a7 au a о7 ay a y

^c 99 = p + n 9 ,   Q yy = p + n_y ,   ^c 9y = n 9 n y .

В выражениях (У0) и (У1) напряжения a_aa , c_a9 , a_ay , с₉₉ , a_y , a_9y — компоненты напряжения a ij (3) в ортогональной криволинейной системе координат ( a, 9, у ), деленные на У k e ; p = с / (У к £ ) - 1 / 3. Величины n _a , n ₉ , n _y представляют собой компоненты единичного собственного вектора n , соответствующего главному напряжению (4) в системе координат ( a , 9 , у ):

n = n _a k a + n ₉ k 9 + n _y k y , n a + n 9 + n ^y = 1 .

Векторное уравнение (17) и соотношение (22) образуют замкнутую систему для определения величин p , n _a , n ₉ , n _y как функций a , 9 , y .

Запишем теперь систему уравнений (7), (8) для поля скоростей перемещений u = ( u _a , u ₉ , u _y )^т в ортогональной системе координат ( a , 9 , у ). Смещения u _a , u ₉ , u _y удовлетворяют линейной неоднородной гиперболической системе уравнений

d u             . d u            . d u „

—+ A ( a , 9 , y )—+ B ( a , 9 , y )— = f , d a          d 9          d y

где

	0	1	0
		H 9
	1		n
A ( a , 9 , y ) =		9	Y
	H 9	n a H 9	n a H 9
	0	0	n 9
	L		n a H 9

	1 0     0     ---
	n
B ( a , 9 , y ) =	0  —Y—  0
	n a H y
	1      П 9     У n y
	_ H y   n a H y   n a H y

V He

1 )

+ — UY )

' a

cos у

u Y

f =

( sin Y n Y cos Y )

V H e     ⁿ a ^H e )

2 n ^e ( u„ sin Y+u_v cos / ) + 2 ^ n ^e n_aH_e “ ⁷ n« a e a

^{2 n} Y      . n e cos/„ . 1     . о i n Y

U„ +Ufl +Uv + 2Л naH a n„H9 e Hv Y n„ ay      a e      у       a

^ = I e ee ⁽ n a + n e ) + e yy ⁽ n a + n 2 ) ⁺ 2 e n e n Y I / ( 1 ^{- 2} n a

i eee   и

He L

d u _e e

+ u _a sin y + u _Y cos Y

e eYY

H

d u _v

"T--+ ua

dY

2 e =   d u e +

” H , Sy H _e L

d u _Y

—- - u_A cos Y de ⁹

функции n _a , n _e , n _Y находятся из системы (17), (22).

Для систем (17), (22) и (23) поставим следующие задачи Коши. На поверхности S , определяемой формулами (11), то есть a = 0, 0 <  e <  2 п , 0 <  у <  п , заданы начальные значения функций p , n _a , n _e , n _y и u _a , u _e , u _y . Требуется найти эти функции при a >  0 . При такой постановке задач Коши величина a представляет собой независимую эволюционную переменную, а системы (17), (22) и (23) решаются последовательно и, по крайней мере вблизи поверхности А , являются a -гиперболическими [5, 6]. Для их численного решения используем разностные схемы, применяемые для гиперболических систем законов сохранения [5, 7].

В прямоугольной области П = { e , Y : 0 <  e <  2 п , 0 <  Y <  п } введем равномерную разностную сетку e = ih 1 , Y j = jh ₂ , i = 1 , N 1 , j = 1 , N ₂ , где h i = 2 п / N 1 , h ₂ = п / ( N ₂ - 1) — постоянные шаги сетки. При i = 1 , N 1 , j = 2 , N ₂ - 1 аппроксимируем систему (17) следующей явной двухслойной по времени и симметричной по пространству разностной схемой

—n+1  —n —n —n — n — n u ij - u ij + v i+1, j- v i-1,j + w i, j+1- w i, j-1

= f n + W ij ,

T _n           2 h 1             2 h ₂

где n     nn       n     n n n _ Г v i+1. j - 2v ij + v i-1. j , г w i- j+1 - 2w ij + w i- j-1

искусственная   вязкость,

W ij = С1--------;---------+C C2---------;---------- hh коэффициенты C1 и C2 которой подбираются из тестовых расчетов.

В (24) и ниже для всех сеточных функций введены сокращенные обозначения:

n — 1

g n = ^{g a} 9 , Y j ) , g n = g ⁽ a 9 , Y j X ^a n = E ^T k , ^a 0 = ⁰ k = 0

( т _к — переменный шаг по эволюционной переменной a ). Поскольку искомое решение является периодическим по переменной 9 , в формуле (24) предполагается, что 9 о = 9 n_x , 9 n _{i +} i = 9 1 .

В граничных узлах j = 1 и j = N ₂, то есть в полюсах у = 0 и У = п , происходит вырождение уравнений (17) по переменной 9 . Известно, что для гладкой поверхности вращения S (11) в каждом из полюсов оба главных радиуса кривизны r 1 ( Y ) = p (Y) (10) и r ₂( Y ) = r ( Y ) / sin Y , где r ( Y ) определяется формулой (9), совпадают и равны р (0) и р ( п ) соответственно. Анализ уравнений (17) показывает, что при у ^ 0 и у ^ п систему (17) можно записать в виде

Э 2

—( H 2 u ) = f ,                                                         (25)

da Y где f = Hy [^99 + ^YY ,-°a9 ,—^aY ]т ’ HY = P(Y) + a, У = 0>п-

Для приближенного вычисления сеточных функций nnn n i = 1, N1

gi1 = g1,  g iN 2 = g N 2, в граничных узлах j = 1 и j = N2 можно использовать следующую разностную схему при аппроксимации системы (25):

( H u * ) m¹ — ( h Y u * ) m             _M

--------= f m , ^m = 1 , N 2 .

^T n

После нахождения величин o^,aa9,oaY на (n +1)-ом слое из разностных уравнений (24), (26) с учетом (16), (18), (19) основные сеточные функции p, na, n9, nY в каждом узле (i, j) этого слоя определяются из системы алгебраических уравнений (20), (22). Решая эту систему в предположении, что в процессе счета d = ^а9 +а^ < 1 / 4, получим n» = V(1 + V1 — 4 d )/2, p = ^,„ — n 2, n9 = ^,А ln„ , nv = ^, ln„. a                              aa a9 ao a          ay a

Величины a₉₉ , a_}7 , a_9Y , входящие в систему (17)-(19), вычисляются по формулам (21).

После определения функций n _a , n ₉ , n _Y на ( n + 1)-ом слое скорости смещений u _a , u ₉ , u _Y находятся из системы (23), которая при i = 1 , N 1 , j = 2 , N ₂ — 1 аппроксимируется следующей разностной схемой:

n+1 n          n        n              n        n uij uij , n" ui+1-j ui—I-j , on ui,j+1 ui,j-1

--+ Ai --+ Ba------------

T _n               2 h 1          ij      2 h ₂

= f n + W n ,

n   nn    n   nn

„_гИ       u i + 1 - / - 2 u ij ⁺ u i-1-j ,      u i , j + 1 - 2 u ij ⁺ u i , j - 1

где  Wn = 4--------------~+C2—-----------—    — искусственная вязкость, h1                         h2

коэффициенты C ₁ и C ₂ которой те же самые, что и в разностной схеме (24).

В граничных узлах j = 1 и j = N2 (в полюсах у = 0 и у = п), где происходит вырождение уравнений (23) по переменной 6 систему (23) можно записать в виде

du да

где

f =

--U« ,--- U ^а H Y H Y

' 6

^{2 n}6 „ -эа^пе ¹ „

U„ + 2Л,Uv naH       na H Y la Y                    4а        Y

т

--^- u„ + 2^— , n„H, ^а n„

4а Y                    4а

Л = ^и а ^{1 + n} a н _У 1 - 2 n a ’

H _Y = pY + а, у = 0 , п.

Для приближенного вычисления сеточных функций nnn n u i 1 = u1,  u iN 2 = u N 2,  i = 1, N1

в граничных узлах j = 1 и j = N ₂ можно использовать следующую разностную схему при аппроксимации системы (28):

n+1     n um um nn

---1= f m , ^T n

m = 1 , N 2 .

В разностных схемах (24), (26) и (27), (29) шаг T _n по эволюционной переменной а определяется из условия устойчивости Куранта [7] по формуле

к * a n + min р ( / _у ) min( \, h 2 )

^T n

_ j _ n -1 n n n max(Zij,(л )ij,Pij,Vij) i, j где Л,Л 1,p,v — скорости распространения малых возмущений вблизи поверхности S (an); Л = V (1 + 2 a) / (1 - 2 a); р = b + b2 +1 / H6 ; V = c + c2 +1 / HY ; a = na n6 + n2 ; b = n6 / (naH6); c = nY / (naHY); р и v — это положительные максимальные собственные значения матриц A(a,6, Y) и B(а,6, Y) системы (23); к* < 1 — коэффициент запаса в условии устойчивости.

Численные эксперименты показали хорошую работоспособность предложенного алгоритма.

Работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований (проект № 08-01-00749) и Совета по грантам Президента РФ для ведущих научных школ (грант НШ-3066.2008.1).