Алгоритм фильтрации рентгеновских томограмм методом адаптации размера окна фильтра к локальным характеристикам изображения

Алгоритмы фильтрации изображений с адаптацией размеров апертуры были представлены в статьях Воскобойникова, Белявцева и Бронникова [1, 2]. Известно, что степень сглаживания сигналов зависит от размеров апертуры фильтра. При малом размере апертуры фильтра обработке подвергается меньшее число значений, что обеспечивает лучшее сохранение контрастных деталей сигнала, но при этом шум будет сглажен хуже. При большом размере апертуры фильтра сглаживание шума будет происходить лучше, однако при этом возможна «потеря» некоторых контрастных деталей, присутствующих в исходном сигнале. Таким образом, введение алгоритмов адаптации размеров апертуры позволяет улучшить качественные характеристики данного локального фильтра.

В настоящей статье предложен алгоритм фильтрации изображений с адаптацией размеров апертуры к локальным характеристикам этих изображений.

Описание алгоритма

Основой адаптивного алгоритма является выбор оптимальных параметров фильтрации: определение размера апертуры фильтра по локальным статистикам (локальное среднее, локальная дисперсия, дисперсия шума) и типа фильтра (медианный, скользящего среднего или комбинированный) в зависимости от локальных статистик изображения.

Входные параметры фильтра:

• ■    минимальный и максимальный горизонтальный размер апертуры;

• ■    минимальный и максимальный вертикальный размер апертуры;

• ■    значения параметров к и е , определяющих чувствительность алгоритма к адаптации. Описание выбора параметров приведено ниже.

Шаги алгоритма описаны ниже.

• 1.    Задаются ограничения на минимальный и максимальный размеры апертуры; задаются параметры k и ε .

• 2.    Первоначальный размер апертуры устанавливается минимальным.

• 3.    Флаг выбора размеров апертуры устанавливается в 0.

• 4.    Флаги изменения размеров апертуры устанавливаются в 1.

• 5.    Пока флаг выбора размеров апертуры не равен 1, выполняется подбор размеров апертуры.

• 6.    При выбранном размере апертуры для выбранной точки рассчитывается медиана.

• 7.    Оценивается дисперсия шума.

• 8.    Рассчитываются средние значения яркости по строкам и столбцам изображения.

• 9.    Рассчитываются среднеквадратические отклонения по строкам и столбцам изображения.

• 10.    Производится проверка условия превышения среднеквадратическими отклонениями заданного уровня шума.

• 11.    В случае истинности условия для строки или столбца соответствующий размер апертуры уменьшается, устанавливаются флаги изменения размеров апертуры.

• 12.    В случае ложности условия соответствующий размер апертуры увеличивается, устанавливаются флаги изменения размеров апертуры.

• 13.    Производится проверка выхода установленных размеров апертуры за пределы минимальных и максимальных размеров.

• 14.    В случае достижения одним из размеров фильтра предельного значения расчёт размеров апертуры заканчивается, флаг выбора размера устанавливается в единицу.

• 15.    Осуществляется проверка критерия останова: если знак приращения размеров апертуры меняется на противоположный, то флаг выбора устанавливается 1, иначе флаг выбора остаётся равным 0.

• 16.    Если флаг выбора равен 0, осуществляется переход к шагу 5.

• 17.    Для выбранного размера апертуры рассчитывается медиана.

• 18.    Для выбранного размера апертуры рассчитывается дисперсия шума.

• 19.    Для выбранного размера апертуры рассчитывается среднее значение.

• 20.    Для выбранного размера апертуры рассчитывается локальная дисперсия.

• 21.    Оценивается и корректируется величина ц .

• 22.    По рассчитанной величине ц определяется тип фильтра.

• 23.    При рекурсивной реализации алгоритма значению x™ ( k , l ) текущей точки присваивается рассчитанное значение f _вых .

Оценка параметров

Параметр k

На шаге 10 проводится проверка неравенств:

v 2 ( k , l ) > k o M ;

v2(k,l)> k°M, где v2 (k, l) и v2 (k, l) - среднеквадратическое отклонение по строкам и столбцам, koM - оценка шума.

В случае истинности условия для строки или столбца соответствующий размер апертуры уменьшается, в обратном случае – увеличивается.

Соответственно, возможные варианты выбора параметра k :

• ■    k < 1, если требуется удерживать размеры апертуры, близкие к минимальным;

• ■    k = 1, если требуется расчёт по действительной величине шума;

• ■    k > 1, если требуется удерживать размеры апертуры, близкие к максимальным.

Параметр E

На шаге 21 оценивается величина ц :

XD ц = 1--,

DISP где XD – дисперсия шума; DISP – локальная дисперсия.

Величина ц может принимать следующие значения:

• ■    ц = 1, если локальная дисперсия значительно превосходит дисперсию шума (происходит резкое изменение изображения);

• ■    0 < ц <  1, если размеры локальной дисперсии и дисперсии шума сопоставимы;

• ■    ц = 0, если дисперсия шума превосходит локальную дисперсию (отклонения обусловлены шумом).

По значениям ц и е опред еляется тип фильтра:

	f M , е сли 1 -е<ц< 1;
У в ЫХ	ц f M + ( 1 - ц ) f CP , если е <ц < 1 - е ; f CP , е с ли 0 < ц< е .

С оотв е тс тв е н н о, и ме ю т смы с л зн а че н и я ее ( 0,0; 0,5 ) . Чем большее значение имеет е , тем ши ре п олосы ме д иа н н ог о фи л ьтра и фильтра скользящего среднего. При ма лых зн а че н и ях е р а с ш и ряе т с я п олоса к ом би н и ров а н н ого фильтра: при е = 0,05 полоса составит ( 0,05; 0,95 ) .

Результаты вычислительных экспериментов

Описание тестового изображения

В к аче с тв е те с тов о го и з об раже н и я использовалось изображение, восстановленное с помощью реконструктора [3, 4] п о п роек ц ион н ы м д а нн ым ф а н тома Ш е п па– Логана. Для ухудшения ка че с тв а и зоб раже н и я н а п роекционные данные был наложен гауссовый бел ый ш у м. Ед и н и чн ы е ка н а льные о ш и бк и б ы ли с мод е ли р ов аны наложением импульсного шума.

Проек ци он н ы е д а н ны е п ред с та в л е н ы н а рис. 1.

а)

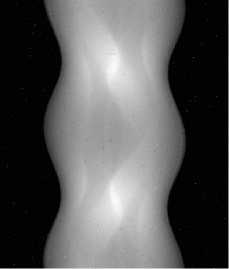
б)

Рис. 1. Фантом Шеппа–Логана: а – исходное изображение; б – зашумлённые проекционные данные

Результаты фильтрации

Пол ученн ое изобра ж е н ие б ыл о об р а б ота но предлагаемым фильтром, а также медианным ф ил ьтром и фи л ьтром ск ол ьзящего среднего в один и два прохода. Результаты фи л ьтра ц и и п ре дставлены в табл. 1.

Оц е н к а с ред н ек в а д р а ти ческой ошибки фильтрации производилась по ф о рмул е

IJ             I J

A i

= ЕЕ ( У, , j - К1 ) 2 /ЕЕ j i = 1 j = 1                    / i = 1 j = 1

где f _{i , j} – зн а чени е отфи льтров а н н ой точк и и з обра ж е н и я; f _{i , j} – значение исходной точки изобра ж е н и я б е з и ск аже н и й и шума .

Оц е н к а от н осит ельн ой о ш и б к и фи ль трации производилась по формуле

^A 2

I J              I J I J

= ЕЕ ( 7, - j ЕЕ fj

_ i = 1 j = 1                    / i = 1 j = 1

100%,

где f _{i , j} – зн а чени е отфи льтров а н н ой точк и и з обра ж е н и я; f _{i , j} – значение исходной точки изобра ж е н и я б е з и ск аже н и й и шума .

Таблица 1

Параметры фильтрации

№ п/п	П ара ме тры	А 1 , 10-4	А 2 , %
1	k = 0,95, e = 0,05	3,20	1,79
2	k = 1,00, e = 0,15	3,16	1,78
3	k = 1,05, e = 0,15	3,15	1,77
4	k = 1,05, e = 0,25	3,16	1,78
5	k = 1,05, e = 0 , 15 (ре к у рс ив н о, 1 п роход)	2,89	1,70
6	k = 1,05, e = 0 , 15 (ре к у рс ив н о, 2 п роход)	2,65	1,63
7	ФСС, апертура 3 x 3 , 1 пр о ход	8,61	2,93
8	ФСС, апертура 3 x 3 , 2 пр о ход	9,91	3,15
9	ФСС, апертура 5 x 5 , 1 пр о ход	9,56	3,09
10	ФСС, апертура 5 x 5 , 2 пр о ход	15,00	3,87
11	МФ, апертура 3 x 3 , 1 прох од	3,55	1,89
12	МФ, апертура 3 x 3 , 2 прох од	2,30	1,52
13	МФ, апертура 5 x 5 , 1 прох од	1,77	1,33
14	МФ, апертура 5 x 5 , 2 прох од	1,32	1,15

Пол ученн ы е п рое к ц и он ные данные были восстановлены. Рассчитанные ошибк и фи ль тра ц и и представлены в табл. 2, в осс та н ов ле н ные и зобра ж е н и я п ре д с та в л е н ы н а ри с. 2.

а)

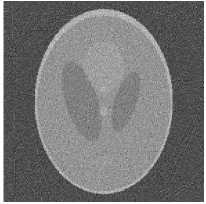
б)

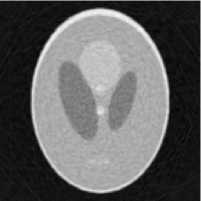
в)

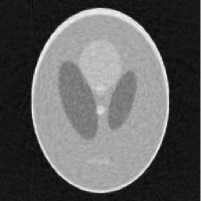
г)

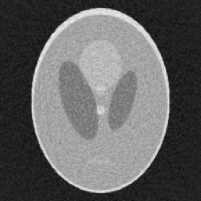
д)

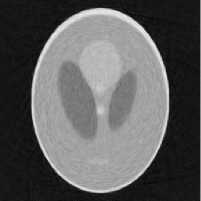
е)

Ошибки фильтрации

Таблица 2

№ п/п	П ара ме тры	А 1	А 2 , %
1	И зоб раж е н ие, восс т а н ов л е н ное с зашумлёнными проек ц ион н ыми д а н н ыми	0,2503	50,0
2	ФСС, апертура 5 x 5 , 1 пр о ход	0,0306	17,5
3	МФ, апертура 5 x 5 , 1 прох од	0,0295	17,2
4	Комб, k = 1,05, e = 0 , 15	0,0500	22,4
5	Комб, k = 1,05, e = 0 , 15, р е к у рс и в н о, 2 п рохо д а	0,0324	18,0

Рис. 2. Восстановленные изображения (1 проход): а – исходное изображение; б – изображение, восстановленное с зашумлёнными проекционными данными; в - фильтр скользящего среднего, апертура 5 x 5; г - медианный фильтр, апертура 5 x 5; д - предлагаемый комбинированный фильтр, к = 1,05, e = 0,15; е – предлагаемый комбинированный рекурсивный фильтр, k = 1,05, e = 0,15

По результатам фильтрации можно сделать вывод, что предлагаемый алгоритм даёт ошибку фильтрации меньшую, чем фильтр скользящего среднего, и сравнимую с ошибкой медианного фильтра. Наименьшая ошибка фильтрации достигается при значениях параметров к >  1, e = 0,15 .

Также можно сделать вывод, что при сравнимом объёме ошибок границы высококонтрастных объектов остаются более резкими, в монотонных областях содержится меньше “зернистости”, что является критичным в томографии.

Заключение

В результате исследований были решены следующие задачи:

• ■    проанализированы существующие адаптивные алгоритмы в области обработки изображений;

• ■    предъявлены требования к создаваемому алгоритму;

• ■    создан и протестирован алгоритм фильтрации изображений с адаптацией размеров апертуры и метода фильтрации к локальным характеристикам изображения;

• ■    оценены погрешности, даваемые алгоритмом, в сравнении с существующими методами фильтрации.

Предложенный алгоритм можно использовать для фильтрации проекционных данных КТ.