Алгоритм и численное решение нелинейного смешанного уравнения теплопроводности в пакете Python
Автор: Ханхасаев В.Н., Жамцаев Н.С.
Журнал: Вестник Бурятского государственного университета. Математика, информатика @vestnik-bsu-maths
Рубрика: Математическое моделирование и обработка данных
Статья в выпуске: 4, 2024 года.
Бесплатный доступ
В работе рассматривается математическая модель для смены режимов коммутации электрической дуги. В отличие от квазистационарного теплового режима амплитудного горения дуги, хорошо описываемого классическим параболическим уравнением теплопроводности, в области перехода переменного тока через 0, когда дугу отключают современными выключателями в среде элегаза, необходимо применять гиперболическое уравнение в связи с существенной нестационарностью протекаемого процесса. Отсюда возникает постановка начально-краевой задачи для нелинейного гиперболопараболического уравнения, а также необходимость ее исследования с учетом нелинейности коэффициента теплопроводности. Для нее разработаны алгоритм и программа численного решения в широко используемом в настоящее время пакете программирования Python с визуализацией в графическом пакете Matplotlib и применением метода неявных конечно-разностных схем для краевых условий первого рода.
Гиперболическое уравнение теплопроводности, метод конечных разностей, нелинейные уравнения смешанного типа, краевые условия первого рода
Короткий адрес: https://sciup.org/148330326
IDR: 148330326 | УДК: 51-7 | DOI: 10.18101/2304-5728-2024-4-48-57
Текст научной статьи Алгоритм и численное решение нелинейного смешанного уравнения теплопроводности в пакете Python
Работа выполнена при финансовой поддержке гранта РНФ №23-21-00269,
Процессы нагревания и охлаждения металлов и других материалов представляют собой важную область исследований в промышленности, где тепловые явления играют ключевую роль и их тепловые характеристики подчиняются различным нелинейным явлениям. Одним из важных аспектов при исследовании этих процессов является учет резкого нагрева стержня (например, при сварке), возникающего между поверхностью металла и окружающей средой [7] , что существенно влияет на вид зависимости удельной теплопроводности от температуры стержня и боковой теплообмен на его поверхности, а также от внутренних источников тепла.
В работах Ханхасаева В.Н. [3] – [5] изучаются математические модели для численного решения различных линейных и нелинейных гиперболо - параболических уравнений теплопроводности с созданием программ в пакетах программирования Фортран(Fortran) и Mathcad-15, широко применяемых в инженерной среде. Для исследования процессов, происходящих за короткий промежуток времени в частности, при отключении электрической дуги с помощью современных коммутационных аппаратов, часто используют обобщённый закон Фурье для расчёта температурных полей [3] . Фронт возникающей тепловой волны отражается тогда гиперболическим уравнением теплопроводности, которое позволяет моделировать распространение тепловых волн с конечной скоростью, в отличие от параболического уравнения, соответствующего классическому закону Фурье [3] - [6] .
В данной работе исследуется одна из нелинейных постановок аналогичных начально-краевых задач, но с созданием существенно нового алгоритма и метода численного решения по неявной разностной схеме в широко применяемом в настоящее время языке программирования Python с визуализацией в графическом пакете Matplotlib.
-
1 Постановка начально-краевой задачи
Изучая протекаемые события, разработаем математическую модель упомянутого процесса одномерной теплопроводности, представленной квазилинейным гиперболо-параболическим уравнением:
∂ 2 u ∂u ∂ ∂u
b(x,t) -^2 + a(x,t)^r = a-(4x,t,u)a~) + c(x,t)u + f (x,t), ∂t ∂t ∂x ∂x где b(x, t) — тепловой релаксационный коэффициент, a(x, t) — произведение удельной плотности на удельную теплоемкость, Л(х, t, и) — нелинейный коэффициент теплопроводности, c(x, t) — коэффициент боковой теплоотдачи на поверхности дуги, f (x, t) — внутренний источник теплового нагрева или охлаждения.
Краевые условия первого рода задают температуру левого и правого концов дуги:
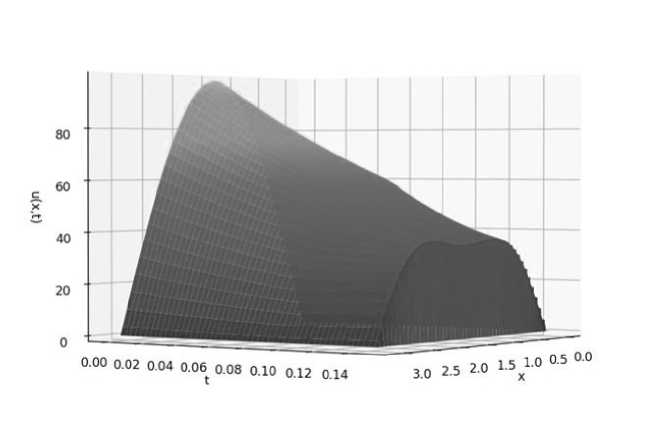
u(0, t) = go(t),u(X, t) = gi(t), 0 Начальное условие определяет распределение температуры в электрической дуге в начальный момент времени t = 0: u(x, 0) = uo(x), 0 < x < X. При 0 < t < T/2, когда процесс теплопроводности квазистациона-рен, мы принимаем b(x,t) =0 и уравнение (1) принимает вид квазилинейного параболического уравнения: a(x, t) lU = Г (Л(х, t,u)dU)+ c(x, t)u + f (x, t).(4) ∂t ∂x∂x 2 Алгоритм численного решения параболического этапа Проводим дискретизацию по переменным x и t, вводя дискретную сеточную функцию Uijдля приближенного решения начально-краевой задачи (2,3,4). Составим конечно-разностное уравнение дискретной задачи параболического этапа. В этом случае, неявная разностная схема будет выглядеть так: Uj- Uj-1 a(xi,tj) ' Ti = h2 ji(U^ - Uij) - Xj-1(Ui - Uti)] + + c(xi,tj)Uj + f (xi,tj), (5) где теплопроводности λij± 1в выражениях для сеточных аналогов тепловых потоков (эффективные теплопроводности отрезков [xi-i,x{], [xi,Xi+i]) определим по формулам: X 1 =[X(Xi,tj, 0.5(U±1 + Uj-1))]. i± 2 Здесь, в изучаемой схеме (5) эффективные теплопроводности λij± 1 находятся по значениям Uij-1 предыдущего временного слоя по формулам (6), т.е. при решении разностных уравнений относительно значений Uij на текущем временном слое tj эти коэффициенты известны и система (5) является линейной относительно Uij . Решение Uij находим методом прогонки [1]. Различие алгоритма решения квазилинейной задачи от линейной постановки [2] состоит в том, что на каждом шаге по времени необходимо вычислять новые значения коэффициента теплопроводности Л(х, t, и) и заново определять коэффициенты ai , bi , ci , di канонической системы уравнений с трехдиагональной матрицей. Перегруппируем в левой части уравнения (5) члены, содержащие значения дискретной функции U на j-ом шаге по времени, а в правую часть перебросим оставшиеся члены: тЛ^ 1 тЛ11 тЛ11 тЛ11 —h2 Uj+i + (-c(xi,tj)т+—^г+h2+a(xi,tj))Uj - h2 UL1 = = a(xi,tj )Uj1+ f (xi,tj )т. (7) Выражения для коэффициентов ai , bi , ci , di канонической системы метода прогонки [1] можем получить из соответствующих уравнений разностной схемы: ai = - ' 2 h2 Tj1 bi = -c(xi,tj )т +h2 + τ λij-1 h22 + ax^tj', τ λij-1 ci = h2 ’ di = -a(xi,tj)Uj-1 - f (xi,tj)т. С учётом этих обозначений, равенство (7) будет иметь вид: aj + bUj + cU— + di = 0. (8) После определения всех требуемых компонентов, поиск решения системы уравнений (8) производится методом прогонки [1]-[2] с учетом нелинейного коэффициента теплопроводности. 3 Начальные условия для гиперболического этапа При T1 < t < T мы принимаем коэффициент тепловой релаксации b(x,t) > 0 и уравнение (1) принимает гиперболический тип, для которого задаем первое начальное условие u(x,T 1) из предыдущего расчета для параболического этапа при t = T1, а второе начальное условие для гиперболического уравнения мы получаем аппроксимацией первой производной из параболического этапа. Начальные условия гиперболического этапа тогда выглядят следующим образом: u(x, T1) = ui(x), 0 < x < X, (9) ∂u — (x, T1) = u2(x), 0 < x < X. (10) где ui(x) — интерполяция дискретной функции Um1 на отрезке 0 < x < X, a U2(x) — интерполяция дискретной аппроксимации первой производной по времени найденной дискретной функции U^1. Далее проводится численный расчет для гиперболического уравнения (1) на интервале m1 < j< m по неявной схеме с применением метода прогонки для дискретного уравнения. 4 Алгоритм численного решения гиперболического этапа Неявная разностная схема гиперболического этапа численного решения уравнения (1) принимает вид: Uj+1- 2Uj + Uj-1 Uj+1 b(xi,tj+i)-i------т2-----i--+ a(xt, tj+1) —— - Uj-1 2т = ■. j (+ - Uj+1) - 1 U - Uj-+!1)l+ + c(xi,tj+i)Ui+1 + f (xi,tj+i). (11) Проведем такую же группировку как на параболическом этапе: (- i+ 2 h- )Uij++11 + т2^j+1 т2^j+1 + (-c(xi,tj+1)T 2+--^2 +--^2 +--i, 2j'+1 ' b(xi,tj+1))Ui+1+ +(- h2 )Uij-+11 = = 2b(xi,tj+i)UiJ + т2f (xi,tj+i) + (akxlj1)! - b^tj+i^Uj 1. (12) В. Н. Ханхасаев, Н. С. Жамцаев. Алгоритм и численное решение нелинейного смешанного уравнения теплопроводности ... Получим коэффициенты: T j т ^ ai = (- h = (— - ), bi = (-c(xi,tj+1)T2 +^2 2 +h2 2 +, 2j+ + b(xi,tj+1)), di = -(2b(xi,tj+i)Ui + т2f (Xi,tj+1) + (a(xi,j+1)T - b(xi,tj+1))Ui-1). С учётом этих обозначений, равенство (12) будет иметь вид (8). После определения всех требуемых компонентов, поиск решения уравнения (11) с начально-краевыми условиями (9-18) производится методом прогонки, с учетом переменного коэффициента теплопроводности. 5 Повышение порядка аппроксимации В этом пункте повысим порядок аппроксимации по времени для второго начального условия гиперболического этапа (10), которое проведем аналогично схеме, указанной в работе Муняева С. И. [5], но с учетом квазилинейности уравнения (1) по коэффициенту теплопроводности. Второе начальное условие из (10) с аппроксимацией по времени первого порядка имеет вид: ди&,тi) = um um 1 ∂t τ Для получения второго порядка аппроксимации, запишем ряд Тейлора на точном решении u(x, t) по времени в окрестности t = T1 и со сдвигом по времени T2, обрывая его на второй производной: , \ m \ du(xi,T 1) т2 d2u(xi,T 1), u(xi,T 1 + т2) ~ u(xi,T 1)+ т2----777---- + —----772----, dt 2dt где, вторую производную выведем из уравнения (1): d2u(x,t) 1 d du(x,t) a(x,t) du(x,t) dt2 b(x, t) dx x, ,' u dx b(x, t) dt , cM1l(T , f (x,t) +b(x,t)u(x,t)+ b(x,t). Найдем отсюда неизвестное дискретное значение: ttmi+1 mml i du(xi,T 1) Ui = Ui+—at— т2 1 d + [ ' 2 Lb(xi,T 1) dx [X(xi,T 1,u) u^xx^l ] — a(xi,T 1) du(xi,T 1) c(xi,T 1)иm1 f (xi,T 1), b(xi,T 1) dt +b(xi,T 1) Ui+b(xi,T 1)] В результате, получаем второе начальное условие для расчета гиперболического этапа с повышением порядка аппроксимации по времени до 2-го: du(xi,T 1) = Um-Um— ∂t τ1 +T2[^2(U+ - Um1) - ' (Um - Um1)] - a(xi,T 1) — -U— , c(xi,T 1)Umi , f(xi,T 1) b(xi,T 1) ti + b(xi,T 1) i + b(xi,T 1) Приведенный выше алгоритм может быть легко реализован на различных языках программирования, в частности, с использованием пакета Python. Далее приводится пример конкретного расчета по этой программе с визуализацией полученного результата в графическом пакете Matplotlib. 6 Параметры конкретного расчета и график Входные данные : L = pi Длина стержня T1 = 0.1 Время моделирования (секунды) параболического этапа T2 = 0.05 Время моделирования (секунды) гиперболического этапа rho = 1 Плотность материала (кг/м3) N = 500 Количество узлов на стержне m1 = 100 Количество шагов по времени m2 = 50 Количество шагов по времени uo(x,to) = sin(x) * 100 A(x, t, u) = u2, c(x, t) = -10, f (x, t) = 0. Рис. 1. График поля температуры. Заключение Полученные результаты численного моделирования позволяют провести анализ влияния существенной нестационарности процесса резкого нагрева или охлаждения на теплопроводность и теплообмен в металлах и других материалах. Эти результаты, проведенные в пакете Python подтверждают численные расчеты других аспирантов Ханхасаева В.Н., полученные в пакете MathCad-15. Разработанный программный код представляет собой эффективный инструмент для изучения динамики изменения температуры в материале и может быть использован для оптимизации процессов нагревания и охлаждения.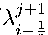
Список литературы Алгоритм и численное решение нелинейного смешанного уравнения теплопроводности в пакете Python
- Дульнев Г. Н., Парфенов В. Г., Сигалов А. В. Применение ЭВМ для решения задач теплообмена: учебное пособие для теплофизических и теплоэнергетических спец. вузов. Москва: Высшая школа, 1990. 207 с. EDN: ZXURGX
- Жамцаев Н. С. Алгоритм и численное решение линейного смешанного дифференциального уравнения в пакете Python // Динамические системы и компьютерные науки: теория и приложения (DYSC 2024): материалы VI Международной конференции. Иркутск: Изд-во ИГУ, 2024. С. 227. DOI: 10.26516/978-5-9624-2309-8.2024.1-224 EDN: CPRFST
- Ханхасаев В. Н., Баиров С. А. Моделирование распределения температуры при нагреве пластины с применением смешанного уравнения теплопроводности // Вестник БГУ. Математика, информатика. 2024. № 1. С. 37-45. EDN: IECYEY
- Ханхасаев В. Н., Дармахеев Э. В. О некоторых применениях гиперболического уравнения теплопроводности и методах его решения // Математические заметки СВФУ. 2018. Т. 25, № 1. С. 98-109. EDN: URISNO
- Ханхасаев В. Н., Муняев С. И. Численное решение третьей краевой задачи для нелинейного смешанного уравнения теплопроводности // Вестник БГУ. Математика, информатика. 2023. № 4. С. 14-21. EDN: GUPOQK
- Шашков А. Г., Бубнов В. А., Яновский С. Ю. Волновые явления теплопроводности. Системно-структурный подход. Москва: Едиториал УРРС, 2004. 296 с. EDN: QJMGPV
- Петрова Л. С. Математическое моделирование процессов нагрева кусочно-однородных тел с учетом релаксации теплового потока // Науковедение. 2017. Т. 9, № 1. URL: http//naukovedenie.ru/38TVN117.pdf. С. 11. EDN: YMXOXD


