Алгоритм и математическая модель формирования устойчивых цепочек поставок древесного сырья из регионов России: сравнение и анализ

Формирование устойчивых цепочек поставок сырья является базовой и серьезной проблемой любого предприятия. В ле- сопромышленной отрасли этот процесс усложнен тем, что выращивание леса до требуемых кондиций на арендованных у государства делянах представляет собой растянутый во времени и трудоемкий процесс. В связи с этим, а также из-за сложно- сти получения в аренду делян многие лесоперерабатывающие предприятия не имеют собственной сырьевой базы. Для их устойчивой работы без экономических потерь менеджменту предприятий необходимо принимать обоснованные управленческие решения по формированию устойчивых цепочек поставок сырья (Supply Chain Management, далее SCM) с внутреннего рынка региона, страны или международ- ных товарно-сырьевых бирж. При формировании на заданном горизонте планирования устойчивой цепочки поставок сырья необходимо учитывать фактор неопределенности и возможные риски. Это обусловливает стохастическую природу части параметров модели.

Как правило, при решении задач класса SCM используются различные модели. Так, например, для решения частного случая задач класса SCM – транспортных задач – часто используются линейные модели, которые, как известно, требуют большого объема оперативной памяти. Если свести интересующую проблему к задаче выпуклого программирования, то можно подобрать алгоритм, позволяющий находить оптимальное решение. Однако в случае с задачами класса формирования цепочек поставок сырья не всегда удается свести задачу к классу выпуклого про- граммирования [1] и необходимо разрабатывать авторский алгоритм и / или модифицировать уже имеющийся. Для решения общей задачи SCM с включением вероятностных процессов производства или транспортировки сырья используют нелинейные стохастические модели.

Процесс формирования цепочек поставок сырья усложняется еще и тем, что отсутствуют универсальные точные алгоритмы по поиску оптимального решения задач невыпуклого программирования. Более того, в [1–3] утверждается, что такого рода решений не существует, так как функционирование предприятий имеет большое количество вероятностных процессов, которые трудно учесть. Поэтому принято искать эффективное решение, которое отличается от оптимального тем, что для большинства вероятностных исходов такое решение является наилучшим из всех допустимых.

Отсюда вытекает еще одна трудность, с которой сталкивается предприятие при формировании плана поставок, - выбор метода по поиску решения модели. Другими словами, на практике не всегда удается выбрать алгоритм из известных методов, поэтому требуется разработка авторского инструментария моделирования устойчивых цепочек поставок сырья. При модификации системы ограничений может оказаться, что алгоритм неприменим, и потребуется снова инициировать процесс подборки или разработки алгоритма поиска эффективного решения.

Исходя из вышесказанного цель исследования заключается в разработке метода нахождения эффективного решения проблем класса SCM, сформулированных как задачи стохастического смешанно-целочисленного нелинейного программирования. Для достижения цели поставлены следующие задачи: 1) разработать алгоритм поиска эффективного решения задач класса SCM, являющийся устойчивым с точки зрения неопределенности входных параметров и приемлемым по количеству переменных и времени работы; 2) разработать модификацию модели поставок сырья на примере лесоперерабатывающего предприятия, учитывающую неопределенности и риски сро- ков поставки; 3) сравнить результаты работы авторского алгоритма с известными методами и алгоритмами по поиску оптимального или эффективного решения в задачах формирования устойчивых цепочек поставок сырья лесоперерабатывающего предприятия.

Далее представим краткий обзор алгоритмов и методов по решению задачи формирования устойчивых цепочек поставок сырья.

Обзор методов и моделей решения задач формирования цепочек поставок сырья

В работе [1] показано, что в большинстве рассмотренных исследований  разрабатыва ются модели смешанно-целочисленного линейного программирования  (Mixed- integer Linear Programming, далее MILP) для проектирования и планирования цепочек поставок. Поиск решений в таких моделях осуществляется с использованием коммерческих солверов1. В наше время существует возможность находить оптимальное решение линейных задач большой размерности, но время получения таких решений быстро увеличивается при добавлении целочисленных переменных. Поиск решений для нелинейных моделей еще более сложный и долгий, поскольку, как правило, представляется возможным достигнуть только локального оптимума при условии, что не сохраняются свойства выпуклости. Однако многие нелинейные выражения системы ограничений могут быть линеаризованы (например, в виде кусочно-линейных функций), в том числе за счет ввода дополнительных двоичных переменных.

J.S. Cundiff, N. Dias, H.D. Sherali разработали для системы доставки сырья линейную модель (Linear Programming, далее LP) [2]. Если модифицировать эту LP в двухэтапную задачу, основанную на сценариях, то появится возможность устранить неопределенность уровней производства и погодных условий. С помощью модели с применением сценариев были сведены к минимуму общие затраты, включая затраты на транспортировку, расширение склада, штрафы за нарушение пропускной способности.

Смешанно-целочисленное LP ( Mixed-integer Linear Programming , далее MILP ) используется в случаях, когда ставится задача достичь оптимального распределения объектов. Наиболее распространены однопериодные модели, в то время как большинство реальных процессов производства и / или транспортировки являются многопериодными. Так, в работе [3] разработана модель MILP для размещения складов, промежуточных пунктов хранения между небольшими внутрихозяйственными складами и более крупными централизованными пунктами хранения. Целевая функция состоит из затрат на транспортировку сырья с производственных площадок в централизованный пункт хранения и затрат на пребывание сырья в нем. Авторская модель MILP в работе [4] описывает процесс формирования цепочек поставок сырья. В этой задаче используются пять видов лесного сырья для обеспечения работы установки по пиролизу. Конечная продукция пиролиза может использоваться на месте для производства энергии или отправляться на конверсионную установку для получения бензина и биодизеля. Результатом использования модели явилось оптимальное по максимизации прибыли распределение двух заводов в рассматриваемой области.

Зачастую поиск решений больших моделей рассчитывается в несколько периодов. Y. Huang, C. W. Chen, Y. Fan [5] предложили стратегическую многоступенчатую модель MILP, включающую десять периодов в одном году, для развертывания и настройки мощностей биоперерабатывающих заводов и определения источников сырья для минимизации общих издержек. Задача другой модели MILP [6] - переработать в котлах древесные отходы в производственном районе так, чтобы максимизировать общую прибыль за 52 периода, каждый из которых равен неделе. Имеющиеся или докупаемые котлы могут быть соединены между собой, и их мощность регулируется каждую неделю, чтобы удовлетворить кривые спроса на тепло и электроэнергию. Недавно A. De Meyer, D. Cattrysse, V.O. Jos [7] предложили модель MILP, включающую пять периодов на одногодичном горизонте планирования с учетом временной доступности и регенерации биомассы для определения оптимальных периодов сбора урожая. Модель направлена на оптимизацию чистой прибыли, глобальной эмиссии парниковых газов (Greenhouse Gas, далее GHG) или комбинации этих двух критериев. Это исследование включает в себя анализ чувствительности с учетом неопределенности погодных условий и наличия сырья.

Модели формирования цепочек поставок сырья в рамках MILP могут быть очень большими по количеству как переменных, так и ограничений. Например, одну из таких моделей сформулировал коллектив авторов в работе [8] для определения расположений пунктов отправки конверсионных единиц в 99 округов. Одна итерация - это один месяц работы предприятия. Горизонт планирования составляет 30 лет. Для решения такой задачи требуется 145 000 переменных (в том числе 400 бинарных) и 219 000 ограничений. Цель модели заключается в том, чтобы минимизировать общие годовые затраты, включая транспортировку биомассы, конверсию и транспортировку биотоплива, а также стоимость сырья и штрафы, вызванные его нехваткой.

Нелинейные модели находят применение в производстве и проектировании сетей. M. Bruglieri и L. Liberti [9] разработали сложную модель по формированию цепочек поставок биосырья, в которой ведется учет местоположения энергетических установок, производственных мощностей и весов дуг в сети для минимизации суммарных затрат. В модели учитываются транспортные расходы, производственные затраты и затраты на поставку товаров. Модель сформулирована как задача смешанно-целочисленного нелинейного программирования ( MINLP ), небольшие части которой могут быть решены с помощью специальной процедуры ветвления с гарантией сходимости к оптимуму. Модель

MINLP также приводится в [10] и посвящена оптимальному проектированию цепочки поставок сырья для минимизации общих ежегодных затрат и общих годовых выбросов GHG . Shabani переформулировал модель многопериодного нелинейного программирования ( Multi-period Nonlinear Programming , далее MPNP ) для оптимизации цепочек поставок лесного биотоплива в виде модели линейного программирования, где целевая функция направлена на максимизацию показателя суммарной прибыли. Разработанная модель впоследствии расширяется до двухэтапной стохастической модели LP для учета неопределенности возникновения у поставщиков некоторого объема сырья [11].

Если прямое решение математической модели коммерческим солвером занимает слишком много времени, можно использовать эвристику [12]. Эвристические алгоритмы позволяют за приемлемое и более короткое, чем точные алгоритмы, время находить некоторое решение задачи, но эвристические методы не дают гарантий оптимальности [13]. Существуют исследования в области формирования цепочек поставок сырья, оперирующие метаэвристикой и семейством эвристик, в которых реализованы различные механизмы, позволяющие избегать попадания решения в локальный оптимум [14]. В отличие от математических моделей, которые могут быть быстро реализованы с использованием специальных языков, близких к математическому синтаксису, метаэвристика должна быть адаптирована к рассматриваемой проблеме и реализована на низкоуровневом языке программирования [15].

Методика поиска решения с использованием модификаций генетического алгоритма ( Genetic Algorithms , далее GA ) заключается в выполнении повторяющейся последовательности операций размножения (многократное копирование полученного на прошлом шаге решения¹), мутации

(случайные изменения каких-либо элементов каждого размноженного решения), селекции (отбор допустимых решений, которые доставляют лучшее значение целевой функции) подобно тому, как эти процессы протекают у живых организмов в природе [16–18]. H.D. Venema и P.H . Calamai [16] применяют эту схему для поиска оптимального расположения объектов в сельском регионе. Задача состоит в том, чтобы минимизировать общие транспортные расходы, которые вычисляются как скалярное произведение вектора спроса на вектор расстояний и приводят к модифицированной задаче о p -медиане. Одна из модификаций GA разработана учеными N. Ayoub и N . Yuji [17]. Они описывают гибкую структуру для моделирования строительной сети ( B-NET ) – сложных цепочек поставок сырья. B-NET определяется авторами как группа зависимых и взаимосвязанных процессов, использующих один или несколько типов ресурсов, что приводит к производству одного или нескольких видов продукции. Оптимизация цепочки поставок может быть выполнена путем решения MILP , полученной из B-NET . Если же размерность задачи достаточно велика, то в этом случае авторами заложена возможность ее решения посредством использования GA за заданное время.

Сразу в двух работах [18; 19] рассматриваются подходы к энергоснабжению жилых помещений с использованием нескольких видов сырья, а также электричества, отопления и охлаждения. Их особенностью является игнорирование сегментов производства и транспортировки сырья: предполагается, что любое количество может быть приобретено по известной цене. Для удовлетворения потребностей в энергии при максимизации чистой приведенной стоимости были предложены нелинейные модели. Поскольку поиск решений в моделях нелинейного программирования является вычислительно сложным, то для вычисления начального допустимого решения была разработана модификация генетического алгоритма. В работе изложена модификация генетического алгоритма путем его скрещивания с мето- дом последовательного квадратичного программирования (SQP) для поиска оптимального решения.

Метаэвристика, основанная на роевом интеллекте¹, также ставит своей целью поиск решений, но подчиняется другим принципам. Подобно поведению косяков рыб и стай птиц, они основаны на поисковых агентах, которые перемещаются в пространстве решений и «сотрудничают», чтобы найти наилучшие. В работе [20] выбрана «оптимизация роя бинарных частиц» ( BPSO ), чтобы найти и подключить электростанции, работающие на лесном биотопливе, в сельской местности. BPSO используется для максимизации прибыли при нелинейных ограничениях, таких как профили напряжения. По сравнению с генетическим алгоритмом он показывает более быструю конвергенцию, и с его применением, как утверждают авторы, можно получить лучшие решения [22]. Другой алгоритм на основе роевого интеллекта, Binary Honey Bee Foraging ( BHBF ), представлен в работе [23] и применяется к аналогичной проблеме, в которой сырье состоит из остатков оливковых деревьев. BHBF превосходит BPSO и GA (две предыдущие работы) в некоторых случаях.

В недавнем исследовании [24] эвристический подход, основанный на структуре адаптивного поиска большого соседства ( ALNS ), применяется для решения проблемы выбора поставщика и планирования закупок для биоэлектростанции с учетом временных окон и ограничений по уровню запасов сырья.

К категории подходов, относящихся к гибридным методам, которые сочетают процедуры точного решения с эвристикой или метаэвристикой, можно отнести работу M. Marufuzzaman, S.D. Eksioglu, Y. Huang [25], в которой предложен синтез инструментов лагранжевой релаксации и L-образного алгоритма для решения двухэтапной стохастической смешанноцелочисленной модели линейного программирования, которая позволяет проектировать цепи поставок сырья и управлять ими. M.S. Roni, S.D. Eksioglu, E. Searcy, K. Jha [26] разработана модель проектирования цепочек поставок биомассы для ее сжигания на угольных электростанциях. В качестве алгоритма поиска решения использовался GA. Целевая функция направлена на минимизацию общих расходов на транспортировку и штрафы.

Проведенный обзор показывает отсутствие единого мнения и подхода к решению задач класса SCM. Актуальной проблемой поиска решения задач формирования устойчивых цепочек поставок сырья большой размерности является отсутствие алгоритма, который был бы приемлемым по времени работы и гибким с точки зрения возможности его применения к различным по степени включенности стохастическим параметрам.

Далее представлен авторский подход к решению этой задачи.

Математическая модель формирования устойчивых цепочек поставок сырья с учетом вероятностного характера параметров доставки

Модель по формированию устойчивых цепочек по ставок сырья на склад предложена в работе2, однако в ней не учитываются риски, связанные с неопределенностью выполнения поставщиками договорных обязательств по качеству сырья и времени доставки. Модель ориентирована на поиск оптимального3 или эффек-тивного4 решения задачи формирования цепочек поставок сырья из регионов на основе работы с товарно-сырьевой биржей России с учетом ежедневной нормы потребления сырья предприятием. Особенность работы данного сектора биржи за- ключается в том, что лот можно купить только целиком1.

Введем следующие обозначения:

M - рассматриваемый горизонт планирования (дни), называемый текущим периодом;

M - дополнительный период, который наступает после M. В этот период покупки не рассматриваются, но необходимо спланировать закупки на горизонте M так, чтобы и в этот период была возможность производственной деятельности;

I - количество заявок, которые были куплены в предыдущий период (до т = 0) и поступят на склад уже на горизонте [0, M];

R - количество регионов, откуда поступают предложения по продаже;

С [ _Г - цена покупки i -й заявки в r-м регионе (руб.), включая стоимость доставки;

• V tr - объем сырья в заявке i из региона г (м³);

• V [ _r - объем сырья в заявке i из региона г, купленной в предыдущий период ( м³ );

• ^si _r m - расстояние, пройденное заявкой i из региона г в день т в текущем периоде (км);

^ i _rm - расстояние, пройденное заявкой i из региона г в день т в дополнительном периоде (км);

и_т - запас сырья на складе в день т (м³);

_и ^т ах - максимальная вместимость склада (м³);

_u ^mi n - неприкосновенный запас сырья на складе ( м³ );

L_r - расстояние от региона г до склада по железной дороге (км);

и - количество сырья, потребляемого производством каждый день ( м³ );

' - случайна я величина непрерывного типа, имеющая нормальное распределение ^(Ж,D'), где Ж - математическое ожидание, D - дисперсия.

Математическая модель F имеет вид

У C ir   max . (A irm ) ^ min, i—l   m = 1:M+M	(1)
i,r
ит+1 — ит  и + ^ (Airm1  Air(m-1)1' )'^ ir +
i,r
+ ^ i,r ( Airm1   Air(m-1)1 )^ ir ,	(2)
ит< итах,т — 1: M + M ,	(3)
ит > иmin,т — 1: M + M ,	(4)
(1, если куплена заявка i в регионе г yirm — )   ко дню т в текущем периоде 0,иначе ( 1, если куплена заявка i в регионе г yirm — ) ко дню т в предыдущий период 0, иначе	(5)
	(6)
и0 — const,	(7)
1, если купленная в текущем Airm1 — \ периоде заявка i в регионе г доставлена ко дню т 0, иначе	(8)
1, если купленная в прошедшем Airm1 — { периоде заявка i в регионе г { доставлена ко дню т 0, иначе	(9)
Airm1Lr + Airm2sirm   sir(m-1) + +yirm * (' - tirm) , Airm1Lr + Airm2sirm — sir(m-1) +	(10)
+yirm * (' - t irm ),	(11)
Airm1 + A irm2    1 ,	(12)
Airm1 + A irm2 — 1 ,	(13)
tirm   Airm1((sirm + ') — Lr ) >  0 ,	(14)
f irm   Airm1((sirm + ') — Lr ) > 0 ,	(15)
0 <  sirm <  (Lr — 10 17 )yi.rm ,	(16)
0 <  sirm <  (Lr — 10 17 )yirm ,	(17)
yirm >  Airm1 ,	(18)
yirm >  Airm1 ,	(19)
Airm2 , Airm2 ^ {0 , 1} ,	(20)
Airm1 >  Air(m-1)1 ,	(21)
Airm1 >  Air(m-1)1 ,	(22)
yirm >  yir(m-1) ,	(23)
yirm >  yir(m-1) ,	(24)
sir0    0 ,	(25)
sir0 — const.	(26)

Рассмотрим модель (1–26) подробнее. Целевая функция в (1) равна суммарному объему затраченных средств на за- купку сырья на заданном горизонте планирования. Рекуррентная зависимость (2) задает для каждого дня количество сырья на складе, (3) и (4) ограничивают сверху и снизу соответственно объем сырья на складе, (5) и (6) отражают то, какие значения принимают переменные в текущем периоде в зависимости от принятых решений по покупке заявок в текущем и прошлом периоде планирования соответственно. (7) – начальные запасы сырья на складе. (8) и (9) отражают факт доставки сырья i-й заявки на склад в зависимости от периода, когда та была куплена. (10) и (11) – рекуррентные зависимости пройденного грузом расстояния, если тот был куплен. (12) и (13) описывают то, что товар может быть либо в пути, либо на складе. В случае если груз достиг пункта назначения, предусмотрены ограничения (14) и (15), чтобы значение пройденного заявкой расстояния S[rm или Sirm не росло. Ограничения (16) и (17) задают промежуток изменения, пройденного купленной заявкой расстояния.

Кроме того, (16) и (17) предназначены для случая: груз прошел расстояние ( и S ir(m-1) + t = S irm = ^Lr , то есть по (10), (11) он придет в день (т + 1), но на самом деле он пришел в день т. С целью исключения этого крайне маловероятного, но возможного события в ограничениях (16) и (17) вычитается малое число 10^-17.

Пара ограничений (18) и (19) формализует следующее: если заявка не была куплена, то она не может быть доставлена. Ограничения (21) и (22) –формализация утверждения: если заявка не прибыла на склад до момента m , то она и не прибыла до момента ( m– 1), и наоборот: если она пришла в текущий момент, то в следующий момент она тоже будет считаться доставленной. Аналогичная логика относительно переменных y i _rm,y i _rm в ограничениях (23) и (24). (25) задает стартовое значение пройденного расстояния заявкой, купленной в текущем периоде М, а (26) -суммарное пройденное заявкой расстояние в «прошедшем» периоде.

В модели случайной величиной является значение пройденного расстояния ( в любой день на горизонтах планирования М и М . Переменными оптимизации выступают y i _rm , задающие включение заявки в портфель. Таким образом, построенная модель F относится к классу стохастического нелинейного целочисленного программирования.

Входные данные модели задаются на основе анализа потока предложений на официальном сайте Санкт-Петербургской Международной Товарно-сырьевой Бир-жи1. В качестве предприятия выбрана одна из крупных лесопромышленных компаний Приморского края. На момент начала поиска оптимального решения у предприятия находится некоторый начальный объем сырья.

Поиск эффективного решения разделим на два этапа – поиск допустимого решения ( Алгоритм А) и поиск эффективного решения путем улучшения допустимого ( Алгоритм В).

Алгоритм А представляет собой последовательное построение дерева решений по дням, и для каждого дня выбирается минимальная по стоимости заявок ² комбинация. Однако для каждого дня, кратного значению³ Ik, случайно будет выбираться комбинация заявок. Этот шаг направлен на более быстрое нахождение первого допустимого решения, так как классический метод ветвей и границ очень долго ищет первое допустимое решение. Если на каком-то шаге уровень запаса сырья упал ниже u^min , то предстоит вычеркнуть из рассмотрения текущую комбинацию заявок и перейти к следующей по стоимости. Если в текущий день множество комбинаций заявок пусто и выбирать не из чего, то перейти на предыдущий шаг и изменить по этому же правилу решение⁴. Как только будет найдено первое допустимое решение, алгоритм заканчивает работу.

Алгоритм В заключается в последовательном выполнении шагов по тестированию полученного решения на предмет его устойчивости1 (Шаг 3B), по размножению и случайной мутации (Шаг 4B), по селекции (Шаги 5B–7B), по направленной модификации (Шаг 8B), по селекции (Шаг 9B) и по изучению сложившейся ситуации для остановки алгоритма (Шаги 10B–11В).

Рассмотрим некоторые шаги Алгоритма В подробнее. Шаг 4B заключается в классическом размножении полученного решения, а затем в мутации. Процесс мутации заключается в удалении текущей комбинации заявок из решения и замене ее на более дорогую комбинацию заявок² с последующим вызовом Алгоритма А для поиска допустимого решения. После отбора лучшего полученного решения по стоимости на Шагах 5B – 7B предстоит провести модификацию этого решения на Шаге 8B . Любое новое полученное решение необходимо тестировать на предмет его допустимости ( Шаг 9B ). Если оно недопустимо, необходимо его отправить на доработку до допустимого ( Алгоритм А). Если за какое-то время или количество итераций не получается отыскать решение, лучше найденного, то закончить алгоритм.

Рассмотрим подробнее алгоритмы А и В. Будем искать решения на интервале издержек Т С(1 + d), где А - значение разброса (в процентах от значения минимальных издержек одного из решений ТС). Зададим некоторое значение к.

Алгоритм А по поиску допустимого решения модели F:

Шаг 1A³: Задаем начальные данные:

т = 1, ТС = ж,nodes = nodes. Перейти к шагу 2 A.

Шаг 2A: Строим дерево решений для т -го дня. Строим все возможные деревья для этого дня⁴. Перейти к шагу 3A.

Шаг 3A: Ранжируем деревья решений по стоимости. Перейти к шагу 4 A.

Шаг 4A: Если множество решений для т-го дня равно 0 и т = 1, то выйти из алгоритма.

Если множество решений для т-го дня равно 0, тогда т = т — 1 5 и текущее решение из (т — 1)-го дня тоже вычеркиваем и переходим к шагу 3A. Забыть все метки с y_irm в дни, следующие за днем (т — 1).

Если множество решений для т-го дня не равно 0 и тоС(т, к) Ф 0 6 , то выбираем самое дешевое из имеющихся. Перейти к шагу 5 A.

Если множество решений для т-го дня не равно 0 и тоС(т,к) = 0, то выбираем случайное из имеющихся. Перейти к шагу 5 A.

Шаг 5A: Проверяем выполнение всех ограничений модели F для построенного вектора закупок.

Если при использовании алгоритма было рассмотрено nodes комбинаций решений, и не было найдено допустимых решений, и запуск Алгоритма А не первый, то осуществляется выход из алгоритма (должны выполняться все три условия).

Если производство начало простаивать (не выполнилось (4)), вычеркиваем это решение из дерева решений, полученного на шаге 4 A , и переходим к шагу 4 A без этого решения для дальнейшего ветвления.

Если значение издержек на этом шаге выше, чем значение ТС, вычеркиваем это решение из дерева решений из шага 4 A и переходим к шагу 4 A без этого решения для дальнейшего ветвления.

Если производство не простаивает, значение текущих издержек меньше ТС и текущий рассмотренный день т не является последним, то принять т = т + 1 и перейти к шагу 2 A.

Если производство не простаивает, значение текущих издержек меньше ТС и текущий рассмотренный день т является последним, то сохранить данное решение в векторе X, записать показатель ТС, вычеркнуть полученное решение в текущем дне из дерева решений. Выход из алгоритма.

Конец алгоритма.

Рассмотрим Алгоритм В по поиску решения модели F с применением методики параллельного программирования для шагов 2В–4В и 9В:

Шаг 1B: Задаем начальные данные: т = 1, ТС = ^[ ^],D,k = k:,s = 1,{L_irm} = = 0,9 = 9%, {L} = 0, iter = iter, а = = а%,т 1 = m 1 ,m₂ = m 2 ,9 = 9. Перейти к шагу 2B.

Шаг 2B: Получить первое допустимое решение ( Алгоритм Л). Перейти к шагу 3B.

Шаг 3B: Подставить полученное решение iter раз в систему (1-28) и замерить количество случаев, когда предприятие не останавливалось (4).

Если отношение количества случаев, когда предприятие не останавливалось, к iter не превосходит а, то добавить решение в таблицу на шаге 5B. Перейти к шагу 4B с текущим решением.

Если отношение количества случаев, когда предприятие не останавливалось, к iter превосходит а, то продолжаем искать допустимое решение (шаг 2В) – продолжить процесс ветвления.

Шаг 4B : Полученное решение размножить на m 1 + m 2 * X i _rm L [ _rm структурно одинаковых решений. Случайно изменить каждое из m 1 + m 2 * S i _rmL ; _rm решений следующим образом: изменить в любой день ребро (взять в этот день большую по стоимости заявку). Удалить остатки, идущие после этого дня, от прошлого решения. Использовать Алгоритм Л для поиска допустимого решения или перебрать nodes комбинаций решений. Перейти к шагу 5B.

Шаг 5B: Дождаться выполнения всех остальных операций из Алгоритма В. Сформировать матрицу (N, X_m TC_mN,

^irm Virm, ^N(устойчивости)1, {yirm}N), PN(устойчивости)2, {yirm^N), где N - номер решения, ^mTCmN - суммарные издержки на закупку сырья в решении N, Xirm Virm - суммарный объем закупленного сырья, PN(устойчивости') - вероят ность устойчивости решения N, {yirm}N -набор заявок в решении N. Добавить в матрицу в качестве строк решения из множества {L}. Перейти к шагу 6B.

Шаг 6B: Сортировка матрицы по значениям в столбце Z_m TC_mN по убыванию.

В случае если попадутся одинаковые значения Y,_mTC_mN , сортировать эти элементы по столбцу P_N(устойчивости') по убыванию. Перейти к шагу 7 B.

Шаг 7B: Формируем вектор относительных встреч: записываем в матрицу М строки с допустимыми решениями из шага 6B. Сравниваем ТС и ^_mTC_m1 первого решения из таблицы.

Если выполняется условие

ТС(1 +9) < ^_mTC_m1 , перейти к шагу 8B.

Если выполняется условие

ТС(1 — 9) > 'L_mTC_m1, полагаем

ТС = X_m TC_m1 и обновляем {L} текущим решением, отправляем решение на шаг 4 B.

Если значение ^_mTC_m1 попадает в диапазон ТС(1 ±9), дополнить {L} текущим решением, перейти к шагу 8B.

Шаг 8B: Дождаться выполнения всех остальных операций. Рассчитать значения элементов трехмерного массива М , где Mi irm = ®^Ш. Выделим ядро

^N max

Lirm = {Mirm,если Mirm = 1. Рассчитаем (     0, иначе значение элементов псевдоядра

1, если M_irm > к 0,иначе ^.

^Lirm =   = {

Если к + ^s/iqqq >  1, перейти к шагу 11B.

Если   EirrnUirrn} = 0^ к = к/2, перейти заново к шагу 8B.

Если E i _rm{L i _r m } ^ 0 ^ к = к, перейти к шагу 9B.

Шаг 9B: s = s + 1. Прогнать {L_irm} iter раз. Производство останавливалось более а% раз?

Если да, перейти к шагу 2B.

Если нет, то сравнить значения ТС и суммарных издержек Е_т ТС_т для решения, полученного на шаге 8В:

если выполняется условие

ТС(1+т9) <  Е_тТС_т , то отправить решение к шагу 3B;

если выполняется условие

ТС(1-д) > Е_тТС_т , то перезаписать ТС = Е_т ТС_т и обновить {L] текущим решением, перейти к шагу 10B.

Если значение попадает в интервал

Шаг 10B:

Если значение ТС после попадания на этот шаг не менялось в раз подряд, то выйти из алгоритма и решением (решениями) является массив {L}.

Если менялось, то перейти к шагу 5B.

Шаг 11B: выйти из алгоритма, и массив {L} есть решение (решения)¹ задачи. Конец алгоритма.

Далее представлены результаты калибровки модели и анализ эффективности работы авторского алгоритма.

Калибровка параметров модели и анализ результатов работы алгоритма

Зададим входные значения. Часть из них приведена в табл. 1. Алгоритму предстоит работать с опубликованными данными биржи. Рассмотрим три разных периода

М: с 1 февраля по 31 июня 2017 г. (150 дней), с 1 февраля 2017 г. по 1 февраля 2018 г. (365 дней), с 1 февраля 2017 г. по 15 мая 2019 г. (« 800 дней). За весь временной интервал в торгах участвовали Ир- кутская область (г = 1), Республика Удмуртия (г = 2), Московская область (г = 3) и Пермский край (г = 4). За рассматриваемые периоды было 212, 759, 1665 заявок соответственно. В качестве скользящего периода планирования М был взят временной интервал в 1 месяц. Производство расположено в г. Спасск-Дальний, Приморский край, Россия.

Таблица 1. Входные данные для решения тестовой задачи по формированию устойчивых цепочек поставок сырья

Table 1. Input data for a test supply chain management problem

№	Параметры*	Значение
1	итах , м3	7500
2	ит1п , м3	100
3	~   3 и , м	183
4	Lr , км	[3242, 7232, 8200, 7892]
5	М , месяц	М
6	к , км	~N(1050,2502) **
7	к , день	4
8	3 U q , м	6500
9	d ,%	5
10	nodes , ед.	1024
11	■ к	0,8
12	iter , ед.	100
13	а , %	5
14	т1	5
15	т2	10
16	в , ед.	3

* Параметры (1–4) задаются предприятием, (5–16) – авторами.

** 1050 км – математическое ожидание, 250² км - дисперсия.

Считаем, что на начало работы алгоритма поток V [ _r представляет собой 2 заявки суммарным объемом 143 м³, следующие из Иркутской области. Кроме того, отметим, что бюджет предприятия не ограничен.

Поясним пункт 5 табл. 1. Алгоритм будет работать из расчета на два месяца планирования, но лишь первый месяц будет записан в вектор решения. Каждый месяц алгоритм будет запускаться заново со сдвигом на один месяц для учета следующих двух месяцев. Так планируется учитывать тенденцию изменения наличия сырья на бирже в каждый отдельный месяц.

Максимальное время поиска решения составляет 3 ч.

Оценка эффективности работы авторского алгоритма (далее АА) проведена сравнением с методом ветвей и границ (далее МВиГ) [1–3] и генетическим алгоритмом (далее ГА) [4; 5; 15]. Были выбраны 4 разных процессора (табл. 2). Оперативная память компьютера 16 Гб. Для реализации процесса распараллеливания использовался аппарат MPI1, встроенный в Matlab.

В табл. 2 приведены значения лучшего решения для каждого алгоритма. Для адекватности оценки эффективности работы АА и ГА каждый был запущен по 25 раз для каждого значения горизонта планирования.

Таблица 2. Сравнение результатов работы алгоритмов*

Table 2. Comparison of the algorithms’ results

Критерий эффективности работы алгоритма	Алгоритм	Горизонт планирования, дней	Пр (яд	оцессоры и их характеристики а – потоки, шт., частота – ГГц)
			AMD Ryzen 9 3950X BOX (16 (32), 3.5)	AMD Ryzen 7 3700X BOX (8 (16), 3.2)	AMD Ryzen 5 3600 BOX (6 (12), 3.2)	AMD Athlon 240GE OEM (2 (4), 2.7)
Значение    целевой функции, млн руб.	МВиГ	150	1,45	1,61	2,22	3,01
		365	NaN**	NaN	NaN	NaN
		800	NaN	NaN	NaN	NaN
	АА	150	1,62	2,11	2,32	3,53
		365	4,62	4,89	5,29	9,82
		800	9,81	11,21	15,72	18,49
	ГА	150	2,1	2,31	2,56	3,67
		365	4,98	6,21	7,32	10,19
		800	11,02	12,31	18,99	21,39
Количество изменений эффективного решения, раз	МВиГ	150	12	8	7	2
		365	NaN	NaN	NaN	NaN
		800	NaN	NaN	NaN	NaN
	АА	150	13	12	10	2
		365	15	13	13	2
		800	17	18	17	2
	ГА	150	6	19	2	1
		365	18	12	19	2
		800	27	11	20	3
Время работы алгоритма до срабатывания критерия остановки, мин	МВиГ	150	180	180	180	180
		365	180	180	180	180
		800	180	180	180	180
	АА	150	128,21	151,98	179,12	180
		365	178,32	180	180	180
		800	180	180	180	180
	ГА	150	180	180	180	180
		365	180	180	180	180
		800	180	180	180	180

* В таблице округление некоторых значений проводится до второго знака после запятой; ** NaN – нет значения.

Сост.1по источнику: AMD Ryazon. Processors. URL: (дата обращения: 01.02.2020).

Элементы табл. 2 и рис. 1–3 отражают показатели найденного лучшего решения из 25 реализаций алгоритма с одинаковыми начальными данными. При реализации МВиГ было получено решение для горизонта планирования в 150 дней. Однако на бóльших горизонтах планирования этот алгоритм показал себя слабоэффективным, в то время как АА и ГА показали себя лучше, и в процессе их работы удалось отыскать эффективные решения.

Рассмотрим количество изменений вектора закупок при нахождении эффективного решения. АА показал себя с лучшей стороны относительно МВиГ, потому что в процессе работы алгоритма удалось отыскать больше допустимых решений, а последнее означает, что на более сложных задачах в процессе его работы можно перебрать больше промежуточных решений, что скажется на качестве конечного эффективного решения. При рассмотрении результатов работы пары алгоритмов ГА и АА в разрезе любого горизонта планирования стоит отметить, что ГА является более нестабильным по количеству изменений вектора закупок в зависимости от типа процессора и горизонта планирования.

Рассмотрим время работы алгоритмов. Из всех трех алгоритмов лишь АА выходил из цикла раньше. Более того, результаты его работы были лучше, чем у ГА, однако хуже, чем у МВиГ. Последнее объясняется тем, что МВиГ – это алгоритм, который сходится к оптимальному решению [11]1, в то время как у ГА [1–3] и АА нет таких гарантий.

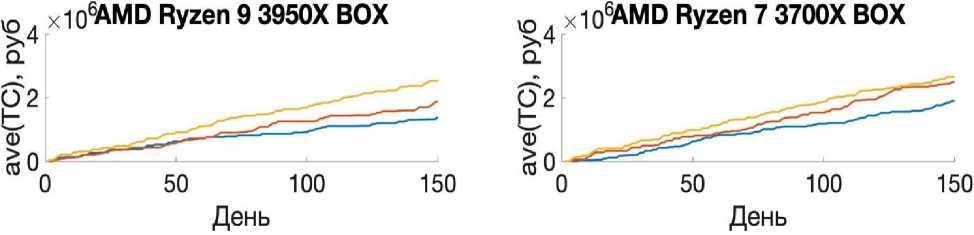
Рис.¹1.1 .

Рис. 1.2

— МВиГ

—АА

ГА

Рис. 1.3.                                          Рис. 1.4

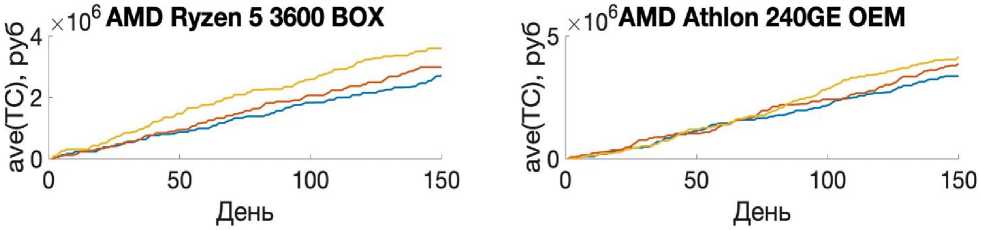
Рис. 1. Визуализация поведения накопленных издержек для горизонта планирования в 150 дней

Fig. 1. Visualization of accumulated costs behavior for a 150-day planning horizon

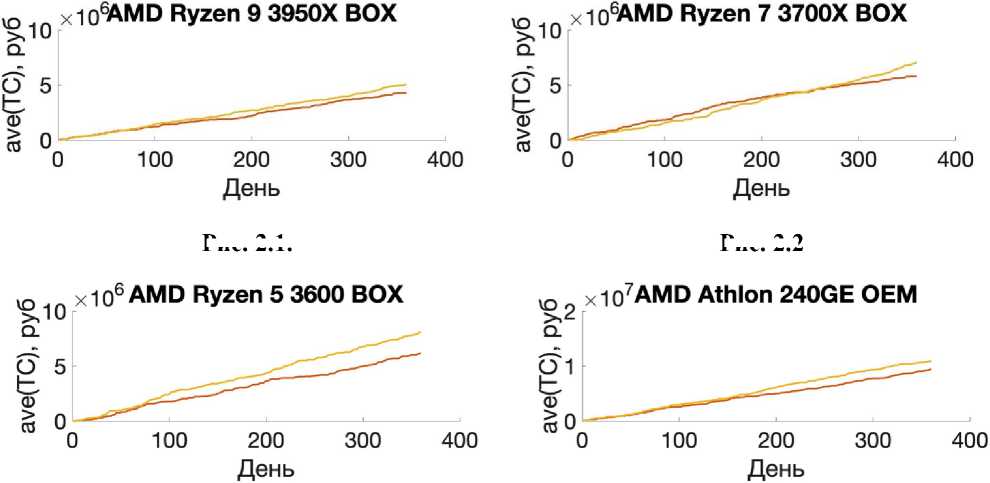
Рис. 2.1.

Рис. 2.2

Рис. 2.3.

— МВиГ

- АА

ГА

Рис. 2.4

Рис. 2. Визуализация поведения накопленных издержек для горизонта планирования в 365 дней

Fig. 2. Visualization of accumulated costs behavior for a 365-day planning horizon

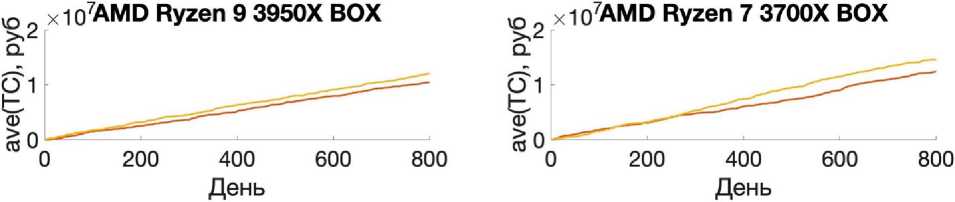
Рис. 3.1.

Рис. 3.2

—МВиГ

—АА

ГА

Рис. 3.3.                                        Рис. 3.4

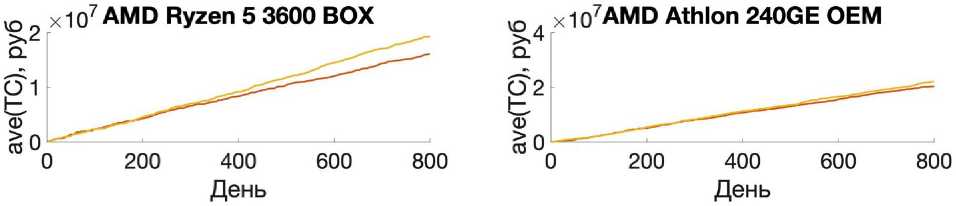
Рис. 3. Визуализация поведения накопленных издержек для горизонта планирования в 800 дней

Fig. 3. Visualization of accumulated costs behavior for an 800-day planning horizon

На рис. 1–3 изображена динамика величины издержек для разных алгоритмов, горизонтов планирования и процессоров. Для определенности будем вести нумерацию подрисунков с верхнего левого угла, слева направо последовательно.

На рис. 1 видно, что в краткосрочной перспективе планирования (150 дней), как и было отмечено ранее, по конечному значению целевой функции лидирует МВиГ, при этом на рис. 1.4 есть промежуток, когда АА находит решение с меньшим значением издержек. Меньшее значение издержек на интервале достигается лишь в краткосрочной перспективе в то время, как в долгосрочном периоде МВиГ показывает меньшее значение конечных издержек.

Исходя из рис. 1.2 можно сделать вывод, что ГА и АА ведут себя примерно одинаково. Это связано с тем, что эти два алгоритма плохо себя показывают на небольших выборках, так как АА основан на скрещивании ГА и МВиГ, а, в свою очередь, ГА, как известно, не является эффективным на такой размерности выборок [1– 3]. Не исключено, что при увеличении числа входных параметров и/или периода планирования ГА и АА продемонстрируют лучшие результаты.

Последнее предположение отчетливо отражается на рис. 2 и 3. На этих рисунках видно, что МВиГ не показал видимых результатов в то время, как удалось отыскать решение задачи с применением алгоритмов АА и ГА. На рис. 2.2 так же, как и на рис. 1.2, можно увидеть, что существует интервал, на котором ГА показывает себя лучше, однако в конечном итоге АА отыскивает решение по стоимости ниже.

По данным рис. 2 и 3 результаты работы АА лучше, чем ГА.

Рассмотрим перспективы развития предложенной модели и алгоритма.

Одной из главных проблем лесопромышленного производства является своевременность доставки сырья на склад. В противном случае покупатель имеет право отказаться от сырья и потребовать ком- пенсацию1. Но такой сценарий не является однозначно приемлемым ни для продавца сырья, ни для покупателя. Последнему это невыгодно, потому что предприятие будет простаивать и придется искать сырье по более высокой цене в кратчайшие сроки в малой окрестности пункта производства. Поэтому желательно ввести функцию вероятности отказа от заявки по факту невыполнения договора в части срока доставки и изменения качества сырья.

Кроме того, предприятие не каждый день использует одинаковое количество сырья. Это связано с несколькими факторами – структурой и объемами выпуска продукции каждого вида в динамике, типом используемого сырья и нормами ресурсозатрат на каждый вид выпускаемой продукции. В совокупности эти факторы могут значительно влиять на необходимый суточный объем сырья, поэтому имеет смысл добавить в модель зависимости, связанные с учетом выпуска различных видов продукции.

Наряду с закупками сырья предприятия лесопромышленной отрасли в основном сами занимаются транспортировкой конечного вида продукции до покупателя. Поэтому желательно выстраивать модель, объединяющую три подпроцесса и позволяющую комплексно находить оптимальные планы закупки сырья, объемов выпуска продукции и путей доставки ее до конечного потребителя.

Следовательно, модернизация алгоритма возможна по следующим направлениям:

• а)    в случае если удастся, исходя из практики транспортировки сырья, заменить серию ограничений с пройденным расстоянием на общее время в пути, то поиск допустимого решения ( Алгоритм А) можно заменить на задачу линейного программирования, что, несомненно, позволит уменьшить время поиска эффективного / оптимального решения;

• б)    доказать выпуклость допустимого множества решений, что даст возможность подобрать точный алгоритм поиска оптимального решения в некоторой окрестности.

Отметим, что авторский алгоритм имеет достаточно широкое применение, так как с его использованием можно решать различные стохастические SCM и нестохастические модификации данного класса задач большой размерности.

Заключение

Задача формирования устойчивых цепочек поставок сырья является базовой проблемой для любого предприятия. Отсутствие еди- ного подхода к решению такого рода задач открывает широкие возможности по построению алгоритмов и моделей. В работе предложен базовый алгоритм, позволяющий находить эффективное решение некоторого класса задач стохастического нелинейного программирования. Алгоритм относится к классу эвристических и на отдельных шагах использует метод ветвей и границ и генетический алгоритм. Тестирование алгоритма показало хорошую результативность его работы на больших выборках с точки зрения затрачиваемого времени с использованием относительно немощных процессоров, например AMD Ryzen 5 3600 BOX и AMD Athlon 240GE OEM. На четырех видах процессоров, включая и более производительные (AMD Ryzen 9 3950X BOX и AMD Ryzen 7 3700X BOX), для различных вариантов модели функционирования поставок технологического сырья для промышленного предприятия проведено сравнение алгоритма с отдельным применением генетического алгоритма и метода ветвей и границ. Алгоритм является более устойчивым с точки зрения неопределенности входных параметров по сравнению с генетическим и в отличие от метода ветвей и границ позволяет успешно находить эффективные решения моделей со значительно большим количеством переменных. Универсальность алгоритма для рассматриваемого класса задач позволяет при необходимой модификации расширить возможность его применения к большему количеству веро- ятностных параметров, описывающих неопределенности процесса поставок сырья.

Разработанный алгоритм используется при моделировании процесса по формированию устойчивых цепочек поставок сырья на производственные предприятия с учетом неопределенности. Модель представляет собой задачу смешанно-целочисленного нелинейного программирования, целевой функцией которой является величина суммарных затрат на закупку сырья на товарно-сырьевой бирже на заданном горизонте планирования. Решением модели является план закупок сырья, обеспечивающего технологические потребности лесоперерабатывающего предприятия. Неопределенности и риски, связанные с отклонениями от договорного времени поставки, моделируются представлением некоторых параметров в виде случайных величин. Оптимизация проводится по бинарным переменным, характеризующим включенность той или иной заявки в план закупок. Апробация работы алгоритма и применение модели проведены на одном из крупных лесоперерабатывающих предприятий Приморского края.

Рассмотрены возможности по модификации математической модели и разработанного алгоритма. Отмечено, что если преобразовать алгоритм так, чтобы были гарантии его сходимости, то алгоритм станет более эффективным. В качестве одной из главных характерных черт лесопромышленной отрасли является вероятность отказа от сырья, если оно слишком долго находится в пути. Отмечено, что представленную модель можно модифицировать для учета этого важного для отрасли риска. Кроме того, имеет смысл добавить в модель форму учета норм затрат сырья на производство каждой единицы продукции, что скажется на ежедневных потребляемых объемах сырья на предприятии и тем самым изменит структуру вектора закупок сырья на каждый день. Также имеет значение добавление в модель аналога транспортной задачи по доставке конечной продукции до потребителя, что существенно расширяет границы ее применения.

В части разработки алгоритма нахождения решения задачи стохастической нелинейной оптимизации работа выполнена при финансовой поддержке Российского фонда фундаментальных исследований в рамках научного проекта № 18-010-01010.