Алгоритм интегрирования переменной конфигурации на основе явно-неявных схем четвертого порядка

Во многих важных приложениях возникает проблема численного решения задачи Коши для обыкновенных дифференциальных уравнений. В современных методах решения жестких задач при вычислении стадий применяется /.//-разложение матрицы Якоби. В случае достаточно большой размерности исходной системы быстродействие алгоритма интегрирования фактически полностью определяется временем декомпозиции этой матрицы. Для повышения эффективности расчетов в ряде алгоритмов используется замораживание матрицы Якоби, то есть применение одной матрицы на нескольких шагах интегрирования [1]. Наиболее успешно этот подход применяется в многошаговых методах [2]. Не вызывает эта проблема особых трудностей и при построении алгоритмов интегрирования на основе других численных схем, если в них стадии вычисляются с участием матрицы Якоби в некотором итерационном процессе. В алгоритмах интегрирования на основе известных безытерационных численных схем, к которым относятся методы типа Розенброка [3] и их различные модификации [1], проблема замораживания более трудная. Следует отметить, что с точки зрения реализации безытерационные методы существенно проще алгоритмов на основе численных формул, в которых стадии вычисляются с применением итераций. Некоторым аналогом замораживания матрицы Якоби является применение в расчетах алгоритмов интегрирования на основе явных и А-устойчивых методов с автоматическим выбором численной схемы. В этом случае эффективность алгоритма может быть повышена за счет расчета переходных участков явным методом [4]. В качестве критерия выбора эффективной численной формулы естественно применять неравенство для контроля устойчивости [5].

Здесь на основе L-устойчивого (4,2)-метода и схемы Мерсона четвертого порядка точности построен алгоритм переменной структуры. Приведены результаты расчетов задачи проникновения помеченных радиоактивной меткой антител в пораженную опухолью ткань живого организма.

1.    Исследование (4,2)-метода

Рассмотрим задачу Коши вида

У = ДуУ УШ = УоДо ^^k,               W где у и f — вещественные /V-мерные вектор-функции, / — независимая переменная. Для решения задачи (1) рассмотрим численную формулу [6]

УпА=Уп*РУкАЛ--*РУк© Dn=E-ahf„,

D_nk_x = hfn), D_nk₂=k_b                            (2)

'Работа выполнена при финансовой поддержке РФФИ (проекты 11-01-00106 и 11-01-00224)

О_пкз = М<.Уп + Рз 1^1 + Рз2^к2 ) + «32^2 , ^Dn^k4 = ^к3 ⁺ «42^2 , где И - шаг интегрирования, а,р,, Ру и «у — числовые коэффициенты, ку 1<4, — стадии метода, Е — единичная матрица, f_n=df/dy - матрица Якоби задачи (1). Подставим разложения к, в виде рядов Тейлора в первую формулу (2). Полагая у_п= y(t^ и сравнивая полученное представление с рядом Тейлора для точного решения, запишем условия четвертого порядка точности

• 1)    А + Т>2 + 0 + «32)Л + 0 + «32 + «42М =¹,

• 2)    ару+2ар2+(а + Рзу+Рз2+Заа₃2)рз + +(2а + Рзу + Р32 +4а«з2 + Заад2)Р4 =0-5 , 2        2        2                        2

• 3)    а рууЗа Р2+(а + 2а рз । + Зарз2 + 6а «32)^3 +

+(3а уЗарзу у4арз2 +10а «32 + 6а «42)^4 = 1/6 ,

• 4)    а³ру + ^Р2 + (а³ + За^ Р3 । + 6а² Р32 + +10а^аз2)рз +(4а³ уба^Рзу +10а² Р32 +

  
  

20а3«з2 + 10а3«42) Р4 =1/24,

• ⁵)    (Z%1+/%2)²(РЗ+Р4) = 1^/3,

• 6)    а(Рзу + Р32ХР31 ^РзУХРЗ +^4)=^1/8^

• 7)    а(/%₁₊/%2)²(0.5_№+^4) = 1/24,

• 8)    (/%1+^₂)³(№+^4) = 1/4.

Применяя метод (2) для решения тестовой задачи

У = ^, уф) = у0Л>0,

имеем условие L -устойчивости численной формулы (2) вида

а(а - рг) + (/З31 -а)р3 = 0.

Исследуя совместность этого соотношения и (3), запишем

76а2 - 29а + 3

Р1=-------3----, Р2 =

27а2

146а2 + 89а-12

«32 =

4-16а л

Р4 — ’ Р31 =

27 а

-54а2 + 57а-12

27а2

48а-9 32а

32а-4

РЗ =------ 27а

9-24а

32а ’

8а-32а2

, «42 =

-864а3 + 828а2 -288а+ 36

а(4-16а)2

где а определяется из необходимого условия L -устойчивости

24а4 - 96а3 + 72а2 - 16а +1 = 0 .

Данное уравнение имеет четыре вещественных корня ау =0.10643879214266, а2 =0.22042841025921, а3 =0.57281606248213, а4 =3.10031673511599.

Для расчетов рекомендуется а=0.57281606248213, потому что в этом случае схема (2) дополнительно является Л-устойчивой.

Для контроля точности вычислений метода (2) четвертого порядка будем применять метод третьего порядка вида

Уп+и =Уп + ^1 *Ь2к2 + М<3 + Ь4к5 , где 1),к==кл. a кь 1<3, определены в (2). Нетрудно видеть, что требования третьего порядка имеют вид by + Z>2 + (1 + «32)^3 + О + «32 + «42)^4 -1, aby +2ab2 + (а + рзу + Р32 + 3а«з2)^з + (За + Рзу + Р32 +5а«з2 +4^42)64 = 1/2 , а ЬууЗа b2+(a + 20/^1+30/^2+60 «32)63 +

7                             7            7

+(6а + 4аДз| +5а/?з2 + 15а «32 + 10а «42)64 =1/6, (/%1+/%2)2(*3+*4) = 1/3, где коэффициенты а, /?зь Д32. а32 и а42 заданы в (4). Данная система линейна относительно параметров bh 1<4. При применении коэффициентов (4), имеем by = 1.203100567018353, 62 =-6.552116304144386ЛО"1,

63 = 7.115271884598151-10-1, 64 =-1.189345958672225 Л0"1.

Оценку максимального собственного числа v„0=6|2„max| матрицы Якоби системы (1), необходимую для перехода на явную формулу, оценим через ее норму по формуле

Л/.О =11 5/ / Sy ||= тах^,^ ^у₌₁| dft (у_п WyjV

2.    Контроль точности и устойчивости метода Мерсона

Одним из самых эффективных явных методов типа Рунге-Кутта четвертого порядка точности является метод Мерсона [7]

1, h

Уп+1 - Уп +"7^1 ⁺ Т^4 ⁺7^5 ,

6     36

к\=М<Уп) - к2=кДУп+^кУЬ k3^hf(yn+7kl+7k2^(5)

3                  66

1      3                         1

64 = ШУп + 7^1 + ~^кз) ■ ^к5 = М^п + 7^1 ОО       2

Пятое вычисление функции / не дает увеличение порядка до пятого, но позволяет расширить интервал устойчивости до 3.5 и оценить величину локальной ошибки 6„4 с помощью 6г, то есть

<5^4 = (2^з - 9^з + 864 - 65 ) / 30 .

Для контроля точности будем применять неравенство ||6„4||<5г5 4, которое получено с учетом накопления глобальной ошибки из локальных ошибок [5]. Несмотря на то, что обоснование неравенства проведено на линейном уравнении, оно с достаточно высокой надежностью использовалось для решения нелинейных задач.

Теперь построим неравенство для контроля устойчивости. Применяя к разности 63—62 формулу Тейлора с остаточным членом в форме Лагранжа первого порядка, имеем k3 "к2 = hYQJW /с№2 "Ч'Мб, где вектор рп вычислен в некоторой окрестности решения y(f„). Учитывая, что 62-61=62/Х/3 + О(63), для контроля устойчивости (5) можно использовать неравенство v„ 4 = 6 max | (63 -62)/ / (62 -ку\ |< 3.5, 1<У где числу 3.5 равна длина интервала устойчивости. Отметим, что по мнимой оси область устойчивости также ограничена числом 3.5 (рис. 1). Введем обозначения е„4=6п4/5. Тогда для контроля точности схемы (5) можно применять неравенство спдАг'Д. а для контроля устойчивости следующее - v„4<3.5.

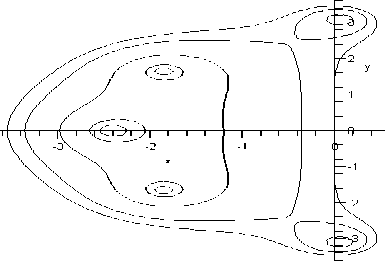
Рис. 1. Область устойчивости метода (5)

Так как оценка максимального собственного числа v„4=/7|2„ _тах| является грубой, то контроль устойчивости используется как ограничитель на размер шага интегрирования. В результате прогнозируемый шаг h,^ вычисляется следующим образом. Новый шаг h^ac по точности определим по формуле h^ac=q\h_n, где h_n есть последний успешный шаг, a ^i, учитывая соотношение e_n^=OQi⁵^, задается уравнением ^⁵ie„₄h^st по устойчивости зададим формулой h^st=qji_m где ^₂, учитывая соотношение v_nA=OQi^, определяется из равенства qiv_nA=3.5. Тогда прогнозируемый шаг /7„₊₁ вычисляется по формуле

И_п+^ = тах[/7_й,тш(/7^яс ,h^st)A •

Данная формула стабилизирует шаг на участке установления решения, где определяющую роль играет устойчивость.

3.    Алгоритм интегрирования

На основе построенных методов легко сформулировать алгоритм переменного шага, в котором на каждом шаге выбирается наиболее эффективная численная схема. Расчеты всегда начинаются явным методом потому, что в нем не используется матрица Якоби. Нарушение неравенства v„₄<3.5 вызывает переход на L -устойчивую схему. Передача управления явным методам происходит в случае выполнения неравенства v„o<3.5, где оценка v„o вычисляется через норму матрицы Якоби. Норма ||^|| в неравенствах для контроля точности вычисляется по формуле

||£||= шах {|§ \К\^_п |+г)},                              (6)

l

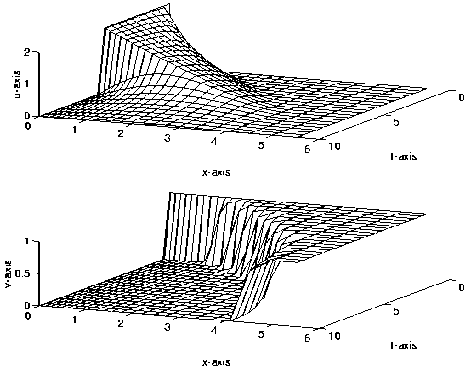
семейство преобразований Мебиуса С х/(х с). с>0. Это замена переменных преобразует ST в прямоугольник {(£ ty 0<^<1, 0 / 7}. Через переменную С задача (7) переписывается в виде дм д7

(^-1)⁴ д²м 2(^-1)³ дм , dv , с¹ д^² с^{1 9}С 5t

с начальными w(£0)=0, v(^,O)=vo, f>0 и граничными м(0, к)=Ф(уу дм(1,7)/д<^=0, 0

и j _ । ^— 2г/ j + г/у₊^

(a^)2

1<7<^.

Значения м0 и uN^ получены из граничных условий, они имеют вид м0=Ф(7), у=(мь vb м2, v2,..., mn, vN)7 и 77=20, эта задача имеет вид г/д^+i—г/д^. Полагая

y'=f(t,y), y(O)=g, y^R2N, 0<7<20, где N- параметр, а функция/определяется формулами

№_У +1 " У2]-3    E2j-3 " 2У2]-1 +   +1

J2 j-I^=a j--------⁺ Pj-----------7-------

2a^ j

-^2 j-V2 j, /2/ = "кУ2 ]У2/-1, где g=(O,vo,O,vo,... ,O,vo)7, a^TXy E^-Xf of fipyj-MfXf с\ M=\JN, 1EJEN, у^)=Ф^У уж+1= Уж-ъ Функция Ф^=2 при О<7<5 и Ф^=0 при 5<7<20, то есть Ф0) имеет разрыв первого рода в точке 7=5. Согласно [8] подходящими значениями для параметров k, v0 и с являются 7 100. v0=l и с=4. Расчеты проводились при 7V=400, то есть система (9) состоит из 800 уравнений. Задача о нахождении разрыва функции Ф(1) при 7=5 возлагалась на алгоритм управления шагом. Решение задачи (9) приведено на рис. 2.

Рис. 2. Решение задачи (7)

Расчеты проводились с двойной точностью. Параметр г в формуле (6) выбирался таким обозом, чтобы фактическая точность вычисления решения совпадала с задаваемой точностью. Сравнение проводилось с приближенным решением, которое получено при задаваемой точности вычислений е=10 ⁹ различными методами. Матрица Якоби вычислялась численно. В табл. 1 приведены результаты расчетов при различных значениях задаваемой точности вычислений е. Вычислительные затраты приведены в форме ifljfy где через if и ij обозначены соответственно число вычислений правой части и декомпозиций матрицы Якоби на интервале интегрирования. В табл. 1 используются обозначения: RK4 - метод Мерсона, RK4st - метод Мерсона с контролем устойчивости, МК4 - L-устойчивый метод, RKMK4 - алгоритм с автоматическим выбором численной схемы.

Таблица 1

Результаты расчетов

Метод / e	RK4	RK4st	MK4	RKMK4
10 2	1 017 921	883 561	39 560(49)	35 286(34)
10 3	1 018 024	886 914	62 918(78)	44 923(46)
10 4	1 018 177	889 604	76 717(95)	66 845(74)
10'	1 018 701	882 836	92 165(114)	83 984(86)
10 ”	1 019 268	916 280	103 687(128)	96 205(99)

Из сравнения результатов расчетов RK4 и RK4st следует, что на данной задаче контроль устойчивости приводит к сокращению вычислительных затрат более чем на 10%. Это является следствием устранений некоторых повторных вычислений решения, возникающих за счет неустойчивости численной схемы. На других задачах преимущество RK4st перед RK4 может достигать 50% [5]. Из сравнения результатов расчетов МК4 и RKMK4 следует сокращение числа декомпозиций матрицы Якоби, что является следствием расчета некоторых переходных участков по явной численной формуле.

Заключение

В RKMK4 с помощью признака можно задавать различные режимы расчета: 1) явным методом с контролем или без контроля устойчивости; 2) L-устойчивым методом с аналитической или численной матрицей Якоби; 3) с автоматическим выбором численной схемы. Все это позволяет применять данный алгоритм для решения как жестких, так и нежестких задач. При расчетах с автоматическим выбором численной схемы вопрос о том, является ли задача жесткой или нет, перекладывается на алгоритм интегрирования.