Алгоритм корреляции структурно резервированной информационно-телекоммуникационной сети с учетом применения противником средств и методов противодействия

Информационный поток связывает источники с потребителями информации и определяется элементами и схемой. Схема потока определяет взаимосвязь потоковых элементов в процессе их образования. Для построения схемы потока необходимо знать, на основе каких элементов формируется каждый потоковый элемент.

В распределенной системе, к которой относится информационно-телекоммуникационная сеть (далее – ИТКС), защитить информацию гораздо сложнее, чем в централизованной. Поэтому важным свойством ИТКС, которое необходимо учитывать при решении задачи синтеза, является обеспечение безопасности информации, циркулирующей между управляющими системами (далее – УС) ИТКС [1].

С учетом этого необходимо синтезировать ИТКС на основе предполагаемых воздействий противника, обосновать структурно резервированную ИТКС и рациональное количество резервных каналов связи [4].

Лукин Константин Игоревич

С этой целью предлагается алгоритм корреляции структурно резервированной ИТКС с учетом применения противником средств и методов противодействия [5].

Структурная схема алгоритма, реализующего данную процедуру определения рационального варианта расчета, приведена на Рисунке 1.

S,

Таким образом, можно определить зависимость min^ t^ (х) = f (Cйоп), каждой точке k=1

которой соответствуют свои оптимальные с точки зрения функционала значения параметров структуры ИТКС.

При увеличении уровня отпускаемых на ИТКС средств ( С _доп) реальная ее стоимость S

C*S = 2 ^a k m k (S) C 1 увеличивается, асимптотически приближаясь к предельному значе- k = 1

Алгоритм корреляции структурно резервированной информационно-...

нию, уровень которого соответствует стоимости ИТКС с параметрами решения задач на каждом уровне, близкими к значениям НЮЮЮ_k ( S ) [12].

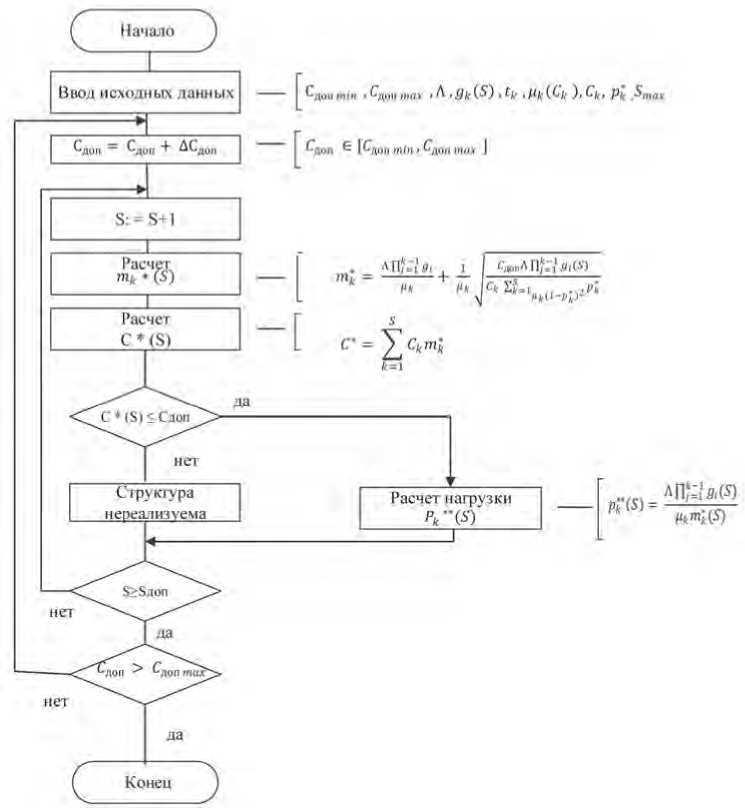
Рисунок 1. Алгоритм определения рациональных вариантов структуры ИТКС по минимуму времени обработки информации на УС

S

Выполнение неравенства С ^* =^ a k m k (S) C 1 <  C _8on свидетельствует о том, что такая структура не может быть реализована в данной системе исходных данных, а при S

Cs =£ a k m k (S) C 1 <  С mn ее реализация не отвечает системе основных ограничений [6; 7]. Из результатов расчетов можно заключить, что множество M ( S, m k , Л ) допустимых с точки зрения соответствия системе ограничений структур при увеличении интенсивности информационных потоков сужается, то есть справедливо отношение

M ( S , m _k, Л 2 ) c M ( S , m k , Л 1 ) при Л 1 <  Л 2 .

Идеальной структурой в множестве допустимых M ( S, m k , Л ) была бы структура, обеспечивающая минимум времени обработки информационных потоков и имеющая минимальную стоимость. Эти требования, как уже указывалось выше, противоречивы [9; 11; 15]. Их разрешение осуществляется методами векторной оптимизации, в рамках которой необходимо определить не только структуру с максимальной оперативностью обработки информационных потоков, но и структуру с минимальной стоимостью [14].

Для обеспечения глобальной оптимизации структуры необходимо рассмотреть обратную задачу, суть которой заключается в определении таких параметров структуры ИТКС, при которых стоимость ее организации и технического обеспечения будет минимальна, а основные и вспомогательные критериальные функции будут отвечать требуемой системе ограничений, то есть при условии

min S ₁ m ₁, m ₂,

S ms-1 Z Ckmk к=1

S

Z t ki + t kk ^ t _aon ,                                       (2)

к = 1

где t _доп – допустимое время передачи пакета сообщения в структуре ИТКС, определяемое исходя из технических, организационных и тактических соображений. В формуле (2) параметр t _ki определяется как сложная функция, зависящая от внутренней структуры S ( m k )) и параметров УС ( ц _к t kk ), а также от величины поступающего на вход ИТКС информационного потока.

Тогда dL (mk, Ck)

a m

= C k - в

к - 1

Л П g.

1 -----^ы-------> = 0.

k - 1

m -лП g.

V

. = 1      7

Преобразуя (3), получим выражение для неопределенного множителя Лагранжа [17] k

Z t k C k (1 - Р *)

в =

k = 1

-*" доп

S - 1

- Z t kk

k = 1

Так как по условию выполнения ограничений на вспомогательные критерии р * = const, то

k

(1 - Р *)Za в «---—

S - 1        ,

k

доп -Ztkk k=1

После несложных преобразований получим:

Алгоритм корреляции структурно резервированной информационно-...

где

k - 1

A k. ^Л П g j

**         \ j = 1

m k =----------

P k

k = —1— m_kA_k

• ¹        k - 1

-+ЛП gj;

j = 1

' k - 1

ЛПgj, j=1

A k =

Г            k

V

S - 1

T on - I t kk

V

.

Принимая во внимание ограничение (1), окончательно из (5) получим

(

S

E C k m k =

TSon -

J k - 1

C k ^Л П g .

^j = 1

Z1 ^k ^ ^{(1 - p} k )

'

.

Решение задачи для конкретного значения S обеспечивается полученными выше уравнениями (6) и (7). Аналогично, как и в рассмотренном выше алгоритме, синтезируемые параметры структуры ИТКС определяются последовательно для различных уровней ( S = 2, … ‚ S _доп) иерархии внутренней структуры УС [10]. Для каждого значения параметра S = 2, S _Son определяется оптимальное число УС по уровням иерархии ( m _k ** ), при кото

** ром обеспечивается, с одной стороны, минимум стоимости структуры, то есть / .C k m k , а с другой – удовлетворяются ограничения по времени передачи пакетов сообщений. Глобальный оптимум параметров структуры соответствует такому значению уровня иерархии S ^**, при котором обеспечивается минимум стоимостных затрат на реализацию и поддержание устойчивости функционирования ИТКС, то есть

{ **    **

S , m k } => min

S

Е ** m_kC_k . , m ..., m

• i ,    2 , ^s - 1 k = 1

Структурная схема алгоритма расчета рациональных (с точки зрения стоимостных затрат) параметров структуры ИТКС с учетом ограничений на допустимое время передачи пакетов сообщений приведена на Рисунке 2.

Найденные значения оптимальных распределений УС по уровням иерархии структу-

{ *    *                 *

и стоимостных

S , m k ( ■ ) : k = 1, S -

{S ,mk (■): k = 1,S -1} критериев образуют локальные идеальные векторы распределений. Последовательно присваивая S = 1, 2, 3, … , фиксируем S*(m*k) или S**(m**k), обеспечивающие минимум критериальных функции организации структуры по времени и по стоимости.

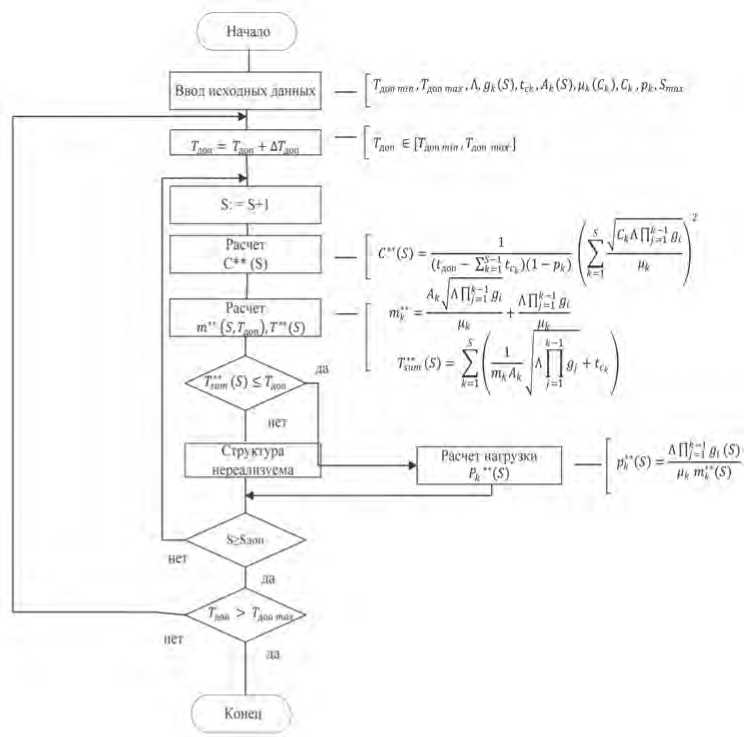
Рисунок 2. Алгоритм определения рациональных вариантов структуры ИТКС по минимуму стоимости

Можно показать, что S * <  S ** .

*    *                 *                **    **                 **

S ,mk (■): к = 1,S -1} и {S ,mk (■):к = 1,S -1} рассматриваются как глобальные идеальные векторы и определяют границы области компромиссов многокритериальной задачи векторной оптимизации структуры ИТКС [13].

Формулирование базового варианта задачи УС ИТКС

Задача уточнения базового варианта численности и квалификационной структуры УС ИТКС может быть сформулирована следующим образом. Необходимо из заданной обла- сти допустимых изменений вектора А с Ao найти такой вектор А * рациональных значений характеристик численной и квалификационной структур ИТКС, при котором векторный показатель качества линий связи (Е), включающий в себя приведенные стоимостные затраты (С) на эксплуатацию ИТКС и эффективность работы (P(А)) в условиях воздействия противника, будет оптимален при условии, что совокупность определенного множества характеристик ю (А) сети будет удовлетворять заданной системе ограничений (too):

Алгоритм корреляции структурно резервированной информационно-...

E = < C ( A ) ; P ( A ) >  ^ opt ,

A A' Ao.

Система ограничений to ° в уравнении (9) определяется множеством допустимых векторов ( А ^o) численных и квалификационных структур отдельных УС; множеством допустимых вариантов организации связи і -й и j -й УС ( A_i^o_j ); множеством информационных потоков от j -го УС к і -му УС; совокупностью ограничений на время передачи пакетов сообщений через каждый УС и для расчета в целом.

Вероятность своевременной и безошибочной передачи информационных потоков может быть определена произведением

р( Л, ) = P. (Л,) F (As ti).

где P_{i CT} ( A , ) - вероятность безошибочной передачи i -го информационного потока при условии, что вектор численной и квалификационной структуры -х УС равен A ; F ( A i ; t i <  t ° ) - вероятность своевременной передачи информационных потоков i -м УС.

Для определения временных характеристик обработки (передачи) пакетов сообщений введем следующие допущения: информационный поток для всех УСі представляется как простейший поток, время обработки пакетов сообщений УС распределено по экспоненциальному закону [3].

Время обслуживания информационных потоков различными УС рассматривается как смешанное время произвольного вида [16].

Учитывая данные допущения, время обработки информации отдельными УС определим как

v A pk iCMk1)

k ^{( A} k x k ) = v-l

1 - A pk i sMk(-1

+

(2) k k iCMk 2)

7 v

2 1 — A P ik

х ^+v k ,

(    ^- Mi3)

1 - A p k

-m;’   J

где k e ^M ; p ,k = ,k,k ;

M k ^{( 1 )} - подмножество пакетов сообщений, имеющих более высокий абсолютный приоритет, чем информационный поток k ;

• ( 2 )

M_k – подмножество информационных потоков, по отношению к которым пакеты сообщений k не обладают более высоким приоритетом;

M_k ^{( 3 )} - подмножество информационных потоков, имеющих более высокий относительный или абсолютный приоритет по отношению к пакетам сообщений k ;

M k ^{( 4 )} - подмножество пакетов сообщений, по отношению к которым информационный поток k не обладает более высоким относительным или абсолютным приоритетом;

X _k v k - среднее время обработки (передачи) пакетов сообщений k -го и i- го информационных потоков, обрабатываемых k -й подгруппой УС;

A ik - интенсивности поступления на обработку пакетов сообщений i -го информационного потока, обрабатываемых k -й подгруппой УС;

v i ^{( 2 )} - коэффициенты вариации i -го информационного потока.

Время передачи информационных потоков УС ИТКС может быть определено по формуле t (Aix, ; AjjXY ) ^ aij tjj (Ax ; Ax ) ’

• i ,    j £ M°

где t ij - время передачи j- х пакетов сообщений ( i е М°) УС i -й иерархии;

Aij а =—”- коэффициент передач, определяющий процентное количество обращений A к i-му УС.

Итак, будем считать, что в результате решения задач вида (9) последовательно в отно шении двух функционалов t(■ ) и С( ■ ) найдены их оптимальные значения [2]:

. °       .

t min =

S ( m_k )

{ t * ( ^S ( m k ) , C don ) ;

C = min { C * ( S ( m k ) , C ₈o„ ) ;

S ( m k )

t ** ( ^S ( m k ) , t 8on ) }

C ** ( ^S ( m k ) , t do« ) ^} ;

( Sm_k ) с M ( S , m k , Л ).

Очевидно, что из анализа условий существования решений прямой и обратной задач, определяемых приведенными выше утверждениями, справедливо соотношение

*      *    **      **

S (ms ) S (ms ),

где

S ( m s ) = ( m i* , m 2* , ^ , m s * - 1 ,1) ;

**      **          **     **         **

S ( m s • ) = ( m i , m 2 ,..., m s -- 1 ,1) .

Тогда условие нормировки критериев будет иметь вид t0

t^( S ( mk ))= t ( S ( m )) ’1 ( S ( mk ^ 6 { t ( S ( mk )), t ( S ( mk ))} ;

^{C ( S (} m k ^{)) =} C (^ m ) ) ’C ^{( S (} m k ) ) ⁶ { C * ^{( S (} m k ) ) , C" ^{( S (} m k ) ) } ’ где S ( m_k ) – структуры из области допустимых структур УС ИТКС, то есть

S ( m_k ) с M ( S, m k , Л ).

Окончательное решение задачи оптимизации структуры системы управления формально может быть представлено следующим образом:

max      { ^a i t _H ( ^S ( m k ) ) + « 2 C _H ( ^S ( m k ) ) } ,

S ( m k ) c M ( S , m k , Л )

где а1, a2 - соответствующие данному классу задач коэффициенты равнозначности нор мированных векторных критериев tH (■) и CH (■).

Алгоритм корреляции структурно резервированной информационно-...

Рассмотренный алгоритм позволяет рассчитать основные параметры ИТКС исходя из структуры УС. Эти параметры следует рассматривать как опорный вариант ИТКС, служащий основой для принятия решения экспертом о целесообразности или нецелесообразности дальнейшего изменения структуры ИТКС [18].

При этом выбор метода оптимизации структуры ИТКС осуществляется на основе анализа характера исходных данных и глубины детализации структуры ИТКС с учетом стоимостных и прочих ограничений [19].

Описанные выше аналитические методы определения рациональных параметров ИТКС эффективно могут быть использованы в условиях значительной неопределенности исходных данных о характере и внешних условиях функционирования УС. Аналитико-статистические методы в рамках решения этих задач служат средством уточнения параметров структуры на основе более полного учета факторов, определяющих особенности передачи информационных потоков между УС.

Таким образом, подсистемы, обслуживающие аналитико-статистические методы априорной оценки параметров ИТКС, можно рассматривать как инструментальные средства поддержки принятия решений в процедурах обоснования потребной численности УС [8].