Алгоритм на основе сэмплирования аэрозольных неоднородностей в задаче измерения скорости ветра

На данный момент существует ряд важных практических приложений дистанционного и оперативного мониторинга скорости атмосферного ветра: метеорологическое обеспечение взлёта и посадки летательных аппаратов, мониторинг ветровой обстановки, контроль аэрозольных загрязнений, научные исследования аэрозольных полей и увеличение эффективности работы ветрогенераторов. Каждая из них предъявляет высокие требования к точности и быстродействию измерений. Необходимым требованиям удовлетворяют оптические методы измерения, в частности лидарные. Большинство лидарных методов измерения скорости и направления ветра основаны на зондировании атмосферного аэрозоля, который полностью увлекается воздушными потоками [1–9].

Лидарные методы для задач измерения скорости ветра можно условно поделить на две группы: доплеровские и времяпролётные [4]. Наиболее распространённым является доплеровский метод, позволяющий определять с высокой точностью скорость и направление ветра. Его недостатками являются большое время обновления данных и необходимость пространственного осреднения с использованием конического сканирования атмосферы по азимуту с большим углом места, а значит, и невозможность работы в условиях сложного рельефа местности [7].

Времяпролётные методы измерений включают ряд следующих: корреляционный, структурный и трассерная визуалиция потоков. Их преимуществами по сравнению с доплеровскими являются большое быстродействие за счет отсутствия необходимости пространственного сканирования атмосферы и меньшая себестоимость приборов. Однако по сравнению с до- плеровскими методами они обладают худшей точностью измерений скорости ветра, поэтому перспективно развитие времяпролётных методов с целью увеличения точности измерений.

Одним из направлений улучшения качества время-пролётных методов является улучшение методов обработки лидарных сигналов и изображений. Лидарный сигнал существенно зависит от состояния атмосферы и является нестационарным по дальности зондирования и времени измерения. Получение полезной информации из такого сигнала для определения скорости и направления ветра с приемлемой точностью будет сильно зависеть от качества методов цифровой обработки. Для решения задачи выделения полезного сигнала в таких случаях подходят алгоритмы с адаптивной фильтрацией, вейвлет-обработка и др. Отметим, что наиболее перспективным методом обработки является использование нейронных сетей, которые при наличии достаточного количества данных показывают наилучшие результаты по сравнению с классическими методами цифровой обработки [10–14].

Статья посвящена разработке алгоритма обработки изображений в координатах «дальность – время» для задачи измерения скорости и направления ветра на основе времяпролётного метода и апробации разработанного алгоритма на синтезированных и экспериментально полученных аэрозольных полях.

Математическая модель лидарного сигнала и перемещения аэрозольных неоднородностей под действием ветра

Времяпролётные методы измерения основаны на регистрации перемещения аэрозольных частиц и аэрозольных неоднородностей атмосферы – допускается, что аэрозольные частицы полностью увлекают- ся ветром и их скорость совпадает со скоростью ветра. В приземном слое атмосферы время жизни аэрозольных неоднородностей составляет от единиц до десятков секунд, а их размеры – от одного метра до десяти метров и более, причем с увеличением высоты над земной поверхностью размер неоднородностей увеличивается. При дальнейшем рассмотрении неоднородностей принимаются следующие типовые допущения: неоднородности изотропны и время их жизни больше времени измерения. При лазерном зондировании для измерения скорости и направления ветра используют коэффициент обратного аэрозольного рассеяния, в вариациях величины которого проявляются неоднородности [9].

При наличии ветра неоднородность перемещается в пространстве, и её перенос r _i за время измерения Δ t можно оценить через среднюю за время измерения скорость ветра V :

r _i = V Δ t .

Для моностатической схемы измерения среднюю за время измерения скорость ветра можно представить в виде (рис. 1):

• V = V cos a ,

• V _⊥ = V sin α ,

где α – угол между направлением зондирования (оптическо й осью лидара) и направлением атмосферного ветра, V , V _L - продольная и поперечная (относительно направления зондирования) компоненты скорости ветра.

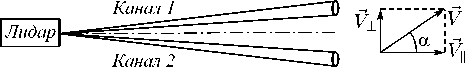
Рис. 1. Схема измерения скорости ветра

Аналогично можно представить перенос аэрозольной неоднородности:

• r = r cos a ,

• r _⊥ = r sin α .

где r , r - перенос неоднородности в продольном и поперечном (относительно направления зондирования) направлении.

Регистрируемый лидарный сигнал в общем случае имеет вид [4]:

U ( z ) = K ( P ( z )) ■ P ( z ) = K ■ P ( z ),

P(z)=1 A(z)β(z)T(z), z2

где z – расстояние от лидара до зондируемого объема атмосферы, K – передаточная функция электронного тракта, P ( z ) – мощность обратно рассеянного сигнала, A ( z ) – аппаратная функция лидара, T ( z ) – коэффициент пропускания атмосферы, β ( z ) – коэффициент обратного рассеяния атмосферы.

Аэрозольные неоднородности проявляются в виде флуктуаций коэффициента обратного аэрозольного рассеяния. В соответствии с этим можно записать:

β(z) = β(z) + β(z), где β(z), β(z) – средняя по ансамблю реализаций и флуктуационная компоненты соответственно.

Регистрируемый лидарный сигнал без предварительной калибровки не позволяет найти абсолютную величину β ( z ), но позволяет определить относительные флуктуации коэффициента обратного рассеяния:

_дв = в = P i ( z ) - P ( z ) ₌ U i ( z ) - U ( z )

i β P(z) U(z) , где Pi (z),Ui (z) – регистрируемая мощность и сигнал реализации в момент времени ti, P(z), U(z) – усреднённый по ансамблю реализаций профиль мощности и регистрируемого сигнала.

Каждая из регистрируемых реализаций в момент времени t i , i= 1 … N позволяет получить относительный коэффициент обратного аэрозольного рассеяния Δ^β _i ( z ), а последовательность таких реализаций за время измерения Δ t формирует поле относительных флуктуаций аэрозольных неоднородностей Δ _i ^β _j , j = 1 … M , где M – размер регистрируемой реализации. Полученное поле Δ ^β в координатах «дальность – время» содержит информацию о переносе неоднородностей и позволяет измерить продольную и поперечную компоненту скорости ветра. При обработке поля Δ ^β можно рассматривать как изображение с целью применения методов цифровой фильтрации, основанных на локальных характеристиках. Обработка сигналов и анализ неоднородностей производится при допущении, что в локальной области характеристики сигнала можно считать стационарными по дальности и времени. Основные этапы измерения скорости ветра представлены на рис. 2.

Этап формирования поля флуктуаций Δ ^β тестировался предварительно на синтезированных данных, а затем с использованием данных натурных измерений. Синтезированные данные формировались с использованием метода формирующего фильтра [15].

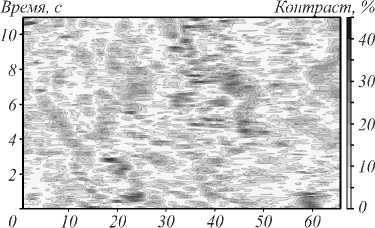
При моделировании использовались 20 вариантов пространственных полей флуктуаций с известной корреляционной характеристикой размером 300×300 м. Для моделирования были использованы скорости ветра от 0 до 15 м / с с шагом 0,1 м / с с различными направлениями относительно лазерного луча. Ширина корреляционной функции составляла величины от 0,5 до 10 м с шагом 0,5 м. При моделировании эхо-сигнала добавлялась флуктуация мощности лазерного импульса с СКО 1 % и белый шум, моделирующий нестационарность сигнала по дальности. Пример смоделированного поля в координатах «дальность – время» представлен на рис. 3, где «дальность» – дальность от лидара до объема атмосферы, а «время» – время измерения.

Время измерения

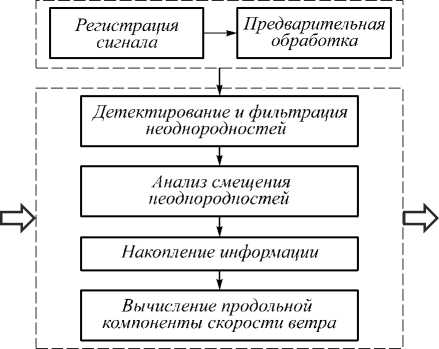
Рис. 2. Основные этапы вычисления продольной компоненты скорости ветра

Дальность, м

Рис. 3. Пример синтезированного поля аэрозольных неоднородностей: V ^⊥ = 2,0 м / c, V ^|| = –3,0 м / с

Натурные данные измерений получены с использованием лидара [16]. Пример поля неоднородностей Δ ^β в координатах «дальность – время», полученного из натурных данных, представлен на рис. 4.

Диапазон дальности, .м

Рис. 4. Пример поля аэрозольных неоднородностей: V ^⊥ = 2,3 м / c, V ^|| = 1,0 м / с

Цель блока детектирования и фильтрации неоднородностей – выделение на изображении наиболее контрастных неоднородностей. В качестве алгоритма выделения неоднородностей использовался алгоритм сегментации [16]. Пример выделения наиболее контрастных неоднородностей представлен на рис. 5.

Алгоритм измерения скорости ветра

Задача измерения скорости ветра с использованием предложенной схемы измерения состоит из двух подзадач – измерения продольной и поперечной относительно направления зондирования компонент скорости ветра.

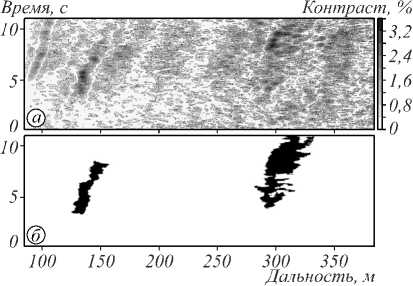
Рис. 5. Результат применения алгоритма сегментации аэрозольных неоднородностей: поле после предварительной обработки (а); поле после блока детектирования и фильтрации неоднородностей (б)

Наиболее простой схемой измерения одновременно и продольной, и поперечной скорости ветра является двухлучевая схема (рис. 1). Измерение скорости ветра происходит на основе анализа взаимного смещения неоднородностей в канале 1 и канале 2 (в блоке анализа смещения неоднородностей на рис. 2).

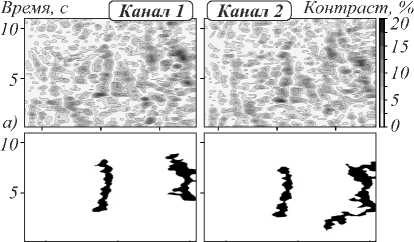
Исходными данными для работы блока анализа смещения неоднородностей являются поля флуктуаций Δ ^b в координатах «дальность – время», зарегистрированные в канале 1 и 2 (рис. 6).

150    200

Дальность, м

100    150    200 100

б) Дальность, м

Рис. 6. Результат применения алгоритма сегментации аэрозольных неоднородностей для двух каналов: поле после предварительной обработки (а); поле после блока детектирования и фильтрации неоднородностей (б)

Рассмотрим процесс перемещения аэрозольных неоднородностей в продольном направлении. В течение времени измерения неоднородность переносится через лидарный луч под действием ветра, и регистрируемый лидарный сигнал Pi (z) содержит профиль перемещающихся неоднородностей. При регистрации сигнала можно считать, что центру неоднородности соответствует максимальное значение флуктуации в реализации Δiβ , то есть пик в локальном срезе сигнала. Таким образом, регистрация последовательности пиков Δiβ фиксирует положение каждой из неоднородностей в момент времени ti, а значит, содержит информацию о перемещении в продольном направлении. Существует ряд подходов к детектированию пиков в сигнале, таких как использование корреляционного анализа, цифровой фильтрации, пороговой обработки сигнала и распознавание образов [13, 17]. В предложенном алгоритме используется алгоритм детектирования пиков на основе вейвлет-преобразования сигналов [18].

Представим осреднённую за время и диапазон дальности измерения продольную компоненту скорости ветра как среднюю скорость перемещения аэрозольных неоднородностей:

V    = 12 V,

KK где K - общее число неоднородностей, Vk - продольная скорость перемещения неоднородности:

• V I    = ^

k    A t ’ где Ark - перенос неоднородности между начальным и конечным моментом измерения.

Множество факторов, влияющих на точность измерений: турбулентность, шумы электронного тракта, джиттер лазерного импульса – ухудшают качество проводимых измерений. Чтобы использовать накопленную информацию о перемещении и получить осреднённый устойчивый результат, воспользуемся функционалом для средней ошибки перемещения неоднородностей:

F (V " ) = -¹ 2 f V " ),                         (1)

KK где fk(V||) - функция ошибки определения скорости ветра для неоднородности k, K – количество неоднородностей. Минимизация функционала F(V ||) позволяет определить продольную компоненту скорости:

• V ¹¹    = arg min F(V ¹¹),

• V II е В

где V ¹¹ - полученное значение скорости ветра.

При нахождении значения продольной компоненты скорости ветра вид функции ошибки для каждой из неоднородностей может учитывать структуру самой неоднородности и включать более детальную информацию о накопленных данных. В простейшей версии алгоритма реализована неравномерность отношения сигнал/шум для пика неоднородности во время измерения. Запишем для каждой неоднородности функцию ошибки с учётом сэмплирования пиковых значений коэффициента флуктуаций (рис. 7):

f k (V " ) = 2 w k (V " t s — r s ) 2 ,

s где s – номер сэмпла для неоднородности, wsk – вес для каждого сэмпла, rs – положение координаты неоднородности в момент времени ts. Веса для каждой компоненты в функции ошибки прямо пропорциональны от максимальной амплитуды флуктуаций в сэмпле и нормировались на L2-норму:

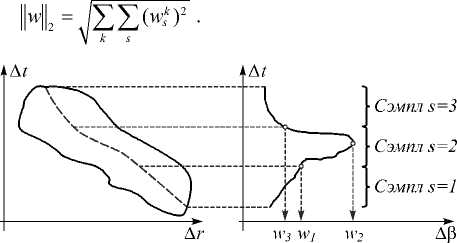
Рис. 7. Сэмплирование неоднородности для формирования функционала

В отличие от продольной компоненты, измерение поперечной компоненты скорости ветра является более сложной задачей. Классическим решением является сканирование в секторе пространства [11]. Однако без сканирования также возможно измерение поперечной относительно луча скорости ветра: использование двух и более лучевых схем, переключение одного луча в малом угле [5].

Рассмотрим двухлучевую схему измерения, когда лучи находятся под малым углом у друг к другу. Поле неоднородностей, полученное для одного луча, позволяет оценить поперечную компоненту по абсолютному значению без учета направления относительно луча [19]. Большая точность может быть получена посредством анализа полей неоднородностей в двух лучах. При этом возможны 2 сценария детектирования неоднородности во время измерения: неоднородность зарегистрирована в одном луче, но не зарегистрирована в другом, и неоднородность зарегистрирована в обоих лучах.

При наличии неоднородности в обоих лучах необходимо установить соответствие для всей области проявления неоднородности. В режиме реального времени при обнаружении неоднородности в одном из лучей сопоставление её более надёжно в случае прогнозирования движения и ожидаемого положения в другом луче, при этом качество детектирования будет зависеть от величины продольной и поперечной компоненты скорости ветра (рис. 8). Для прогнозирования могут быть использованы, например, регрессионные модели или алгоритмы экстраполяции [13, 17].

Допуская, что расстояние между лучами в локальной области одинаковое, в первом сценарии для Vk¹ можно наложить условие:

V^< b^, k A t где b(z) – расстояние между лучами на дальности z, где была зарегистрирована неоднородность. Для определения поперечной скорости ветра воспользуемся функционалом, аналогичным (1):

F(V⊥) = 1 ∑fk(V⊥), KK fk(V⊥)=∑ws(x2 -(b(z)+V⊥τs)), s где s – номер сэмпла при разбиении, ws – весовой коэффициент, x2 – положение неоднородности во 2-м луче, тs - разница по времени для одной области неоднородности в разных лучах.

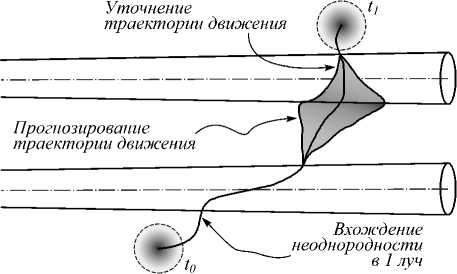
Рис. 8. Определение поперечной компоненты скорости ветра

Для ускорения сходимости функционала можно воспользоваться оценкой компонент скорости ветра на основе размеров связанной области:

уи =ly ^ii start = ∑ k ,

Kk v1 =—У к1

start ⁼ ∑ k ,

Kk где Vk, Vk1 - оценка продольной и поперечной скорости ветра с помощью алгоритма [19] для неоднородности k, знак поперечной скорости определялся номером канала, в котором проявлялась неоднородность.

Объединим измерение продольной и поперечной компоненты. Для заданного времени измерения Δ t , количества зарегистрированных реализаций сигнала N и заданной дальности зондирования, определяемого количеством отсчетов сигнала M , получены срезы поля неоднородностей в каждом из каналов Δ ^β1 и Δ ^β2, дополнительно к ним применен алгоритм сегментации неоднородностей:

• 1)    для Δ^β _i ¹ и Δ^β _i ² вычислить положение и значение амплитуды пиков для каждой неоднородности;

• 2)    установить соответствие неоднородностей между полями для разных каналов;

• 3)    сформировать компоненты ошибки для продольной компоненты;

• 4)    сформировать компоненты ошибки для измерения поперечной компоненты, если неоднородность принадлежит множеству { K ^⊥ } неоднородностей, зарегистрированных в 2 лучах;

• 5)    вычислить стартовое значение параметров;

• 6)    оптимизировать функционал.

В соответствии с этим можно записать:

for i=1…N:

for k=1…K:

[pos,amplitude]_i,k ← find peaks(Δ^β_i) f_k(V " ) <  build_parallel_error M ^{/ ?}, s,k) F (V , v ) < F(V " ,V ^X ) + f_k(V " )

V _start ← ( V _start + V _k )/2

if k ∈ { K ^⊥ }:

f_k(V ^⊥ ) ← build_trans_error( Δ ^β ,s,k) F(V,V ^⊥ ) ← F(V,V ^⊥ ) + f k (V ^⊥ )

V_s™ < ( Vs™ + ^> 1 )/2

V¹ ,V ¹ < argmin F(V^II,V ¹ )

Для анализа работы предложенного алгоритма проведено математическое моделирование с использованием синтезированных полей в координатах «дальность – время» и получены результаты обработки данных натурных измерений. Для сравнения выбраны классический корреляционный алгоритм измерения [9], корреляционный метод с сегментацией неоднородностей [15] и разработанный алгоритм на основе сэмплирования. При сравнении оценивалась средняя абсолютная погрешность (по отношению к показаниям анеморумбометра) для определения продольной компоненты Δ V ^||, поперечной компоненты Δ V ^⊥ . Результаты сравнения представлены в табл. 1.

Табл. 1. Сравнение результатов измерения

	Корр. алг.	Сегментация + корр. алг.	Сегментация + алгоритм сэмпл.
Синтезированные данные
Δ V || , м/c	0,23	0,19	0,10
Δ V ⊥ , м/c	0,37	0,33	0,26
Натурные данные
Δ V || , м/c	0,38	0,30	0,15
Δ V ⊥ , м/c	0,60	0,47	0,33

Заключение

Разработан алгоритм на основе сэмплирования аэрозольных неоднородностей для обработки изображений в задаче измерения скорости ветра для лидар-ного зондирования атмосферы. Разработанный алгоритм протестирован на синтетических данных, полученных с различными корреляционными характеристиками, и натурных данных измерений. Показано, что алгоритм обработки аэрозольных полей в координатах «дальность – время» позволяет существенно уменьшить погрешности лидарного времяпролётного метода измерения скорости ветра по сравнению с корреляционными методами измерения.