Алгоритм настройки системы нечёткого логического вывода типа Мамдани

Использование систем нечёткого логического вывода приобрело широкое распространение, начиная с 1980-х гг., когда разработанные в 1965 году Л. Заде математические принципы стало возможным применить в алгоритмах, выполняемых с использованием ЭВМ. Математическое подтверждение возможности использования нечётких моделей в задачах моделирования функциональных зависимостей получено после доказательства Б. Коско теоремы [1] о том, что системы нечёткого логического вывода типа Мамдани могут аппроксимировать любую функциональную зависимость с заданной точностью (впоследствии аналогичные теоремы доказаны в отношении систем нечёткого вывода типа Сугено). Для настройки правил нечётких моделей существуют различные алгоритмы, наиболее распространенными из которых являются алгоритмы, построенные на основе нейронных сетей или алгоритмы нечёткой кластеризации. Но указанные методы более часто применяются для настройки систем типа Сугено [2–5], в связи с большей вычислительной простотой и точностью. Тем не менее остаётся класс систем типа Мамдани [6–9], которые применяются при реализации экспертных систем, в связи с интуитивной понятностью интерпретации правил и большей близостью к логическому мышлению человека, для которых после настройки системы экспертами требуется корректировка правил нечёткого логического вывода на основе статистических данных, получаемых в процессе функционирования системы.

В качестве объекта применения адаптивного алгоритма возьмем классическую систему нечёткого логического вывода типа Мамдани, содержащую m входных переменных и одну выходную переменную. Каждая входная переменная может содержать от 2 до m функций принадлеж-

Математика

ности к нечёткому множеству. Выходная переменная содержит k ≥ 2 функций принадлежности. Общая схема вывода для систем типа Мамдани производится по следующему алгоритму:

• 1.    Этап фаззификации: чёткие значения входных переменных x приводятся к нечётким значениям посредством вычисления их степени истинности выражения: x u есть A u^j как вычисления значения соответствующего значения входной функции принадлежности µ_A ( x_u ), где u – номер входной переменной, j – номер правила нечёткого логического вывода.

• 2.    Этап нечёткого вывода: используя полученные на первом этапе значения степеней истинности, вычисляются результирующие значения для каждого j -го правила из набора в m правил:

• 3.    Этап дефаззификации: получение чёткого значения. В статье будет рассматриваться модель с выполнением дефаззификации методом вычисления центра тяжести

R_j : ЕСЛИ ( x ₁ естьА ₁ ^j ),...,И( x_n есть А_n ^j ) ТО y есть B_k ^j ,                  (1)

где И – операция пересечения нечётких множеств ( t -норма). В статье в качестве оператора t -нормы используется оператор умножения (оператор MIN), k – номер функции принадлежности выходной переменной.

maxmax y = J УЦг (y) dy   J Цг (y)dy , minmin где µr(y) – результирующая функция принадлежности, полученная посредством суммирования частных усечённых функций принадлежности µjr(y), полученных при срабатывании j-го правила.

Синтез алгоритма настройки системы нечёткого логического вывода

Для применения принципов регулятора, работающего по пропорционально-интегральному принципу (ПИ-регулятор) [10], для каждого правила введём понятие накапливаемой (интегральной) ошибки, рассчитываемой по формуле (3), и пропорциональной ошибки:

N

I ij = Z w j ⁽ y i - s i ),                                        ⁽³⁾

• i = 1

P ij = w j ⁽ y i - s i ),                                             ⁽⁴⁾

где j – номер сработавшего правила; i – номер шага, на котором было получено прогнозируемое значение на выходе системы нечёткого логического вывода y ; S i – реальное значение прогнозируемой величины; w_j – вес вклада результирующей функции принадлежности j -го правила при формировании i -й оценки, вычисляется по формуле:

W j = T ( Ц А1 j ( ^ 1 ), Ц а 2 j ( x 2 ),..., ^ Anj ( X 1 )),                                (5)

где T – операция вычисления t -нормы. В качестве t- нормы нами использована операция MIN, но можно использовать другие варианты t- норм, такие как оператор произведения или оператор усиленного произведения [11]. В представленной интерпретации w i соответствует уровню активации j -го правила при получении результирующей функции принадлежности. Для каждого правила выделим чёткое значение заключения y j , получаемое по тому же правилу, что и общее результирующее значение (6), только в функция принадлежности µ jr ( y ) является результирующей функцией от срабатывания j -го правила:

maxmax yj = J УЦjг(y)dy   J Цjг(y)dy.

minmin

В качестве формы функции принадлежности для описания входных и выходной переменных выбрана симметричная гауссова функция принадлежности:

• - ( x - b )²

ц(x) = e 2a2 ,(7)

где a – параметр, определяющий ширину функции принадлежности; b – параметр, определяющий положение ядра функции принадлежности. Поскольку в выбранной системе каждому правилу соответстует только одна функция принадлежности выходной переменной, которая является симметричной относительно центра b , то результат дефаззификации для правила (6) будет совпадать с ядром функции принадлежности b .

Алгоритм подстройки основан на вычислении ошибки по принципу работы ПИ-регулятора с ограниченной интегральной составляющей и последующим изменением на её основе параметров консеквента для правил логического вывода [11–13].

Для корректной работы алгоритма необходимо соблюдение следующих ограничений:

• 1.    Для задания выходной переменной используются симметричные гауссовы функции принадлежности, описываемые уравнениями (7).

• 2.    Число функций принадлежности выходных переменных равно числу правил логического вывода и равно произведению числа функций принадлежности разных входных переменных.

• 3.    Центры (ядра) входных функций принадлежности должны быть равномерно расположены на всей области определения. При этом расстояние между центрами функций принадлежности Δ x вычисляется по формуле

• 4.    Значение истинности в точке пересечения двух соседних функций принадлежности x_k равно 0,5: ^ (x k ) = 0,5 . При задании функции принадлежности гауссова типа (6) оценка параметра а , определяющего ширину функции принадлежности, будет рассчитываться по формуле

^A x = ( x max - x min )/ N ^- 1,                                  ⁽⁸⁾

где x max – верхняя граница области определения входной переменной, x min – нижняя граница области определения выходной переменной. В предельном случае для числа функций принадлежности, равным двум, центры функций принадлежности будут совпадать с границами области определения, N – число функций принадлежности.

a = ( b - 0,5 A x )/ j 2|ln0,5| .                                   (9)

Алгоритм основан на изменении ядер функций принадлежности при возникновении ошибки вычислений и состоит из следующих шагов:

• 1.    Берётся набор значений входных переменных [ x 1 , x n ] и соответствующее им расчётное y i и фактическое s i значения выходной переменной ( i – номер шага, на котором было получено прогнозируемое значение на выходе системы нечёткого логического вывода для заданного фиксированного значения входных переменных).

• 2.    Для каждого j -го правила j = [1, M ], где M – число правил в системе, выполняются шаги 3–6.

• 3.    На основе данных, полученных в результате предыдущих измерений, вычисляется значение ошибки для интегральной составляющий по формуле (3).

• 4.    Для уменьшения значения перерегулирования вводится ограничение интегральной составляющей с помощью указания максимального значения Is, выше которого значение интегральной составляющей быть не может:

• 5.    Вычисляется значение пропорциональной составляющей по формуле (4).

• 6.    Вычисляется общее значение ошибки E_i j как сумма пропорциональной и интегральной составляющих

• 7.    Производится корректировка параметра b функции принадлежности заключения j -го правила по формуле

'I = Is, если I > Is, j 4              4                                               (10)

I ij ,      если I ij <  Is .

E ij = K I I ij + K P P ij ,                                         (11)

где K_I и K_p – коэффициенты для интегральной и пропорциональной составляющих, используемые для изменения скорости реагирования на ошибку выхода.

b = b + E j                                (12)

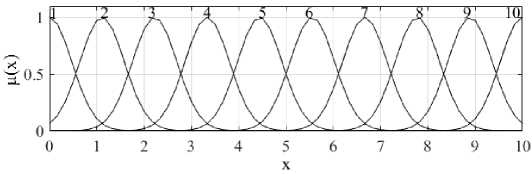
Рис. 1. Графическая интерпретация терм-множества входной переменной

Математика

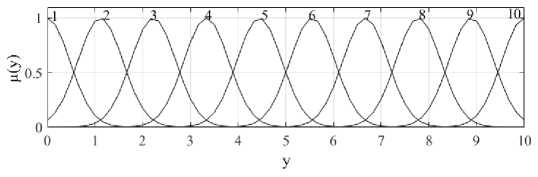
Рис. 2. Графическая интерпретация терм-множества выходной переменной

Рассмотрим работу алгоритма при различных значениях коэффициентов K I и K p для того, чтобы показать их влияние на скорость и точность подстройки параметров модели. Для этого возьмем систему нечёткого логического вывода, содержащую одну входную переменную, терм-множество которой содержит 10 функций принадлежности и одну выходную переменную, терм-множество которой также содержит 10 функций принадлежности (для соблюдения второго ограничения).

Графическое представление терм-множества входной переменной представлено на рис. 1, выходной переменной – на рис. 2. Система будет содержать 10 правил нечёткого логического вывода, посредством которых функция принадлежности входной переменной с номером 1 связана с функцией входной переменной номер 1, функция принадлежности с номером 2 связана с функцией принадлежности выходной переменной с номером 2 и т. д.

Влияние коэффициентов K I и K p будет показано следующим образом: зафиксировано значение входной переменной, равное 3,018. При заданных выше первоначальных настройках системы соответствующее выходное значение будет равно s = 2,7725. На первых 5 шагах задано значение s = 2,7725, начиная с 20 шага задано значение s = 6,0829 (произведено ступенчатое изменение ожидаемой величины). Графики изменения выходного значения y от шага применения алгоритма при различных коэффициентах K I и K p представлены на рис. 3.

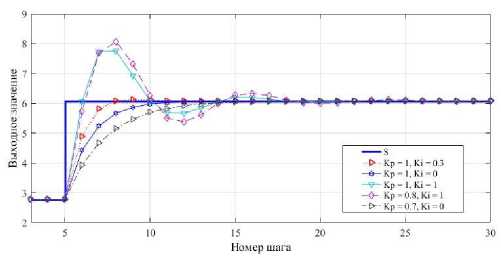
Рис. 3. Зависимость выходного значения системы от шага выполнения алгоритма подстройки при различных коэффициентах K I и K p

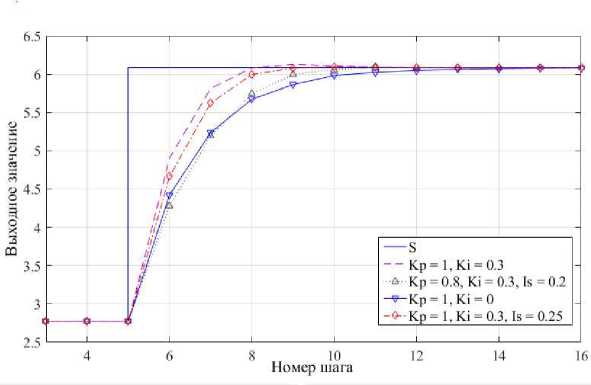
Рис. 4. Зависимость выходного значения от шага выполнения алгоритма подстройки при различных значениях коэффициентов K I , K p , Is

При значениях коэффициента интегральной составляющей больше 0,5 амплитуда перерегулирования становится большой – может превысить 0,7 от значения изменения отслеживаемой выходной величины, но при этом интегральная составляющая позволяет быстрее реагировать на возмущающее воздействие (в этом случае сохраняется скорость подстройки, но уменьшается амплитуда перерегулирования) [14, 15]. Графики изменения выходного значения от шага применения алгоритма для различных значений коэффициентов K_I, K_p, Is представлены на рис. 4.

За счёт изменения параметров выходной переменной алгоритм производит интерполяционную подстройку поверхности нечёткого вывода. При этом подстройка производится за счёт сдвига «опорных точек», формируемых центрами функций принадлежности выходных переменных. Рассмотрим изменение поверхности вывода и расположения функций принадлежности входных переменных для следующих значений входной переменной: в которой функция принадлежности принимает значение ц (x ) = 0,5 и происходит пересечение двух функций принадлежности, для этого возьмем x = 2,77, в которой значение функции принадлежности равно ц (x ) = 0,5, возьмём x = 3,33, в которой только одна функция принадлежности с номером 4 активирует правило, для неё µ ( x ) = 1, и промежуточное значение x = 3. Выбранные значения x и их взаимосвязь с функциями принадлежности входной переменной представлены на рис. 5.

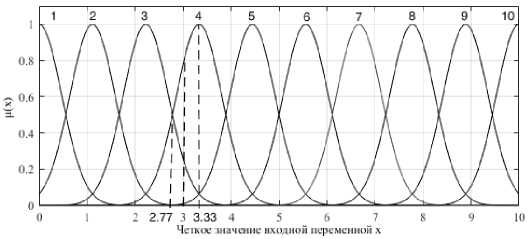
Рис. 5. Выбранные значения x и их взаимосвязь с функциями принадлежности входной переменной

Исходный график поверхности нечёткого логического вывода и его изменения в результате подстройки представлены на рис. 6, изменение расположений функций принадлежности выходной переменной представлены на рис. 7–9.

Рис. 7. Расположение функций принадлежности после подстройки параметров для входного значения 3,33

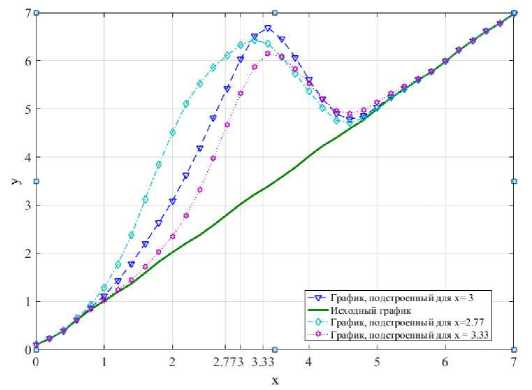
Рис. 6. Изменение поверхности вывода для разных значений входной переменной