Алгоритм оптимального управления замкнутой системой рынка труда на заданном временном интервале

Соотношение спроса и предложения на рынке труда – один из важнейших критериев эффективности функционирования экономической системы на макроуровне. Участником процесса создания продуктов как объектов товарооборота государства является трудоустроенное население, которому, в свою очередь, можно противопоставить безработных. Решение вопросов управления и прогнозирования динамики кадров на рынке труда влияет на качество функционирования всей экономики в целом, поэтому они никогда не теряют своей актуальности.

Например, в [1, 2] осуществлён всесторонний обзор проблемы текучести кадров на рынке труда. В работах [3, 4] исследуются математические закономерности текучести кадров на рынке труда – этот вопрос перекликается с настоящим исследованием. Также с настоящим исследованием перекликается теория коллективной текучести кадров, где анализируется соотношение количества ушедших работников с их качеством (квалификацией) [5]. Что касается работ, посвящённых вопросам оптимального управления рынка труда, то в [6] к стохастической дифференциальной модели рынка труда из [7] применён аппарат оптимального управления.

Для предложенной авторами в [8, 9] конечномерной детерминированной математической модели рынка труда в [10] также сформулирована и решена задача оптимального управления. Здесь предлагается задача оптимального управления замкнутым детерминированным рынком труда в пространстве кусочно-постоянных функций на конечном временном интервале [11]. В общем виде задача кусочно-непрерывного управления объектом, описываемым системой нелинейных дифференциальных уравнений, формулируется следующим образом [12].

Пусть состояние управляемого объекта определяется задачей Коши: X ( t ) = f ( x , u , t ), t e (0; T ],

х (0) = x о , где х = х ( t ) e R n , t e [0; T ] - фазовое состояние объекта; управление u = u ( t ) e R m постоянно на каждом полуинтервале ( t j - 1 ; t j ], j = 1, p , полученном разбиением отрезка [0; T ] на p полуинтервалов, т. е. [13]: u ( t ) = k j = const , k j e R m , t e ( t j _ 1 ; t j ], t о = 0, t_p = T ; функционал качества I j = I ( u ( t ), X j ( t )) на каждом полуинтервале. Задача заключается в нахождении кусочно-постоянных

p значений управления u (t), при которых функционал качества J = ^ I(u (t), xj (t)) ^ max при огра-j=1

ничениях типа равенств: F ( u ( t ), x ( t ), , x ( t )) = 0, x ( t j _ 1 ) = X j _ 1* x ( t j ) = X j ** и неравенств: | u ( t ) | < u * , t e [0; t p ].

Для общего случая условие существования экстремали и условие экстремума сформулированы в виде теоремы Понтрягина в [14].

В [8] представлена следующая модель замкнутого рынка труда:

A - M j a i (t)

^a i⁽ t ) =------- N------ ( y i ⁽ t ) + ^{k P} 1⁽ t ) ) ,

A - M j a i ( t )

^{a n (} t ) = —N— ( y ^{n (} t ) + ^{k P n (} t ) ) ;

в - m j p i (t)

P i ( t ) =------- N------ ( y i ( t ) + * P 1 ( t ) ) - k P 1 ( t),

B - M j P i (t)

P n ( t ) =------- N ¹------ ( y n ( t ) + k P _n ( t ) ) - k P _n ( t );

G - M j 7 i (t)

7 1⁽ t ) =-------^------ ( y i ⁽ t ) ^{+ k P} 1⁽ t ) ) ^- 7 1⁽ t ),

n

G - M j 7 i ( t )

i = 1

^Y n ⁽ t ) = ------- N------- ( y n ⁽ t ) + £ ^p n ⁽ t ) ) ^- 7 n ⁽ t ^).

при условии nnn j«i(t) .Vpi(t) + jYi(t) . 1;

i = 1             i = 1             i = 1

ai (t) g[0;1];

P i ( t ) е [0;1];

7 i (t) g[0;1];

. k i g (0;1].

Здесь A – общее число специалистов высокой категории на рынке труда; В – общее число специалистов средней категории на рынке труда; G – общее число специалистов низкой категории на рынке труда; M – общее число рабочих мест, занятых на предприятии; N – общее число безработных на рынке труда; q – количество подразделений предприятия; k i – коэффициент селекции [15, 16]. Далее a i ( t ) - доля специалистов высокой категории i -го подразделения среди всех трудоустроенных субъектов рынка труда; P i ( t ) - доля специалистов средней категории i -го подразделения среди всех трудоустроенных субъектов рынка труда; 7 i ( t ) -доля специалистов низкой категории i -го подразделения среди всех трудоустроенных субъектов рынка труда. Отметим, что a i ( t ), P i ( t ), 7 i ( t ) - неизвестные функции, тогда как A , B , G , M , N , n , k i – целые.

В [10] решена задача управления для замкнутого рынка труда, где k = const на всём временном отрезке t е [0; T ]. Рассмотрим случай, когда k = к(t ) - кусочно-постоянная функция, заданная таблично для p промежутков времени:

k ˆ ( t )	k ˆ 1	ˆ k 2		ˆ k p
t	[0; t 1 ]	( t 1; t 2]		( t p - 1 ; t p ]

где k j е (0,1], j = 1, p . Тогда система (1) примет вид:

n

A - M ja ij(t)

i = 1

^а 1 j ⁽ t ) =-------- n --------( у х j ⁽ t ) + ^kj ⁽ t ^{) p} 1 j ⁽ t ) ) ,

A ^- M j ^a ij ⁽ t )

^а nj ⁽ t ) =-------- N------- ( y nj ⁽ t ) + ^kj ⁽ t ^{) p} nj ⁽ t ) ) ;

в - m j p ij (t)

Ру ( t ) =-------- N -------( Y 1 j ( t ) + k j ( t ) P 1 j ( t ) ) - k j ( t ) P 1 j ( t ),

B - M j p ij (t )

P nj ( t ) =-------- N------ ( y nj ( t ) + k j ( t ) P nj ( t ) ) - k j ( t ) P nj ( t );

G - M jb y ij ( t )

7 1 j ⁽ t ) =-------- i N 1------- ( Y 1 j ⁽ t ) ⁺ kt j ⁽ t ^{) p} 1 j ⁽ t ) ) ^- Y 1 j ⁽ t ),

G - M j y _y-( t )

⁷ nj ⁽ t ) =-------- N =1------- ( y nj ⁽ t ) ⁺ kt j ⁽ t ^{) P} nj ⁽ t ) ) ^- Y nj ⁽ t ).

при условии nnn

ja j( t) + jPj( t) + jYj( t) ^ 1, i = 1             i = 1             i = 1

'a ij ⁽ t ) e ^[ 0;1 ^] ;

P ij ( t ) е [0;1];

Y ij ( t ) е [0;1];

_ k j е (0,1]

для каждого из p промежутков времени ( j = 1, p ).

Пусть k ^ˆ ( t ) описывается функцией (4). Тогда

• •    управление u ( • ) = k ( t ), где k е (0; 1];

• •    функции состояния системы на j -м промежутке времени ( j = 1, p ):

^xj ( ■ ) = ^{( a} i j (t ), - , ^а nj (t ), ^e i j (t ), - , ^e nj (t ), Y i j ( ¹ ), •- , y nj (t));

• •    функционал качества управления системой на j- м промежутке времени ( j = 1, p ):

I(u,xj)=rαjσαj(k,t)+rβjσβj(k,t)+rγjσγj(k,t), где n  nn o σαj =∑αij(kj,t), σβj =∑βij(kj,t), σγj =∑γij(kj,t);

i = 1                             i = 1                             i = 1

o r _{α j} , r _{β j} , r _{γ j} – коэффициенты качества [10].

p

На каждом из p временных промежутков найти k = k_j ^* такое, что ∑ I ( u , x_j ) → max при ог- j = 1

раничениях типа равенств (5) и (6) и неравенств (7).

В силу единственности оптимального управления для каждого из p временных промежутков, показанной в [10], задачу максимизации суммы можно решить путём максимизации каждого j- го слагаемого, т. е. уместно использовать жадный алгоритм [17]. Таким образом, задача оптимального управления замкнутым рынком труда с n источниками спроса разбивается на p подзадач, связанных между собой таким образом, что результаты j -й подзадачи являются входными данными для j +1-й подзадачи, поэтому их необходимо решать последовательно для каждой j = 1, p .

Нахождение k ^ˆ ₁ ^* на первом временном промежутке для t ∈ (0; t ₁] осуществляется по аналогии с решением задачи управления замкнутым рынком труда, где k ˆ = const на всём временном отрезке t ∈ [0; T ] , которое приведено в [10]. Значения функций состояния х ₁( ⋅ ) в момент времени t ₁ будут выбраны в качестве исходных значений для нахождения k ^ˆ ₂ ^* на втором временном промежутке и т. д. Решением задачи оптимального управления рынка труда будет функция (4) с найденными значениями в каждый временной промежуток.

• 2. Пример оптимального управления рынком труда
  
  посёлка Сылва Пермского края в течение трёх лет

  По официальным данным [18, 19] рассчитаем текущие значения входных параметров системы (5) для рынка труда посёлка Сылва Пермского края, приняв «гипотезу С» из [15, 16], согласно которой вакантные места считаются занятыми субъектами низкой категории. Отсюда на градообразующем предприятии АО «Пермская птицефабрика» положим r _{α j} = r _α = const, r _{β j} = r _β = const , r _{γ j} = r _γ = 0 и r _α >  r _β >  r _γ . Найдём оптимальное управление рынком труда посёлка Сылва Пермского края в 2024–2026 гг., т. е. на трёхлетнем промежутке, при условии, что для АО «Пермская птицефабрика» k ^ˆ = k ^ˆ ( t ) . Тогда управление u ≡ k ^ˆ ( t ) описывается функцией (4), где p = 3.

Решим последовательно задачи оптимального управления для каждого из трёх временных промежутков, начиная с 2024 года. Аналогично [10] с помощью Wolfram Mathematica построим график I ( u , х ₁) при заданных начальных условиях таких, что значения констант функций состояния системы х ₁( ⋅ ) характеризуют рынок труда посёлка Сылва Пермского края на конец 2023 года [18, 19]. Тогда уравнение ∂ I ∂ k ^ˆ = 0 имеет решение на отрезке k ^ˆ ∈ (0;1] , и ∃ k ^ˆ* ∈ (0;1] : ∀ k ^ˆ ∈ (0;1] / { k ^ˆ* } I ( k ^ˆ* ) >  I ( k ^ˆ ) в момент времени t = t ₁ , показанное на рис. 1.

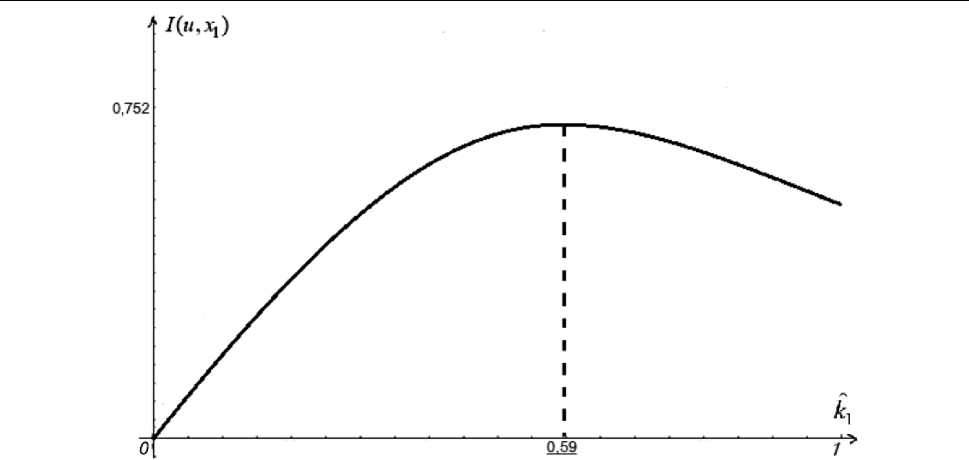
Рис. 1. График функции соотношения «цена – качество» для всех трудоустроенных кадров на рынке труда посёлка Сылва Пермского края на 2024 г.

Fig. 1. Graph of the price-quality ratio function for all employed personnel in the labor market of the village Sylva in the Perm Territory for 2024

Как видно из графика, k 1* = 0,59 .

Следующим шагом построим график I ( u , х ₂) при заданных начальных условиях таких, что значения констант функций состояния системы х 2 ( - ) характеризуют рынок труда посёлка Сылва Пермского края на конец 2024 года при k 1* = 0,59 . Получим график I ( и , х ₂), показанный на рис. 2.

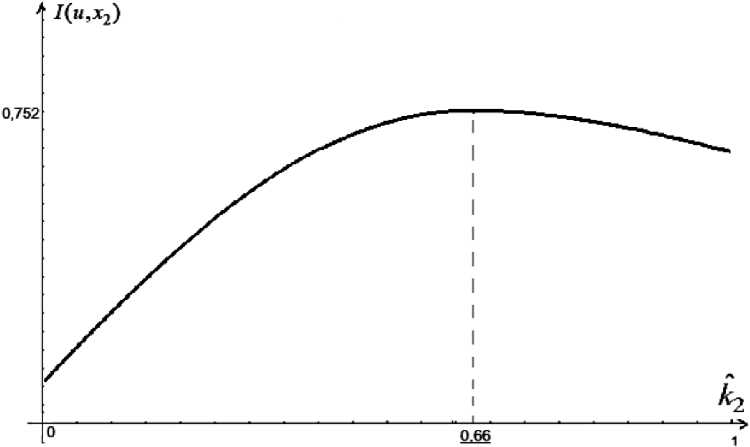
Рис. 2. График функции соотношения «цена – качество» для всех трудоустроенных кадров на рынке труда посёлка Сылва Пермского края на 2025 г.

Fig. 2. Graph of the price-quality ratio function for all employed personnel in the labor market of the village Sylva in the Perm Territory for 2025

Как видно из графика, k ₂ * = 0,66.

Аналогично построим график I ( и , х 3 ) при k ₂ * = 0,66 (рис. 3).

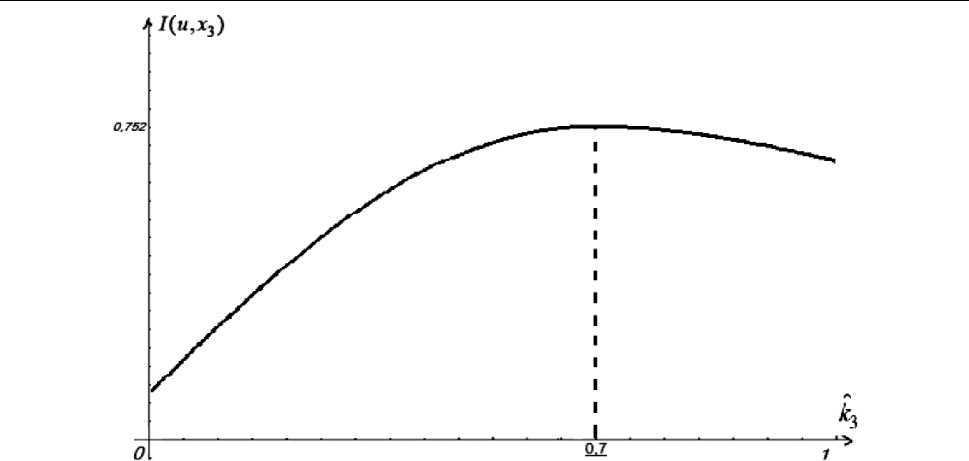
Рис. 3. График функции соотношения «цена – качество» для всех трудоустроенных кадров на рынке труда посёлка Сылва Пермского края на 2026 г.

Fig. 3. Graph of the price-quality ratio function for all employed personnel in the labor market of the village Sylva in the Perm Territory for 2026

Как видно из графика, k ^ˆ ₃ ^* = 0,7 .

Таким образом, функция k ^ˆ = k ^ˆ ( t ) для рынка труда посёлка Сылва Пермского края на промежутке 2024–2026 гг. имеет следующий вид (рис. 4):

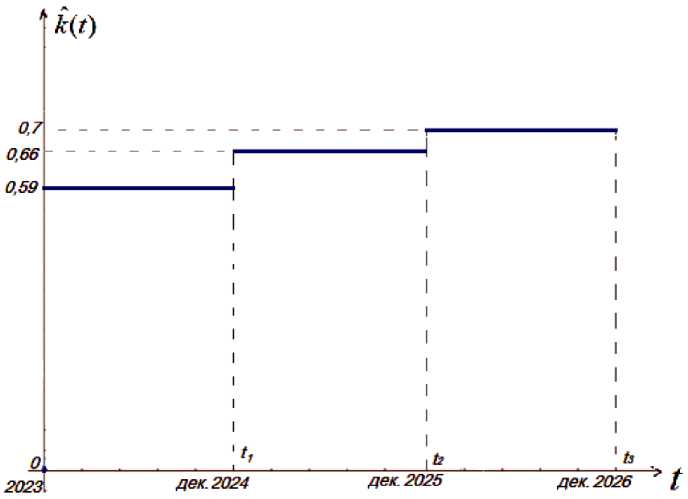
Рис. 4. График функции к = k(t) для рынка труда посёлка Сылва Пермского края на промежутке 2024–2026 гг.

Fig. 4. Graph of the function k = k(t) for the labor market of the village Sylva in the Perm Territory for 2024–2026

k ˆ ( t )	0,59	0,66	0,7
t	[0; t 1 ]	( t 1; t 2]	( t 2; t 3]

Очевидно, значение k ^ˆ _i ^* с каждым годом увеличивается. Такое поведение функции k ^ˆ ( t ) объясняется тем, что при r _a >  r ^ >  r максимизация функционала соотношения «цена - качество» на рынке труда в общем случае подразумевает увеличение коэффициента селекции [10].

Таким образом, оптимальное управление рынком труда посёлка Сылва Пермского края подразумевает постепенное повышение значения коэффициента селекции на градообразующем предприятии. Учитывая, что на конец 2023 года значение коэффициента селекции АО «Пермская птицефабрика» согласно принятой выше «гипотезе С» [15, 16] равняется 0,44, в будущем году рекомендуется установить более строгие требования к соискателям вакантных должностей.

Для предложенной в [9] модели замкнутого рынка труда коэффициент селекции впервые рассмотрен как кусочно-постоянная функция от времени. Сформулирована и решена задача оптимального управления реально существующим рынком труда посёлка Сылва Пермского края на ближайшие три года при условии, что коэффициент селекции градообразующего предприятия меняется каждый год, а коэффициенты качества остаются константами.

В дальнейшем коэффициенты качества также возможно рассмотреть как функции от времени, поскольку усреднённая оплата труда по субъектам всех трёх уровней квалификации в разрезе нескольких лет может меняться как минимум с поправкой на инфляцию и индексацию заработной платы.