Алгоритм оптимизации вибрационных нагрузок, формируемых зубчатыми зацеплениями перспективной коробки передач грузового автомобиля

Производители транспортных машин разрабатывают новые конструкции с учетом повышающихся требований потребителей к различным эксплуатационным характеристикам, показателям надежности и др. Одним из важнейших требований является обеспечение высокой комфортабельности, определяемой, в первую очередь, уровнем виброакустического излучения (шума) [1, 2].

Общие методы и подходы к снижению вибрационного и акустического излучения, производимого элементами энергосиловых установок, известны и широко применяются в процессе отработки конструкций. Однако значительные успехи в создании экономичных и малошумных энергосиловых установок (тепловых, гибридных, электрических) заставляют инженеров и ученых обратить свое внимание на совершенствование трансмиссий, вклад которых в интегральный уровень виброакустического излучения становится все более существенным [3–4].

При этом многие современные исследователи акцентируют свое внимание на снижении расхода топлива [5], повышении долговечности элементов конструкции [6–8], разрабатывают и предлагают методы снижения воздействующих на трансмиссию крутильных колебаний за счет оптимизации модальных характеристик энергосиловых установок. Для этого совершенствуются существующие и разрабатываются новые конструкции гасителей крутильных колебаний – двухмассовые маховики (Dual Mass Flywheel (DMF)), центробежные маятниковые поглотители (Centrifugal Pendulum Absorber (CPA)) и др.

В последние годы прилагаются [9–10] значительные усилия для анализа передач на системном уровне с целью достижения лучших характеристик с точки зрения обеспечения требуемого уровня виброакустического излучения (шума). Основная задача состоит в том, чтобы исследовать динамику системы достаточно подробным, но в то же время эффективным с вычислительной точки зрения способом. Факторы, формирующие виброакустическую активность трансмиссии, определяются параметрами конструкции зубчатых передач и модальными характеристиками корпуса [10–12], взаимодействующими между собой через подшипниковые опоры.

Основным подходом является вычисление динамики на системном уровне с использованием конечно-элементного моделирования системы, включающей шестерни, подшипники, валы и корпус. Все элементы взаимосвязаны и важны для обеспечения точных результатов моделирования.

В соответствии с общепринятой классификацией акустическое излучение коробок передач подразделяется на три вида: Gearwhine, rattle и clunk. Rattle и clunk возникают вследствие несовершенства динамической системы или системы управления. Технические решения по исключению данных нежелательных эффектов строятся на основе оптимизации упруго-инерционных характеристик динамической системы с использованием дискретных математических моделей (multibody моделирование).

Основной причиной проявления Gearwhine является переменная жесткость в зубчатом зацеплении, возникающая вследствие кинематической погрешности (в англоязычной литературе – Transmission Error (TE)), приводящей к генерации высокочастотных вибраций картера трансмиссии, порождающих, в свою очередь, нежелательное акустическое излучение. Нейтрализация данного явления – решение задачи оптимизации виброакустических характеристик динамической системы наиболее эффективно с применением комплекса современных программно-аппаратных средств на основе методов расчетно-экспериментального модального анализа [9, 12].

Целью данного исследования является решение первой части сформулированной выше задачи – разработка цифровой копии перспективной автоматической коробки передач для шоссейного грузовика категории N2 и оптимизация зубчатых зацеплений.

Представленные материалы являются частью работы по созданию верифицированной математической модели перспективной автоматической коробки передач, которая должна адекватно описывать ее виброакустическое поведение в процессе эксплуатации.

В первой части статьи описано создание цифровой копии трансмиссии в программном продукте Simcenter 3D Motion Trasmission Builder [13] для определения нагрузок в опорах. Применение наиболее современного софта позволило существенно сократить время создания модели по сравнению с более ранними работами коллектива авторов за счет автоматизациизадания многотельных систем.

Во второй части приводятся результаты определения оптимальных параметров зубчатых колес по критерию минимизации кинематической погрешности передачи в программном продукте KISSsoft, созданном для проектирования коробок передач.

Моделирование АКП

На рис. 1 представлена кинематическая схема и разрез рассматриваемой коробки передач.

Процесс создания цифрового двойника исследуемой трансмиссии начинается с настройки компоновки: размещения валов, зубчатых колес и подшипников и определения параметров зубчатых зацеплений.

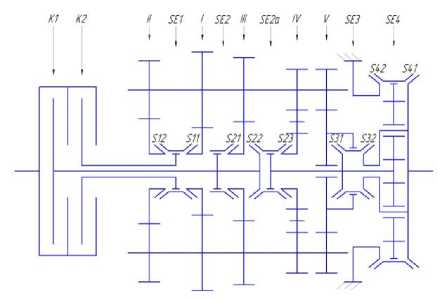
а

Рис. 1. Кинематическая схема (а) и разрез коробки передач (б)

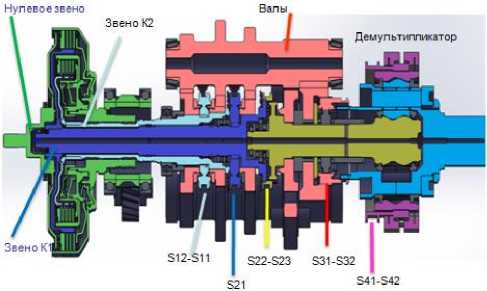
б

Затем выполняется расчет геометрии шестерен на основе стандарта ISO 21771 и построение трехмерных геометрических моделей, для которых автоматически задаются начальные и граничные условия: начальные углы компонентов трансмиссии, включая фазирование зубчатых колес, соединения и ограничения. После создаются модели контакта зубчатых колес. Основной сложностью при этом является учет изменяющейся во времени силы зацепления. На данный момент существует три решения.

• 1.    Сила зацепления вычисляется на основе контактной теории Герца. В этом методе учитывается только контактная деформация, эффект выступающего луча зубьев не учитывается, а амплитуда силы зубчатого зацепления чувствительна к параметрам контакта.

• 2.    Метод нестационарных конечных элементов. Этот метод точен в решении контактного усилия, но вычислительные затраты велики, поэтому для выполнения инженерных расчетов данный метод редко используется.

• 3.    Сила зацепления шестерни в направлении линии зацепления рассчитывается с помощью нелинейной пружинно-демпфирующей системы. Этот метод основан на динамике зубчатой передачи, жесткость пружины может изменяться. Этот метод является эффективным, а результаты заслуживают доверия.

Авторы K. Umezawa [14], Y Cai [15–16], LI-RunFang [17] представили собственные модели определения жесткости в зубчатом зацеплении. Функция определения жесткости в зацеплении, предложенная в работах [15–16], наиболее точно совпадает с результатами экспериментальных исследований. В этом случае основной задачей является определение контакта, вычисление деформации зубьев и преобразование ее в нагрузки.

Simcenter 3D Motion Trasmission Builder предлагает три метода для преобразований деформаций в нагрузки: стандартный (на основе стандартов ISO с вводом дополнительных данных), аналитический (ISO + CAI) и расширенный (эмпирический или конечно-элементный препроцессор).

Для решения задачи исследования был выбран аналитический метод, так как именно он рекомендован для исследований NVH поведения. Он позволяет зафиксировать «вой» (Gear whine) из-за изменяющейся во времени жесткости зацепления. Также этот метод позволяет сделать существенный шаг вперед по сравнению со стандартным методом и является более простым и быстрым по сравнению с расширенным. Используемая здесь функция сочетает определение жесткости по ISO [18] со специальными формулами, разработанными для определения изгибной жесткости для прямозубых и косозубых шестерен[15–16].

Изображение полной имитационной модели кинематической части исследуемой трансмиссии представлено на рис. 2.

Упруго-инерционные характеристики задавались исходя из геометрических характеристик тел и их материалов. Внешние нагрузки на коробку передач моделировались переменными значениями скорости вращения входного вала и переменным значением моментов на насосном и выходном валах, определенными в соответствии с типовыми режимами нагружения машин соответствующего класса.

Рис. 2. Имитационная модель кинематической части исследуемой трансмиссии

Модель кинематической части исследуемой трансмиссии интегрировалась в верифицированную конечно-элементную упругую (flexible) модель корпуса АКП. После чего запускалась симуляция всех рассматриваемых режимов работы АКП для получения нагрузок, необходимых для определения виброакустического поведения трансмиссии.

Оптимизация зубчатого зацепления

При изготовлении абсолютно жестких зубчатых колес без погрешностей и модификаций шестерни имели бы постоянную скорость и идеально передавали крутящий момент. При постоянных силах в зубчатом зацеплении не могут возникнуть вибрации и шум, которые, в свою очередь, передавались бы на валы через подшипники и опоры на корпус коробки передач. Следовательно, можно сделать вывод, что основной причиной возникновения вибраций и повышенного акустического излучения коробок передач является кинематическая погрешность, которая является критерием качества зубчатых колес.

Кинематическая погрешность - задержка вращения между ведущей и ведомой шестернями, вызванная упругой деформацией, погрешностями при производстве (обработка резанием и зубофрезерование) и сборке. Принятое определение - разница между фактическим положением ведомой шестерни и положением, которое она занимала бы при идеальном изготовлении. Кинематическая погрешность передачи исчисляется в линейных величинах - длиной дуги делительной окружности ведомой шестерни. Характеристика кинематической погрешности зависит от состояния зацепления зубчатых пар в конкретный момент времени. Ранее контрольное измерение кинематической погрешности проводилось на зубообкатных приборах, но с развитием технологий необходимость ее контроля на этапе постизготовления отпала. Современные вычислительные модули программ позволяют с высокой точностью прогнозировать этот показатель зубчатого зацепления на каждом угловом шаге сопряжения.

В процессе эксплуатации изменение жесткости зубчатого зацепления определяют изменением длины линии контакта и деформации зубьев. Поэтому прогнозирование ошибки передачи является необходимым условием для снижения уровня вибраций корпуса и шума, излучаемого коробкой передач. Для исследования этого феномена многими исследователями применяется трехмерный конечно-элементный анализ деформаций зубчатых колес с использованием различных моделей и решателей.

В связи с значительными затратами вычислительных мощностей при реализации конечноэлементных методов на данном этапе работы в качестве инструмента для проведения анализа влияния параметров зубчатых колес на ошибку передачи и на их оптимизацию был выбран программный продукт KISSsoft [19].

KISSsoft – это модульная программа расчета для определения размеров, оптимизации и проверочных расчетов деталей машин согласно международным стандартам. Для сборки в программе вально-планетарной коробки передач использовался программный блок KISSsys. На рис. 3 показана собранная модель исследуемой автоматической коробки передач.

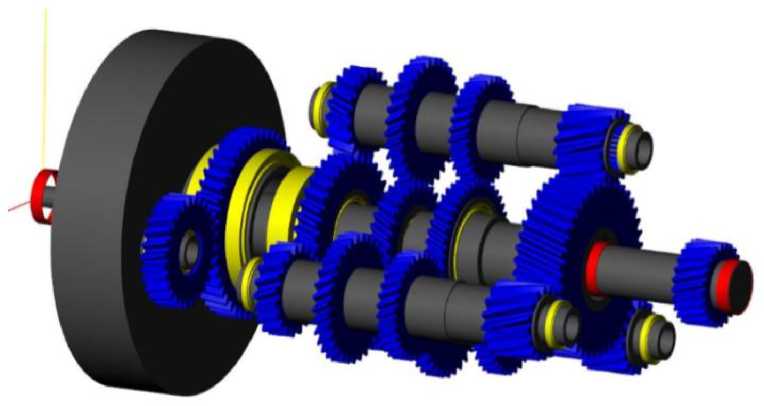
Рис. 3. Собранная модель исследуемой автоматической коробки передач

Широкий выбор параметров зубчатых колес, материалов изготовления, видов смазок, допусков, режимов нагружения, требуемого срока службы и т. д., позволяет полноценно и достоверно моделировать зубчатые зацепления. Особенностью программного модуля KISSsys является тот факт, что в построенные модели зубчатых колес закладывается также погрешность изготовления, например, биение режущего инструмента, биение заготовки, колебания станка и т. д.

Программный блок KISSsys проводит прогнозирование кинематической погрешности по следующему алгоритму:

• 1.    Выполняется последовательный поворот сопряженных колес на величины равные угловым шагам ведущего и ведомого колес. Величины угловых шагов поворотов зубчатых колес принимаются в зависимости от принятого количества точек отсчета кинематической погрешности за один оборот ведомого колеса. Таким образом, чем больше точек углового положения колеса зафиксируется при прогнозировании, тем более высокую точность выходной информации о дефектах зубчатых колес будет содержать визуализация кинематической погрешности (сплайн-кривая).

• 2.    Высчитывается угловой шаг поворота входного зубчатого колеса в зависимости от передаточного отношения, определяемого делением числа зубьев ведущего колеса на число зубьев ведомого. Ввиду присутствия поэлементной неточности, элементарных погрешностей ведомое колесо поворачивается не на расчетный угол, а на действительный. При этом в модели происходит либо увеличение зазора, либо пересечение геометрии зубчатых колес. И то и другое на реально существующих зубчатых передачах производит пагубное воздействие. Определение действительного угла поворота производится путем решения углового положения зубчатого колеса, при котором отсутствовало бы геометрическое пересечение профилей зубьев, расстояние же между рабочими профилями зубьев обоих колес ищется минимальным (принимается касание профилей друг друга).

Таким образом, реализация приведенного выше алгоритма позволила определить массив значений разницы между действительным и расчетным углом поворота ведомого зубчатого колеса – массив значений кинематической погрешности.

Кинематическая погрешность зависит от передаточного отношения. Но при задачах оптимизации виброакустических показателей изменение передаточного отношения не представляется возможным. Поэтому наиболее действенный метод снижения кинематической погрешности – увеличение угла наклона зубьев косозубых передач (β). При выполнении расчетов ограничением является неизменность заложенного в проекте межосевого расстояния посредством правильного выбора коэффициентов смещения (χ1 и χ2) [20].

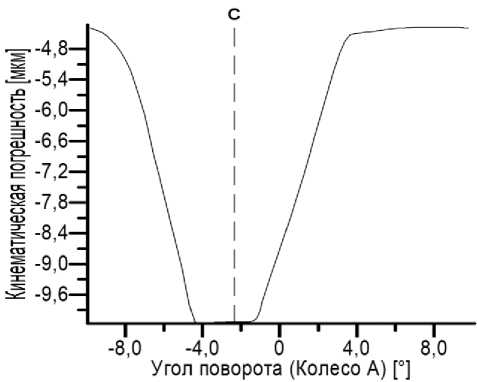
Для каждого зубчатого зацепления были увеличены углы наклона зубьев. Минимальное увеличение составляло 1,6 градуса наклона, максимальное – 12. Из всех подходящих вариантов коэффициентов смещения предпочтение определялось функциональным назначением коробки передач. Результаты определения показателей кинематической погрешности в зубчатых зацеплениях АКП сведены в таблицу. На рис. 4 показана визуализация результатов оптимизаций зубчатых колес путем сравнения сплайн-кривых показателей кинематической погрешности.

Показатели кинематической погрешности в зубчатых зацеплениях АКП

Зацепление Кинематическая погрешность, μm Исходный вариант Оптимизированный вариант Привод насоса 9,9 9,0 Первый ряд 10,1 7,6 Второй ряд 9,1 8,5 Третий ряд 10,3 9,1 Четвертый ряд 17,3 17,0 Пятый ряд 4,2 4,1 а                                                  б

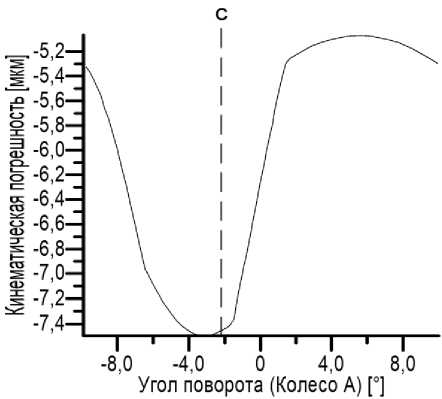
Рис. 4. Кривые кинематической погрешности зубчатого зацепления первого ряда: а – исходный вариант, б – оптимизированный вариант

Заключение и выводы

По результатам проведенных исследований можно сделать следующие выводы.

• 1.    На основе применения комплекса современных программно-аппаратных средств разработан и реализован алгоритм определения и оптимизации нагрузок, формируемых в зубчатых зацеплениях и передаваемых на корпус трансмиссии.

• 2.    Разработан цифровой двойник перспективной автоматической коробки передач грузового автомобиляв программном продукте Simcenter 3D Motion Trasmission Builder, который позволит при выполнении дальнейших вычислительных экспериментов оценить качество выполнения зубчатых зацеплений в проектируемой коробке передач, а также определить уровень нагрузок, передаваемых на картер трансмиссии.

• 3.    Получены результаты определения оптимальных параметров зубчатых колес по критерию минимизации кинематической погрешности передачи (TE) в программном продукте KISSsoft. Для зубчатых зацеплений отдельных рядов коробки передач кинематическая погрешность снижена до 30 %.