Алгоритм планирования энергосберегающей параллельной обработки информации с учетом информационной важности и времени поступления задач

Современное состояние сетевых технологий характеризуется широким внедрением мобильных вычислительных сетей. Отличительные свойства данных сетей состоят в том, что они имеют большое число различающихся по производительности элементов (вычислительных устройств), обменивающихся данными по ненадежным каналам с переменной пропускной способностью, объединены в общий ресурс, характеризуются сложной зависимостью производительности от режимов энергопотребления и характеристик каналов связи, а также изменением структуры в процессе функционирования. В данных сетях имеет место зависимость взаимного положения узлов на скорость обработки данных. Расширение масштабов использования мо- бильных неоднородных вычислительных сетей влечет необходимость повышения автономности их функционирования [1; 2]. Перенос решения ряда задач со стационарных на мобильные вычислительные средства приводит к необходимости увеличения производительности отдельного мобильного компьютера и совершенствование подходов к построению и организации функционирования мобильной вычислительной сети в целом. Наращивание производительности вычислительного устройства мобильного компьютера вступает в противоречие с ограничениями по массе, энергозатратам, требованиям по надежности. При этом наращиваемые ресурсы мобильного компьютера не будут использованы в полной мере, а будут востребованы лишь на относительно коротких интервалах его функционирования.

Решением данного противоречия является подход, в основу которого положена технология предоставления информационно-вычислительных ресурсов на основе модели «клиент- сервер» с конфигурацией «тонкий клиент». Данный подход позволяет минимизировать требования к аппаратно-программным ресурсам компьютера-клиента, перенося часть информационно-вычислительной нагрузки на центры обработки данных (серверы). При организации распределенной обработки информации в мобильной неоднородной вычислительной сети возникает задача оптимального распределения вычислительной нагрузки и планирования обработки информации между клиентом и сервером при ограниченном энергоресурсе бортовых источников питания [3].

Стратегия планирования предлагаемого алгоритма основывается на прогнозировании загрузки процессоров, предсказании динамики поступления задач и возможных задержек, связанных с передачей данных в каналах связи, с использованием предыдущего опыта обработки информации согласно результатам предыдущего планирования. Основной задачей прогноза является оценка общего времени выполнения заданий и минимизация их количества при задействовании минимального числа процессоров.

Оценка задержек поступления задач вычисляется на основе статистических сведений, накопленных по результатам предыдущих обработок информации. В основу прогноза могут быть положены методы обучения на примерах, известных из исследований в области искусственного интеллекта. Статистика, полученная после выполнения плана, сохраняется, и производится пересчет задержек поступления задач.

Концепция алгоритма планирования. В предлагаемом полиноминальном эвристическом алгоритме можно выделить три основных этапа. На первом – формируется массив обрабатываемых входных задач и рассчитывается их удельная стоимость. Затем на втором – производится назначение задач на процессоры в последовательности, начиная с задачи, имеющей максимальную удельную стоимость [4]. Планирование осуществляется начиная с первого процессора, чтобы максимально загрузить его до директивного времени завершения вычислений. Если после загрузки процессора остались нена-значенные задачи, то производится перераспределение, включая в расписание второй процессор. Планирование происходит до тех пор, пока не будут распределены все задачи массива или не будут задействованы все процессоры. Это позволяет обеспечить минимальное число задействованных процессоров при обработке заданий за счет их максимальной загрузки, что снижает энергопотребление вычислительного процесса.

На третьем этапе определяется суммарная важность для полученного варианта планирования и сравнивается с требуемой. Если условие не выполняется, то из обработки исключается задание с минимальной важностью, и алгоритм повторяется, начиная с первого этапа.

Исходные данные для алгоритма:

• 1)    w_i – важность i -й задачи;

• 2)    t_i – время выполнения (длительность) i -й задачи;

• 3)    T _д – директивное время завершения вычислений;

• 4)    k – количество задач;

• 5)    A f i - погрешность времени поступления задачи (задержка по накопленной предыдущей статистике);

• 6)    N – количество процессоров;

• 7)    τ_i – планируемое время поступления (раннего начала выполнения) задачи.

Требуется: произвести назначение задач на множество процессоров (процессорных модулей) вычислительной системы с учетом возможных задержек поступления заявок на обработку и определить значения двоичных коэффициентов α_ij и количество задействованных процессоров n^* , обеспечивающее выполнение условия:

*       *

k n

• УХ^С/ . ■ wi > ^max,

i = 1 7=1

n * >  min,                              (1)

k ■ max£a • (t + A^. +1,) < T, Vj = 1,..,n*.

i = 1

ВЕСТНИК 2017

Предполагается, что изначально минимально необходимое число процессоров неизвестно, и оно определяется в процессе назначения. Далее проблема формулируется как поиск среди возможных такого варианта назначения на процессоры, который близок к рациональному по критерию, представленному взвешенной суммой числа использованных процессоров и суммарной важностью задач [5].

Ограничения . Необходимо, чтобы длина расписания не превышала установленного директивного срока обработки T _д задач, при этом задействовав минимальное число процессоров.

Общая структура алгоритма представляется в следующем виде.

Шаг 1 . Формирование массива обрабатываемых задач:

G = {1,…, k^* }. (2)

На первой итерации алгоритма задействованы для планирования обработки все входные задачи k^* = k .

Шаг 2 . Инициализация (обнуление) матрицы α = { α_ij } задействованных i задач на j процессорах, где:

• 1 1,    если будет обрабатываться на j процессоре , «и = 1

[ 0, если не будет обрабатываться на j процессоре.

Шаг 3 . Инициализация количества используемых процессоров n^* . На первой итерации алгоритма используется один процессор n : = 1.

Шаг 4 . Вычисление удельной «стоимости» λ _i каждой i- й задачи:

λ i = ^wi .                   (3)

ti

Шаг 5 . Перенумеровывание задач согласно правилу:

λ1≥λ2≥λ3≥…≥λk*.

Шаг 6 . Назначение множества задача G на n^* процессорах.

Шаг 6.1 . Распределение задач по n^* процессорам, начиная с первого процессора по правилу:

ВЕСТНИК 2017

'2 = max ‘/J.

* Т = min О. 1 Ar.), т,+ \т +t,< Тд.

После назначения задачи соответствующий элемент матрицы приравнивается к 1: α_ij = 1.

Шаг 6.2 . Проверка массива обрабатываемых задач G.

Если назначены все задачи массива G на n* процессоров, то формируем расписание Ψ (рис. 1) и переходим к шагу 9, иначе переходим к шагу 6.3.

Шаг 6.3 . Проверка количества задействованных процессоров n^*.

Если число процессоров n* = N, то переходим к шагу 7, иначе увеличиваем число используемых процессоров n*:=n*+1 и переходим к шагу 6.1.

Планирование начинается с первого процессора, чтобы максимально загрузить его до директивного времени завершения вычислений. Если после загрузки процессора остались неназначен-ные задачи, то производится перераспределение с подключением второго процессора. Планирование происходит до тех пор, пока не будут распределены задачи массива G .

Шаг 7 . Коррекция массива обрабатываемых задач G : исключение задачи с минимальной важностью min{ w_i }.

Если важность задач одинакова, то исключается задача из массива G с max ( г , + A f i ) .

Шаг 8 . Формирование нового массива обрабатываемых задач G = {1,…, k^* } и переход к шагу 2.

Шаг 9 . Расчет суммарной важности обрабатываемых задач:         _k *

W ^* = ∑ α _ij ⋅ w_i ,              (5)

i = 1

где k^* – количество используемых для обработки задач согласно массиву G .

Шаг 10 . Проверка составленного плана на максимальность суммарной важности обрабатываемых задач.

Если W^* ≥ W , то выдается матрица двоичных коэффициентов α_ij и количество процессоров n^* , иначе : исключается задача с min w_i и max t_i , переходим к шагу 2.

На первой итерации алгоритма считается W^* = W .

Выходные данные алгоритма:

α_ij – массив задействованных задач;

n^* – количество задействованных процессоров;

W – суммарная важность обработанных задач (определяет результативность);

Ψ – план обработки задач.

Пример составленного расписания обработки k^* задач на n^* процессоров показан на рис. 1.

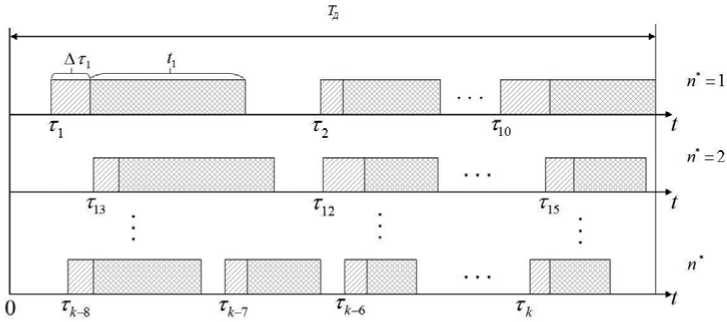
Рис. 1. Пример расписания

Энергосбережение разработанного алгорит- задач. При случайном формировании любого за- ма заключается в использовании минимального числа задействованных процессоров при обработке задач за счет их максимальной загрузки, что обеспечивает снижение общего энергопотребления вычислительного процесса.

Исследование эффективности предложенного алгоритма планирования осуществлялось путем сбора статистики с использованием разработанной программы случайной генерации примеров заданий [6]. Для каждого количества процессоров генерировалось по 1 000 примеров

Зависимость среднего значения погрешности планирования от количества обработанных задач

Таблица 1

Число задач	Кол-во ВМ n = 2	Кол-во ВМ n = 3	Кол-во ВМ n = 4	Кол-во ВМ n = 5	Кол-во ВМ n = 6	Кол-во ВМ n = 7	Кол-во ВМ n = 8
10	0,9293	0,9308	0,9407	0,9407	0,9465	0,9472	0,9495
20	0,9552	0,9493	0,9462	0,9459	0,9488	0,9520	0,9582
30	0,9641	0,9570	0,9550	0,9533	0,9527	0,9543	0,9600
40	0,9691	0,9629	0,9600	0,9584	0,9589	0,9596	0,9607
50	0,9725	0,9668	0,9641	0,9621	0,9612	0,9604	0,9604
60	0,9749	0,9697	0,9671	0,9649	0,9636	0,9636	0,9634
70	0,9768	0,9722	0,9692	0,9671	0,9662	0,9650	0,9658
80	0,9784	0,9740	0,9711	0,9690	0,9678	0,9669	0,9677
90	0,9797	0,9756	0,9727	0,9706	0,9693	0,9690	0,9692
100	0,9807	0,9768	0,9739	0,9721	0,9709	0,9697	0,9495

ВЕСТНИК 2017

На рис. 2 представлен график зависимости график зависимости среднего значения погреш-

среднего значения погрешности разработанного ности планирования от количества задейство-

алгоритма планирования от количества обрабо- танных заданий в промежутке {10, 95} при раз- личном количестве задействованных вычисли-   {10, 80}.

тельных модулей {2, 8}. На рис. 3 представлен

дания сначала производилась генерация времени его прихода на обработку. Далее для каждой задачи путем случайной генерации формировались длительность выполнения и погрешность времени ее поступления как реализации случайной величины, равномерно распределенной в некотором интервале. Результаты модельного эксперимента, отражающие долю испытаний, в которых алгоритм дал оптимальный результат, представлены в табл. 1.

ванных вычислительных модулей {2, 8} при различном количестве обрабатываемых заданий

0,9780

| 0,9680

^ 0,9580

т 0,9480

5 0,9380

0,9280

10 15 20 25 30 35 40 45 50 55 60 60 65 70 75 80 85 90 95

Количество выполняемых заданий

Количество задействованных _w —п=2 —п=3 —п=4 —п=5   п=6 —п=7 —п=8

вычислительных модулей

Рис. 2. График зависимости среднего значения погрешности планирования от количества обработанных задач

ВЕСТНИК 2017

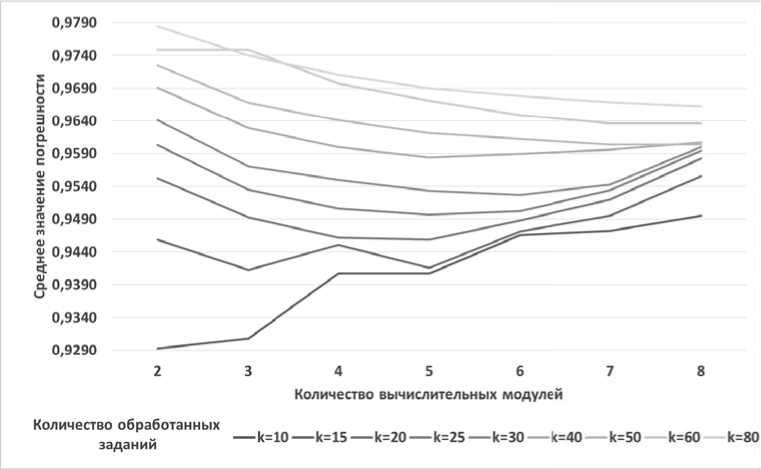
Рис. 3. График зависимости среднего значения погрешности планирования от количества задействованных вычислительных модулей

Сравнительный анализ показал, что погрешность разработанного алгоритма планирования не превышает 8% от алгоритма полиномиальной сложности, полученного методом полного перебора, или оценкой этого результата для примеров большой размерности.

В предложенном алгоритме планирование полиномиальной сложности снимает ограничения на одновременное поступление на обработку задач, учитывает их информационную важность и минимизирует необходимое количество вычислительных модулей. Алгоритм обеспечивает минимальное число задействованных процессоров при обработке задач за счет их максимальной загрузки, что снижает энергопотребление вычислительного процесса. Применение предложенного алгоритма позволяет организовать вычислительный процесс с предоставлением вычислительных ресурсов сервера «по запросу» клиента в мобильной вычислительной сети.