Алгоритм поиска гармонии для улучшения подхода к задаче планирования потока перестановок в цехе

DOI:

Permutation flow-shop scheduling problem is another classical problem in scheduling that deals with the problem of sorting out the jobs through a sequence of operations to be undertaken on a number of machines to give the required amount of makespan, or other performance measures [1]. The distributed permutation flow-shop scheduling problem goes a step further by integrating this into multiple factories which have the same machinery and aims to reduce the makespan at the factory with the longest processing time [2]. This paper [3], addresses the problem using Constraint Programming while depending on sophisticated schedulers like interval variables and non-overlap constraints together with a new heuristic specifically used in computing lower bounds. Schedule management controls one of the key factors that determine system performance, it is, therefore, an important area of studies in operations management and industrial engineering. Flow-shop scheduling problems are part of multi-resource, multioperation scheduling problems [4]. In all the real-life industrial and logistical usages of using the proposed method, the time taken to identify an optimal solution influences both efficiency and costs [5], [12].

However, the problem discussed above becomes much more complicated as the total number of jobs, machines, and processing steps rises steadily, and these functions grow exponentially [6]. In addition, other attribute such as parallel machines and precedence constraints put more challenge on the optimality [7]. This paper covers on the Flow Shop Scheduling Problem (FSSP), an expansion of the Permutation Flow-Shop that is solved using HSA and is highly related to the Job-Shop Scheduling Problem (JSP). JSP is a typical example of the combinatorial optimization problem in the field of production planning and Scheduling. This model serves as a model for a scheduling situation in manufacturing or service environment, where a fixed number of jobs which are equal to a list of tasks or operations are due to be competed on a certain set of machines. Every task has a standard processing time or throughput and should be accomplished in a particular equipment.

Problem Definition

Permutation flow-shop scheduling problem (PFSP) can be defined as an optimization problem of scheduling jobs in a series of machines where every job passes through all the machines in a particular sequence. The objective is generally to maximize some performance criterion such as: minimum makespan (maximum throughput time to complete all jobs), minimum total throughput time or minimum idle time. Problem Definition to PFSP:

• •    There are n jobs (J₁,J 2 , ■ ■■,J_m) and m machines (M 1 ,M 2 , ..,M_m).

• •    Each J i has process for one machine in predetermine order.

• •    A given machine can handle only one job at a time while a given job can be on only one machine at a given time.

• •    The order in which the jobs are executed on any one machine greatly determines the total time taken and the degree of completion.

Constraints of PFSP include:

Each job J i must follow a predetermined order of machines (M 1 ,M₂,... ,M_m ) without reordering.

• •    If C ij represent the completion time of job J i on machine M j , then:

^Cij — ( ^Ci(j-1) + ^pij ) ^for J = 2, . , ^m

C i(j—1) is completion time of job J i on machine M j .

P ij is processing time of job J i on machine M j

• •    If C ij is completion time ofjob J i on machine M j , the sequence ofjobs that process jobs through machines to minimize C_max (makespan), where:

Cij= max (Ci(j-i), Cj(i—i) + pij), where:

C i(j—1) : represent to processing time ofjob J i on previous machine M j-1 .

C (i—1)j : represent to completion time of previous job J i-1 on machine M j .

P ij : represent to process time ofjob J i on machine M j .

The objectives of PFSP include:

• •    Minimize Makespan C_max : The time at which the last job ends or completes in the queue for processing.

Cmax = min max Ci where Ci is the time for completing the particular job i.

• •    Minimize Total Flow Time: Total completion time of all the jobs.

  Total Flaw Time

  
  

  -1

  
  

  n

  
  

  i=i

  
  

  C i

  
  

• •    Minimize Maximum Lateness: The time difference between the start of a job and the latest possible time to begin that job.

Literature Review

As for the problem addressed in [8], this paper employs Constraint Programming to solve the problem by using such sophisticated scheduling features as interval variables and nonoverlap constraints, along with new heuristics for lower-bound estimation. Two Constraint Programming models are introduced: FSPs that can address the Distributed Permutation Flowshop Scheduling problem as described previously and FSPs that can address the problem while allowing for the possibility that jobs can be processed in a different order on different machines within each factory.

The work presented in [9] is devoted to the Distributed Permutation Flowshop Scheduling Problem (DPFSP) with the objective of minimizing total tardiness. We propose a mixed-integer linear programming (MILP) model and develop two heuristic methods: a new discrete Harris Hawks optimization and an improve iterated greedy algorithm for this problem. Based on problem-specific knowledge, the proposed algorithms are complemented by superior methods, including path relinking and random sub-sequence/ single-point local search. In [10], this paper present introduce an efficient search method for solving the Permutation Flow shop Scheduling Problem (PFSP) based on the critical path concept and supported by three theorems. First, to suit the specific characteristics of the PFSP the critical path and the key points are identified. Based on these foundations, three theorems are proposed and demonstrated. Based on these theorems, a new neighborhood search method for the PFSP is established. During each iteration in the neighborhood search, only the first and the last job in the sequence, as well as the first job of every machine in the critical path, are computed. For any such problem, this strategy allows one to find the optimal neighbourhood solution employing a greatest of \(2m + 2\) searches at the most – where ‘m’ stands for machines. In [11], this paper considers the three-stage assembly flow shop scheduling problem of a production system with a fixed MP that is scheduled on one of the machines in the first stage. The objective of this scheduling problem is to reduce the makespan. The start times and durations of an MP are fixed, and during this time the affected machine is unable to Any job not completed before an MP must begin is treated as a non-restart type of MP wherein the job must start all over again once the machine is released again rather than continuing where it left off.

METHODOLOGY

Because there is practical applicability of flow shop scheduling problem, the Harmony Search algorithms are used for solving different sort of flow shop problems and having different objectives. Flow shop scheduling problems have been effectively modelled and solution by many researchers using Harmony Search [1]. For instance, a distributed hybrid flow shop problem was solved using a cooperative coevolution algorithm that was in turn based on the Harmony Search algorithm for the purposes of the analysis and further explorative and exploitative steps [2]. Furthermore, in energy-aware distributed flow shop scheduling processes, the use of Harmony Search-based optimization has appeared. The so called Hyper heuristics that apply other metaheuristic strategies such as Harmony Search for the purpose of optimization are also common [3]. Recent work used hyperheuristics for the blocking flow shop scheduling for multi-objective [4].

In this paper, utilizing Harmony Search Algorithm (HAS) to solve Permutation flowshop scheduling problem (PFSP). HSA is a metaheuristic technique that mimics from the improvisation process of musicians. This knowledge is essential in determining the bounds of the search space. The first step is initialized population size of solution, which represent values to begin of build solution. The second step applies the HSA by adjustment parameter of this algorithm. The parameters of this algorithm including harmony memory size, the objective function, the boundaries of the defined search space (min and max), harmony memory considering rate (hmcr), pitch adjustment rate (par), bandwidth (bw), and the length of The HSA seeks to build harmonies by iteratively this process to get best optimized dataset. Third step is evaluate objective function of each population. The output determines the fitness of every values. Finally, repeated this process until find good solution. The following algorithm (1) that show main step of HSA.

Algorithm : Harmony Search algorithm (HAS)

Input: Benchmark value (PFSP)

Output: Minimize Makespan

Step 1: Initialization population size of HSA

Step 2: Adjustment parameters HSA

Step 3: Evaluation Objective Function

Step 4: Iterative Optimization process until get near optimal solution

Harmony Search algorithm for PFSP used several hyper parameters as the following table (1).

Table 1. Hyper parameters in HSA.

Таблица 1. Гиперпараметры в HSA.

N	lb	Ub	dimension	iteration	par	hmcr	bw
10	Min	Max	16	10	0.5	0.3	0.2

RESULTS AND DISCUSSION

In this work, the benchmark set used is the ones provided for the Distributed Permutation Flowshop Scheduling Problem (DPFSP), which is publicly available. The first dataset is much smaller and it contains 420 records where for each unique (n= {4,6,8,10,12,16}, m={2,3,4,5}, F={2,3,4}) one uses five records as input.e initially introduced in [1] and are split into two datasets: a smaller and a larger set. The smaller dataset includes 420 instances, with five instances created for each combination of n = {4,6,8,10,12,16}, n is number of jobs, m = {2,3,4,5}, m is number of machines), and F={2,3,4}, number of factories). Rather, the larger data set includes 720 cases. These were obtained by extending the benchmark instances of Tailard [4] where six modifications of the number of factories are considered: the set F = {2,3,4,5,6,7}.More particularly, the data used in this research has a total of 540 records with 10 records each for F={2,3,4,5,6,7} × n={20,50,100} × m={5,10,20}, and an extra 120 records for F={2,3,4,5,6,7} × n={200} × m={10,20} and 60er and a larger set. The smaller dataset includes 420 instances, with five instances created for each combination of n = {4,6,8,10,12,16}, n is number of jobs, m = {2,3,4,5}, m is number of machines), and F= {2,3,4}, number of factories). On the other hand, the larger dataset comprises 720 instances. These were generated by expanding on Tailard’s classic benchmark instances [4], incorporating six variations for the number of factories, F= {2,3,4,5,6,7}. Specifically, this dataset includes 540 instances with 10 instances for each configuration of F={2,3,4,5,6,7} × n = {20, 50, 100} × m = {5, 10, 20}, an additional 120 instances for F={2,3,4,5,6,7} × n = {200} × m = {10, 20}, and 60 instances for F={2,3,4,5,6,7} × n = {500} × m = {20}. Table (2) showing the benchmark dataset include large and small dataset.

Table 2. Summarizing the benchmark.

Таблица 2. Подведение итогов сравнительного анализа.

Dataset	Number of Instances	Number of Jobs (n)	Number of Machines (m)	Number of Factories (F)	Instance Count per Configuration
Small	420	{2,4,6,8,10,1	{1, 2,3,4 }	{2,4, 6}	10
Large	720	{20,50,100,20	{10,15,20}	{1,2,3,4,5,6}	15
		0,500}

After applied HSA to PFSP Record the optimal job sequence and makespan for each benchmark instance as showing in table (3).

Table 3. The optimal task sequence and execution interval for each benchmark instance.

Таблица 3. Оптимальная последовательность задач и интервал выполнения для

			каждого экземпляра эталонного			теста.
Dataset	Jobs	Machines     Factories		Instance	HMS	Makespan	Best Job	Iterations
	(n)	(m)	(F)			(Optimal)	Sequence
Small	4	2	2	1	10	65	[1,3,4,2]	500
Small	6	3	3	1	15	110	[4,2,1,6,3,5]	1000
Small	10	4	2	3	10	190	[2,8,1,5,4,9,	1500
							10,3,6,7]
Large	20	5	5	1	20	325	[7,15,3,12,1	2000
							8,1,10,6,20,
							…]
Large	50	10	6	2	25	540	[33,10,25,1,	2500
							49,18,6,27,
							…]
Large	100	20	7	5	30	910	[54,21,10,98 ,5,42,31,67, …]	3000

This table provides a structured way to present the results of applying HSA to each instance, enabling comparison across different configurations and sizes in the benchmark. The actual makespan and job sequences will vary depending on the specific instance and HSA parameters. The following figures showing the iterations of process dataset and number of jobs.

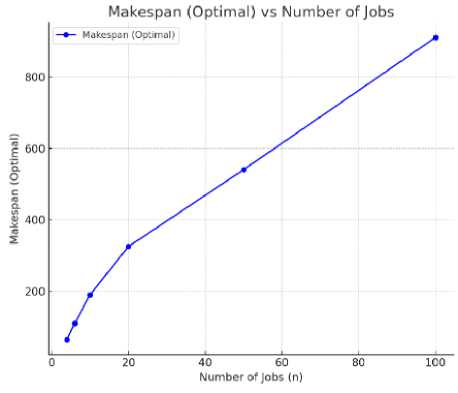
Figure 1. Number of Jobs.

Iterations per Dataset

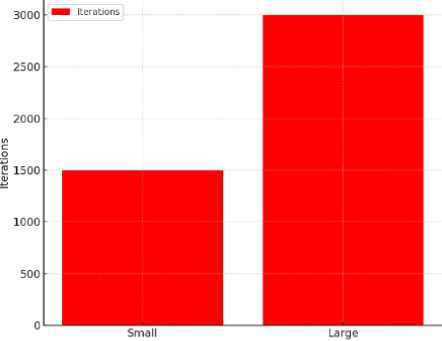
Dataset

Figure 2. Number of iterations.

Рисунок 1. Количество рабочих мест.

Рисунок 2. Количество итераций.

The Optimal schedule according to the PFSP model for the problem instance showing in Figure (3):

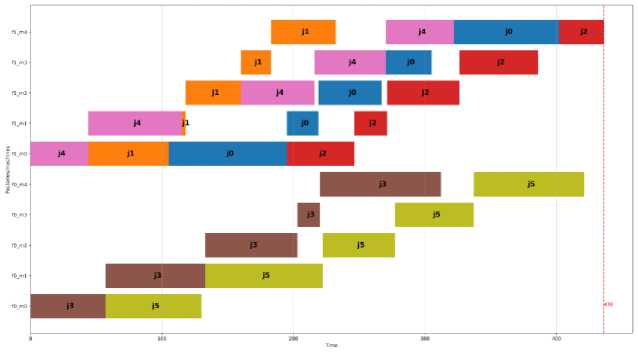
Figure 3. The Optimal schedule.

Рисунок 3. Оптимальный график.

Figure 4 shows the key idea of determining lower bounds of influence measures where the parameter k is determined by formula [2]. At the left of the figure it presents where i is the beginning or the first machine; at the right side of the figure, it presents where i is the last or the end machine and in the middle of the figure, it presents where i can be in between machines.

Makespan Lower Bounds Considering Execution Without Gaps at Each Machine

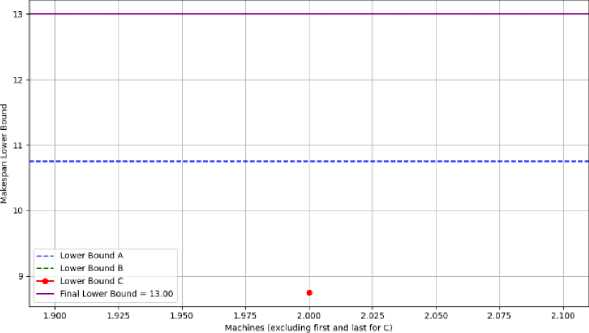
Figure 4. Lower bounds of Makespan taking into considerations the possibility of executing all the jobs in a continuous manner at each of the machines.

Рисунок 4. Нижние границы периода производства с учетом возможности выполнения всех работ непрерывно на каждом из станков.

In figure (5) the ‘distance of lower bounds to the best-known values” of the problem instances, the factories, jobs and the machine have been provided. The horizontal axis corresponds to the problem instances as determined by the combination of the three factors: This map has the horizontal axis representing the number of factories, the number of jobs and the number of machines while the vertical axis represents the distance values which as noted exhibit oscillatory features.

Wave of Distance from Lower Bounds to Best-Known Values

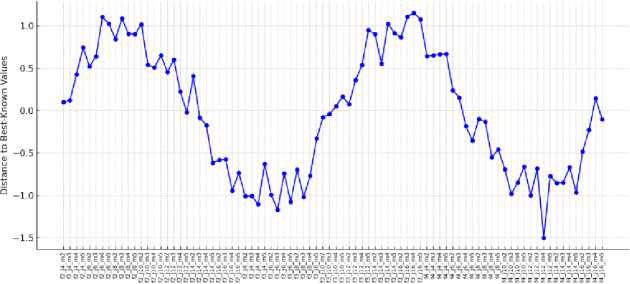
Problem Instances

Figure 5. How good they are, can be estimated by measuring the distance of lower bounds to the best-known values for instances of the small dataset.

Рисунок 5. Насколько они хороши, можно оценить, измерив расстояние нижних границ до наиболее известных значений для экземпляров небольшого набора данных.

While finding the lower bound for the set of the problem instances contained in the large dataset, some of the specific cases similar to I-2-16-2-5 have been identified where the calculated lower bound with the help of Health and Social Care Analytics tools is same as the

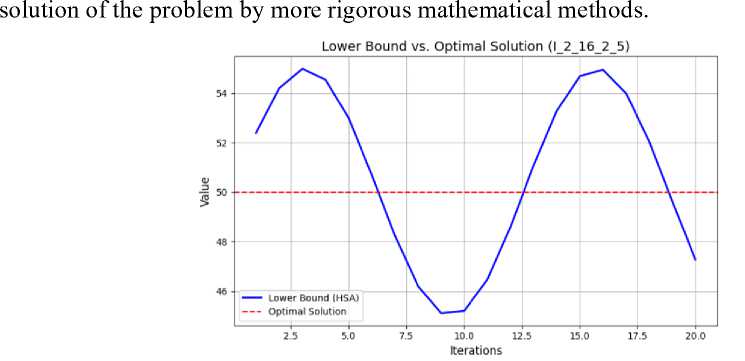
Figure 6. Distance of lower bounds to the best-known values for instances of the “large” dataset.

Рисунок 6. Расстояние нижних границ до наиболее известных значений для экземпляров «большого» набора данных.

On comparing the two figures 5 and 6, it can also be observed that with every increase in the number of factories the percentage difference is having an upward tendency. Furthermore, for both the small and large datasets, within problem instances that have the same number of factories using, the percentage differences tend to reduce as the number of jobs and machines increase using harmony search algorithms (HSA).

CONCLUSION

The result revealed that the proposed HSA yielded a higher level of effectiveness in solving the DPF-SF problem by achieving enhanced makespan compared to the other arrangements. Constraint programming techniques, interval variables and non-overlap constraints provided a good solution to technical scheduling problems. While optimising the approach of the HSA search, the heuristic for computing lower bounding provided a clue to enhance solution quality. The experimental results given for the algorithm was tested on small set and large set, showing its suitability for large problem instances. As observed from outcomes, it was shown that HSA effectively prevented percentage deviation on makespan from escalating when the number of jobs and machines in the system was increased. This paper validates that HSA is indeed a usable technique for improving the PFSP and DPFSP models that could be used in future realistic industrial scheduling applications.